WIGWAM水下核爆炸气泡脉动理论计算及数值模拟对比分析

刘哲函,王晓明,王 燕,李 健,南 德,刘泽玉,曾 志

(1. 清华大学 工程物理系,北京 100084;2. 禁核试北京国家数据中心,北京 100085)

1963年,美国、英国和苏联在莫斯科达成《部分禁止核试验条约》(Partial Test Ban Treaty,PTBT),禁止在大气层、外层空间和水下进行核试验。在此之前,水下核试验一共进行了8次(美国5次,苏联3次)。其中,美国于1955年5月14日进行的WIGWAM水下核试验是迄今为止爆炸深度最深、当量最大的水下核试验,爆炸地点位于西经126.27°、北纬28.73°,太平洋东部,距离加利福尼亚西海岸约800 km,爆炸深度为610 m,爆炸当量为30 kt TNT。尽管WIGWAM水下核试验距今已近70年,但关于试验测量的公开信息很少。

水下爆炸的研究一般以理论分析、实验研究及数值模拟等方式开展。理论分析通过对复杂问题进行简化,得到的是近似结果;实验研究通过对测试数据的分析得到半经验半理论的公式,但难以解释现象的本质,且实验具有限制性,如大当量的爆炸不易具备实现条件及测量参数不完备等;数值模拟可较好地结合理论分析和实验研究的优势,具有成本低、重复性好及测量参数丰富等优点,随着计算机计算能力的不断提高,水下爆炸的数值模拟技术越来越受重视。

气泡脉动是水下爆炸后形成气泡的膨胀和压缩周期性运动,是水下爆炸所特有的现象,能作为识别水下爆炸的特征判据,但利用气泡脉动区分水下核爆炸和常规爆炸的研究还未见报道。

为区分水下核爆炸和常规爆炸,本文从水下爆炸气泡脉动的理论计算和数值模拟入手,根据相关文献中提及的美国WIGWAM试验的有限信息,开展了水下核爆炸气泡脉动参数的理论计算,应用AUTODYN数值模拟软件和等效缩比方法仿真了同等当量条件下水下常规爆炸(以TNT为例)的气泡脉动过程,并对两者的气泡脉动结果进行了对比分析,提出了一种可用于区分水下核爆炸和常规爆炸的方法。

1 水下爆炸气泡脉动参数的理论计算

在理想条件下,忽略水面和水底反射的影响,水介质由于具有较低的可压缩性,可视为不可压。在此条件下,爆炸形成的气泡推动气泡周围的水体向外做径向运动,运动过程中的能量守恒方程可表示为[1]

(1)

其中:R为气泡半径;ρ为水的密度;p为气泡在水下所处位置的压强;E(R)为气泡的内能;Y为爆炸后气泡脉动的总能量。式(1)左边第一项为周围流体的内能,第二项为气泡膨胀至R的过程中对静水压力所做的功。

当气泡膨胀至最大半径Rmax时,常规爆炸的气体内能E(R)相对气泡脉动做功可忽略,且dR/dt=0,式(1)可简化为

(2)

压强p可表示为

p=ph+p0=ρg(h+h0)

(3)

其中:ph为水下深度h处的水压;p0为标准大气压;ρ为水的密度,103kg·m-3;g为重力加速度,9.8 m·s-2;h0为标准大气压的等效水深,10.34 m。

爆炸后气泡脉动的总能量可表示为

Y=η1×W×Q

(4)

其中:η1为第一次气泡脉动能量占爆炸总能量的比例;W为炸药质量,kg;Q为炸药的热质比,TNT炸药的热质比一般取为4.18×106J·kg-1。由式(4)可得水下TNT爆炸的第一次气泡脉动的最大半径,表示为

(5)

将式(5)代入式(1)可得

(6)

由式(6)可得

(7)

即

(8)

两边积分后第一次气泡脉动周期T可表示为

(9)

将式(3)及式(5)代入式(9)可得

(10)

定义ηn(n≥2)为第n次气泡脉动与前一次气泡脉动能量的比,则由式(5)和式(10)可递推得到第n次气泡脉动的最大半径Rmax, n和周期Tn,表示为

(11)

(12)

由式(12)可知,气泡脉动周期与当量和爆炸深度有关,还与不同爆炸场景的气泡脉动能量传递比例有关。

由式(11)和式(12)可知,Rmax, n和Tn比可消除ηn和W,由此可得到第n次气泡脉动深度hn,表示为

(13)

在水下爆炸探测中,通过探测设备可获取的信息主要是冲击波的到达时间及气泡脉动的周期Tn,由气泡脉动周期Tn可估计水下爆炸的深度hn和当量[2]。根据水下爆炸深度、当量及气泡脉动周期的结果,由式(10)可得到第一次气泡脉动能量占爆炸总能量的比例η1,表示为

(14)

由式(12)递推可得到ηn,表示为

(15)

2 水下爆炸数值模拟理论及应用

2.1 数值模拟理论及仿真软件

数值模拟需建立可反映物理变化规律的数学模型,一般以微分方程作为控制方程进行物理过程的描述,以初始条件和边界条件作为确定的物理变量的表达。控制方程的描述主要有欧拉方法和拉格朗日方法[3],在计算机实现中一般通过网格进行数值计算。拉格朗日方法是基于物质坐标,计算网格随材料的变形和运动而变化,在不同单元间传递动量和能量,具有物质点的场变量变化易追踪、边界条件易表达等优点,但难以解决网格畸变带来数值计算精度下降的问题[4]。欧拉方法是基于空间坐标,网格单元不随时间变化,物质在网格间进行质量、动量和能量等场变量的传递,在物质变形中网格的体积和形状保持不变,避免了网格畸变带来的问题。因此,在固体力学研究领域中主要采用拉格朗日方法,代表性的是有限元法(finite element method,FEM);在水下爆炸等流体力学研究领域主要采用欧拉方法,代表性的是有限差分法(finite difference method,FDM)[5]

水下爆炸仿真领域较成熟的商业软件主要有LS-DYNA、DYTRAN、ABAQUS和AUTODYN等[6],其中,AUTODYN在近场爆炸模拟中采用高阶多物质欧拉求解器模拟水下爆炸冲击波的形成和传播,模拟计算结果与实验数据接近;在远场水下爆炸问题中将3维计算问题的初始阶段在1维模型中进行模拟,有效减小了计算量;在气泡脉动模拟方面,利用多物质欧拉求解器能较好地模拟气泡脉动过程[7]。AUTODYN在水下爆炸模拟方面功能最全面,优势明显,可较好地模拟近场、远场爆炸和气泡脉动过程,所以选择AUTODYN作为数值模拟工具开展水下爆炸模拟方法研究。

2.2 AUTODYN在水下爆炸仿真中的应用

水下爆炸的数值模拟包括爆轰、冲击波的产生和传播、气泡的形成和脉动及水下爆炸能量输出等过程,爆轰过程的数值模拟通常采用引入人工黏性系数等技术对爆轰过程中的强间断面进行光滑处理,以状态的连续变化代替状态的间断变化,在不影响数值计算的同时满足计算程序实现的要求[8]。冲击波和气泡脉动的数值模拟可通过对冲击波阵面和气泡表面之间流体不定常运动求解,假设水为等熵无黏流体的条件下,通过初始条件和边界条件参数求解爆炸流场的参数[9]。AUTODYN软件中关键参数及求解条件的设置对水下爆炸数值模拟的结果至关重要。

2.2.1 爆轰状态方程及参数设置

常规爆炸中,炸药爆轰在微秒量级的时间内将炸药转换成具有高压、高温的气态产物,同时释放出大量的热。在忽略热传导和黏性影响的条件下,爆轰过程可由不定常的理想流体动力学方程表示。与一般的流体力学计算不同,方程组的求解需引入化学反应进程变量,使化学反应与流体力学运动相耦合。

对于高能炸药(以TNT为例)的爆轰产物一般采用JWL(Jones-Wilkins-Lee)状态方程进行计算,JWL状态方程参数可通过实验方法确定,表示为[10]

(16)

其中:pJWL为爆炸产生的压强;A,B,R1,R2,ω为常数;V为相对体积;E0为比热容力学能。状态方程中各项依次反映了高压区、中压区和低压区的状态。

在AUTODYN软件中,TNT炸药爆轰产物的JWL状态方程的参数如表1所列。

表1 TNT炸药的JWL状态方程模型参数Tab.1 Parameters of JWL equation of state model for TNT

2.2.2 水的状态方程及爆深模拟

凝聚介质状态方程对于水的状态有多项式状态方程和冲击波状态方程2种形式。其中,冲击波状态方程利用冲击波的特性对凝聚介质状态方程进行联立,并利用冲击波速度的实验关系式代入求解,多项式状态方程是凝聚介质状态方程的通式,对流体在不同状态的表达形式不同[11-12]。

当水压缩时(μ>0),状态方程可表示为

p=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0E

(17)

当水膨胀时(μ<0),状态方程可表示为

p=T1μ+T2μ2+B0ρ0E

(18)

当水既不压缩也不膨胀时(μ=0),可简化为

p=B0ρ0E

(19)

其中:μ=ρ/ρ0-1,为水的压缩比;ρ为水压缩或膨胀后的密度;ρ0为水的初始密度;A1,A2,A3,T1,T2,B0,B1为常数,分别取值为2.2,9.54,14.57,2.2,0,0.28,0.28 GPa;E为静水内能。

在水下爆炸气泡脉动的数值模拟中,可通过设置静水压强来模拟水下爆炸的深度。AUTODYN软件对水下爆炸的爆深模拟中,利用静水内能等效静水压强,实现不同深度的模拟。将水视作既不压缩也不膨胀的介质时,水下爆炸深度h处水的静水内能E可表示为

(20)

根据上文中B0,g和h0的取值,则有

E=35×(h+10.34)

(21)

2.2.3 边界条件设置

在AUTODYN软件中,常用的边界条件有透射边界(transmitting boundaries)、流出边界(flow out)和刚性边界(none)3种。在气泡脉动的数值模拟中,如有限元模型太小,透射边界条件会使冲击波在边界处压力迅速衰减,导致脉动周期过大;流出边界条件会使冲击波在边界处发生反射,引起水域内部压力增大,导致脉动周期偏小;刚性边界条件会使冲击波在边界处完全反射,引起水域内部压力过大,导致脉动周期过小[13]。为减小边界条件的影响,建立有限元模型时须适当扩大区域,可采用在关注区域使用较小网格,其他区域使用过渡网格的方式。一般情况下,边界条件选取流出边界类型。

2.2.4 人工黏性条件设置

通过在计算程序中引入人工黏性条件,可解决冲击波物理量的突变带来的微分方程不连续问题,人工黏性系数q可表示为

(22)

其中:ρm为材料密度;CL为人工黏性一次项系数;CQ为人工黏性二次项系数;l为材料的特征长度;C为材料中的波速;ε为体积变化率。

人工黏性的一次项系数是减弱高阶频率中的振荡,二次项系数是引入阻抗压力防止压溃。人工黏性系数的引入会在计算域中的几个网格内光滑冲击波阵面,抑制陡峭峰值后压力的振荡,但同时会影响峰值压力的大小。过高的人工黏性系数会增加仿真结果与真实值的偏差,过低的人工黏性系数则难以削弱冲击波后的伪振荡[14]。

相关仿真实验的结果表明[15],人工黏性的二次项系数对仿真结果的影响较小,建议取值范围为0.8～1;一次项系数对仿真结果中冲击波峰值压力的影响较大,取值范围为0.005～0.04时,可满足不同当量条件下近远场仿真的精度要求。

2.2.5 计算网格的设置

水下爆炸数值模拟的总偏差主要由舍入偏差和截断偏差组成,舍入偏差是计算过程中浮点数的四舍五入引入的偏差,截断偏差是微分方程离散为差分方程时引入的偏差。随着网格点数的增加,截断偏差会减小,舍入偏差会增加,但舍入偏差比截断偏差的影响要小得多,因此,网格越小越能保证计算的精度,但同时还需考虑计算时间和计算资源的耗费。此外,还可采用过渡网格的方式,将关注区域的网格变小,其他区域采用大尺寸网格,可在保证计算精度的前提下节约计算时间。张社荣等[16]对水下爆炸数值模拟网格尺寸的实验研究认为,当网格尺寸小于炸药半径的1/3时,计算精度可满足工程要求。

2.3 基于等效缩比方法的水下大当量爆炸数值模拟

使用AUTODYN软件模拟千吨级TNT当量水下爆炸时,网格尺寸设置大会导致计算偏差过大而停止计算,网格尺寸小时则带来了计算资源和计算时间无法承受的问题,因此考虑采用缩比的方法来模拟水下千吨级TNT爆炸的过程。

Hopkinson等提出了爆炸的等效缩比定律,认为相同形状但大小不同的炸药在等比距离上产生相似的爆炸,该定律称为霍普金森-克兰兹定律(Hopkinson-Cranz Scaling Law),也称为立方根比例定律(Cube-root Scaling Law)[17]。

由等效缩比定律引入尺度因子λ,在水下爆炸的缩比模型中主要物理量如表2所列。

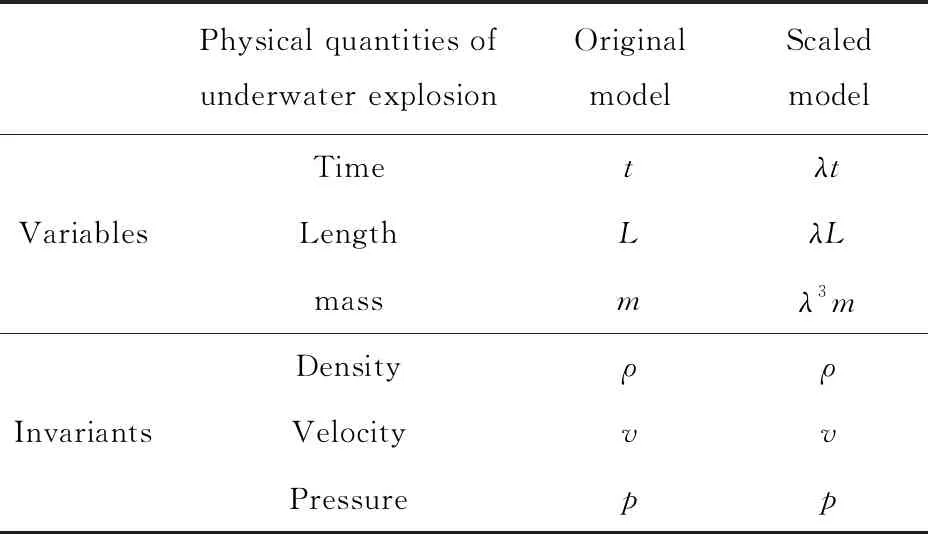
表2 水下爆炸等效缩比模型中主要物理量Tab.2 The main physical quantities in the equivalent scaled model of underwater explosion

考虑到WIGWAM试验30 kt TNT当量的量级,将尺度因子λ设置为10-3。在此条件下,质量单位由kt缩比为g,长度单位由m缩比为mm,时间单位由s缩比为ms。AUTODYN软件中通过静水压强模拟水深,压强在缩比模型中为不变量,缩比仿真WIGWAM试验等效TNT当量和爆炸深度时的主要参数设置为

(1) 由于爆轰状态方程和水的状态方程中的参数均为缩比模型中的不变量,因此,材料属性设置采用默认值。

(2) 在爆炸深度的模拟中,选择多项式状态方程通过设置静水内能实现爆炸深度的模拟,将爆炸深度610 m代入式(21),计算得到的静水内能数值为21 712。

(3) 为更好地仿真气泡脉动半径变化过程,边界条件选取为流出边界类型。

(4) 人工黏性的一次项、二次项系数设置为0.04和0.9。

(5) 计算30 g TNT球形装药的半径为16.4 mm,按照网格尺寸小于炸药半径1/3的计算精度要求,网格尺寸设置应小于5.5 mm。在兼顾计算精度及效率的情况下,将10 m水域划分为5 000个网格,即网格尺寸设置为2 mm;为更精确地模拟炸药附近1 m范围内的爆炸效应,将距离炸药中心点1 m范围内的水域采用过渡网格尺寸,为1 mm。

3 WIGWAM水下核爆炸理论计算与数值模

拟结果

3.1 WIGWAM水下核爆炸理论计算结果

美国加州大学伯克利分校的Pritchett等[18]提到WIGWAM试验中观测到的3次气泡脉动时间分别为2.88,5.5,7.3 s,由此可得3次气泡脉动的周期分别为2.88,2.62,1.8 s;通过半经验半理论公式估计各次气泡脉动周期结束时(气泡由于浮力而上升,此时气泡所处深度为本周期内深度最小值,下一脉动周期内深度最大值)的深度分别为527,377,275 m,取各次气泡脉动周期内的深度最大值作为气泡脉动深度计算气泡脉动的能量,即第一次、第二次和第三次气泡脉动深度h1、h2、h3分别取为610,527,377 m。

将上述数据代入式(14)和式(15)中可得到第一次气泡脉动能量占爆炸总能量的比例η1为0.37,第二次气泡脉动能量占第一次气泡脉动能量的比例η2为0.53,第三次气泡脉动能量占第二次气泡脉动能量的比例η3为0.14。

WIGWAM试验的当量为30 kt TNT,即W=3×107kg,将W,ηn,hn代入式(11)计算得到第一次、第二次和第三次气泡脉动的最大半径,分别为122,104,60 m。

3.2 基于等效缩比方法的等效TNT当量水下爆炸

数值模拟结果

根据第2.3节的数值模拟参数,使用AUTODYN软件仿真模拟30 g TNT球形装药在水下610 m深度处爆炸,得到等效缩比模型TNT爆炸数值仿真结果,如图1所示。

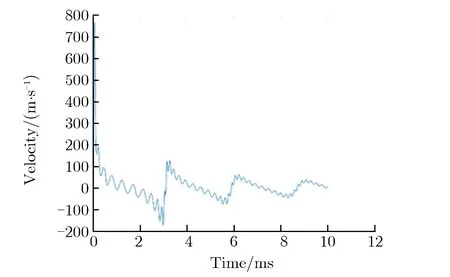
(a) Particle velocity of bubble pulsation vs. time

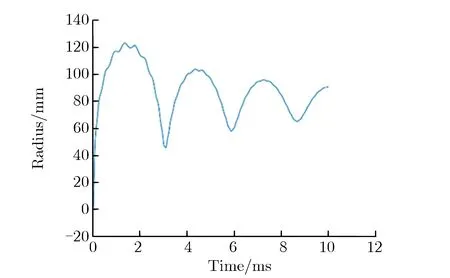
(b) Radius of bubble pulsation vs. time图1 等效缩比模型爆炸数值仿真结果Fig.1 Numerical simulation results of equivalent scaled model for explosion

由图1(a)可见,速度过零点时为气泡脉动周期内的最大半径和最小半径时刻;由图1(b)可见,各次气泡脉动的最大半径呈逐次减小的趋势。

提取气泡半径数据中的相关数值,得到第一次脉动的周期为3.10 ms,气泡最大半径为123 mm;第二次气泡脉动的周期为2.78 ms,气泡最大半径为104 mm;第三次气泡脉动的周期为2.80 ms,气泡最大半径为96 mm。由等效缩比模型还原到30 kt TNT的爆炸场景时,气泡脉动周期的单位由ms转换为s,气泡半径的单位由mm转换为m。

将换算单位后的周期及半径数值代入式(13)计算得到第二次、第三次气泡脉动深度分别为473 m和396 m,第一次气泡脉动深度取等效TNT爆炸数值模拟时的爆炸深度为610 m。

将仿真模拟得到的气泡脉动周期和深度估计值及代入式(14)和公式(15)中,可得到第一次气泡脉动能量占爆炸总能量的比例η1为0.46,第二次气泡脉动能量占第一次气泡脉动能量的比例η2为0.39,第三次气泡脉动能量占第二次气泡脉动能量的比例η3为0.66。

4 水下核爆炸与常规爆炸对比分析

4.1 水下核爆炸与常规爆炸的理论差异

水下核爆炸与常规爆炸(以TNT为例)的区别主要在于:

(1) 反应时间上存在微小差异。核爆炸的反应时间在纳秒量级,而常规爆炸的反应时间一般为微秒量级,但这种时间上的差异在爆炸气体向外推动水体做功的过程中可忽略。

(2) 爆炸气体的温度存在明显差异。核爆炸的温度一般在几千万开,而常规爆炸的温度一般在几千开,因此爆炸后形成的气泡中的气体内能不同。

(3) 爆炸气体的成分不同。常规爆炸气体的主要成分是CO和N2,核爆炸除常规爆炸的气体外,还有大量的金属气体,气体内能下降比常规爆炸快,且气体处于不均匀状态,气泡中心的气体温度比外围要高得多。

4.2 气泡脉动理论计算及数值模拟结果对比分析

对比WIGWAM试验的理论计算结果及等效TNT当量水下爆炸的数值模拟结果,气泡脉动计算结果对比如表3所列。由表3可知,等效TNT爆炸数值模拟得到的第一次、第二次气泡脉动的周期均略高于WIGWAM试验的观测结果,但第三次气泡脉动的周期显著大于WIGWAM试验的观测结果;等效TNT爆炸数值模拟得到的第一次、第二次气泡脉动的最大半径与WIGWAM试验的理论计算结果基本一致,但第三次气泡脉动的最大半径显著大于WIGWAM试验的理论计算结果。

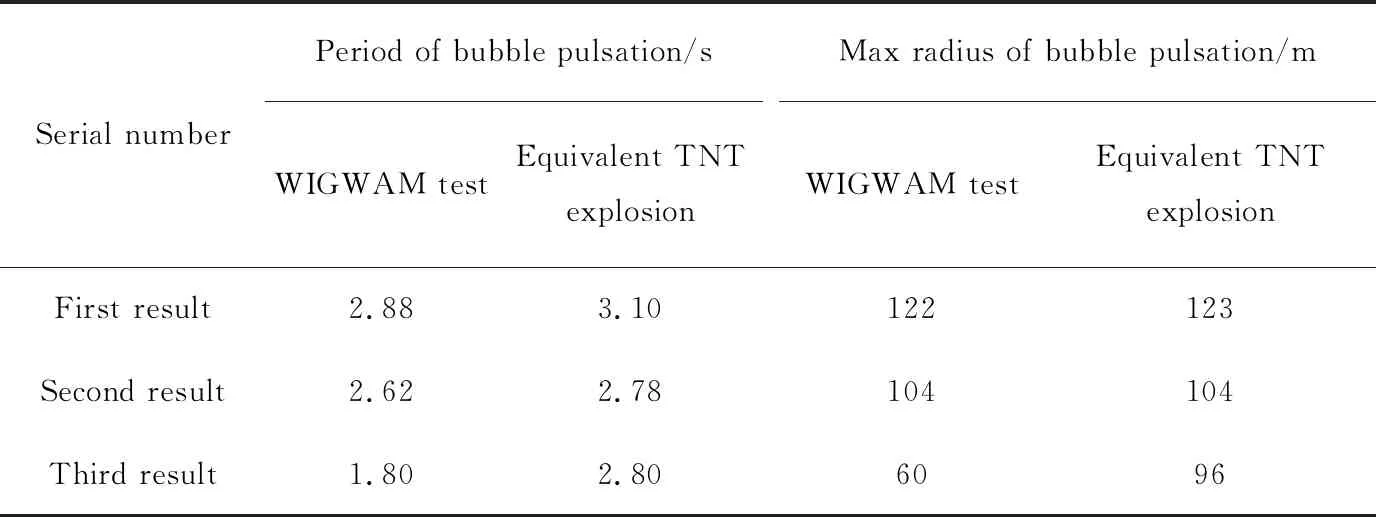
表3 气泡脉动计算结果对比Tab.3 Comparison of calculation results of bubble pulsations

对比分析WIGWAM试验计算结果及等效TNT爆炸数值模拟结果,气泡脉动能量比如表4所列。由表4可知:

表4 气泡脉动能量比值对比Tab.4 Comparison of energy ratios between bubble pulsations

(1) WIGWAM试验第一次气泡脉动能量占爆炸总能量的比例低于等效TNT爆炸的比例。由于相同爆炸能量产生的冲击波所扩散出去的能量比例一致,造成两者比例差异的原因是水下核爆炸产生的爆炸气体温度高达几千万开,等效TNT爆炸产生的爆炸气体温度只有几千开,而理想气体的内能与热力学温度成正比,水下核爆炸后留在气泡中的内能比等效TNT爆炸要高。

(2) WIGWAM试验第二次气泡脉动的能量占第一次气泡脉动能量的比例高于等效TNT爆炸的比例。这是由核爆炸留在第一次气泡中的内能转换成了气泡的脉动能量所引起的,在冲击波所扩散出去的能量占爆炸总能量比例一致的情况下,将水下核爆炸第一次气泡脉动能量与爆炸留在气泡中内能之和视作第一次气泡脉动能量,其占爆炸总能量的比例及两次脉动能量之间的比例与等效TNT爆炸一致,此时计算得到水下核爆炸第二次气泡脉动能量占第一次气泡脉动能量的比例为0.46×0.39/0.37=0.48,接近0.53,小于0.53的原因是内能转化为气泡脉动能量的效率比气泡脉动之间能量传递的效率要高,计算结果可在一定程度上验证水下核爆炸第二次气泡脉动能量占第一次气泡脉动能量比例比等效TNT爆炸高的结果。

(3) WIGWAM试验第三次气泡脉动的能量占第二次气泡脉动能量的比例远低于等效TNT爆炸的比例。这是因为水下核爆炸后留在气泡中的内能已基本在第二次脉动中转化,且与TNT爆炸产生的气体相比,核爆炸所产生的气体是不均匀的,中心温度比外围温度要高得多,气泡-水界面上的泰勒不稳定性效应会导致界面破裂使水滴进入气泡内部,引起核爆炸气泡内部金属气体的凝结,减小气泡内部压强,导致气泡脉动能量的急剧下降。

对比分析WIGWAM试验和等效TNT爆炸气泡脉动周期比,气泡脉动周期比计算结果对比如表5所列。

表5 气泡脉动周期比计算结果对比Tab.5 Comparison of periods between bubble pulsations

由表5可知:水下核爆炸第二次气泡脉动周期与第一次周期的比与等效TNT爆炸相差不大,水下核爆炸第三次气泡脉动周期与第二次周期的比远小于等效TNT爆炸。

综上,对比水下核爆炸(WIGWAM试验)和常规爆炸(TNT爆炸)的气泡脉动参数差异,水下核爆炸第三次气泡脉动在能量占比、最大半径和脉动周期都远小于常规爆炸,由于在水下爆炸探测数据的处理中可通过倒谱分析较好地提取气泡脉动周期信息,因此提出将第三次气泡脉动周期与第二次气泡脉动周期的比作为识别两类场景的依据。

此外,由式(12)可知,气泡脉动周期比不是由气泡脉动能量比例单因素决定的,还受爆炸深度的影响。基于气泡脉动周期比判据对水下核爆炸的判断要与同等深度同等当量的常规爆炸进行比较,已知爆炸深度和当量的水下常规爆炸气泡脉动周期比可通过数值模拟结果计算得到。

5 结论

水下核爆炸与常规爆炸对比研究的难点在于既缺乏水下核爆炸的实验数据,也缺乏同等规模常规爆炸(千吨量级TNT当量)的测量数据。本文围绕如何将水下核爆炸与常规爆炸理论上的差异反映到实际探测的物理参数中这一问题,选择从水下爆炸特有的气泡脉动现象展开研究,提出了基于气泡脉动周期比区分水下核爆炸和常规爆炸的方法。

根据WIGWAM水下核爆炸理论计算和等效TNT当量水下爆炸数值模拟结果的对比分析,认为同等当量条件下的水下核爆炸和TNT爆炸在第一次和第二次气泡脉动的周期和最大半径上没有显著区别,第三次气泡脉动的周期和最大半径则有明显的差异,可较好地区分水下核爆炸和TNT爆炸场景。需说明的是,WIGWAM水下核爆炸属于深水爆炸,在计算气泡脉动参数时不用考虑水体冲出水面的影响,而浅水核爆炸的场景则较为复杂,除考虑水体冲出水面的因素外,还需考虑水面和水底反射的影响,对于浅水核爆炸与常规爆炸如何区分还需进一步的研究。