初始信号对时间反演性能的影响分析

陆希成,田 锦,林荣刚,郭昕伟,胡 晓,邱 扬

(1. 西安电子科技大学 机电工程学院,西安 710071;2. 中国电子科技集团公司 第二十研究所,西安 710068;3. 西安新佳腾电子科技有限公司,西安 710061)

时间反演具有时空聚焦特性,在许多领域都有潜在的应用[1-2]。其中,在电磁学方面,基于标量和矢量衍射理论已证明电磁时间反演的时间压缩和空间聚焦特性[3-4]。时间压缩到初始信号的宽度,空间聚焦大小通常满足衍射理论。但在精细结构下,时间反演还会出现空间聚焦的超分辨率现象[5-7]。基于时间反演的这些特征,时间反演技术广泛应用于保密通信[8-10]、超分辨率成像[11-12]、脉冲压缩[13-14]、电磁兼容性测试[15]、微扰探测[16-17]及无线功率传输[18]等方面。在这些应用中,最常采用的一种时间反演系统由收发天线和腔体品质因子Q值较高的腔体,即时间反演腔(time reversal cavity,TRC)组成[19-20],具有良好的封闭性和较强的散射性,不但可提高时间反演过程中的多径效应,还克服了收发天线的时空覆盖限制,具有很好的反演性能[21]。对于这类TRC,人们还研究了腔体和天线的特征参数对时间反演性能的影响,如腔体结构、腔体损耗、模式数量、天线类型和位置等[22-26]。这些研究结果为时间反演腔和天线的选择及设计提供了依据。

对于初始信号对反演性能的影响,文献[27]中通过实验方法得到带宽越大反演性能越好的结论,并给出了经验公式,但仍缺乏对初始信号影响原因的深入分析。由此,本文基于时间反演信噪比(signal-to-noise raito, SNR)的定义,利用重构信号与初始信号的正交特性,深入分析初始信号的频率和脉冲宽度对TRC反演性能的影响,并给出基本规律,便于选择合适的初始信号来提高系统的反演性能。

1 TRC时间反演

TRC的时间反演过程一般可分成3步:第一步,获得系统的响应信号;第二步,将响应信号进行时间翻转,形成反演信号;第三步,将反演信号在接收位置输入到该系统,在初始位置产生反演重构信号。典型的时间反演过程如图1所示。当电磁波从一个端口经TRC传播到另一个端口时,形成了一条完整的传输信道。如该系统的(单位)冲激响应函数为h(t),则它的时间反演重构信号srec(t)可表示为

srec(t)=sori(t)h(t)h(-t)

(1)

其中,t和sori(t)分别为时间和初始信号。在频域情况下,时间反演Srec可表示为

Srec(ω)=Sori(ω)H(ω)H*(ω)

(2)

其中,ω和H(ω)分别为角频率和系统的传递函数;Sori(ω)为初始信号。由式(2)可知,反演重构信号与初始信号和系统响应特性密切相关。文献[25]给出了系统响应特性对时间反演性能的影响,本文将重点分析初始信号对时间反演性能的影响。

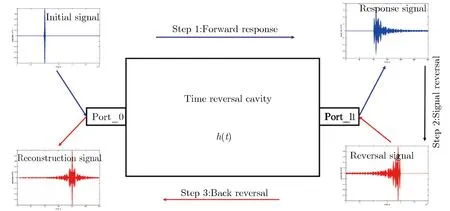
图1 典型的时间反演过程Fig.1 Typical time reversal process

2 反演性能分析

真实情况下,电磁波在TRC中的传播会出现串扰及损耗等现象,破坏了时间反演的对称性,导致反演重构信号与初始信号的波形并不完全一致[21,25],在反演重构信号中出现了时间主瓣和时间旁瓣(也称为噪声),典型的时间反演重构信号如图2所示。在这种情况下,反演重构信号可重新表示为[28]

srec(t)=ρsori(t)+n(t)

(3)

其中:n(t)为旁瓣噪声信号;ρ为主瓣与初始信号的比例系数。根据初始信号和重构信号的正交关系,可得到

(4)

其中:〈〉为正交映射运算符;f为激励频率;f2和f1分别为信号频谱的上下限。

图2 典型的时间反演重构信号Fig.2 Typical time reversal reconstruction signal

2.1 反演信噪比

通常情况,可将反演重构信号的主瓣最大值与噪声最大值的比值定义为反演信噪比,也称为峰值信噪比ηSNRp,表示为

(5)

根据时间反演的时空聚焦特征,重构信号的主瓣最大值通常出现在t=0时刻,即srec(0)。另外,对于噪声信号,如采用功率指数衰减近似表征它的衰减特征,最大值也近似位于t=0时刻附近。因此,当TRC的Q值很大时,可得噪声最大值,近似表示为

(6)

其中,εN为重构信号的噪声能量,可表示为

(7)

其中,εM为重构信号的主瓣能量,可表示为

(8)

在这种情况下,峰值信噪比可进一步表示为[28]

(9)

其中:εori为初始信号的能量;ηSNRε为重构信号的能量信噪比,即

(10)

由式(10)可知,ηSNRε也是描述时间反演性能的一个主要参数。

2.2 频率对峰值信噪比的影响

式(9)右边第一项括号内的表达式可写为τ=Q/(πf),即腔体的衰减时间常数。由此可知,信噪比与TRC的衰减时间常数密切相关。另外,衰减时间常数不但与腔体损耗有关,还与激励频率(初始信号频率)有关。其中,对于激励频率,如TRC电导率σ≫ωε(其中,ε为介电常数)时,衰减时间常数τ可表示为

(11)

其中:V为腔体体积;A为腔体表面积;μ和μr分别为磁导率和相对磁导率。由式(11)和式(9)可知,当TRC不变时,峰值信噪比随频率的增大而减小。

2.3 脉冲宽度对峰值信噪比的影响

对于脉冲信号,信号能量通常可表示为脉冲峰值与时间的乘积,即

(12)

其中:tpw为初始信号的脉冲宽度;k1为波形系数,大小与波形相关。由此式(9)右边第二项括号内的表达式可写为

(13)

由式(13)和式(9)可知,初始信号的脉冲宽度越窄,峰值信噪比越大。

另外,式(9)右边第三项也包含了初始信号的信息。为简化分析并不失一般性,可假设初始信号在频率范围[f1,f2]内是均匀分布的。由此,重构能量信噪比可进一步表示为

(14)

其中,Δf=f2-f1。由式(14)可知,能量信噪比不仅与传递函数有关,还与信号的带宽有关。在不考虑传递函数变化影响的情况下,表面上看,信号带宽越宽,则能量信噪比越大,即峰值信噪比越大。

另外,对于脉冲信号,通常信号带宽与脉冲宽度(或上升沿)成反比关系,即

(15)

其中,k2为比例系数,与具体的脉冲波形有关。由式(15)可知,信号的脉冲宽度越窄,即带宽越宽,则峰值信噪比越大。该结论与文献[27]中的实验结果一致。

3 仿真分析

根据第2节分析可知,初始信号影响时间反演性能的主要参数为频率和脉冲宽度。针对这2个参数,本文采用数值方法开展仿真分析,并进行验证。

3.1 频率

对于初始信号的频率,本文选择载波频率分别为2.4,2.8,3.2 GHz的高斯脉冲。初始信号如图3所示,1/e脉冲宽度均为3 ns。时间反演腔如图4所示,为准2维矩形腔体,尺寸为900 mm×700 mm×43.18 mm。其中,端口为BJ26波导,腔体中间有一个半径为20 mm的圆柱体,壁面和圆柱体材料均为理想导体。利用CST软件进行时间反演仿真,得到不同频率下的峰值信噪比,如表1所列。由表1可知,峰值信噪比随频率的增加而减小。仿真分析结果与第2节理论分析结果一致。

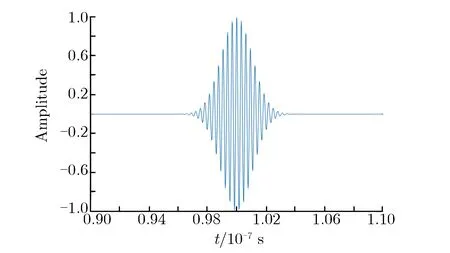
图3 初始输入信号Fig.3 Initial input signal

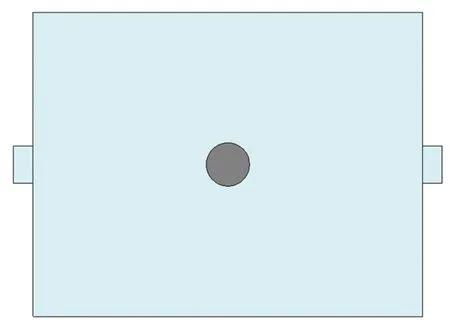
图4 时间反演腔Fig.4 Time reversal cavity

表1 不同频率下的峰值信噪比Tab.1 Peak signal-to-noise ratios at different frequencies

3.2 脉冲宽度

分析脉冲宽度对峰值信噪比的影响,本文选择初始信号的载波频率为2.4 GHz,1/e脉冲宽度分别为3,5,10 ns的情况。TRC结构与第3.1节相同,不同脉冲宽度下的峰值信噪比如表2所列。由表2可知,峰值信噪比随脉冲宽度的增大而减小,与本文的理论分析结果一致。

表2 不同脉冲宽度下的峰值信噪比Tab.2 Peak signal-to-noise ratios under different pulse widths

在脉冲宽度分析中需注意的是,当脉冲宽度大于腔体传播时间常数时,主瓣将会与旁瓣产生叠加[21]。这不仅会影响主瓣波形,而且会导致噪声信号的最大值不在t=0时刻附近。脉冲宽度为20 ns调制方波信号的时间反演结果如图5所示。该例中,初始信号是载波频率为2.4 GHz,脉冲宽度为20 ns的方波调制信号,且时间反演腔与图4相同,传播时间常数约为3 ns。这种情况下,真实信噪比可能会与理论分析结果有差异。

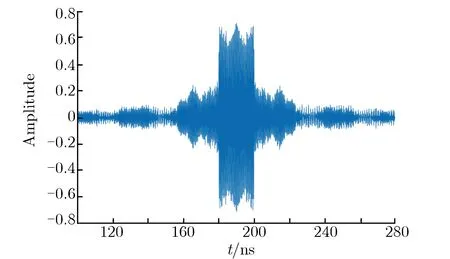
图5 脉冲宽度为20 ns调制方波信号的时间反演结果Fig.5 Time reversal result of modulated square wave signal with pulse width of 20 ns

4 结论

本文研究了高Q值时间反演腔系统中初始信号对反演性能的影响,并给出了频率和脉冲宽度影响的基本规律。初始信号的频率越大,则反演信噪比越小;脉冲宽度越宽,即带宽越窄,则反演信噪比越小。对于频率的影响,需注意TRC的不变条件。如需建立高频时间反演系统,提高系统的反演性能时,可能需减小腔体表面积并(或)提高腔体壁面的电导率等参数。在脉冲宽度的影响分析中,脉冲宽度变化将会导致带宽变化,这将会引起积分符号中传递函数的范围变化。这些因素相互关联,不可独立分割,难以完整的集中在一起分析。但从整体上看,本文的近似分析方法是合理的,得到的基本规律与数值仿真结果一致,可为提高TRC系统的反演性能提供借鉴。