短脉冲信号阵列接收的Keystone变换预处理方法

巴 涛,汪海波,张海川,庄 俊,戎 磊,席麒钧

(先进高功率微波技术重点实验室;西北核技术研究所: 西安 710024)

一些电真空微波产生器件,可产生高峰值功率短脉冲的微波辐射。产生此类微波辐射的微波源有重要的实用价值[1-3]。

数字阵列接收处理能利用空域滤波处理的优势,可实现自适应波束形成、干扰对消等[4-6]。阵列接收系统在处理短脉冲信号时,会遇到有效孔径丢失的问题,产生的原因是:短脉冲信号的能量在时域上集中,以一定角度斜入射到接收阵列时,会产生明显的依次“到达”现象。表现为靠近辐射源的阵列单元先接收到信号,远离辐射源的阵列单元后接收信号;由于信号脉冲短,当远离辐射源的阵列单元接收到信号时,靠近辐射源的阵列接收信号已经结束。上述现象导致阵列的有效长度降低,使达波方向测量、估计的分辨能力下降,阵列合成的信噪比下降。

短脉冲信号本质上是一种宽带信号,接收阵列处理宽带信号的主要方法有窄带划分法[7]和聚焦法[8]。窄带划分法是将信号分解为多个子带,在子带内进行处理,然后对所有子带结果进行非相参累加,会使信号的分辨率损失;聚焦法是利用不同频率点上的导向矢量的差异构造聚焦变换矩阵,将不同频点的数据变换到中心频点,是一种有效方法,然而需针对每个方向设计不同校准网络,计算复杂度高。

Keystone变换广泛应用于合成孔径雷达、脉冲多普勒雷达等重频体制,实现慢时间包络对齐[9-13],也应用在声呐的宽带自适应波形形成中[14]。Keystone变换的优点在于校准处理时,不针对某个特定方向,可实现各方向的盲校准,无须针对每个子带构造延时不同的滤波器组。Keystone变换可作为阵列接收的预处理方法,能有效校准包络的时延,不影响其他空域处理能力。

1 阵列接收信号模型

阵列接收处理在雷达、声呐、无线电通信及射电天文学等诸多领域具有广泛应用。阵列接收处理指采样空间分布的多个传感器采集包含期望信号和噪声的物理场波形后,通过对多传感器信号进行特定的空域滤波处理,或进行波达方向估计等,提升整个系统的信号质量及抑制其他方向的干扰。阵列接收处理的特点是,每个接收单元都具备正交下变频和采样的能力,图1为阵列接收处理短脉冲信号示意图。图1中,可把每个接收单元看成一个独立的接收机。

图1 阵列接收处理短脉冲信号示意图Fig.1 Schematic diagram of array receiving and processing short pulse signals

假设有N个接收阵列单元依次排开,阵元间距为d。中心频率为fc的短脉冲信号x0(t)可表示为

x0(t)=a(t)ej2πfct

(1)

其中:a(t)是短脉冲的包络;t为时间;fc为短脉冲信号中心频率。假设该信号以与垂直方向呈θ角斜入射到接收阵列上,那么第n(0≤n≤N-1)个阵元接收到的信号,变换到基带可表示为

y(nd,t)=x0(t-τnd)e-j2πfct

=a(t-τnd)e-j2πfcτnd

(2)

其中,τnd为每个阵元接收到信号的物理延时,可表示为

(3)

其中,c为场传播速度。由式(2)和(3)可知,不同的入射角度不仅影响各个阵元的相位,也影响信号的包络。若短脉冲的包络a(t)的有效宽度为τW,则实际起作用的阵元数量可表示为

(4)

由式(4)可知,当sinθ较大,且τW较短时,会导致Leff小于阵列的物理孔径。

2 基于 Keystone 变换预处理的短脉冲预处理方法

2.1 虚拟孔径原理

为了便于表述,假想一个长度为(N-1)d的连续接收孔径,类似于式(2),沿长度方向,坐标为l处的接收信号基带表示为

(5)

将式(5)变换到频域可表示为

y(l,f)=FT(x(l,t))=A(f)e-j2π(f+fc)τl

(6)

其中:FT(·)为傅里叶变换;f∈[-B/2,B/2],B为信号的有效带宽。利用Keystone变换对接收阵列的坐标做变换,表示为

(7)

其中:l为变换前的坐标;l′为Keystone变换后的坐标;α为尺度因子,大小与频率相关。采样间隔对应关系可表示为

(8)

式(6)经过坐标变换后可表示为

(9)

经式(9)变换后的l′能实现信号的包络对齐,来波的角度信息只体现在信号的相位项中,且与入射波角度关系保持与式(3)相同。

坐标变换后对应的孔径位置,并不是真实存在的孔径位置,需通过真实孔径的采样数据对虚拟孔径位置的采样结果进行插值处理。

2.2 算法的实现

从N个接收阵列获得基带采样序列,表示为x(nl,mt)。其中,nl是阵列的采样序号,nl= 1, 2, …,N;mt是时间采样序号,mt=1, 2, …,M,采样间隔为Δt,M为处理缓存的总长度。对该基带采样序列进行离散傅里叶变换,得到数字频域,表示为

y(nl,mf)=FFT[x(nl,mt)]

(10)

其中,FFT(·)为离散傅里叶变换;mf是数字频域采样序号。

Keystone变换的辛格(sinc)函数插值实现方式可表示为

(11)

其中,nl′是虚拟阵列的采样序号。sinc函数表示为

(12)

尺度因子α可表示为

(13)

式(11)也可通过线性调频Z变换 (Chirp-Z-transform, CZT)的方法实现Keystone变换,具体过程为

yKeystone(nl′,mf)=

(14)

其中,k为线性调频Z变换之后的空域采样序号。

对式(11)和式(14)中的yKeystone(nl′,mf)进行逆傅里叶变换,可获得包络延时校准完的基带信号,表示为

x(nl′,mt)=IFFT(yKeystone(nl′,mf))

(15)

式(15)中来波方向只体现通道之间的相位关系。

根据上述算法表述,确定了短脉冲阵列接收的Keystone变换预处理流程,如图2所示。经图2中的流程处理后,阵列处理短脉冲信号可完全类似于处理窄带信号,可进行类似于波达方向(direction of arrival,DOA)估计、空域滤波处理等。

综上,本文所提出的方法是短脉冲的阵列接收的预处理方法,其后端空域处理措施与窄带系统完全类似。

根据图2对Keystone变换预处理流程的计算复杂度进行分析。对于各种硬件信号处理器而言,乘法计算资源消耗量远大于加法。本文中FFT算法和CZT算法的计算复杂度分析结果参考了文献[15]。算法过程中包含了前后两次FFT乘法计算及CZT变换的乘法计算,复杂度量级分别为MNlog2N,3MNlog2N,算法过程中乘法计算复杂度量级总计为4MNlog2N。如果采用sinc函数插值方法,乘法计算复杂度量级为MNlog2N+MN2。与sinc函数插值方法相比,采用CZT变换的方法计算复杂度更低。

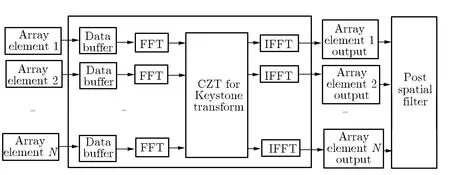
图2 短脉冲阵列接收的Keystone变换预处理流程Fig.2 Keystone transform pre-processing process for array-received short pulse

3 数值计算结果及分析

3.1 单个方向信号情况

设定短脉冲信号的中心频率为6 GHz,脉冲宽度为5 ns,单个脉冲信噪比为15 dB。接收阵列单元间距为半波长,阵元数为60,整个阵列长度为1.5 m。设置入射波与阵列法线的夹角为60 °。

通过上述仿真设置构造各接收阵列的时域信号分布,如图3所示。图3中,红色部分为短脉冲到达阵列的时间和天线序号分布。由图3可见,入射波倾斜入射到阵面上,包络在时域上不能完全对齐,表现为红色部分为斜线;在同一个时刻,有效接收阵元数降低了约一半。

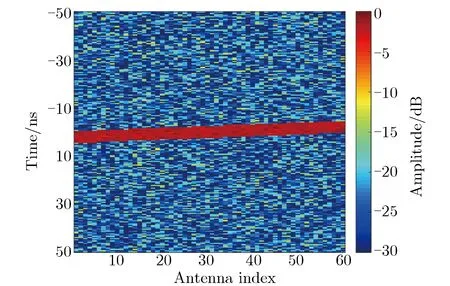
图3 各接收阵列的时域信号分布 Fig.3 Time-domain signal distribution of each receiving array

图4和图5分别为利用sinc函数插值方法和CZT变换方法实现的Keystone变换预处理结果。由图4和图5可见,经过Keystone变换处理之后,短脉冲信号的包络延时实现了校准,表现为红色部分从斜线拉成了直线。

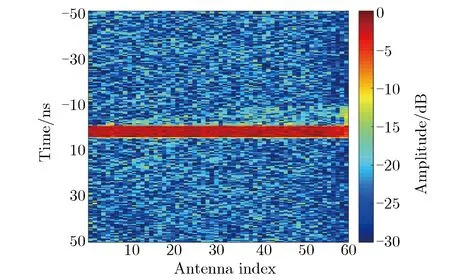
图4 通过sinc函数插值实现的Keystone变换预处理结果Fig.4 Pre-processing results of Keystone transform implemented by sinc function interpolation

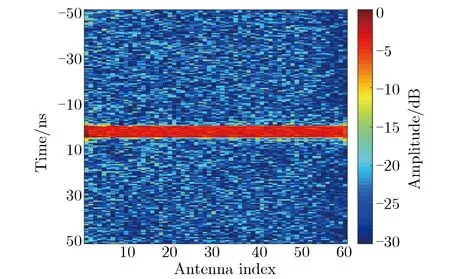
图5 通过CZT变换方法实现的Keystone变换预处理结果Fig.5 Pre-processing results of Keystone Transform by CZT transform

Keystone变换仅对短脉冲信号的包络延时进行盲校准,不影响后续进行空域信号处理。本文以空域FFT实现的空间谱估计为例,展示Keystone变换实现包络校准对空间谱估计的性能的改善。

利用空域FFT对图3信号进行的DOA估计,结果如图6所示。利用空域FFT对图5信号进行的DOA估计,结果如图7所示。由图6与图7可见,图7的DOA估计结果比图6尖锐。另外,由图6可见,在脉冲前沿和后沿会出现DOA形状畸变的现象。产生该现象的原因是未经过包络校准的阵列信号不能同时到达阵面。而Keystone变换能够将短脉冲信号校准到相同的时间单元,达到更好的阵元利用效率,且不同时间单元之间不产生相互干扰。

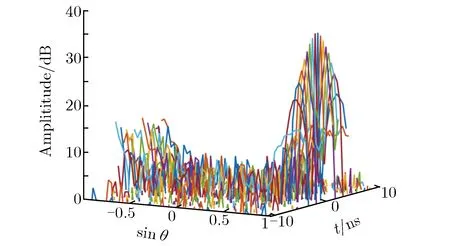
图6 利用空域FFT对图3信号进行的DOA估计结果Fig.6 DOA estimation results of Fig. 3 signals by spatial FFT

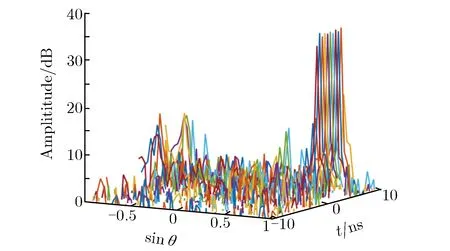
图7 利用空域FFT对图5信号进行的DOA估计结果Fig.7 DOA estimation results of Fig. 5 signals by spatial FFT

3.2 两个方向信源情况

本文所述的Keystone预处理方法无须针对不同的入射方向进行补偿,能自动适应不同的入射短脉冲波形。

设置2个幅度、脉宽、信噪比和中心频率相同,且与之前的仿真设计一致,到达角分别为30°和60°的入射信号。图8为阵列各阵元接收2个入射信号的时域波形。图9为经CZT变换实现的Keystone变换的时域波形。

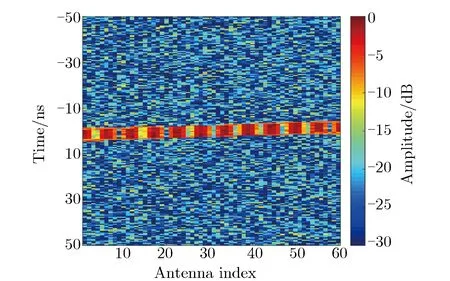
图8 各接收阵列的时域信号分布Fig.8 Time-domain signal distribution of each receiving array

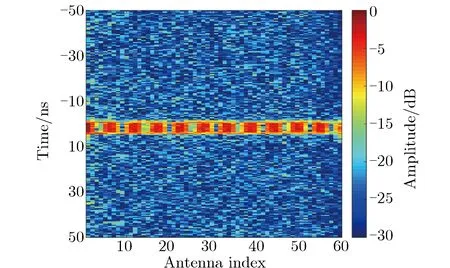
图9 通过CZT变换方法实现的Keystone变换预处理结果Fig.9 Pre-processing results of Keystone transform by CZT transform

由图8可见:2个入射波在接收阵列上产生了干涉现象;信号包络等相位面方向与阵面法线方向不垂直。由图9可见,信号包络等相位面获得了校准。

利用空域FFT对图8和图9信号进行DOA估计的结果如图10所示。由图10可见,图10(b)的DOA估计效果明显比图10(a)尖锐;图10(a)中分辨出2个方向的入射信号较难,而图10(b)中更容易区分出2个方向的入射信号。

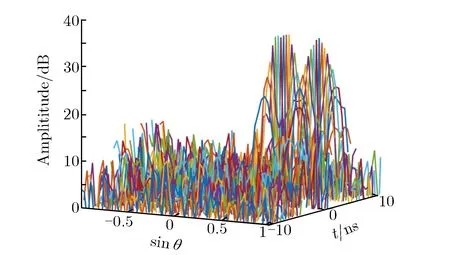
(a) Fig.8 signals

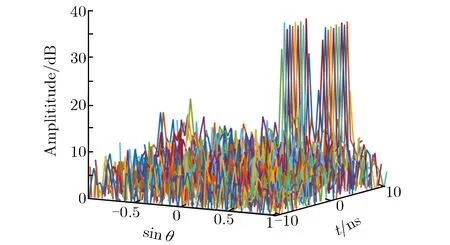
(b) Fig.9 signals

4 结论

本文将Keystone变换引入短脉冲阵列接收处理问题中,无须针对每个子带专门进行设计补偿滤波器,就能实现在均匀线阵中,短脉冲包络到达延时校准的效果。该方法可作为其他信号处理措施的预先处理方法,能充分利用整个接收阵列的物理孔径。但该方法的最大局限在于Keystone变换的虚拟孔径原理要求阵列间距相同,因此该方法只适应于均匀线阵。