方波脉冲下高低剩磁非晶和纳米晶磁芯磁化特性

魏艺卓,陈 立†,孙凤举,王志国,,刘彦博,张维森,张 峰,师伟皓

(1. 西安交通大学 电气工程学院,西安 710049;2. 西北核技术研究所,西安 710024)

直线型变压器驱动源(linear transformer driver,LTD)作为一种直接驱动脉冲功率源,具有结构紧凑、模块化和可重复频率工作的优点[1-3]。磁芯在LTD中起初次级能量耦合作用,脉冲磁导率、磁感应增量及损耗等参数显著影响输出波形及能量传输效率[4-5]。磁芯磁化过程与磁芯材料、处理工艺及激励特性等诸多因素有关[6-8],在实际工况或近似工况下获取磁芯的磁化特性参数,可为LTD磁芯设计和预估LTD输出特性提供关键支撑。

目前,国内外研发的LTD一般采用硅钢叠片或非晶合金磁芯,采用双绕组测量方法对2种磁芯进行测试,研究了磁芯伏秒数对输出波形的影响及磁芯损耗、磁导率等特性参数随磁化速率的变化关系,结果表明,与硅钢叠片相比,非晶合金更适用于快前沿脉冲[9-14]。近些年,方波LTD的应用逐渐增加,具有纳秒量级上升沿和一定时间平顶的方波能更好地应用于闪光照相、强激光和高功率微波等驱动源[15],百纳秒到微秒量级方波脉冲可用于研究不同参数脉冲诱导癌细胞凋亡的效应及机理[16-17]。但现有磁化特性研究基于近似双指数脉冲激励,频谱范围较窄,可能无法适用于宽频谱方波脉冲,且目前关于磁场热处理方式对磁芯性能影响的研究主要集中在材料科学与工程领域[6,18],方波脉冲激励下不同剩磁磁芯的磁化特性会发生改变[19]的响应规律尚未明晰,需基于应用环境进一步测试。

为更好地满足百纳秒到微秒量级方波LTD磁芯的设计,并为类似工况下的工作特性研究提供基础数据,本文建立了频率可调的磁芯参数测试平台,获取了高、低剩磁非晶和纳米晶磁芯在百纳秒到微秒量级方波脉冲激励下脉冲磁导率、磁感应增量及损耗等参数随等值频率的变化关系。通过曲线拟合建立了损耗随频率的变化关系,计算了不同工作频率下非晶态磁芯的损耗。

1 方波脉冲磁化特性测试系统

1.1 非晶态磁芯参数

选用四川力源电子有限公司研制的高、低剩磁铁基纳米晶和非晶磁芯作为研究对象,以A,B分别代表1K107纳米晶和1K101非晶材料,1,2分别代表经纵向磁场热处理得到的高剩磁和横向磁场热处理得到的低剩磁。将4种磁芯编号为A1,A2,B1,B2,磁环外形尺寸如图1所示,薄带间使用SiO2材料作为绝缘涂层,磁芯静态参数如表1所列。表1中:δ为带材厚度;ρ为电阻率;η为占空比;Le,Ae,Ve分别为磁路有效长度、磁芯有效截面积及有效体积。

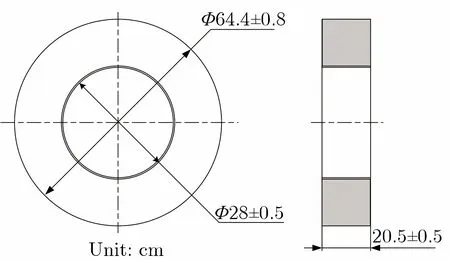
图1 磁环外形尺寸Fig.1 External dimensions of magnetic cores

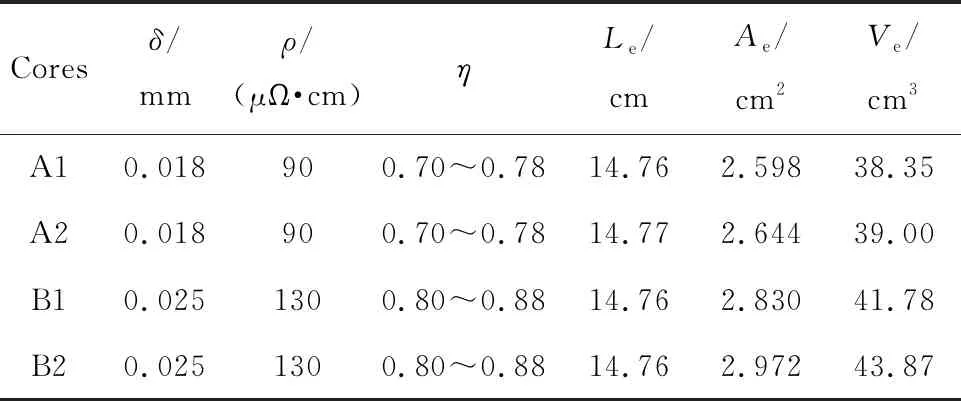
表1 磁芯静态参数Tab.1 Static parameters of magnetic cores

1.2 可调频方波脉冲测试电路

为获得百纳秒到微秒量级方波脉冲下的磁化特性,搭建了双绕组电路,可调频方波脉冲磁芯特性测试平台如图2所示。C为储能电容,由高压直流源经隔离电阻充电至U0,开关闭合后,电压通过约8 μH的激磁电感L施加至磁芯,磁芯不饱和时相当于开路,可获得方波脉冲激励。剩磁纳米晶和非晶磁芯测试参数如表2和表3所列。初、次级绕组匝数N1,N2均为3,采用同轴分流器测量初级励磁电流I(t),采用高压探头测量次级开路电压U(t)。实验前进行直流反向去磁。该平台可产生脉冲前沿为10～30 ns,脉冲宽度为0.2～10 μs的方波脉冲。

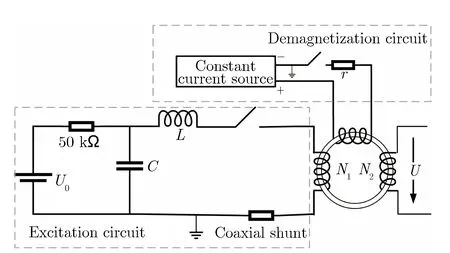
图2 可调频方波脉冲磁芯特性测试平台Fig.2 Frequency tunnable platform with squre pulse magnetic core characteristic

表2 剩磁纳米晶磁芯A1/A2测试参数Tab.2 Test parameters of nanocrystalline magnetic core A1/A2 with different remanences

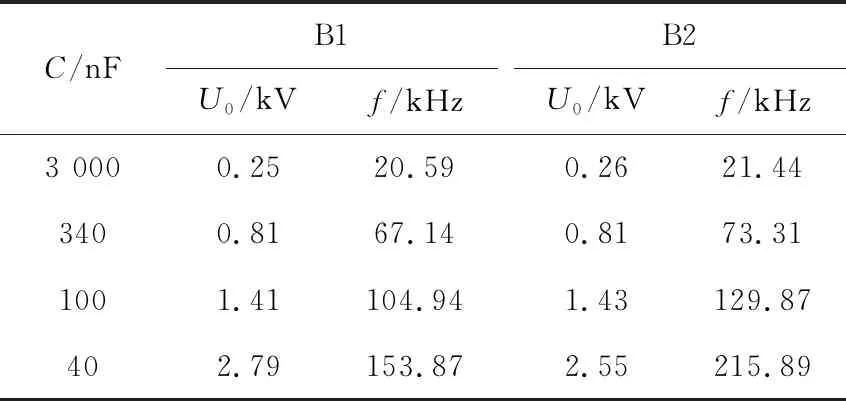
表3 剩磁非晶磁芯B1/B2测试参数Tab.3 Test parameters of amorphous magnetic core B1/B2 with different remanences

1.3 测试结果与处理方法

170 kHz下高剩磁纳米晶磁芯A1的电压和电流波形如图3所示。利用Savitzky-Golay滤波算法进行平滑降噪,滤除噪声的同时确保信号形状和宽度不变[20]。由于测试过程中存在温度变化及电源电压不稳定等因素影响,测试信号会产生零点漂移,需在测试结果的基础上减去零点漂移平均值,提高测量波形的准确度和分辨率。

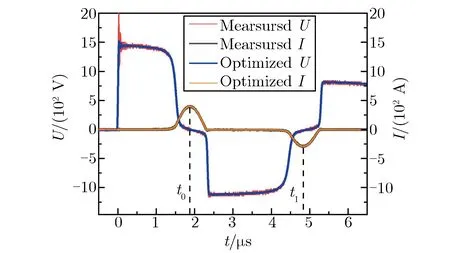
图3 170 kHz下高剩磁纳米晶磁芯A1的电压和电流波形Fig.3 Voltage and current waveforms of high remanence nanocrystalline magnetic core A1 at 170 kHz

t0和t1分别为电流到达第一个和第二个峰值的时间,等值频率f可表示为

(1)

在LTD中,f可近似表示为

(2)

其中,td为LTD空载实验得到的第一个脉冲的持续时间。

磁场强度H和磁感应强度B可表示为

(3)

(4)

2 磁化特性测试结果及分析

测量磁芯的磁滞回线可得到磁感应强度增量、脉冲磁导率和磁滞损耗等参量,不同等值频率下,4种磁芯的磁滞回线如图4所示。

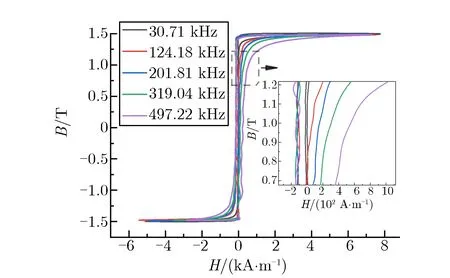
(a) A1

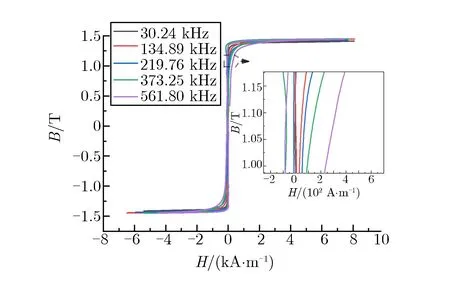
(b) A2

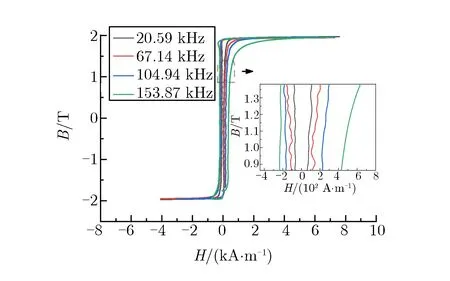
(c) B1

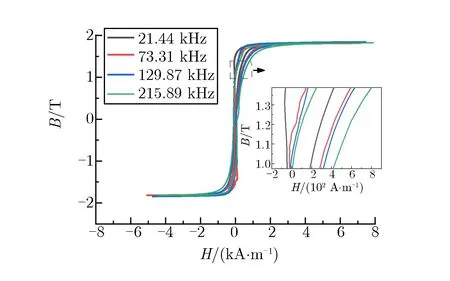
(d) B2

2.1 最大磁感应增量

本文采用直流去磁方式,磁芯的磁感应强度增量可表示为

ΔB=Br+Bs

(5)

其中,Br,Bs分别为径向和纵向磁感应强度。

由式(5)计算得到4种磁芯的最大磁感应强度增量,如表4所列。

表4 4种磁芯的最大磁感应强度增量Tab.4 Maximum magnetic induction increment of 4 magnetic cores

根据法拉第电磁感应定律,磁芯的伏秒积可表示为

(6)

其中,S为磁芯的横截面积。

在LTD中磁芯饱和会引起输出电压降低、脉冲宽度减小等[5]。在方波脉冲下,利用电压峰值与脉冲宽度计算所需伏秒积,合理选择磁芯的材料、处理工艺及截面积等参数。

由图4及表4可知:在脉冲条件下,4种磁芯均具有较高的矩形比;磁芯的饱和磁感应强度和剩余磁感应强度与等值频率无关;磁感应强度增量仅与磁芯材料和处理工艺有关;非晶材料高于纳米晶材料,经纵向磁场处理的材料高于经横向磁场处理的材料。

2.2 最大相对磁导率

磁导率反映了磁性材料约束磁力线的能力,最大相对磁导率可表示为

(7)

利用已测得的磁滞回线数据可得到4种磁芯最大相对磁导率随等值频率的变化关系,如图5所示。

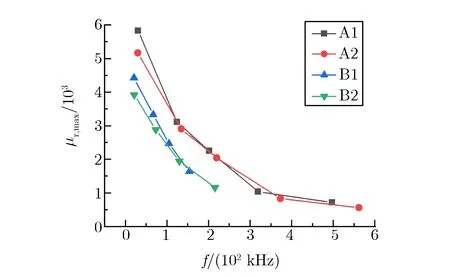
图5 4种磁芯最大相对磁导率随等值频率的变化关系Fig.5 μr,max vs. f of 4 magnetic cores

由图5可见,随着等值频率的增加,4种磁芯的最大相对磁导率迅速降低。在相同等值频率下,非晶磁芯的相对磁导率低于纳米晶磁芯,不同热处理工艺得到的高、低剩磁磁芯的磁导率相差较小,可见该参数主要取决于材料种类及工作频率。

2.3 平均脉冲磁导率

由于磁芯磁导率变化范围较大,常采用平均脉冲磁导率估算激磁电感,表示为

(8)

利用已测得的磁滞回线数据可得到4种磁芯平均脉冲磁导率随等值频率的变化关系,如图6所示。

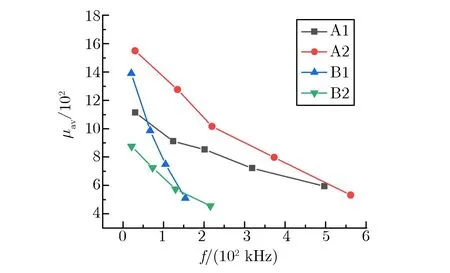
图6 4种磁芯平均脉冲磁导率随等值频率的变化关系Fig.6 μav vs. f of 4 magnetic cores

由图6可见,随着等值频率的增加,4种磁芯的平均脉冲磁导率与最大相对磁导率具有相同的变化趋势。但在相同等值频率下,低剩磁纳米晶磁芯的平均脉冲磁导率高于高剩磁纳米晶磁芯;当等值频率小于60 kHz时,高剩磁非晶磁芯的平均脉冲磁导率高于高剩磁纳米晶磁芯,可见该参数受磁感应强度增量和工作频率共同影响。

2.4 磁芯损耗

磁芯在磁化过程中的混乱时间及磁畴空间分布难以采用微观物理模型进行准确描述,现有的研究多基于工程应用环境下得到的实验数据建立宏观模型计算磁芯损耗[21]。

磁芯密度为单位体积磁芯损耗的能量,正比于磁滞回线包围的面积,可表示为

(9)

其中,N为一个采样周期内可充分表示磁滞回线的数据点个数。

大量研究表明,每周期磁滞损耗与频率无关,涡流损耗、剩余损耗为频率的幂函数。双对数坐标可将幂函数关系变化为线性关系,更直观体现磁芯损耗的主导机制随频率的变化关系,在该坐标系中建立每周期4种磁芯的损耗W/f随等值频率f的变化关系,如图7所示。

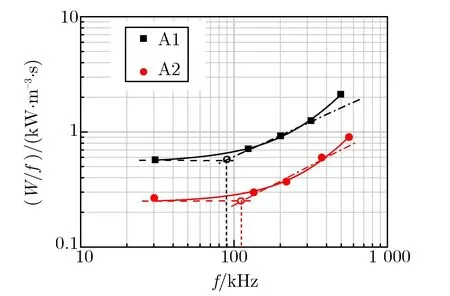
(a) Nanocrystalline cores

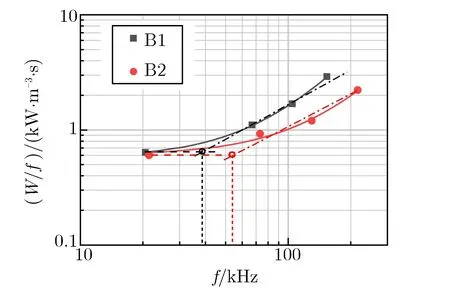
(b) Amorphous cores

根据周期损耗变化趋势将数据划分为不同主导机制的数据集,并分别进行线性拟合,如图7中虚线所示。由图7可见,纳米晶磁芯在100 kHz左右,非晶磁芯在40 kHz左右出现涡流损耗主导现象,低剩磁磁芯滞后于高剩磁磁芯。

4种磁芯的损耗随等值频率的变化关系如图8所示。

图8 4种磁芯的损耗随等值频率的变化关系Fig.8 W/f vs. f of 4 magnetic cores

由图8可见:工作条件相同时,非晶磁芯的损耗高于纳米晶磁芯;磁芯材料相同时,低剩磁磁芯的损耗更低;随着等值频率的增加,非晶磁芯损耗以更快速率随等值频率增加而增大。

文献[17]指出利用等值频率表征损耗比利用磁化速率等其他参数表征更直观,但给出的直线拟合公式缺少物理机制解释。

动态磁化过程中,磁芯损耗包括磁滞损耗Whys、涡流损耗Wcls及剩余损耗Wexc,经典计算可表示为[22]

Wloss=Whys+Wcls+Wexc

(10)

其中:r为涡流半径;ρ为电阻率;k1,k2为常数;Bm为最大磁感应强度。

上述实验条件下,磁芯均达到饱和磁感应强度,故基于式(10)拟合得到磁芯损耗的计算公式,表示为

WA1=0.004 5f2+0.93f+534.52

(11)

WA2=0.001 7f2+0.24f+241.99

(12)

WB1=0.082f2+2.57f+551.29

(13)

WB2=0.027f2+1.59f+586.03

(14)

为验证公式的准确性,任意选取若干等值频率进行实验验证。表5和表6为实测损耗和计算损耗的对比,以相对偏差作为评价指标判断模型的准确性,表示为

(15)

其中:WMEAS为实测磁滞回线积分得到的损耗;WCALC为上述式(11)-式(14)计算得到的损耗。

由表5和表6可知,磁芯实测损耗与计算损耗的相对偏差小于5%,证实了本文损耗模型的准确性。

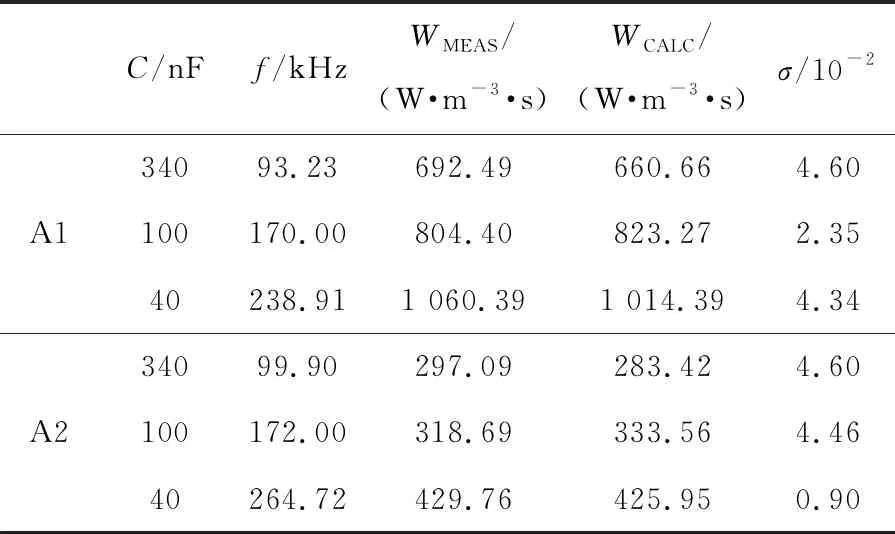
表5 纳米晶磁芯实测损耗与计算损耗对比Tab.5 Measured and calculated losses of nanocrystalline cores

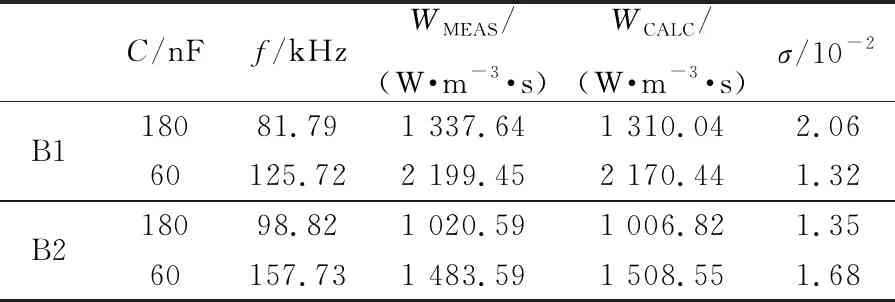
表6 非晶磁芯实测损耗与计算损耗的相对偏差Tab.6 Relative deviation of measured and calculated losses of amorphous cores

3 结论

本文建立了百纳秒到微秒量级可调频方波脉冲磁化特性测试系统,针对高剩磁和低剩磁非晶磁芯和纳米晶磁芯进行测试,获得了磁芯损耗随等值频率变化的关系式,可用于LTD磁芯损耗估算及磁芯等效电路模型的建立,获得的结论为:

(1) 在工频测试条件下,同种材料低剩磁磁芯的磁感应强度增量远小于高剩磁磁芯,但在高频方波条件下具有与高剩磁磁芯相近的磁感应强度增量。这可能是高频下涡流损耗较大造成的,由损耗分离原理可知,涡流损耗引起磁滞回线的横向展宽,因此剩磁点会发生改变。

(2) 非晶磁芯在0～200 kHz,纳米晶磁芯在0～600 kHz的测试频带内,相同等值频率下的高、低剩磁磁芯最大相对磁导率相差较小,非晶磁芯的最大相对磁导率低于纳米晶磁芯。但平均脉冲磁导率受磁感应强度增量和工作频率共同影响,低剩磁纳米晶磁芯的平均脉冲磁导率高于高剩磁纳米晶磁芯,高剩磁非晶磁芯在频率小于60 kHz时的平均脉冲磁导率高于高剩磁纳米晶磁芯。

(3) 非晶磁芯在约40 kHz,纳米晶磁芯在约100 kHz的测试频率出现涡流损耗主导现象,低剩磁磁芯滞后于高剩磁磁芯。非晶磁芯在0～200 kHz,纳米晶磁芯在0～600 kHz的测试频带内,同种材料的低剩磁磁芯损耗更低,非晶磁芯受带材厚度限制,具有更高的磁芯损耗且以更快的速率随等值频率增加而增大。

(4) 低剩磁磁芯在高频下同样具有较高的磁感应强度增量,且自恢复能力较强,可用于高压多脉冲感应加速腔。在磁脉冲压缩系统中,多采用磁滞回线矩形度较高的高剩磁磁芯。与纳米晶磁芯相比,非晶磁芯同时具有磁感应强度增量大的优势和能量传递效率较低、磁导率较低的缺陷,在进行LTD等脉冲变压器选型时需进行综合比较。