基于多球中子谱仪的解谱算法研究现状

范启蒙,吕 宁,过惠平,张全虎

(火箭军工程大学,西安 710025)

在航空航天[1-3]、核能工程[4]及加速器物理[5-6]等诸多领域,都需知中子数随能量的分布,即中子能谱。根据实际应用场景的不同,中子能量可覆盖从热中子到GeV量级的极宽能量范围,一般探测器难以满足要求。20世纪60年代,Bramblett等[7]设计出了多球中子谱仪,由一系列大小不同的慢化球体包裹着热中子探测器组成,慢化球的体积大小与材料性质影响其慢化能力,对应不同的能量敏感区域,因此,多球中子谱仪适用于宽能量段能谱测量。基于探测器的响应计数求解中子能谱就是中子解谱问题,一般情况下,响应计数的数目等于探测器的数目,远小于宽能量段范围内待求解未知量的数量,所以中子解谱问题又叫作“少道解谱”。

如一个问题的解满足存在性、唯一性和稳定性,则称为适定问题,否则称为非适定问题[8]。少道解谱是一个典型的非适定问题。考虑到中子能谱的客观实在性,少道解谱问题的解是必然存在的;考虑到能谱分布的多样性,不同的中子能谱可能会引起探测器相同的响应,在解谱过程中需尽可能多地掌握实际中子能谱的信息,以得到与实际相符的能谱;考虑到核反应过程的随机性及测量环境,探测器数据必会被噪声污染,在解谱过程中需采用合适方法消除噪声影响,保证求解能谱的稳定性。前期已有相关文献对中子解谱算法进行了综述[9-10],但只是介绍了不同算法的具体原理,未能在统一框架下研究不同解谱算法的实质。实际上,求解非适定问题最大的困难来自于先验信息的缺失,因此,要准确求解中子能谱,必须加入能谱先验信息。本文主要从利用先验信息的方面介绍不同的解谱方法。

1 多球中子谱仪的工作原理

多球中子谱仪是由多个热中子探测器组成的探测系统,每个探测器的灵敏区域位于慢化球的中心,慢化体的材料纯度要高且密度均匀,以保证对中子能量响应的各向同性。早期多球中子谱仪采用6LiI(Eu)闪烁体探测器,慢化体材料是聚乙烯,慢化后的中子在探测器中发生6Li(n,α)3H反应,产生的α粒子与3H在晶体内损失能量产生闪光,经光电倍增管放大后转化为电信号,送入后续电子学电路进行处理。图1为早期多球中子谱仪示意图[7]。

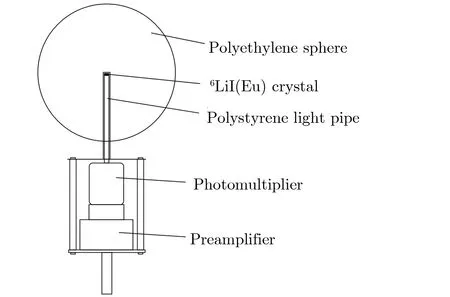
图1 早期多球中子谱仪结构示意图Fig.1 Schematic diagram of early multisphere neutron spectrometer

对于仅由聚乙烯组成的慢化球,体积较小的球慢化能力较弱,更易捕获热中子,同时低能中子经过一定程度的慢化后变为热中子,也易被探测,但由于对快中子的慢化程度不够,大部分快中子都将逃逸,因此体积较小的慢化球仅对低能区中子的探测效率较高。体积较大的球慢化能力强,大部分低能中子被慢化材料吸收,高能中子经过较大程度的慢化,抵达球中心时变成了易被捕获的热中子,因此体积较大的球对高能区中子探测效率更高。为扩展探测能量上限,可在聚乙烯慢化球中加入慢化能力更强的金属材料。德国联邦物理技术研究院(Physikalisch-Technische Bundesanstalt,PTB)研发了一套基于3He正比计数器的多球谱仪系统,在聚乙烯球的基础上,增加了铅、铜等材料制成的球壳,可与聚乙烯球组合改善谱仪在高能端的响应[11-12]。在实际探测中,可灵活选用慢化球尺寸组合和慢化球材料。图2为PTB设计的多球中子谱仪结构示意图。

图2 PTB设计的多球中子谱仪结构示意图Fig.2 Schematic diagram of multisphere neutron spectrometer designed by PTB

通常用响应函数R(E)描述不同尺寸谱仪的性质,R(E)是入射中子能量E的函数,表示该谱仪对不同能量中子的响应计数,每个谱仪对应一条能量响应曲线,因此,多球中子谱仪的性质用一簇响应函数曲线来表示。图3为PTB设计的多球中子谱仪部分尺寸慢化球的响应函数。

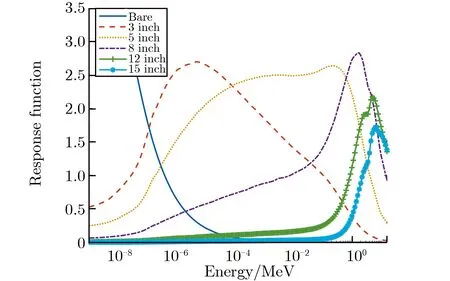
图3 PTB设计的多球中子谱仪部分尺寸慢化球的响应函数Fig.3 Response function of multisphere neutron spectrometer designed by PTB

设中子能谱为Φ(E),第k个探测器的响应函数为Rk(E),那么响应计数Nk可表示为

(1)

式(1)为第一类Fredholm方程的形式。为便于数值计算,将式(1)写成离散形式,设共有m个球探测器,能量范围被分为n段,每段长度为ΔEi(i=1,2,3,…n),通常m≪n。对应地将能谱Φ(E)和响应函数Rk(E)写成离散形式,考虑到实际测量中要不可避免地引入测量偏差,式(1)离散化得到

Nk+εk=∑Rkiφi,k=1,2,3,…m

(2)

其中,εk为测量偏差。式(2)即为测量方程,写成矩阵形式,表示为

N+ε=R·Φ

(3)

其中:N∈m×1为响应计数向量;ε∈m×1为测量偏差向量;R∈m×n为探测器响应矩阵,每一行表示一个探测器的响应函数;Φ∈n×1为中子能谱向量。

中子解谱就是基于式(3)的测量方程重建能谱Φ,解谱过程中主要面临2个困难:一是测量数据有限,实际获取的探测器读数的数量只与球的个数相同,基于有限个计数来重建连续分布的能谱Φ显然是不可能的;二是探测器的分辨率不高,反映到响应函数形状上,峰值可跨多个能量级,以致探测器最终获得的计数是宽能量范围内中子共同作用的结果,进一步增加了求解能谱的困难。

2 中子解谱方法

由式(3)可知,中子解谱在数学形式上是求解欠定线性方程组,由于方程个数远小于未知数个数,无法直接准确求解能谱。为准确求得能谱,必须考虑加入先验信息,对于先验信息的具体内容,既可是关于观测模型的,如每次观测值受噪声影响程度的大小,也可是关于能谱本身的,如能谱的平滑性、稀疏性等;对于先验信息的获取形式,既可通过随机性尝试来获得,也可通过基于已知样本的训练学习获得。本文重点从先验信息的利用角度介绍中子解谱方法。

2.1 最小二乘法

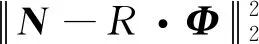
PLS=(N-R·Φ)T·(N-R·Φ)

(4)

为使性能指标达到最优,PLS关于Φ求导,并令导数等于0,通过矩阵运算可得到中子能谱的最小二乘解,表示为

Φ=(RT·R)-1·RT·N

(5)

最小二乘法一般更适合观测数据量多于待求未知量的超定问题,应用于欠定问题时,由于矩阵RT·R的奇异性,得到的解可能无法给出合理的物理解释。

加权最小二乘法是最小二乘法的改进,认为每次观测对应的噪声大小不同,即观测量的精度不同,在利用观测数据重建能谱时,对噪声较小的观测量赋予较大的权重,而对噪声较大的观测量赋予较小的权重,构造新的性能指标为

(6)

其中:CN为观测量的协方差矩阵,即偏差向量ε的协方差矩阵。PWLS关于Φ求导,并令导数等于0,通过矩阵运算得到加权最小二乘解,表示为

(7)

2.2 奇异值截断法

(8)

(9)

其中,Σ-1=diag(1/γ1,1/γ2,…,1/γn)。显然,对于值很小的对角线元素γi,其倒数1/γi将很大,意味着数据向量N中元素值的微小变化将会经放大后反映到能谱Φ中,造成解的不稳定。为此,强制将Σ-1对角线上大于1/γt的元素置0,即令Σ-1=diag(1/γ1,1/γ2,…,1/γt,0…,0),如此,解的稳定性得到极大改善。这种方法被称为奇异值截断法。如忽略测量偏差的影响,矩阵方程可表示为

N≈R·Φ

(10)

对式(10)中响应矩阵R直接进行奇异值分解,然后再采用相同的截断方法。两种方法相比,解的准确程度主要由奇异值的截断位置决定,而在加权最小二乘法中增加关于观测噪声先验信息的作用无法明显体现。

根据矩阵分析理论,Σ中较小的元素值对应信号的高频分量,这些分量更能反映信号的细节信息,但同时会造成解的不稳定,而Σ中较大的元素值对应信号的低频分量,或称主成分。从先验信息的角度,奇异值截断法认为能谱的慢变部分为主要成分,而忽略了快变部分,最终通过牺牲解的准确性来换取稳定性,因此采用奇异值截断法求得的能谱结果精度一般不高。

2.3 正则化方法

正则化方法是在第2.2节问题的基础上增加约束条件,约束条件的选择则体现了对先验信息的掌握程度,如将解的光滑性作为约束条件,则相当于已知解不是平滑变化的,因此更倾向于得到含有更多振荡成分的解。根据正则化项与待求未知量关系的不同,可将正则化方法分为线性正则化和非线性正则化方法两种。本文主要介绍线性正则化方法。

线性正则化方法中最常用的是Tikhonov正则化,可看成是最小二乘法的改进。少道解谱问题中观测数据量远小于未知数的数量,因此式(5)解中,矩阵RT·R是奇异的,无法得到具有物理意义的解。此外,由于R是由第一类Fredholm方程离散化得到的,逆算子是不连续的,这个特性会进一步恶化利用最小二乘法求得的结果,造成解的不稳定。为此,将解的平滑性(即Φ的导数)作为先验信息加入到目标函数中,得到的目标函数可表示为

L=(N-R·Φ)T·(N-R·Φ)+λΦT·H·Φ

(11)

其中:H为与求导阶数有关的系数矩阵[13],又叫做平滑矩阵;λ为正则化参数。求L关于Φ的偏导,并令导数为0,得到

Φ=(RT·R+λH)-1·RT·N

(12)

式(12)中,通过引入平滑矩阵H消除了RT·R的奇异性,从而得到稳定的解。通常H可选为单位阵,对应Φ的0阶导数。在线性正则化方法中,正则化参数λ的选取十分重要,直接决定了先验信息在求解中的权重,如λ很小,则对问题的非适定性改善有限,得到的结果仍有可能不稳定;如λ很大,那么平滑矩阵将起主要作用,在极端情况下得到

(13)

显然,式(13)结果精度很低,对应的是信号处理领域的匹配滤波解[14]。非线性正则化方法在目标函数中增加了关于Φ的非线性信息,具有代表性的是Fisher信息[15-16],本质上仍是增加了关于解的平滑性的先验信息,只不过是关于Φ的非线性关系。

无论是线性正则化还是非线性正则化,正则化参数的选择都是正则化方法中十分棘手的问题。由理论本质可知,因涉及解的稳定性与精度的矛盾,所以并不存在最优的正则化参数,如最后的结果在可接受的范围,则认为对应的正则化参数是合理的。总之,正则化是处理非适定问题的一种重要方法,本质是通过增加某一种类的先验信息来改善解的稳定性,但需合理选取正则化参数,调整先验信息在求解过程中的权重。

2.4智能算法

智能算法主要分为智能优化算法和神经网络方法两类。

智能优化算法主要是通过模仿自然界中生物之间的信息交互方式来求解优化问题,如基于基因遗传现象,鸟类、蚂蚁及蜜蜂等生物的觅食活动等,分别开发出遗传算法和粒子群算法等智能优化算法[17-18],已在中子解谱问题中得到了广泛应用[19-21]。智能优化算法都属于随机优化方法,利用随机优化方法求解中子解谱类的非适定问题,本质上是利用数据的随机性克服解的不稳定性,但对此类启发式自学习算法,不加约束的随机尝试将带来无法忍受的计算代价。因此,为利用大量可能的随机解来克服问题复杂性,必须合理设置算法的搜索空间。搜索空间的设置体现了对先验信息的掌握程度,一方面体现在建立的问题模型上,即优化问题中设置的目标函数,文献[22]将遗传算法和差分进化算法应用于中子解谱问题,指出不同目标函数会对解谱结果产生极大的影响;另一方面体现在优化算法的参数设置上,对于一个特定问题适用的算法参数,不一定适合另一个问题。综上所述,对于智能优化算法,需基于已掌握解的先验信息设置合理搜索空间,而后在迭代进化过程中通过随机尝试进一步挖掘解的先验信息,并通过智能算法自身的信息交互机制进一步强化。

与近年来兴起的人工智能方法相似,神经网络方法的准确性依赖于大量数据训练集,已应用于中子解谱[23-26]。用神经网络求解未知中子能谱之前,已通过特定训练机制掌握了数百对乃至更多对真实能谱Φ与探测器响应计数N之间的对应关系。衡量神经网络性能的重要指标是其泛化能力,即对于训练集中不存在的Φ与N,将N输入网络后成功重建Φ的概率。显然,与训练集中的Φ相似度更高的能谱,正确重建的成功率更高,这说明网络训练的过程就是一个学习先验信息的过程。对于泛化能力强的神经网络,通过设计合理的网络结构,能在已有先验知识基础上学习演化出更多的先验信息,适应更多更复杂的情形。

2.5 压缩感知算法

压缩感知(compressive sensing,CS)是近年来信号处理领域出现的一个极具潜力的研究方向,该理论指出待重建信号在满足稀疏性的前提下,可利用少量采样数据实现对信号的精确恢复[27-28],而中子解谱是利用少量的探测器响应计数重建极宽能段的能谱,因此中子解谱问题与压缩感知模型天然契合。以式(3)所示中子解谱模型为例,在CS框架下描述为(P0)问题,表示为

(14)

(15)

式(15)即中子解谱的压缩感知模型。为求解中子能谱,首先需构造合适的变换矩阵Ψ,即待求未知量的稀疏表示问题;其次要建立合适的重建算法求解(P0)问题。这两方面的问题也是压缩感知理论研究的核心问题。

关于稀疏表示问题,在CS理论出现之前就已有广泛深入的研究,实际上稀疏性是客观世界中广泛存在的一种事物属性,自然界的许多信号及大部分人工信号都可通过变换实现稀疏表示,如许多自然图像能通过离散余弦变换(discrete cosine transform, DCT)或小波变换(wavelet transform)实现压缩,而音频信号和通信信号通过傅里叶变换实现压缩,只是这类信号并不适合中子能谱的稀疏表示。为构建合适的变换矩阵,可采用字典学习的方法来构造[30-31],该方法本质上是通过基于大量样本的训练学习,构建出合适的稀疏表示矩阵。

关于重建算法,主要分为直接求解(P0)问题的贪婪算法[32]和用凸问题等价(P0)的凸松弛方法[30,33]两类。如已知待求未知量的稀疏度,可采用贪婪算法得到可行解。贪婪算法通过一系列局部优化来避免费时的全局搜索,但不能保证是全局最优解。凸松弛方法是利用连续或相对光滑的函数来替换高度不连续的l0范数,从而将非凸问题转化为凸问题,然后采用凸优化方法得到全局最优解。

从正则化的观点来看,压缩感知也是一种正则化策略,本质上是利用了解的稀疏性先验信息,考虑到稀疏性的广泛存在,且即使待求未知量不是自然稀疏的情况下,也可采用合适的方法构造变换矩阵进行稀疏表示,压缩感知理论在中子解谱领域具有很大的应用潜力。

3 结论

本文介绍了基于多球中子谱仪的中子解谱算法,从利用不同种类先验信息和先验信息的不同利用形式分析了各种解谱算法的特点。综上所述,中子解谱问题在数学形式上表现为求解欠定线性方程组,在物理本质上是先验信息的缺失,研究中子解谱算法须从充分挖掘利用先验信息的角度来考虑。此外,中子解谱问题与压缩感知理论模型天然契合,将压缩感知理论应用于中子解谱问题具有巨大潜力。采用压缩感知理论求解中子能谱时,关键是能谱的稀疏表示。由于信号处理领域中常用的稀疏变换矩阵不再适用于中子能谱,因此,字典学习方法更适合构造中子能谱的稀疏变换矩阵,在实际应用中可通过仿真模拟或实验测量先构建样本数据库,而后采用字典学习方法构建稀疏变换矩阵。在后续研究中,可考虑在先验信息的统一框架下,通过挖掘不同种类的先验信息来开发新的解谱算法。