基于静态随机存取存储器单粒子效应的中子能谱测量方法

秋妍妍,谭志新,易 晗,贺永宁,赵小龙 ,樊瑞睿 ,4†

(1. 散裂中子源科学中心,广东东莞 523803;2. 西安交通大学 微电子学院,西安 710049;3. 中国科学院 高能物理研究所;4. 粒子探测与电子学国家重点实验室: 北京 100049)

中子能谱是指中子数随能量的变化,在表征中子与物质相互作用中具有重大意义。目前,中子能谱的测试主要依赖飞行时间法[1]、有机闪烁体测试法[2-3]、多球谱仪法[4]及多箔活化法等[5]。飞行时间法主要依靠确定中子的飞行时间获得中子的能量,后得到中子能谱。有机闪烁体测试法、多球谱仪法及多箔活化法等都是通过探测器对不同能量中子的不同响应,逆推间接获得中子能谱。以多球谱仪为例,中子慢化材料的外壳会改变入射到内部中子热敏探测器表面的中子能谱,从而改变每个Bonner球的通量响应,并通过建立方程矩阵,使用最大熵法、遗传算法及蒙特卡罗模拟等求解该方程获得中子的能谱信息[6-8]。类似Bonner球的测试原理,本文提出了一种利用静态随机存取存储器(static random access memories,SRAM)的单粒子翻转截面信息测量求解低能段中子能谱的方法。与传统的中子能谱测量方法相比,该方法具有成本低、操作方便及数据处理方便等优点。基于近些年对低能加速器中子源、裂变中子源和硼中子俘获治疗中子源(boron neutron capture therapy ,BNCT)等低能中子源的中子能谱测量需求不断增加,该方法具有很大的发展潜力[9-10]。

作为一种半导体存储设备,存储在SRAM中的数据只要通电就可连续保存。单粒子翻转 (single event upset, SEU)是指在存储设备中因重离子、质子和中子等粒子入射导致存储器内数据发生翻转的现象。以中子为例,由于中子和器件碰撞后产生二次带电粒子,在半导体中产生电子-空穴对,当电极收集的电荷量大于临界电荷时,就会发生SEU。一般认为,SRAM的SEU截面与半导体工艺和器件设计密切相关,不同公司、不同型号的SRAM对中子有不同的响应函数,可根据SRAM的翻转截面和被辐照后的翻转次数建立方程组,用于求解中子能谱。国内外已有很多通过单能中子源测试SRAM的翻转截面的工作,基于这些工作,可利用已知翻转截面的SRAM进行中子能谱求解工作[11-16]。

本文基于Lambert等[11]在单能中子源测试的7个SRAM的翻转截面曲线,得到类似Bonner球对中子的响应函数,并通过求解根据SRAM翻转截面和翻转次数建立的矩阵方程获得中子能谱信息。采用235U裂变中子谱和中国散裂中子源Back-n白光中子束谱进行计算[1, 17]。并采用奇异值分解(singular value decomposition, SVD)进行解谱。

1 解谱方法介绍

不同工艺、不同型号的SRAM,翻转截面不同,即对不同能量中子的响应不同。因此被中子辐照时,不同型号SRAM的翻转率也不同。结合已知的SRAM的翻转截面信息,可将SRAM的翻转率表示为SRAM翻转截面和中子能谱的矩阵乘法。利用可SVD方法对这个矩阵方程求解获得中子能谱信息。SVD是线性代数中的一种矩阵分解,是对可逆矩阵特征值分解对任意矩阵的一种推广[18]。 图1为能谱测试的具体流程。

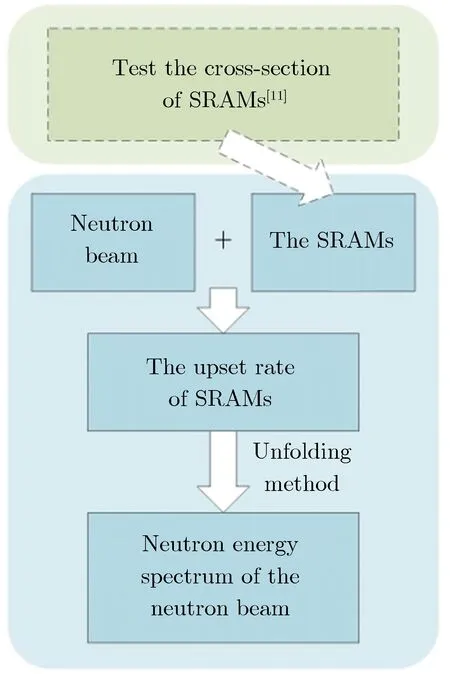
图1 能谱测试的具体流程Fig.1 Specific process of energy spectrum testing

SRAM的翻转率可用矩阵方程表示为

N=R·F

(1)

其中:N为k列矩阵,表示第k个SRAM的翻转率;R为i行k列矩阵,表示第k个SRAM对第i个能量bin内的中子的响应;需求解的F为i行矩阵,表示每个能量bin内的中子数。求解时需先对R进行奇异值分解

R=U·S·VT

(2)

其中:R为k阶的正交矩阵;V为i阶的正交矩阵;S的对角线元素是R的奇异值;其他元素为0。由于矩阵R是不可逆的,所以SVD法通过求矩阵R的伪逆来求解矩阵方程,然后就可得到与矩阵F的欧式距离最小的近似解[19]。则每个能量bin内的中子数F可表示为

F=R+·N=V·S+·UT·N

(3)

2 SRAM翻转率的计算

图2和图3分别为计算中使用的235U裂变中子谱及中子引起的SRAM单粒子位翻转截面。

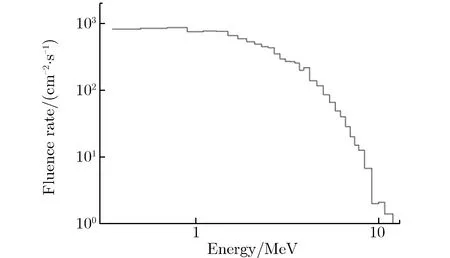
图2 计算中使用的235U裂变中子谱Fig.2 The fission neutron spectrum of 235U for calculation

图3 中子引起的SRAM单粒子位翻转截面Fig.3 SEU cross section of the SRAMs induced by neutrons

根据Lambert等[11]之前的工作,SRAM的单粒子位翻转截面可用图3所示的4参数Weibull函数进行拟合,表示为

(4)

其中:σsat为饱和截面;Eth为中子的阈值能量;α和β为Weibull分布的形状因子。Lambert等[11]已通过单能中子源测试拟合了7种不同的SRAM的翻转截面,被测器件单粒子位翻转截面的Weibull函数参数如表1所列。

由图3可见,SRAM的敏感区基本位于1～10 MeV,能量小于1 MeV的中子,因能量太小,基本不会在SRAM内导致翻转,当能量大于10 MeV时,中子引起的翻转往往表现出饱和特性。因此,基于SRAM的单粒子效应测试中子能谱更适用于对低能中子源的能谱测试。

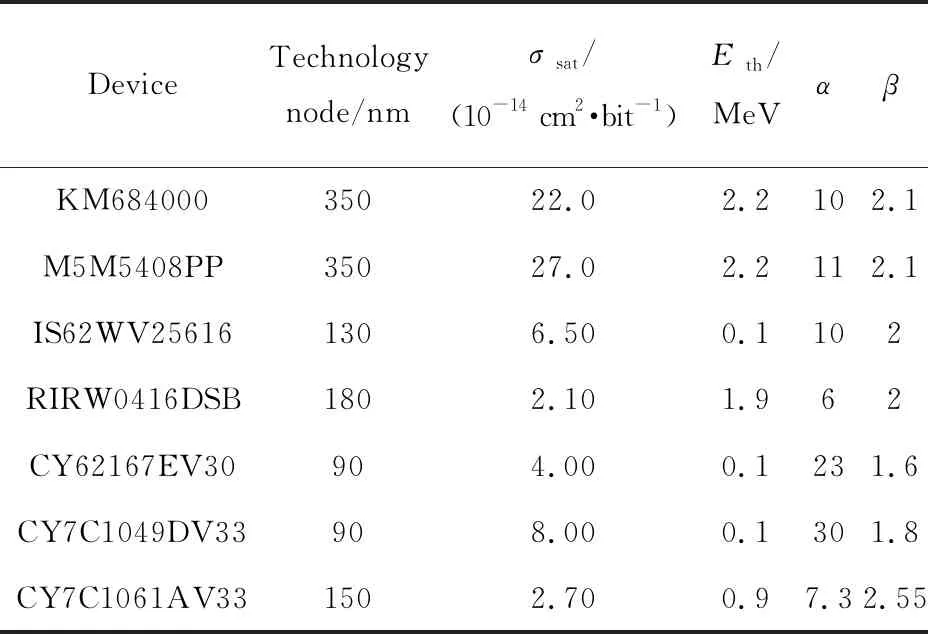
表1 被测器件的单粒子位翻转截面的Weibull函数参数[11]Tab.1 Weibull parameters of the SEU cross-sections for the tested devices[11]

首先尝试对235U的裂变中子谱进行解谱[17]。根据中子能谱的能量bin信息带入式(4),可得到该SRAM对于每个能量bin内的中子的响应函数,以此计算每个SRAM的翻转率。其中,能量bin的索引为i,不同 SRAM的索引为k。则第k个SRAM的翻转率可表示为

Nk=∑Rkifi

(5)

其中:Nk为第k个SRAM的翻转率;Rki为第k个SRAM对能量位于第i个能量bin内的中子的响应;fi为能量位于第i个能量bin内的中子数。据此,根据调研得到的7个SRAM的翻转截面和235U的裂变中子能谱,计算SRAM 被235U裂变中子源辐照后的翻转率,如表2所列。

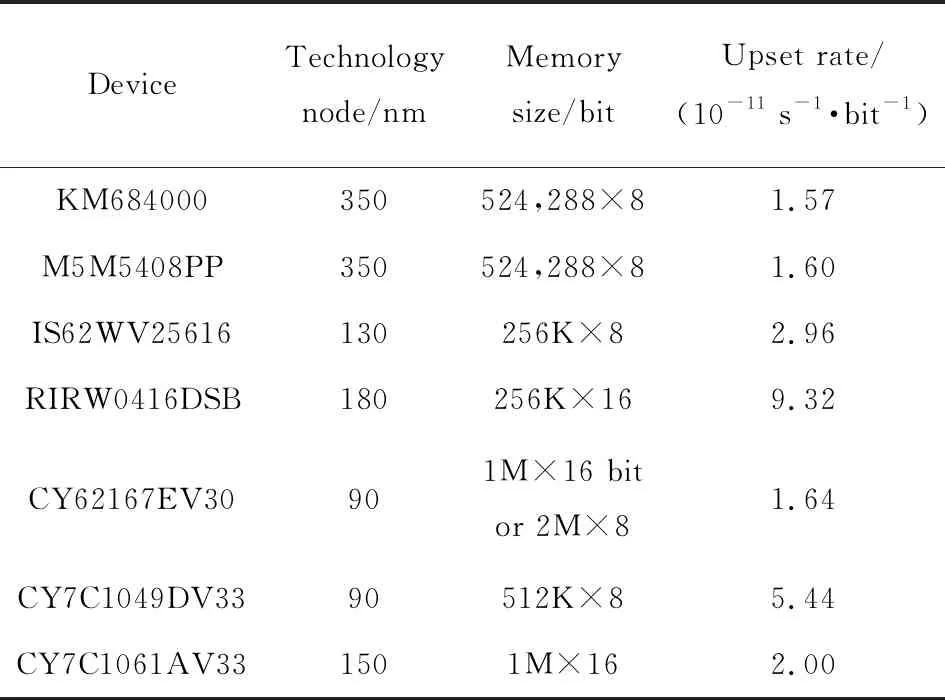
表2 SRAM被235U裂变中子源辐照后下的翻转率Tab.2 The upset rate of SRAM under the fission neutron spectrum of 235U

3 解谱结果和分析

3.1 已知SRAM的中子能谱解谱结果

第2节已计算了每个SRAM的翻转率。但由图3可见,在低能区和高能区,SRAM截面为0或饱和,而235U裂变中子谱能量范围约为0.35～12 MeV,正好位于这些SRAM的敏感区。将235U裂变中子谱被分为34个能量bin,采用式(3)对中子能谱进行反解,得到235U裂变中子谱解谱结果和相对偏差,如图4所示。

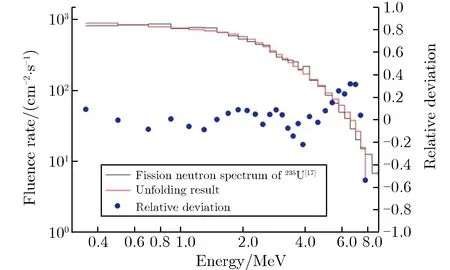
图4 235U裂变中子谱解谱结果和相对偏差Fig.4 The fission neutron spectrum of 235U unfolding result and the relative deviation

为进一步研究解谱的准确性,将每个能量bin内的相对偏差表示为

(6)

其中:Ni′ 和Ni分别为第i个能量bin内通过解谱得到的中子数和原能谱中子数。由图4解谱结果可见,每个能量bin内的相对偏差基本都小于20%,可认为该解谱方法是可行的。

验证该解谱方法后,采用该方法对中国散裂中子源反角白光中子束线进行解谱。反角白光中子的能谱峰值约为1 MeV,能谱相对较宽,为0.5 eV ～ 200 MeV,能谱如图5所示。

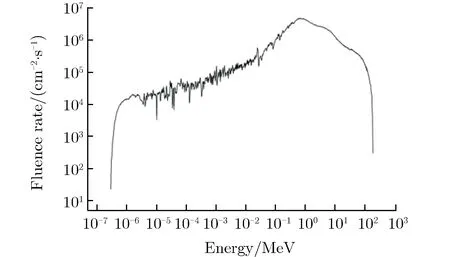
图5 中国散裂中子源白光中子谱Fig.5 CSNS Back-n white neutron spectrum

在解谱过程中,将整个能谱划分为55个能量bin。由于反角白光中子的能谱范围大于SRAM单粒子效应的能量敏感区,因此解谱方法只适用于反角白光中子谱的一部分,即 1 ～ 10 MeV能量范围内的SRAM敏感区。同样采用式(3)对中子能谱进行反解,得到中国散裂中子源白光中子能谱解谱结果和相对偏差如图6所示。

图6 中国散裂中子源白光中子能谱解谱结果和相对偏差Fig.6 CSNS Back-n white neutron spectrum unfolding results and the relative deviation

由图4和图6可见,235U裂变中子谱的展开结果比散裂中子源白光中子束线的能谱展开结果更准确。主要考虑因为235U裂变中子能谱更贴近SRAM的敏感区,另一方面,235U裂变中子谱的能量bin数目更少,因此,考虑随着SRAM数量的增加,解谱结果会更加准确。

3.2 参与解谱的SRAM个数与解谱结果准确度分析

考虑解谱结果可能与参与解谱的不同型号的SRAM个数有关,在这一部分,除了上述Lambert等[11]测试的7个SRAM外,另外调研了Cecchetto 等[15]和Roeed 等[16]测试的5个SRAM的翻转截面信息,重新进行解谱工作。新加入解谱工作的器件的Weibull分布参数如表3所列。

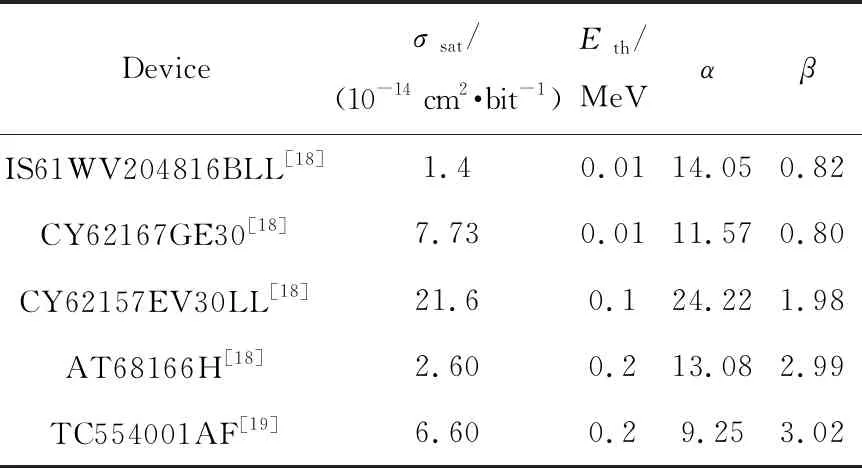
表3 新加入解谱工作的器件SEU截面的Weibull分布参数Tab.3 Weibull parameters of the SEU cross sections for the added devices

同样根据上述方法进行解谱,12个SRAM的翻转截面如图7所示,增加SRAM器件后的解谱结果如图8所示。

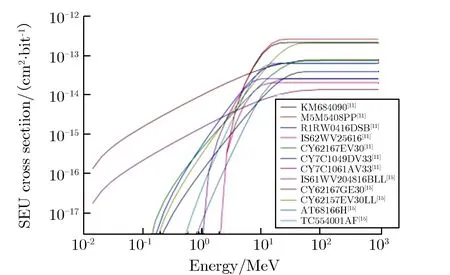
图7 12个SRAM的单粒子位翻转截面Fig.7 SEU cross section of the 12 SRAMs

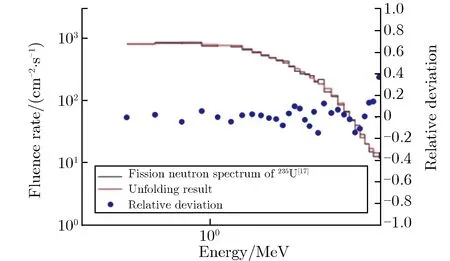
(a) The 235U fission neutron spectrum unfolding resultss and the relative deviation

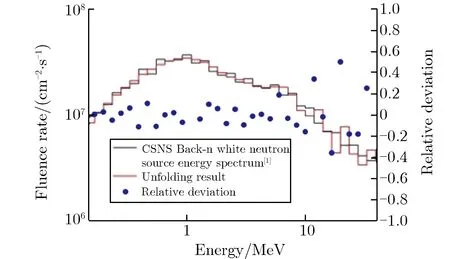
(b) CSNS Back-n white neutron spectrum unfolding result and the relative deviation图8 12个SRAM器件的解谱结果Fig.8 Upset cross section of the 12 SRAMs

由图8可见,12个SRAM参与解谱的结果比图4和图6给出的7个SRAM参与的解谱结果更接近原始中子能谱。为进一步评价整个解谱结果的准确性,选用交叉熵来描述解谱结果与原始谱的差异大小。已知两个分布函数p(x)和q(x),则这两个分布的交叉熵定义为[20]

(7)

由式(7)可知,交叉熵|SCE| 提供了将分布q(x)修改为p(x)的信息量的一个量度,即判断q(x)与p(x)之间的差异。图9为解谱结果的交叉熵随SRAM个数的变化关系。

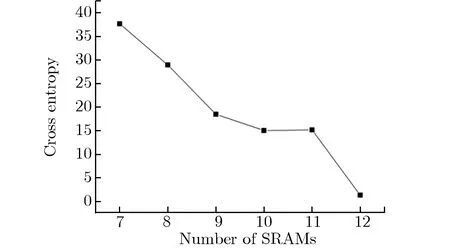
(a) 235U fission neutron spectrum

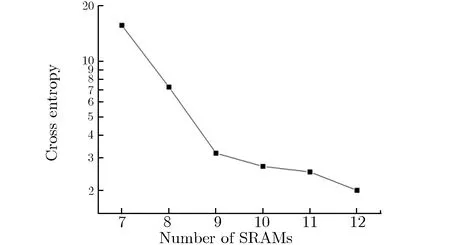
(b) CSNS Back-n white neutron spectrum图9 解谱结果的交叉熵随SRAM个数的变化关系Fig.9 Cross entropy vs. the number of SRAMs

在图9可见,随着SRAM数目的增加,解谱结果与原中子能谱的交叉熵的绝对值均减小,说明随着更多不同型号的SRAM参与解谱,解谱结果越准确,与上述推测一致。故此,为获得更准确的未知中子能谱的信息,需已知更多不同型号的SRAM单粒子翻转截面。

4 总结

本文验证了采用SRAM测量中子能谱的理论可行性,计算了不同SRAM数量与能谱展开结果之间的关系。根据计算,主要限制因素是SRAM的数量和SRAM的敏感区域大小。为获得更多的已知翻转截面的SRAM器件,本文提出了一种基于白光中子源的操作方便的SRAM翻转截面测试方法,并计算验证了该方法的可行性。考虑准确测试宽能量范围的中子能谱的需求,需获得敏感区更宽,对中子响应概率更高的SRAM器件。