基于多模型的铁路货运量预测对比
2023-10-20燕学博福建理工大学福建福州350118
燕学博,曹 雨(福建理工大学,福建 福州 350118)
0 引言
铁路货运量是我国物流的重要组成部分,也是衡量铁路货运发展水平和能力的重要指标。近年来,由于国内经济社会的发展以及我国城市化步伐的加速,城市居民对各种商品的需求量不断增加,这导致了铁路货运量呈逐年递增的趋势。为了满足社会对货运服务的需求,进一步提高铁路货运服务质量,加强对铁路货运组织建设和发展战略的研究,对铁路货运量的精准预测十分必要。传统的货运量预测模型主要包含统计模型预测法、神经网络预测法以及组合模型预测法。
黄雪婷[1]分别对比了SARIMA 模型、LSTM 模型与组合模型的预估数据,结果表明,组合模型无论在较短周期还是在较长周期的预估上,表现结果均强于单一模型;张冠东等[2]改进了传统LSTM 模型,提出一种多维度LSTM 模型,并分别对铁路、公路、航空货运量进行预估,结果表明多维LSTM 模型预测效果优于传统LSTM 模型;贾春苗等[3]采用ARIMA 与多元回归模型相结合的综合模型对陕甘铁路货运量进行了预估,结果显示,复合模型的预测效果优于传统单一模型;冉叶子[4]利用ANN 与LSTM 深度学习模型对贵州省货运量进行预测,并与传统时间序列预测法ARIMA 进行比较,结果表明深度学习模型预测效果优于传统模型;杨飞[5]采用了Logit 加权方法,将BP 神经网络、霍尔线特性趋势指数平滑算法与ARIMA 相结合构建了全新的组合模型,将该模型与基于等权分配法的组合模型加以比较,结果表明采用Logit 加权方式的组合模型表现效果明显高于采用等权分配的组合模型;周昌野等[6]基于网格搜索算法对LSTM 模型进行改良,得出全新的GS-LSTM 模型,实验结果表明,经过改良的GS-LSTM 模型泛化能力要强于传统LSTM 模型。
以上研究表明,组合模型的泛化能力要强于单一模型,而对组合模型的权重分配法中,等权分配法表现较差。组合模型中能够更好实现对单一模型的优点整合,特别是强化数据预测中线性部分与非线性部分的有机结合。本文以国家统计局公布的2005 至2022 年全国铁路货运量为例,分别利用传统ARIMA 模型,深度学习中LSTM 模型与二者相结合的ARIMA-LSTM 组合模型对数据进行拟合,选取最优预测方案。
1 模型理论综述
1.1 ARIMA 模型
ARIMA (p,d,q)模型是经过差分处理的AR(p)模型与MA(q)模型的组合,它包含三个方面,分别为自回归函数AR,函数阶数I 与移动平均函数MA,其中参数p,q 分别表示自回归函数与移动平均函数阶数,d 代表差分次数,ARIMA (p,d,q)模型基本公式为:
式中:yt与yt-i分别代表预测值与历史值;μ 为白噪声项;γi与θi分别代表自相关系数与误差项系数;p 与q 分别代表自回归阶数和移动平均阶数;εt与εt-i代表模型的误差和时间点i 之间的偏差。
ARIMA (p,d,q)模型步骤包括数据平稳性检测、模型定阶、模型选取、白噪声检验等,具体流程如图1 所示。
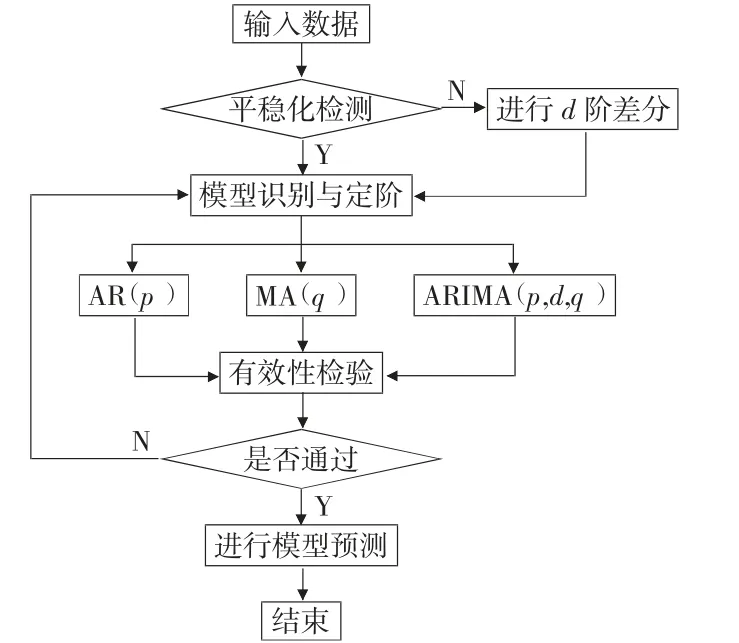
图1 ARIMA 模型预测流程图
1.2 LSTM 模型
长短时记忆网络(Long Short Term Memory Network,LSTM)模型是由Schmidhuber 和Hochreiter 于1997 年提出,它的基本原理为循环神经网络(Recurrent Neural Network,RNN)模型,它针对传统RNN 模型中经常出现的梯度消失,长时训练信息无法保留等问题进行优化,在此基础上首次引入“门”的概念,使每一个神经元同时具有输入门、遗忘门和输出门。LSTM 模型基本工作原理如图2 所示,
模型中ft、it、Ot分别代表遗忘门、输入门和输出门,Ct代表细胞更新状态,ht代表当前时刻输出值,σ、tanh 均为激活函数,其中:σ 采取Sigmoid 激活函数,tanh 则采用正切激活函数。遗忘门、输入门、输出门、细胞更新状态、当前节点输出计算方式分别如下:
其中:Wf、Wt、Wo、Wc、bf、bi、bo、bc依次代表遗忘门、输入门、输出门和细胞更新状态的时间权重及其偏置项,ht-1表示上一时刻隐藏层的向量,Xt则代表当前时刻输入。
1.3 组合模型
组合模型可以解决单一预测模型的不足,进一步提升预测的精度,组合模型通常采取串联、并联两种模式,其具体流程如图3、图4 所示:
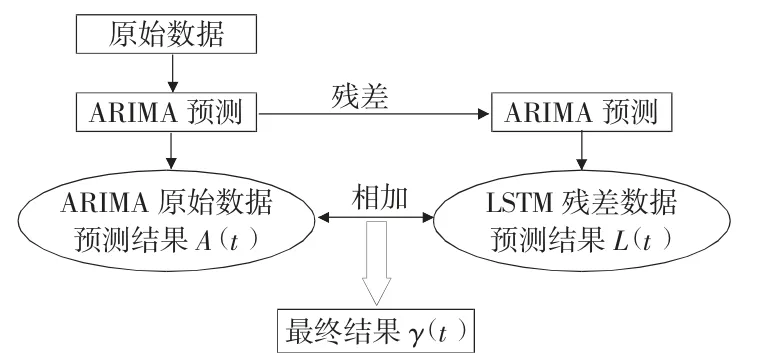
图3 串联模型流程图
2 数据处理与评价指标选取
2.1 数据处理
本文数据来源均为国家统计局公布数据,实验软件分别为SPSS Statistics 20.0 与Matlab 2018b。为保证实验准确性,ARIMA模型采用SPSS 中专家建模的结论,最终模型为ARIMA (0,1,0)(0,1,1);LSTM 模型选用单隐层模型,隐层节点数为70,优化器为Adam,最大循环次数为300,初始学习率为0.01。
2.2 评价指标选取
为量化评估模型精度,本文选取平均绝对误差(Mean Absolute Error,MAE)指标,平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)指标,均方误差(Mean Square Error,MSE)指标和均方根误差(Root Mean Square Error,RMSE)指标作为评估依据,指标计算公式如下:
其中:Yi为i 时刻实际值,为i 时刻模型预测值,n 代表样本个数。
3 实证分析
3.1 串联耦合模型应用
串联模型中,首先通过ARIMA 模型对原始数据进行估计判断,得出预测结果A(t);而后通过LSTM 模型对ARIMA 模型预测中出现的残差项进行预测,并得出预测结果L(t),串联模型最终预测结果Y(t)为:
对比单一模型与串联耦合模型下的MAE、MAPE、MSE、RMSE 指标,对比结果如表1 所示。通过对比可以得出结论,组合模型各项指标值均低于单一模型,表明组合模型的泛化能力明显强于单一模型。

表1 单一模型与组合模型对比结果
3.2 并联耦合模型应用
并联组合模型基本方法是分别利用各模型对原始序列进行预测,而后确定单一模型所占权重Wi、Wj,基本运算如下:
当前多模型权重确定方法包括算术平均法、方差倒数法、均方倒数法、简单加权法和熵权法。本文对各权重方法产生的组合模型进行比较,选取最优组合作为并联组合模型解。
3.2.1 算术平均法
算术平均法通常也叫做等权平均法,即对各模型均赋予相同权重,权重确定公式为:
其中:Wi为第i 个模型权重,I 为模型总数。
3.2.2 方差倒数法
方差倒数法是对算术平均法的改进,以预测误差的平方和作为权重确定依据,基本公式为:
式中:Di为误差平方和,其基本公式为:
式中:xt为真实值,为模型的预测值。
3.2.3 均方倒数法
均方倒数法是对方差倒数法的改进,体现在单一模型的误差平方和越大,所属模型在组合模型中权重越小,其基本公式为:
式中:Di定义与方差倒数法Di定义相同。
3.2.4 简单加权法
简单加权法确定权重方法是先将各模型预测误差的方差之和进行排序,排名越靠前的预测模型,其组合模型中加权系数越小,计算公式为:
3.2.5 熵权法
熵权法是通过衡量指标变异性的能力来判断客观权重。熵权法认为,某指标信息熵越小,则表明指标变异程度大,所能反映的信息量越多,因此其相对权值越大,熵权法基本运算公式为:
式中:1-ej代表信息效用,ej代表第j 个指标的信息熵,其计算公式为:
对比结果显示,采用方差倒数法确定权重的并联模型为最优组合模型,且所有指标均小于其他模型,表明了该模型泛化能力及预测精准度较其余模型更佳。不同方法所确定组合模型权重及精度对比如表2、表3 所示:

表2 组合模型权重表

表3 多模型预测精度对比表
4 模型评价
分别对比ARIMA 模型、LSTM 模型以及ARIMA-LSTM 组合模型的参数,最终选定基于方差倒数的组合模型为最优模型。对各模型的预测值与原始数据进行拟合,可以明显看出组合模型的拟合效果要好于单个模型,如图5 所示。
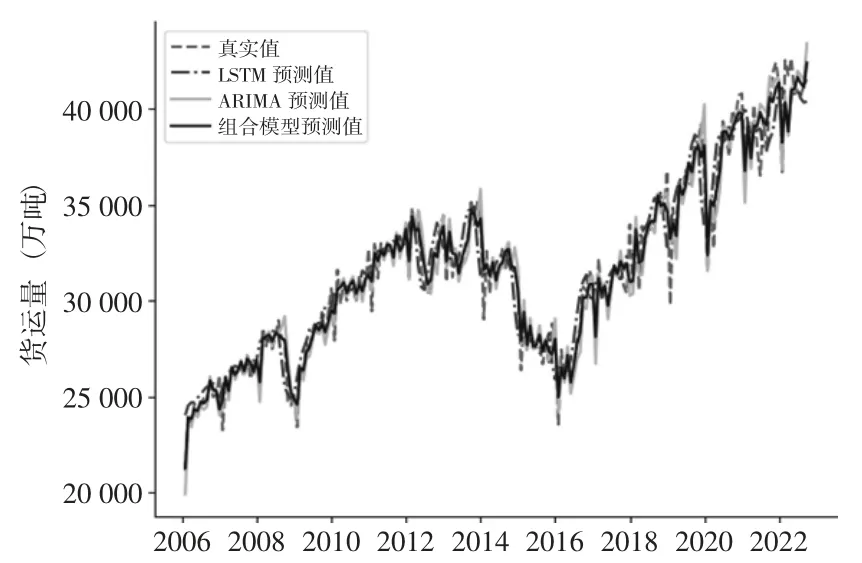
图5 多模型数据拟合图
图6 为各模型与真实数据的绝对误差值。由图6 可以清晰看到组合模型误差波动整体较单一模型要小,其绝对误差值也低于单一模型,表明ARIMA-LSTM 组合模型的稳定性及误差较单一模型表现较好。
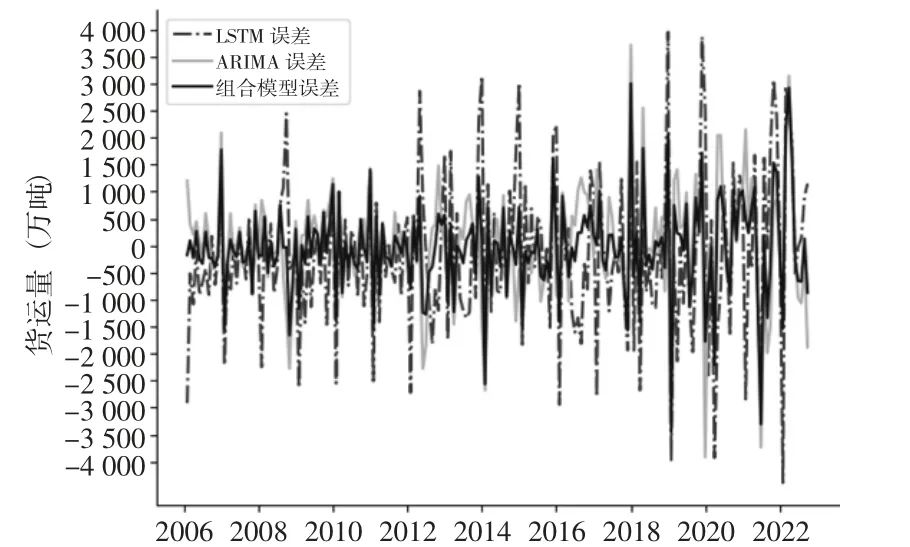
图6 多模型绝对误差对比
为进一步量化参数,对各模型预测效果进行评价,分别对比各模型MAE、MAPE、MSE、RMSE 指标,结果如表4 所示。通过对比可得,组合模型较ARIMA 模型的MAE、MAPE、MSE、RMSE 指标分别降低15.26%、15.62%、24.64%、17.12%,较LSTM 模型分别降低25.32%、32.67%、43.66%、28.33%。

表4 多模型指标对比
5 研究结论
本文以全国2005 年1 月至2022 年10 月铁路货运量为研究目标,并分别采用ARIMA 模型、LSTM 模型与ARIMA-LSTM 组合模型对原数据进行预测,在组合模型中,采用ARIMA 模型与LSTM 预测残差所共同构建的串联模型,以及采用算数平均法、方差倒数法、均方倒数法、简单加权法、熵权法构建的并联模型,并以MAE、MAPE、MSE、RMSE 指标作为评价模型依据,研究结论表明:(1)任意组合模型拟合效果均强于单一模型。(2)组合模型中采取不同的权重赋予方式会导致组合模型预测精度不同,通过对比五种权重确定方式,以方差倒数法确定的权重组合模型表现最佳。(3)铁路货运量数据兼具线性与非线性特征,在时间维度原始数据包含趋势性与季节性特征,单一线性模型预测效果较差,在对以上数据进行预测时应兼顾线性与非线性特征,采取线性与非线性相组合模型对该数据进行预测。
