关于《数学通报》中的一个问题的探究

司志本 罗 晋

(河北民族师范学院教师教育学院 067000)

《数学通报》2012年第9期“数学问题解答”栏目中的第2078题(以下简称原题)为：

已知正实数x、y满足x7+y7=x3+y3，求证：x4+y4≤2.

原题从x、y的对称性和指数间的和谐性(7=3+4)两个方面，体现了数学的形式美.对原题的结论作进一步的探究推广后，可以更深入体会对称性、和谐性的数学美.

1 初步推广

先把原题x7+y7、x3+y3和x4+y4中x、y的指数之间“7=3+4”这个关系推广到一般的情况.即有下面的命题1.

命题1若正实数x、y满足

xm+n+ym+n=xn+yn，

(1)

则

xm+ym≤2.

(2)

其中m和n都是正整数.

证明当x、y中有一个是1时，不妨假设x=1，则根据(1)式可得ym+n=yn，从而有ym=1，注意到x、y都是正实数，所以有y=1，从而有xm+ym=2，此时(2)式显然成立；

当x、y都不是1时，根据命题中x、y的对称性，不妨假设x≥y.把(1)式进行移项得到

xm+n+xn=yn+ym+n.

整理得

xn(xm-1)=yn(1-ym)，

即

(3)

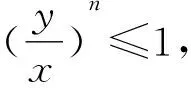
(xm-1)≤(1-ym)，

即

xm+ym≤2.

2 进一步推广

由命题1，当x、y都是1时，xm+ym=2；当x、y都不是1时，除了(2)式成立以外，还有下面的命题2和命题3成立.

命题2满足

xm+n+ym+n=xn+yn，

(1)

的正实数x、y，如果不全为1，那么必有一个大于1，一个小于1.

证明如命题1的证明，(3)式中xm-1与1-ym是同号的，因此xm>1当且仅当1>ym，即x>1当且仅当1>y.同样x<1当且仅当1

把命题2推广到多个正实数，得到下面的命题3.

命题3若正实数x1，x2，…，xt满足

(4)

则xi(i=1，2，…，t)不可能同时大于1，也不可能同时小于1.

事实上，把(4)式的右端移到左端，整理可得

(5)

由(5)式可知，xi(i=1，2，…，t)不可能同时大于1，也不可能同时小于1.

3 最终结论

把命题1推广到多个正实数，得到下面的命题4.

命题4若正实数x1，x2，…，xt满足

(6)

则

(7)

证明当x1=x2=…=xt=1时，(7)式显然成立.不妨假设x1，x2，…，xt不全为1，即可设x1≥x2≥…≥xi≥1≥xi+1≥…≥xt.

要证明(7)式成立，只要证明

(8)

成立即可.

由(6)式可得

从而有

(9)

将(9)式代入(8)左端，则有

(10)

因为，x1≥x2≥…≥xi≥1≥xi+1≥…≥xt，所以有，

(11)

(12)

(13)

(14)

由(11)—(14)式可知，(10)式右端的每一项的两个因式都是一正一负(或者是0)，也就是说，(10)式右端的每一项都是负数(或者是0)，所以(8)式成立.