叶片弯、扭、掠造型规律对透平级气动性能的影响
2023-10-18邱庆辉付亚玮黄典贵
邱庆辉, 付亚玮, 李 博, 黄典贵
(上海理工大学 能源与动力工程学院,上海 200093)
叶片作为透平中的能量转换装置,其三维造型对透平的气动性能有重要影响。随着计算机的发展,透平全三维优化设计方法逐渐进入学者视野,而弯、扭、掠叶片技术作为提高透平效率、改善透平气动性能的重要手段,得到了广泛的研究与应用。
20世纪60年代,Filippov等[1]提出了一种新的叶片成型方法——叶片弯扭联合气动成型,可以使叶栅中的能量损失下降30%~50%。黄影虹等[2]通过所开发的弯扭叶片程序发现弯扭叶片能有效改善叶栅流道内的流动情况。邹正平等[3]从叶片气动负荷分布角度入手,通过解析方法对叶片三维造型中各参数的位势影响进行模拟与分析。陈波等[4]利用NURBS对叶片截面和积叠线进行弯、倾、扭、掠参数化改型,优化结果表明叶片能量损失降低了0.85%。Karrabi等[5]研究了扭曲、倾斜和弯曲叶片对汉诺威轴流透平性能的影响,结果表明扭曲叶片的影响更显著。
众多学者在维持动叶一定扭转规律的前提下,研究了静叶片的弯、扭、掠不同改型对透平气动性能的影响[6-10]。然而静叶片造型改变后,其出口处的流场也会发生变化,势必导致动叶来流条件的变化。对处于最佳匹配状态的动、静叶而言,静叶或动叶的单独改型会使透平级的气动性能下降。因此,对静叶进行不同程度的弯、扭、掠改型时应寻求与其相互匹配的动叶扭转规律,这样才能使得透平的性能得到最大的提升。
笔者基于动、静叶的最佳匹配原则对叶片进行参数化改型:利用正交优化方法,对静叶进行弯、扭、掠改型时也对动叶进行扭改型,使得改型后动、静叶处于新的相互匹配状态。通过流场分析研究叶片弯、扭、掠造型规律对透平级气动性能的影响,为后续的耦合造型规律研究提供重要参考。
1 计算模型与方法
1.1 研究对象
本文研究对象为某高压透平首级[11],为排除该级静叶弯扭因素和端壁型线的影响,对原始静叶进行消弯、消扭改型,对原始动叶进行延伸。改型后得到叶高均为80 mm的等高直静叶和等高扭动叶,且均为轴对称端壁。对改型后的动叶进行扭转优化,使之与等高直静叶处于最佳匹配状态,此时透平级总总效率为92.49%,将该级作为本文的初始透平级进行研究,其初始直静叶和初始扭动叶如图1所示。最终所得透平的转速为8 279 r/min,静叶叶片数为46,动叶叶片数为76。

图1 初始直静叶和初始扭动叶
1.2 网格划分及边界条件
本文数值模拟采用稳态雷诺时均方法,湍流模型选择SST模型,近壁面第一层网格高度为1.0×10-6m,y+≤1。进口总温为709 K,总压为344 740Pa,出口平均静压为149 800 Pa,动叶叶顶间隙为0.4 mm。计算域入口距静叶前缘2倍静叶轴向弦长,出口距动叶尾缘3倍静叶轴向弦长,计算域网格采用O4H型拓扑结构,网格划分细节如图2所示。

图2 三维网格划分
选取3套网格对透平进行数值模拟,网格具体参数如表1所示。综合结果的稳定性与计算成本,选择第2套网格作为后续计算的网格规模。

表1 不同网格的具体参数
1.3 参数化造型方法
借助三维建模软件对叶片进行参数化建模和弯、掠改型。选取多个截面,采用重心积叠的形式构建三维叶片,弯曲积叠线和掠积叠线参数化控制方法分别如图3和图4所示,其中参数化控制点1、6分别与叶片根部截面、顶部截面叶型的重心重合,控制点2、3、4、5处于点2、点5的连线上,α1、α2、α3分别表示参数化控制点2、4、5与展向的夹角,P1×C1、C1分别表示控制点2、3距根部的相对高度,C2、P2×C2分别表示控制点4、5距顶部的相对高度。本文中规定:静叶压力面与端壁的夹角≤90°为正弯,反之为反弯;叶片在轴向上朝来流方向偏移为前掠,反之为后掠。

图3 弯造型参数化控制方法
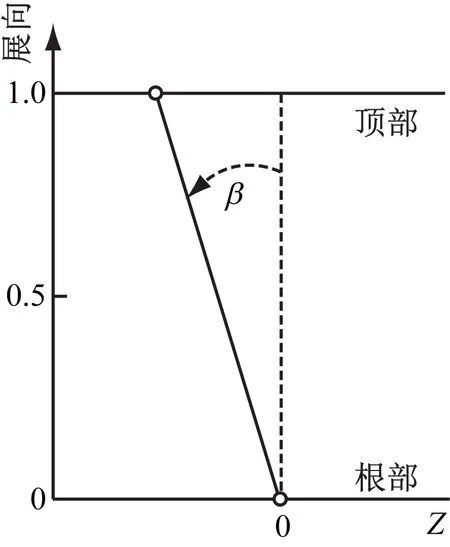
图4 掠造型参数化控制方法
使用自编程序对叶片进行扭转改型,如图5所示。均匀选取多个截面,每个截面绕其质心旋转过的角度为该截面的扭角y,不同叶高截面的扭角满足y=kx+b,k、b为扭角的参数化变量,逆时针旋转时扭角为正,称为正扭,反之为反扭;x的取值采用线性插值的方法,叶根处的值为0,叶顶处的值为2。弯、扭、掠参数化造型所涉及的影响因子如表2所示,其中C1、C2、P1、P2、α1、α3控制静叶弯造型,k1、b1控制静叶扭造型,k2、b2控制动叶扭造型,参数β控制静叶掠造型。

表2 弯、扭、掠参数化造型控制变量

图5 扭造型控制方法
2 计算结果与分析
透平叶片的三维造型对其内部的流场结构有重要影响,为了改善流场结构,减小流动损失,提升透平的性能,本节对初始透平叶片进行弯、扭、掠造型优化并分析不同造型对透平流场的影响。静叶、动叶出口总压损失系数ω的定义[12]为:
(1)

2.1 弯造型的应用
以静叶弯造型的6个影响因子和动叶扭造型的2个影响因子为自变量,以透平总总效率为因变量,设计了49组正交优化试验,其中各因子水平的取值如表3所示。正交优化后所得最佳总静效率和总总效率分别提升了0.22百分点和0.29百分点,弯静叶匹配优化后的扭动叶的总总效率高于静叶单独弯曲优化,对比结果如表4所示。表5为利用极差分析法得到的静叶弯曲与动叶扭转各因子最佳取值,此时静叶正弯,动叶正扭且扭角沿展向增大。

表3 弯造型影响因子水平取值

表4 弯静叶匹配扭动叶的正交优化结果

表5 静叶弯曲与动叶扭转各因子的最佳取值
图6为弯造型静叶吸力面径向压力梯度分布图,深色区域表征叶片表面存在由叶顶指向叶根方向的正压力梯度,浅色区域表征的压力梯度方向则相反。如图6(a)所示,原始静叶吸力面前缘至30%弦长区域主要为负压力梯度区域,沿展向负压力梯度区域减小;30%弦长至尾缘区域主要为正压力梯度区域,且在叶顶存在2个压力梯度掺混的区域,说明流体流经该区域时会出现径向上的碰撞并伴随着能量的消耗。如图6(b)和图6(c)所示,弯静叶叶顶前缘正压力梯度明显变大,有利于叶顶端区的低能流体逐渐向下迁移,以至于在靠近叶顶区域形成一段径向压力梯度为0 kg/(m2·s2)的流动区域,且叶片中部径向压力梯度为0 kg/(m2·s2)的区域明显变大,有利于减弱叶片中部通道内的二次流强度。

(a) case 1静叶
图7为弯造型静叶出口熵增沿展向的分布图。如图7(a)所示,由叶顶至叶根方向,原始静叶出口熵增逐渐增大,且集中在静叶尾迹区,这是尾迹区低速流体与通道内高速主流、端区边界层低能流体相互掺混的结果。如图7(b)和图7(c)所示,弯静叶出口熵增主要集中在叶顶、叶根尾迹区,在出口中部区域熵增比原始静叶小,尤其在15%~50%叶高处,表明弯静叶出口中部区域的混乱程度有所减弱。

(a) case 1静叶
图8为弯造型静叶所匹配的动叶通道内以及出口处的熵增沿展向的分布图。如图8(a)所示,原始动叶的熵增主要集中在叶顶区域且沿着下游逐渐增大,这是叶顶泄漏流与吸力面侧主流、叶片上部通道涡相互掺混向下游发展并与动叶尾迹流相互干扰的结果;叶片下部的熵增也较为明显,这是叶片下部通道涡沿着下游逐渐发展并在出口处与动叶尾迹流相互干扰的结果。如图8(b)所示,弯静叶所匹配的初始动叶顶部熵增较图8(a)所示动叶变化不大,而在叶根至80%叶高区域,熵增大于520 J/(kg·K)的面积明显变大,且动叶出口沿展向的熵增有所增大,表明该动叶内的流动损失较大。如图8(c)所示,弯静叶所匹配的优化动叶顶部熵增较图8(a)所示动叶略有减小,而在叶片下部的熵增削弱较为明显,表明优化后的动叶内流动损失较小,这也是其效率升高的原因。

(a) case 1动叶
图9为弯造型静叶、动叶出口总压损失系数沿展向的分布图。对于静叶出口,case 1的原始静叶总压损失系数均值为0.057 0,在靠近叶根、叶顶区域由于受到端区二次流的影响,总压损失系数明显增大;在10%~80%叶高处,总压损失系数沿展向递减,而在叶片上部由于径向二次流的影响,总压损失系数较大,呈现先增后减的趋势。case 2和case 3的弯静叶总压损失系数均值分别为0.055 6和0.055 9,相较case 1分别减小2.46%和1.93%;叶片中部总压损失系数比较均匀,在60%叶高以下,弯静叶总压损失较原始静叶小,而在60%叶高以上,弯静叶的总压损失有所增大。
对于动叶出口,case 1的原始动叶总压损失系数均值为0.236,叶片下部由于受到下部通道涡的影响,总压损失系数较大;叶片上部在上部通道涡以及叶顶泄漏涡的双重影响下,总压损失系数明显增大,而在叶片中部总压损失系数比较均匀。case 2和case 3的叶片总压损失系数均值分别为0.252和0.231,相较case 1分别增大6.78%和减小2.12%;叶片上部总压损失系数较原始动叶变化不大;而在65%叶高以下,case 2的动叶总压损失比原始动叶大,case 3的动叶总压损失比原始动叶小,case 1~case 3的动叶总压损失沿展向的变化趋势基本一致。
2.2 扭造型的应用
以静叶扭造型的2个影响因子和动叶扭造型的2个影响因子为自变量,以透平总总效率为因变量,设计了25组正交试验,各因子水平的取值如表6所示。正交优化后所得最佳总静效率和总总效率分别提升了0.25百分点和0.57百分点,扭静叶匹配优化后的扭动叶的总总效率高于静叶单独扭转优化,对比结果如表7所示。表8为利用极差分析法得到的静叶扭转与动叶扭转各因子的最佳取值,此时静叶反扭且扭角沿展向减小,动叶正扭。

表6 扭造型影响因子水平取值

表7 扭静叶匹配扭动叶的正交优化结果

表8 静叶扭转与动叶扭转各因子的最佳取值
图10为扭造型静叶吸力面径向压力梯度分布图。如图10(b)所示,扭静叶顶部30%~70%弦长区域正负压力梯度掺混的面积变大且在尾缘处出现新的掺混区域,使得静叶出口尾缘处的流动变得更加不均匀。静叶中部压力梯度有所减小,随着向叶根方向发展,不同方向压力梯度掺混的强度呈现递增的趋势,流体流经叶片中下部时的能量损耗增大,流速降低,使得静叶出口该区域主流流速下降。如图10(c)所示,扭静叶顶部正负压力梯度掺混的面积比图10(a)所示原始静叶大,叶片中部存在较大的压力梯度减小的区域,减弱了通道内的二次流强度。在50%~80%叶高区域,图10(c)所示静叶沿尾缘方向的径向压力梯度均比图10(a)、图10(b)所示静叶小,这也削弱了静叶出口主流区流体与尾迹区流体相互干扰的强度。

(a) case 1静叶
图11为扭造型静叶出口熵增沿展向的分布图。如图11(b)所示,扭静叶出口熵增主要集中在尾迹区上部与下部,在中部区域沿展向的变化不大。叶片上部由于静叶尾缘区域存在不同方向的压力梯度掺混作用,其熵增比图11(a)所示原始静叶大;而在叶片下部,叶片前段不同方向压力梯度掺混的作用使得出口处主流速度下降,该区域熵增较原始静叶有所减小。如图11(c)所示,扭静叶出口熵增较原始静叶明显减小,10%~80%叶高的尾迹熵增削弱最为显著,紊乱程度下降。

(a) case 1静叶
图12为扭造型静叶所匹配的动叶通道内以及出口处的熵增沿展向的分布图。如图12(b)所示,扭静叶所匹配的初始动叶通道内以及出口处的熵增大于590 J/(kg·K)的面积较图12(a)所示动叶有所减小,而熵增大于520 J/(kg·K)的面积有所增大,说明由涡系结构引起的紊乱强度有所下降,但紊乱范围有所增加。如图12(c)所示,扭静叶所匹配的优化扭动叶顶部熵增相比图12(a)所示动叶变化不大,而在叶片下部熵增削弱较为明显,尤其在靠近叶根尾迹区,说明扭静叶匹配优化后的动叶流动情况有所好转。

(a) case 1动叶
图13为扭造型静叶、动叶出口总压损失系数沿展向的分布图。对于静叶出口,case 4和case 5的叶片总压损失系数均值分别为0.053 3和0.051 8,相较case 1分别减小6.49%和9.12%。如case 4所示扭静叶,叶片中部总压损失较为均匀,总体而言较原始静叶有所减小,但在叶片上部总压损失增大;case 5的扭静叶在10%~80%叶高处的总压损失较原始静叶有所减小,说明其流动情况有所改善。对于动叶出口,case 4和case 5的叶片总压损失系数均值分别为0.254和0.222,相较case 1分别增大7.63%和减小5.93%;case 4的动叶在10%~30%叶高处的总压损失系数变化较大,其峰值位置较原始动叶上移了约5%叶高,与上文动叶出口熵增分布所表现的情况一致;case 5的动叶下部总压损失比原始动叶小。

(a) 静叶总压损失系数
2.3 掠造型的应用
以静叶掠造型的1个影响因子和动叶扭造型的2个影响因子为自变量,以透平总总效率为因变量,设计了25组正交试验,各因子水平的取值如表9所示。正交优化后所得最佳总静效率和总总效率分别提升了0.19百分点和0.25百分点,掠静叶匹配优化后的扭动叶的总总效率高于静叶单独掠优化,对比结果如表10所示。表11为利用极差分析法得到的静叶掠与动叶扭转各因子的最佳取值,此时静叶后掠,动叶正扭且扭角沿展向增大。

表9 掠造型影响因子水平取值

表10 掠静叶匹配扭动叶的正交优化结果

表11 静叶掠与动叶扭转各因子的最佳取值
图14为掠造型静叶吸力面径向压力梯度分布图。如图14(b)所示,前掠静叶前段负方向压力梯度区域较图14(a)所示原始静叶明显增大,叶片中后段径向压力梯度有所减小,有利于减弱静叶出口流动紊乱程度;静叶顶部2个方向的压力梯度掺混面积有所增大,在静叶出口处存在较小的掺混区域。如图14(c)所示,后掠静叶中部前缘处存在较大的径向压力梯度为0 kg/(m2·s2)的区域,削弱了静叶进口处径向二次流强度;叶片中后段径向压力梯度较图14(a)所示静叶也有所减小;静叶顶部2个方向的压力梯度掺混面积相比图14(b)所示静叶变化不大。

(a) case 1静叶
图15为掠造型静叶出口熵增沿展向的分布图。如图15(b)所示,前掠静叶出口熵增主要集中在叶根尾迹区,沿展向尾迹区的熵增呈现减小的趋势,在30%~50%叶高处熵增较图15(a)所示原始静叶有所减小。如图15(c)所示,后掠静叶出口熵增主要集中在叶根尾迹区,熵增大于590 J/(kg·K)的面积比原始静叶、前掠静叶小;沿展向尾迹区的熵增呈现减小的趋势,在20%~50%叶高处熵增较原始静叶削弱明显;叶片上部尾缘处出现正负压力梯度掺混的区域,后掠静叶出口熵增略有增大。

(a) case 1静叶
图16为掠造型静叶所匹配的动叶通道内以及出口处的熵增沿展向的分布图。如图16(b)所示,前掠静叶所匹配的初始动叶上部通道内的熵增相比图16(a)所示动叶变化不大,出口处熵增大于580 J/(kg·K)的面积有所增大;叶片下部熵增大于580 J/(kg·K)的面积亦有所增大,而大于520 J/(kg·K)的面积有所减小,说明该动叶内紊乱强度有所上升,但紊乱范围有所减小。如图16(c)所示,后掠静叶所匹配的动叶顶部熵增较图16(b)所示动叶有所减小,而在叶片下部动叶出口处熵增削弱明显,说明后掠静叶所匹配的动叶下部二次流损失下降。

(a) case 1动叶
图17为掠造型静叶、动叶出口总压损失系数沿展向的分布图。对于静叶出口,case 6和case 7的叶片总压损失系数均值分别为0.055 2和0.054 9,相较case 1分别减小3.16%和3.68%;叶片中部总压损失较为均匀,在60%叶高以下小于原始静叶,而在60%叶高以上较原始静叶略有增大。对于动叶出口,case 6和case 7的叶片总压损失系数均值分别为0.248和0.233,相较case 1分别增大5.08%和减小1.27%;case 6的动叶总压损失系数沿展向均略有增大,而case 7的动叶总压损失系数在40%叶高以下较小。
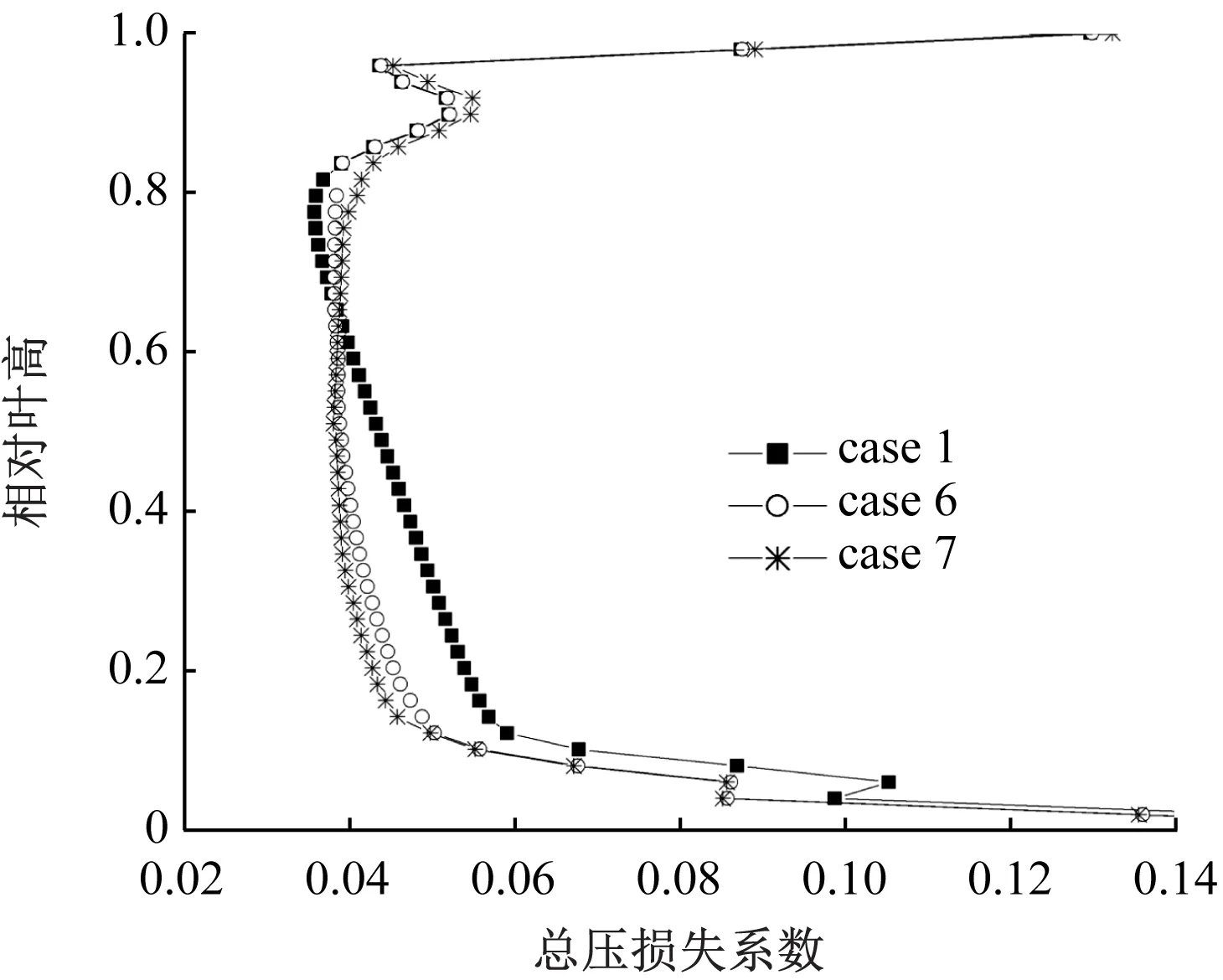
(a) 静叶总压损失系数
3 结 论
(1) 对静叶分别进行弯、扭、掠改型优化并匹配优化后的扭动叶,总静效率分别提升了0.22百分点、0.25百分点和0.19百分点,总总效率分别提升了0.29百分点、0.57百分点和0.25百分点;对于初始透平,静叶的单独改型优化会降低透平级效率。
(2) 对于弯造型,最佳匹配状态下的静叶正弯,动叶正扭且扭角沿展向增大。正弯静叶叶顶前缘径向正压力梯度增大,叶片中部压力梯度减小;静叶出口熵增集中在叶片上、下部,动叶下部熵增有所减小,静叶、动叶总压损失系数分别减小1.93%和2.12%。
(3) 对于扭造型,最佳匹配状态下的静叶反扭且扭角沿展向减小,动叶正扭。反扭静叶中后段径向压力梯度减小;静叶、动叶出口熵增均有所减小,静叶、动叶总压损失系数分别减小9.12%和5.93%。
(4) 对于掠造型,最佳匹配状态下的静叶后掠,动叶正扭且扭角沿展向增大。后掠静叶中部径向压力梯度较小;静叶出口中下部熵增有所减小,动叶出口下部熵增削弱明显,静叶、动叶总压损失系数分别减小3.68%和1.27%。
