基于嵌套饱和的四旋翼无人机吊挂负载控制器设计*
2023-10-18余志凯黄子豪傅瑾瑜蒋宪鑫
余志凯,黄子豪,傅瑾瑜,蒋宪鑫,辛 颖
(1. 中国人民解放军93145部队·上海·201109;2. 上海航天控制技术研究所·上海·201109)
0 引 言
四旋翼无人机因为其低廉的成本、丰富的扩展、灵活的机动能力,以及典型的欠驱动特性,一方面在工业检测、农业植保、商业娱乐、军事攻防等领域应用广泛,另一方面可作为各种算法以及传感器的理想验证平台[1]。四旋翼吊挂负载的研究既有切实的运输、消防、救援等实际应用,又有探索针对高耦合和强欠驱模型控制理论的价值。
Guerrero等提出了具有较好鲁棒性的互联和阻力分配的无源控制器,分别设计了依赖与不依赖于吊挂角度的控制律,实现了点到点机动下摆动的抑制[2-4]。范云生等人利用扩张状态观测器对扰动及不确定性等优秀的估计能力设计非线性控制器,并通过QBall2四旋翼无人机携带吊挂模型的三维螺旋轨迹进行仿真验证,有效实现了对吊挂摆动的快速抑制与轨迹的精确跟踪[5]。Lyu等人在四旋翼吊挂负载系统建模中考虑了吊挂风扰,设计了具有指数收敛稳定性的非线性级联控制器[6],之后又采用有限时间控制方法,进一步提高了系统的收敛速度与鲁棒性[7]。鲜斌课题组是国内对该系统研究较多的团队,其文章主要基于能量函数开展,利用自适应控制或神经网络等方法估计吊挂变化或外界扰动,各控制器的有效性都经过了理论与试验的双重验证[8-10]。梁晓等人提出一种简单判别系统微分平坦的方法,并以此为基础通过动态反馈线性化实现轨迹跟踪控制[11]。焦海林等人则分析了吊挂系统本身的摆动特性,借用抑制移动容器内液体晃动的加速度补偿技术,有效减少了机体移动引起的副作用实现负载摆动的抑制[12]。Omar等人根据吊挂单摆的周期,设计相关延时反馈的抑摆控制器,只需修饰设计轨迹即可实现摆角抑制,便于直接移植应用于已有成熟算法平台(例如PX4固件),并利用Gazebo搭建了硬件在回路仿真平台[13-14],之后针对延时又进一步设计了模糊控制器,增强了抑摆的有效性[15]。
上述方法主要解决了四旋翼无人机吊挂负载控制在两个方面的问题:1)四旋翼机体抗吊挂干扰的稳定控制;2)吊挂摆角的最终稳定收敛。但是四旋翼无人机在大幅度位置机动过程中吊挂摆角的抑制不够突出,机动过程中的最大摆角容易随着机动的增大而明显增大。受文献[16]的启发,可以通过合理设置饱和区间从而抑制摆角,但因文献[16]的控制效果不够明显,饱和控制方法有进一步提升空间。
本文通过一种嵌套饱和控制方法,设置虚拟输入饱和来限制实际最大过载,有效限制机动加速度,从而减小摆动。并考虑到嵌套饱和在抑制干扰方面没有明显优势,所以针对吊挂变化影响不敏感的垂直位置,设计基于扩张状态观测器的控制器,通过结合不同算法的优势得到本文所提控制器。
1 四旋翼吊挂系统建模
四旋翼无人机本身为四输入六自由度的典型欠驱动系统,携带吊挂负载后(假设飞行中吊绳始终处于拉伸状态)额外增加两个自由度,使得系统的欠驱动特性更加显著,系统复杂度进一步增加,其三维示意图如图1所示。

图1 四旋翼吊挂系统三维示意图Fig.1 Three-dimensional schematic diagram of quadrotor suspended payload system
图1中的四旋翼机体为X形,在四旋翼中心建立固连的机体坐标系obxbybzb,并以地面起飞位置为原点建立惯性坐标系oixiyizi,φ,ϑ,ψ为四旋翼机体分别绕xb,yb,zb轴旋转的姿态角,并定义惯性系到机体系的欧拉角旋转顺序为z(ψ)→y(ϑ)→x(φ)。吊挂摆角α,β为吊绳在平面obybzb上的投影,分别与obzb轴、吊绳的夹角。定义单机质量为M,吊挂质量为m,吊挂绳长为l,惯性系下旋翼升力在各轴的分力为Fx,Fy,Fz,机体系下沿各轴的力矩为τx,τy,τz,转动惯量为Jxx,Jyy,Jzz。
(1)

(2)
通过计算可得8个方程构成的方程组作为三维数学模型,由于结果较为繁琐冗长,且仅在仿真中使用,下文控制器设计中没有全部使用,这里不再给出具体形式。
考虑四旋翼无人机小角度飞行时,吊挂系统水平运动在正交方向耦合较小,为了便于控制器设计,此处给出oiyizi二维平面的简化形式
(3)
2 控制器设计
若控制器设计合理,则能保证摆角始终处于小角度状态,结合式(3)的第三条方程可知,此时摆角的余弦值接近1而正弦值接近0,易得摆角变化主要取决于y向变化,与z向相关性较小。因此,本文通过y向控制同时实现摆角控制,z向独立控制,其变化视为对摆角的小幅度扰动,反之亦然,分别设计水平、垂直位置控制器。
2.1 垂直位置控制器
考虑到四旋翼垂直位置与摆角相互耦合,垂直位置控制器又不直接作用于摆角控制,为了提高z向抗扰能力,引入自抗扰控制中的扩张状态观测器估计z向总扰动,抑制后续的干扰,以提升控制性能。
为了适应三维情况,利用式(2)计算zi轴结果,并定义zi轴的总扰动为Δdz,经整理得到如下表达式
(4)
其中
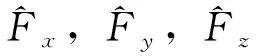

(5)

(6)
式中,κ1,κ2,κ3,a1,a2,a3,δ为观测器参数,sign(·)为符号函数。
在得到扰动估计的前提下,得到z轴垂直位置控制器
(7)
式中,zc为期望位置指令,Kp,Kd为非负的控制参数。
2.2 摆角抑制控制器
四旋翼吊挂系统作为高度欠驱动系统,在z轴方向独立控制前提下,本文所设计的控制器通过摆角抑制控制力uα与水平y轴的控制力Fy叠加的方式实现摆角α与y轴的完全耦合。
四旋翼机体在空中稳定飞行(匀速直线或悬停状态)时,吊挂在水平位置的摆动可简化为吊绳上端的水平移动与吊挂负载单摆运动的叠加,从而得到如下摆角控制器
(8)
其中kα为大于零的控制参数。
下面进行稳定性证明。构造如下李雅普诺夫函数
(9)

使用“do/does/did+v.”构式既能表达变化,也能表达移动。变化是抽象的移动,移动是具体的变化。造成变化和移动的可以是物理力,也可以是心理力,甚至是社会力。例7中,他们受到心理感受的无形的力而改变态度,例8是物理力的作用,是施事者就具体物体发出的力量,例9则是来自社会的约束力。使用目标构式表达变化或移动,起到凸显力作用的效果。
(10)
将式(8)的控制器代入上式,易得
(11)
摆角理论上渐近收敛。
2.3 水平位置控制器
水平位置控制器主体采用嵌套饱和控制器,存在如下引理[17-18]:
对于如下形式的n阶多次积分系统
(12)
其中umax为正数,表示执行器的最大输出大小,令
(13)
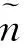
(14)
原状态空间经过形式如p=Tx的状态方程变换为Teel标准型
(15)
其中
等价变化矩阵为
(16)
当n为偶数有
(17)
当n为奇数有
(18)
已知ε为正数,定义饱和函数σε
(19)
若给定如下控制律,能使系统镇定
(20)
其中

根据上述引理进行控制器设计,对模型进行小角度线性化,并将四旋翼无人机视为无吊挂的系统进行推导设计。考虑到嵌套饱和控制器无法直接控制水平分力,而需姿态角变化实现水平位置控制。所以本文将抑摆控制器的输出转化为姿态角零位补偿,从而引入到嵌套饱和控制器中,得到如下模型
(21)
其中φε=φ-φb,φb=-uα/(Mg)为角度零位补偿,用于近似水平分力抑制吊挂摆动。
对模型进行简单整理,易得状态空间表达式
(22)
(23)
利用式(16)可反推变换矩阵,易得变换后的系统状态变量
(24)
得到水平位置控制器
(25)
3 仿真验证及分析
为了验证本文设计控制器的控制效果,尽可能接近实物试验便于后续飞行验证,本文基于已有四旋翼无人机吊挂系统实物的模型参数,考虑了传感器、电机等多种影响因素,采用连续模型和离散控制器进行三通道仿真,计算多组典型工况并加以分析。
四旋翼吊挂模型的主要参数:M=1.5kg,m=0.1kg,l=1.0m,Jxx=0.022kg·m2。本文控制器主要参数:κ1=100,κ2=300,κ3=1000,a1=1,a2=0.5,a3=0.25,δ=0.02,Kp=2,Kd=2.8,kα=2,ε1=0.11,ε2=0.266。
首先为了验证抑摆控制器的效果,对比了嵌套饱和控制有无引入抑摆角度零位补偿两种情况,在z轴方向上,0s时输入幅值为8m的阶跃信号,在y轴方向上,10s时输入幅值为8m的阶跃信号,仿真结果如图2所示。引入扩张状态观测器的z轴方向位置响应抗扰能力较强,几乎不受抑摆控制器补偿的影响;y轴方向位置响应在姿态角有无抑摆补偿情况下总体变化趋势差别不大,但有抑摆补偿时超调有少许增加;抑摆补偿下姿态角变化有些许增大,用以补偿摆动;引入抑摆补偿后,吊挂摆角的全过程变化趋于平稳,当位置到达目标点附近后,摆角会快速收敛并趋近于零,不再有明显振荡。
目前已有的四旋翼吊挂系统控制器几乎都能保证位置机动到位后的摆角快速收敛,本文通过引入控制效果较好的自适应控制器进行对比,自适应控制器设计可见文献[10],但不包括姿态控制,仿真时使用串级PID进行姿态控制。利用同一组控制参数,分别进行了z轴和y轴方向上,输入信号为幅值2m的阶跃信号的小范围位置机动工况仿真,结果如图3所示,以及z轴和y轴方向上,输入信号为幅值6m的阶跃信号的大范围机动工况仿真,结果如图4所示。

图3 小范围位置机动控制器效果对比Fig.3 Effect comparison of small range position maneuvering controllers

图4 大范围位置机动控制器效果对比Fig.4 Effect comparison of large range position maneuvering controllers
首先从z轴控制器进行对比,两种工况下本文所提控制器与自适应控制器均无产生超调,但本文控制响应明显收敛更快,在幅值较大的阶跃指令作用下尤为明显。不同工况下,两种控制器在y轴方向上的位置响应快慢各有优势,但本文控制器作用下响应的上升时间、调节时间以及超调量等指标波动幅度更小,响应趋势较为一致;而自适应控制器的参数在小范围位置机动工况下控制性能较好,但在阶跃指令变化较大后响应曲线变化明显,超调量及调节时间显著增大。y轴方向的控制间接作用于姿态控制,在幅值较大的阶跃输入信号作用下自适应控制器更容易产生过大的姿态指令以提高速度,从而更容易产生姿态角的饱和;本文所采用的嵌套饱和控制方法,对位置、姿态分级产生饱和控制效果,姿态角反而不易饱和。
自适应控制器的最大摆角在图3中约为2.3°,图4中约为9.0°,明显随指令信号的增大而增大。本文所提控制器的最大摆角在图3中约为2.8°,图4中约为3.8°,摆角抑制效果受指令信号影响较小。显然在幅值较小的阶跃信号作用下自适应控制抑制效果略优,但本文所提控制器更能显现出对最大摆角的抑制,实际应用更有优势。
对本文所提控制器进行y轴方向上不同阶跃输入信号情况下的仿真,结果如图5所示。y轴方向上的控制响应速度近似且较快,超调量始终保持在10%以内。y轴在1m,3m,6m,10m阶跃信号下对应的最大摆角大小分别约为1.7°,2.8°,3.8°,3.6°,即使在水平方向上做大范围机动,摆角大小都控制在4°之内。除单位阶跃信号外,其余信号响应下摆角与姿态角变化趋势近似,两者角度响应在纵轴正负半轴的占比接近。体现了嵌套饱和控制器通过较为稳定均衡地分配位置机动的加减速阶段,减小加速度凸变引起吊挂剧烈摆动的特点。

图5 多范围位置机动控制器响应对比Fig.5 Response comparison of multi-range position maneuvering controllers
4 结 论
本文研究了四旋翼无人机吊挂负载控制系统,针对多数控制方法忽略的大机动过程中吊挂最大摆角抑制问题,提出了一种综合控制方法,其借助扩张状态观测器独立控制z轴方向运动,以抑制吊挂干扰,减小耦合。该方法采用嵌套饱和控制方法抑制加速度剧烈变化,以及通过抑摆控制器以姿态角零位补偿的形式引入水平控制器。通过与自适应控制器进行仿真对比,验证了机动过程抑摆的有效性以及多工况适应性。但本文未考虑未知吊挂质量与绳长的情况,后续将探索饱和控制与自适应控制相结合的方法。
