拦截机动目标的三维协同中末一体化制导律*

陈宏旭，于江龙，陈 扬，董希旺，3，李清东，任 章

(1. 北京航空航天大学 自动化科学与电气工程学院·北京·100191；2. 上海航天控制技术研究所·上海·201109；3. 北京航空航天大学 人工智能研究院·北京·100191)

0 引 言

近年来，随着来袭目标的速度不断增大，机动性不断增强，作战样式逐渐多样化，对这类空中威胁目标的拦截造成极大挑战。传统的拦截方案是单枚导弹拦截目标，但由于目标机动性不断增强，“一对一”的拦截成功率不断降低，因此，采用协同制导的方式，多枚导弹拦截一个机动目标成为当前的研究热点[1-4]。

目前，国内外学者在协同制导领域已经提出了很多解决方案。文献[5]提出了一种二回路(决策回路和控制回路)的时间协同制导律，根据剩余飞行时间设计期望的一致量，设计反馈控制器，实现打击时间的一致性。文献[6]提出了领导者-跟随者模式的时间协同制导律，选取一枚导弹作为领弹，为领弹设计相应的导引方法，为其余导弹设计跟踪控制器跟踪领弹，实现时间协同。文献[7]根据变结构控制理论，设计了有限时间收敛的带有攻击角约束的制导律。文献[8]基于模型预测，采用优化方法实现了带有攻击角约束的制导律。文献[9]设计了带有角度约束的协同制导律，多弹采用一定的编队队形增大拦截域，有效拦截大机动目标。文献[10-11]基于改进比例导引法以攻击角度约束作为偏置项，进而设计了时间角度协同制导律。针对拦截问题，文献[12]提出了以动能拦截器为对象的拦截末制导律。文献[13]提出了二维场景下基于覆盖策略的多枚弱机动能力拦截弹协同拦截大机动目标的协同制导律。文献[14]研究了三维场景下导弹逆轨拦击机动目标的最优制导律。文献[4]提出了一种新型的协同末制导架构，并且在末制导段实现了对目标的有效拦截。文献[15]研究了多领导者-跟随者模式下的多飞行器协同拦截机动目标的分布式协同围捕制导问题。文献[16]研究了多对多的协同博弈制导问题。

综上所述，现有的多数拦截机动目标的制导律是在二维场景下，只考虑末制导，随着来袭目标的机动能力提升和机动策略变化，较难满足作战精度要求。因此，研究三维场景下，结合中末制导的协同拦截制导律具有重要意义。

本文针对上述问题，基于二回路的协同制导架构，提出拦截机动目标的三维协同中末制导律。首先，针对末端目标机动能力较大的情况，使得我方拦截弹的可达区域之和完全覆盖目标的机动逃逸区域，同时解算出中末交班的阵位约束。其次，为了保证末制导良好的交班阵位，研究基于预测命中点的协同中制导律，降低中段导弹过载，保证中末交班。最后，设计三维仿真实验，验证协同中末制导律的有效性。

1 三维协同制导建模

在导弹和目标的运动空间内，其多弹协同三维非线性运动模型如图1所示。其中Mi代表第i枚导弹，T代表目标；VM和VT分别为导弹速度和目标速度，假设每枚导弹的速度大小都是一样的，即均为同构导弹；ri为导弹与目标之间的距离；θM，i和φM，i分别为导弹的弹道偏角和弹道倾角；θT和φT分别为目标的弹道偏角及弹道倾角。

图1 多弹协同三维非线性运动模型Fig.1 Multi-projectile cooperative three-dimensional nonlinear motion model

假设导弹和目标的速度方向都近似在导弹和目标的连线附近。那么，在纵向平面上的弹目相对运动方程可以写为

(1)

其中，aM，lon，i为导弹i的纵向加速度，aT，lon，i为目标相对于导弹i的纵向加速度；ηM，i和ηT，i分别为导弹i和目标在纵向平面上的速度前置角；VM，lon，i和VT，lon，i分别为导弹i和目标在纵向平面上的速度分量，即

(2)

其中，σM，i和σT，i分别为导弹i和目标在侧向平面的速度前置角。

同理，在侧向平面上的弹目相对运动方程可以表示为

(3)

其中，aM，lat，i为导弹i的侧向加速度，aT，lat，i为目标相对于导弹i的侧向加速度；VM，lat，i和VT，lat，i分别为导弹i和目标在侧向平面上的速度分量，rlat，i为导弹i与目标之间的距离在侧向平面上的投影，即

(4)

2 末制导协同制导律设计

2.1 末制导协同打击策略

在多导弹协同打击目标的过程中，在导弹自身存在过载约束的情况下，每枚导弹都存在一个可攻击区域，记为AF。此外，对于机动目标来说也存在一个最大逃逸区域，这里定义为当目标以不同的加速度方向，始终按照最大加速度大小飞行时可到达的区域，可记为AE。将三维的目标最大逃逸区域及导弹可攻击区域用上一节所定义的侧向加速度与纵向加速度在二维坐标系下表示，如图2所示。

图2 覆盖策略描述示意图Fig.2 Overlay policy description diagram

(a)π/arcsinμ为整数

(b)π/arcsinμ为小数图3 情况1下的协同覆盖策略示意图Fig.3 Cooperative coverage diagram in case 1

若π/arcsinμ为小数，则覆盖不均匀，那么所需小圆数量应为向上取整后的结果，即n=[π/arcsinμ]，如图3(b)所示。

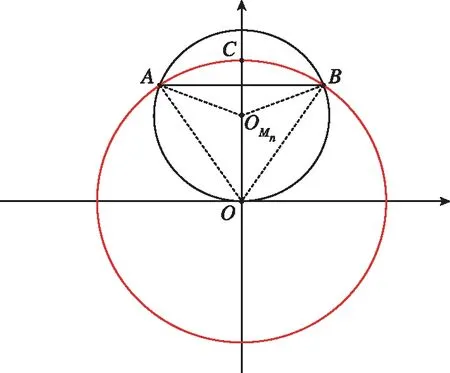
图4 情况2下的协同覆盖示意图Fig.4 Cooperative coverage diagram in case 2

单个小圆所覆盖的大圆弧长为

(5)

情况 3：当小圆半径为0.5时，用情况 1 和情况 2 中的方法都不能实现对大圆的完全覆盖，此时需要在大圆圆心处增加一个小圆，然后让其余小圆覆盖大圆圆周以及中心小圆圆周，如图5所示。

图5 情况3下的协同覆盖策略示意图Fig.5 Cooperative coverage diagram in case 3

因为大圆中心必有一个小圆，在外圈的小圆除了要覆盖大圆圆周外，还应该保证内圈小圆的圆周被完全覆盖，才能保证整个大圆被完全覆盖。由几何关系可得

(6)

此时，

∠DOMnF=π-

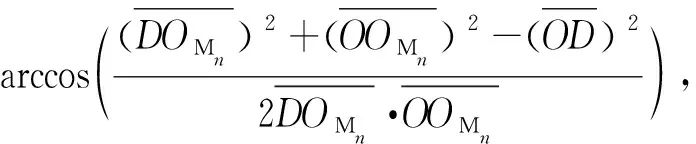
(7)

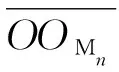
(8)

则外圈小圆的圆心位置为

(9)

2.2 协同末制导律设计

三维协同制导律在三维协同制导模型的基础上，为了满足上述标准弹道的特点，分别设计了第i枚导弹在纵向平面上的纵向加速度aM，lon，i和侧向平面上的侧向加速度aM，lat，i。其制导律的形式如下所示

(10)

其中，N为比例导引律中的导航比，Blat，i和Blon，i分别为导弹在侧向平面和纵向平面上的协同偏置项。

将上式中的aM，lon，i和aM，lat，i代入式(1)和式(3)可得

(11)

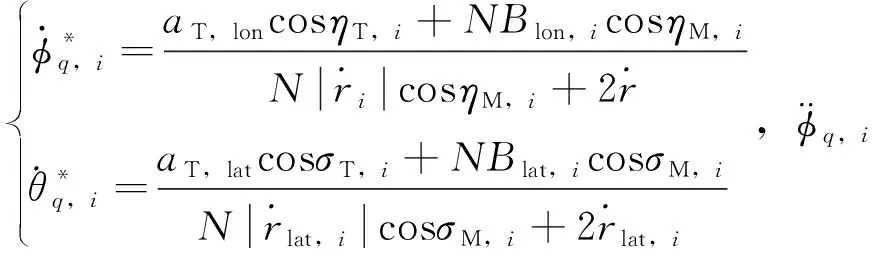
在命中点处(t=tf)，ri，tf=0，从而ri，lat，tf=0，因此式在命中点处时，两个等式的左边为零，这就要求等式右边也为零，即

(12)

通过最小化初始时刻和命中点的过载，从而降低整个打击过程中的过载。即

(13)

式中0表示初始时刻t=t0，f表示命中时刻t=tf。当导弹i以标准弹道拦截过载为aT，i，s的机动目标时，同样根据三维建模可将目标过载aT，i，s分解到水平面上的过载aT，i，s，lat和垂直平面上的过载aT，i，s，lon，再结合式(10)～(13)可得制导律中的偏置项为

(14)

导弹i在初始时刻应满足

{(VT,lon,i,0cosηT,i,0-VM,lon,i,0cosηM,i,0)(VM,lon,i,0sinηM,i,0-VT,lon,i,0sinηT,i,0)+Blon,iri,0=0
(VT,lat,i,0cosσT,i,0-VM,lat,i,0cosσM,i,0)(VM,lat,i,0sinσM,i,0-VT,lat,i,0sinσT,i,0)+Blat,irlat,i,0=0

(15)

导弹在命中点处应满足

(16)

导弹i的剩余飞行时间可近似为

(17)

再对式(1)的第一个方程求导，并结合式(1)第五个方程可得

(18)

对式(3)的第一个方程求导，并结合式(3)第六个方程可得

(19)

结合式(10)和式(18)得

(20)

(21)

对上式进行积分，可得

(22)

同理，水平面上初始时刻和命中时刻的前置角关系可表示为

(23)

综上，根据导弹和目标在初始时刻和命中点的前置角关系以及制导律设计项，整理为方程组

(24)

3 中制导协同制导律设计

3.1 预测命中点求解

预测命中点的求解[17]可以采用以下步骤进行。

步骤一：确定初始制导弹与目标的初始位置(xm，ym，zm)，(xt0，yt0，zt0)，经过Δt时间后，目标的位置变为(xt1，yt1，zt1)，假设该点即预测命中点，预测命中点的显式求解

(25)

步骤二：将上一步骤中求得的(xt1，yt1，zt1)作为拦截弹的目标点，采取经典的比例导引律飞向目标，可以大致估计拦截弹需要的剩余飞行时间tgo，则拦截弹的飞行时间为tm=t0+tgo，目标的飞行时间tt=t0+Δt。

步骤三：令ΔT=tt-tm，若|ΔT0|<Δt(Δt为所取的时间步长)，则(xt1，yt1，zt1)就可以认为是预测命中点；若|ΔT0|>Δt，则重复步骤一和步骤二的内容，计算下一时刻点tt+1=tt+Δt时刻目标的位置(xt2，yt2，zt2)，并将该点看作预测命中点。重复计算拦截弹导引至这一时刻虚拟目标点所需要的剩余飞行时间tgo。

步骤四：继续判断目标与拦截弹的飞行时间差ΔT的绝对值是否大于时间步长Δt，若大于，则重复上述步骤。直到上述关系式变成小于就得到了预测命中点。

3.2 协同中制导律设计

基于预测命中点的修正比例导引律可设计为

(26)

其中，θ为拦截弹航向角，qp为期望的视线角，v为导弹速度。

预测命中点比例导引修正项的具体形式

Δac=k1(θ-qp)

(27)

时间协同偏置项[18]可以表示为

aξ,i=Kiriξi

(28)

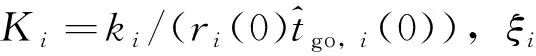
其中，

带有攻击角限制的末制导律[19]设计如下

(29)

其中，αi=θi-Nqi+(N-1)θd，i，θd，i为导弹i期望的角度约束，N≥3，Kζ，i≥1。

综上，基于预测命中点设计和中末交班阵位设计时间角度协同中制导律

(30)

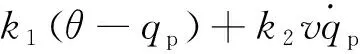
4 仿真结果及结果分析

4.1 仿真结果

以多弹齐射的作战方式为例来对上述的研究成果进行数字仿真与验证，采用4枚拦截弹拦截，导弹最大过载38g(g为重力加速度)，目标最大过载15g，末制导开机距离为15km，导航比为3。目标在4～5s纵向以最大过载15g机动，5～6s侧向以过载15g机动，10～11s纵向以过载15g机动。4枚导弹的覆盖策略示意图如图6所示，*为解算出的导弹在末制导初始时刻的阵位。

图6 覆盖策略示意图Fig.6 Cooperative coverage diagram

中末制导弹道如图7所示。

(a)中末制导弹道图

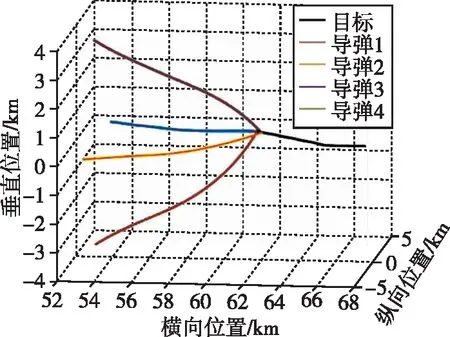
(b)末制导弹道图图7 中末制导弹道图Fig.7 Mid-terminal guidance trajectory diagram

纵向、侧向平面角度误差如图8所示。

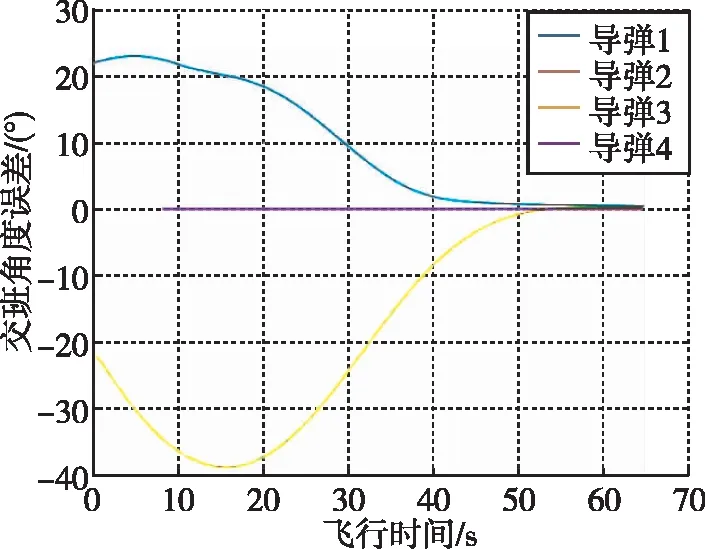
(a)纵向平面误差图

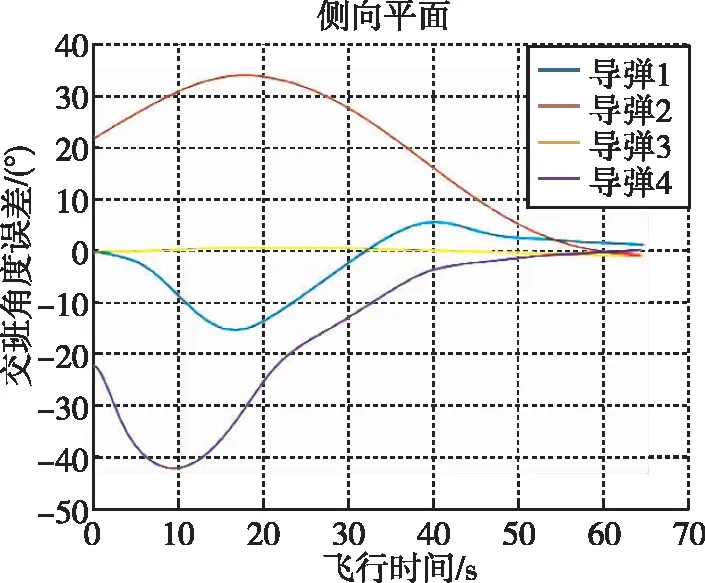
(b)侧向平面误差图图8 纵向侧向平面角度误差图Fig.8 Longitudinal - lateral plane angle error diagram

导弹过载如图9所示。

图9 导弹过载图Fig.9 Missile overload diagram

4.2 结果分析

由图6～图9所示，基于圆域覆盖算法的协同末制导实现了对目标逃逸域的有效覆盖，协同中制导在中制导段实现了时间和角度协同，同时，导弹的中末制导需要过载均小于目标机动过载，小于导弹可用过载。在中制导结束时，导弹以设计的交班角度到达，平均角度误差为0.8606°，时间一致性误差为0.1291s，交班位置误差为2.69%，在末制导阶段，协同打击策略分配了4枚拦截弹的拦截阵位，导弹的最小脱靶量为0.3693，在命中点附近最大过载为9.32g，小于机动目标的最大过载15g，通过协同中末制导实现了有效拦截。

5 结 论

本文研究了拦截空中大机动目标的协同中末一体化制导问题。在所提出的基于圆域覆盖算法的协同打击策略的基础上定义了导弹的标准弹道，即代表导弹的小圆圆心所在的位置即为该阵位下导弹按标准弹道飞行时目标的机动大小。然后给出了基于改进比例导引律的协同制导律形式，推导了在满足该协同打击策略下的末制导初始阵位要求，以及该协同制导律各导弹所需要的偏置量大小。根据末制导对交班阵位的要求，为了实现精准中末交接班，采用预测命中点的方法，将导弹导引向交班阵位，设计时间角度协同中制导律，最终实现有效拦截。但是本文未考虑目标在中制导段的机动情况，因此后续将研究中制导段目标机动后基于预测命中点修正的制导律设计问题。