基于数据驱动的弹性高超声速飞行器控制方法*

何飞毅，张莫楠，倪 昊，辛 颖，黄子豪

(1. 上海航天控制技术研究所·上海·201109；2. 陆装驻上海地区第三军事代表室·上海 ·201109)

0 引 言

高超声速飞行器采用基于乘波特性设计的升力体外形，在高超声速条件下具有高升阻比、高操纵性的特点，展现出了极强的长航时跨域飞行、高速机动轨迹变更等优点，得到了各国的广泛研究。高超声速飞行器在飞行过程中，飞行包线跨域大，其气动存在非线性强、不确定性大、耦合特征明显等特点，特别是在大动压飞行工况下表现出极强的静不稳定性，容易造成参数较大摄动情况下的控制品质下降。另一方面，由于采用最优升阻比设计和轻质结构外形，飞行器一阶、二阶固有振动频率低，发动机、制导飞控舱设备等弹上设备振动影响显著，随着飞行动压增大，飞行器振动模态与刚体控制耦合明显，进一步降低控制系统稳定裕度，严重时甚至使飞行器失稳。因此，如何在飞行器特性具有较大摄动时，高效实现大动压、大静不稳定下的刚体控制和弹性体抑制，对提高超声速飞行器飞行控制品质具有重要意义。

传统飞行控制系统设计一般基于精确的被控对象模型，通过离线设计的控制参数确保实际飞行过程中具有一定的稳定性和响应性能，例如LQR控制[1]、鲁棒控制[2]、反步法控制[3]、滑模控制[4]等，上述方法在面对高超声速飞行器严酷的飞行环境时，往往难以适应飞行器复杂多变的强不确定性影响。因此，需要研究一种能够根据飞行器输入输出响应信息，在线优化飞行控制性能的方法。针对上述问题，研究人员提出了一种融合动态规划(Dynamic Programming，DP)、强化学习(Reinforcement Learning，RL)和函数近似的自适应动态规划(Adaptive Dynamic Programming，ADP)方法[5]。该方法利用在线获取的输入输出数据，采用近似函数估计来构造系统性能指标评价函数，然后依据贝尔曼动态规划理论获得近似最优的控制策略，其作为一种基于数据学习和优化的智能控制方法，在解决具有未知特性的复杂系统最优控制问题中具有极大潜力，目前已经得到国内外学者的广泛研究[6]。

D Vrabie等提出了一种基于强化学习(Reinforcement Learning，RL)的连续系统控制的在线策略迭代方法，该方法不需要知道系统的动力学模型，仅仅通过对评价网络和执行网络的顺序更新，实现了系统的在线优化[7-8]。在此基础上，K Vamvoudakis等提出了评价网络和执行网络的同步更新策略，进而提高了控制性能在线优化的效率[9]。H Modares等为了进一步提高基于RL的自适应动态规划对执行机构饱和的适应能力，并解决在线优化过程中持续激励条件(Persistence of Excitation，PE)难以判别的问题，提出了一种基于积分强化学习和经验回放机制的自适应动态规划方法，不仅采用了当前的输入输出信息，还充分利用了历史数据优化控制系统性能，并且在稳定系统上进行了验证[10]。上述方法通过采集系统当前和过去的控制信号、状态反馈信号等信息，通过求解评价网络和执行网络权函数的梯度实时更新控制权重，但是优化过程中对系统稳定的要求过于严格，一旦更新的权重使系统发散，特别是对于静不稳定系统，往往难以获得收敛且可靠的结果。Jiang Y等针对不确定连续系统提出了一种鲁棒ADP控制方法(Robust Adaptive Dynamic Programming，RADP)，该方法基于最优性原理利用当前和过去信息，将控制权重更新问题转化为二次规划问题求解，使每一次控制更新都能得到使系统稳定的解[11]。

在上述研究的基础上，国内外学者也针对高超声速飞行器对象，开展了自适应动态规划方法的应用研究。郭建国等针对高超声速飞行器的速度和高度自适应控制问题，结合反步法与积分强化学习(Integral Reinforcement Learning，IRL)方法设计了最优反馈学习控制律，并通过Lyapunov稳定性理论严格证明了跟踪误差的一致最终有界[12]。汪雨劼等针对临近控制飞行器最优控制问题，将飞行器系统转化为标称跟踪系统和误差跟踪系统，基于RADP方法对误差跟踪系统设计了姿态控制律，实现了气动参数摄动情况下的近似最优跟踪控制[13]。李旭针对天地往返飞行器再入段姿态控制问题，基于滑模控制和ADP方法设计了内外双环控制器，并在外环引入ADP控制结构作为辅助控制[14]。

上述方法在一定程度上能够解决高超声速飞行器强不确定因素影响下的控制性能在线优化问题，但是，由于高超声速飞行器过载跟踪过程中获取的状态信息混杂了无法测量的振动和噪声干扰，将影响在线数据的利用效率，难以得到满意的控制参数优化结果。本文针对上述问题，首先对高超声速飞行器刚体、弹性体耦合模型进行了分析和建模，然后基于RADP方法设计了过载跟踪控制策略，在此基础上，通过RADP和陷波滤波方法的结合，形成适用于弹性高超声速飞行器的数据驱动自学习控制方法，最后通过仿真验证方法的有效性。

1 高超声速飞行器模型

1.1 刚体模型

飞行器纵向动力学模型如下

(1)

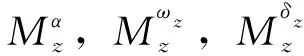
对上述纵向动力学模型进行小扰动线性化，可以得到如下控制模型

(2)

式中，a1～a5为动力系数。

1.2 弹性体模型

飞行器弹性振动模型可通过简化的一维梁模型表示，弹性振动简化动力学模型为

(3)

式中，qi为第i阶振动广义坐标，ζi为振动阻尼，ωi为振动频率，D1i，D2i，D3i为对应状态量的弹性振动动力系数。

由于传感器安装位置、线角耦合等因素影响，弹体振动会通过传感器耦合到控制器中，进而产生高频附加干扰信号，弹性振动对传感器输出的影响为

(4)

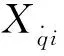
2 弹性高超声速飞行器数据驱动自学习过载跟踪控制方法

2.1 基本控制结构

结合高超声速飞行器刚体和弹性体模型，且只考虑1阶弹性振动，可以得到面向控制的小扰动线性化模型如下

(5)

式中

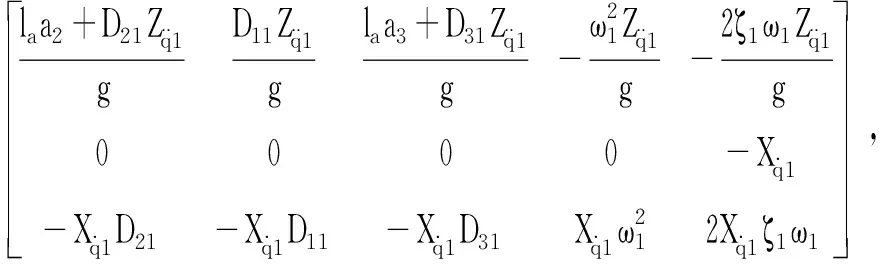
u=Gf(s)uc=Gf(s)KY

(6)

能够控制系统跟踪给定的期望指令。本文设计的目标则是在上述基本控制结构的基础上，基于控制量和状态量历史数据，在不确定参数影响下在线优化控制增益K，并尽可能降低弹性振动带来的影响。本文控制方案如图1所示。

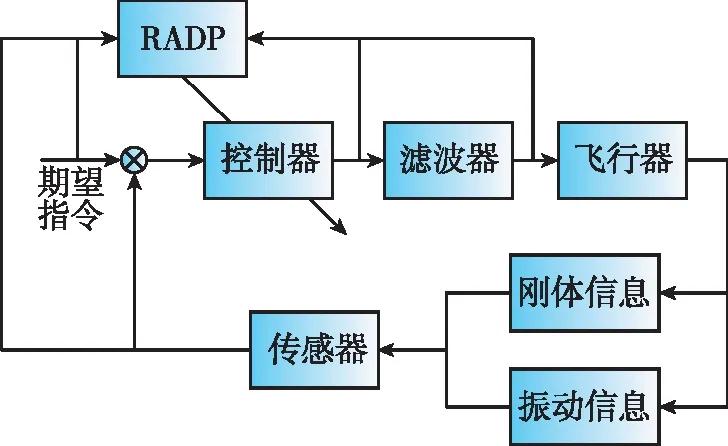
图1 控制方案Fig.1 Control scheme

2.2 基于RADP的过载跟踪控制

由文献[15]可知，RADP主要考虑状态反馈形式，当无弹性振动影响时，由于式(5)中矩阵C满秩，因此可将其变为如下状态空间模型

(7)

式中，A1=CAC-1，B1=CB。

通过在线求解最小化的二次型性能指标

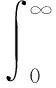
(8)

进而实现反馈控制律u=KY的在线更新。

由于系统状态矩阵A1和控制矩阵B1未知，因此无法采用传统解Riccati方程的方法求解控制增益K。为了实现在线学习，将控制量变为如下形式

u=KY+e

(9)

式中，e为一个较小的探测信号，保证在线学习过程中系统满足持续激励条件进而有可行解。

此时，在初始控制u0作用下，系统变为如下形式

(10)

令每一次迭代过程中ui=u0+e-vi，则系统可写为

(11)

考虑如下二次型Lyapunov函数

Vi=YTPY

(12)

当满足下式时

(13)

有

(14)

且要求每个样本区间[t，t+δt]内，均满足式(13)，则可得到如下Pi、ui+1的更新策略

YT(t+δt)PiY(t+δt)-YT(t)PiY(t)-

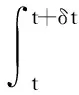
(15)

进一步得到

(16)

(17)

式中

因此通过最小二乘法求解式(17)，可以实现Pi、Ki+1的在线更新。

考虑跟踪过载指令Nyc，即令

uc=KY-KrNyc

(18)

使过载输出误差ΔNy=Ny-Nyc≈0。

根据闭环传递函数显然可以得到

(19)

则式(11)变为

(20)

此时定义

(21)

即

(22)

即可实现满足过载跟踪需求下的Pi、ui+1在线更新。

2.3 基于陷波滤波器的RADP控制方法

当系统中存在如式(5)所示的振动影响时，由于实际飞行过程中振动状态Q无法准确测量，且附加矩阵Cq存在较大的不确定性，将导致反馈控制律中存在难以区分的高频振动干扰，如下所示

(23)

式中，Y=CX。使得式(21)中的u0、ui不再是纯粹的刚体信号，而是包含了弹性振动干扰，且无法按照式(22)的方式转化为探测噪声，导致式(16)中等号左右两边均出现扰动，当弹性振动量级过大时，将直接影响Pi，Ki+1的求解精度，甚至得到错误的解。

因此本节通过结合陷波滤波器，在抑制弹性振动对稳定性影响的同时，提高振动影响下的控制参数在线更新效果。

为了便于分析，仅考虑1阶弹性振动作用，采用的陷波滤波器形式如下

(24)

式中，ξ1，ξ2，w1，w2为对应的设计参数，通过合理的设计，可以在特定频率对弹性振动实现一定幅值的衰减。

将其转化为状态空间形式有

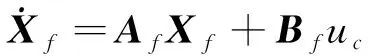
(25)

(26)

将其转化为式(7)所示的状态空间形式有

(27)

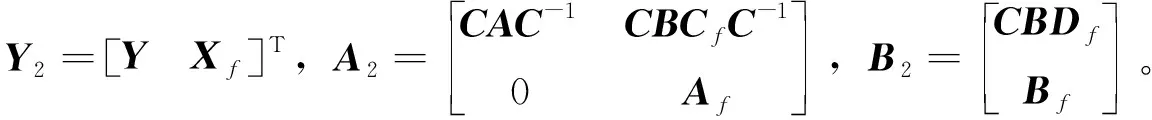
进一步将式(27)按照式(17)策略求解，即可在振动影响下准确求解Pi，Ki+1。

3 仿真验证

下面通过对比仿真验证本文弹性高超声速飞行器数据驱动自学习过载跟踪控制方法的有效性。

式(5)中对象模型参数如下所示

Cq=

在仿真中，设计初始控制参数为K=[1.0，1.0，0.19]，Q=diag[4，0，0]，R=1。设计陷波滤波器参数为

探测信号e设置为

e=0.2sin(6t)+0.2sin(12t)+0.2sin(18t)

(28)

下面分别对采用初始控制参数、无弹性振动RADP方法、不加滤波器RADP方法、本文加滤波器后RADP方法进行仿真，控制参数在线优化结果如表1所示，控制参数迭代过程如图2～图4所示。

表1 控制参数在线优化结果Tab.1 Online optimization results

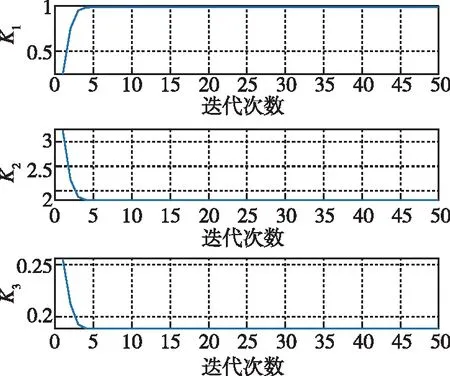
图2 无弹性体RADP参数迭代结果Fig.2 Parameter iteration results of RADP without elastic vibration

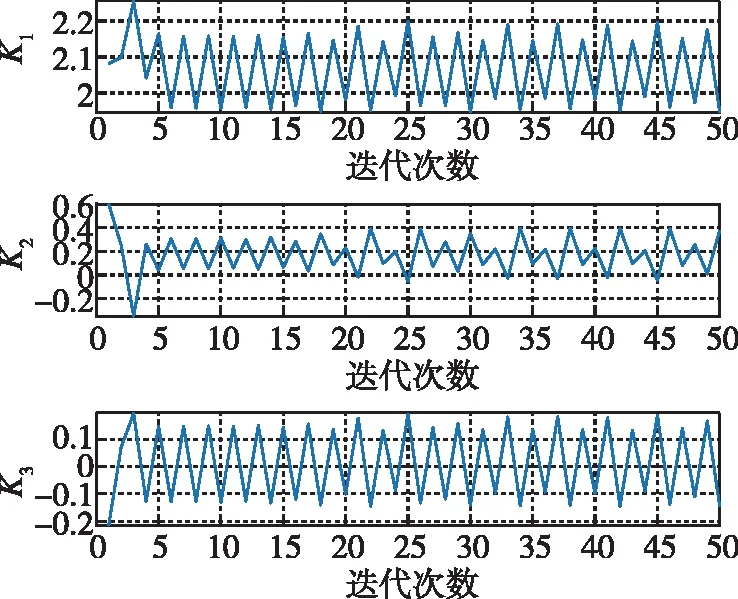
图3 不加滤波器RADP参数迭代结果Fig.3 Parameter iteration results of RADP without filter

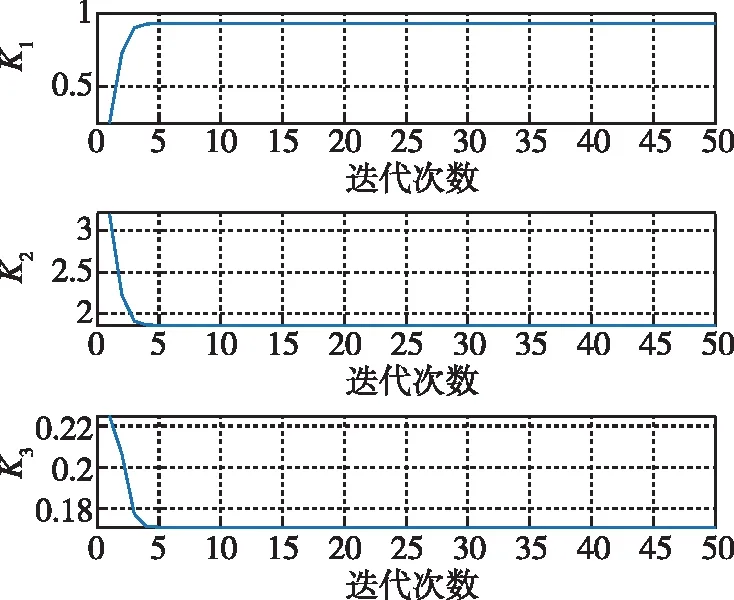
图4 加滤波器RADP参数迭代结果Fig.4 Parameter iteration results of RADP with filter

仿真对比曲线如图5～图7所示。

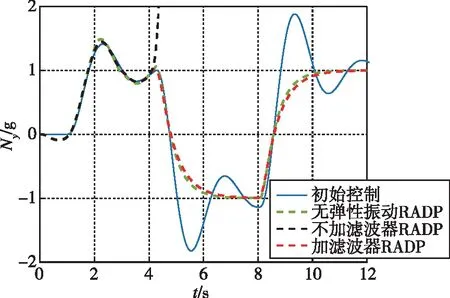
图5 过载跟踪曲线Fig.5 Overload tracking curve

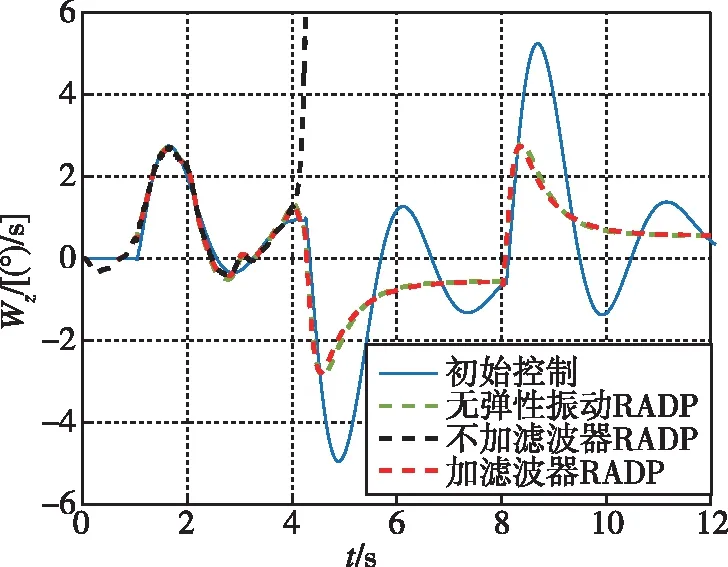
图6 角速度变化曲线Fig.6 Angular velocity variation curve

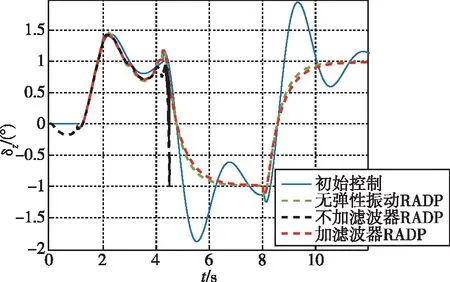
图7 舵偏变化曲线Fig.7 Rudder deviation curve

从图中可以看出，在初始控制参数的作用下，过载响应、角速度和舵偏出现较明显的振荡，过载跟踪超调接近50%。仿真中在4s左右进行控制参数在线更新，参数迭代过程如图2～图4所示，更新后的控制参数如表1所示，当采用不加滤波器的RADP方法时，迭代参数不收敛，且更新后控制参数与解析解差异很大，表明RADP方法解算准确性明显受到弹性振动影响，当采用本文加滤波器的RADP方法时，迭代参数迅速收敛，且更新后控制参数与解析解基本一致，表明本方法较好地隔离了弹性振动的影响，有效提高了控制参数在线优化的准确性。此外，本文所提方法有效提升了控制品质，并保证了过载响应对指令的稳定跟踪。

4 结 论

针对弹性高超声速飞行器过载跟踪控制性能在线优化和振动影响下的控制参数准确更新问题，提出了一种基于数据驱动的弹性高超声速飞行器过载跟踪自学习控制方法。算法分析与实验结果表明，在不依赖于准确模型参数的条件下，所提的方法能够有效实现弹性振动干扰下的控制参数在线优化，并提高过载跟踪控制品质。但本文仅是通过数字仿真完成了相关验证工作，后续将通过半实物仿真进一步验证算法的适应性。