基于人工智能的深潜耐压球壳应力场映射

姚骥，汪雪良，叶聪，顾学康，孙梦丹，蒋镇涛

（1.中国船舶科学研究中心，江苏 无锡 214082；2.深海技术科学太湖实验室，江苏 无锡 214082）

深潜耐压球壳是载人深潜器的核心部件，其结构安全是确保潜器顺利完成水下任务的前提，因此对其结构健康状态的实时监测十分重要。当前，由于安全条件、空间分布等限制，仅能对有限测点的应力信息进行实时监测，无法直接获取深潜耐压球壳全局应力场信息。因此，亟需开展利用有限测点信息，间接测量全局应力场信息的研究。

目前，许多学者针对深潜耐压球壳结构的安全性与承载能力开展了大量研究。其中，挪威船级社（DNV）[1]、法国船级社（BV）[2]、美国船级社（ABS）[3]、俄罗斯船级社（RS）[4]和中国船级社（CCS）[5]均对载人舱球壳的承载能力设计进行了要求，要求极限承载能力至少应为最大工作压力的1.5 倍以上[6]。张磊等[7]对不同计算公式的计算结果进行了对比，发现各公式预测结果与实验破坏压力均存在偏差。杨露等[8]通过实验和数值计算方法，对大深度载人舱长期寿命评估中的影响因素开展了研究。王芳等[9-13]针对大深度载人潜器疲劳问题开展了研究，并在结构退化规律、疲劳寿命预测等方面取得了相关成果。王丹等[14]针对载人舱球壳本身初始形状对其临界载荷的影响开展了研究，并给出了计算表达式。杨华伟等[15]为保障载人舱球壳结构安全，开展了载人舱结构健康监测评估系统设计研究，并给出了结构安全性评估算法函数。在应力场监测与映射方面，李卿汉等[16]针对船海结构疲劳失效的问题，设计了一种基于应力测量和响应技术的船舶结构可靠性监测系统。周天宸等[17]利用BP 神经网络和粒子群算法提出了一种船舶结构应力监测数据处理与异常诊断算法。姚骥等[18]利用人工智能方法提出了一种张力腿结构全局变形场映射方法。张涛等[19]以海洋平台某连接器结构为研究对象，提出了一种基于BP 神经网络的应力场求解方法，该方法求解精度达到93.6%。Kefal 等[20-21]运用逆有限元法对船舶结构典型位置的全局应力和弯矩进行了计算。张宏等[22]基于BP 神经网络和粒子群算法，提出了一种油气管道二维应力分布的机理模型。李成等[23]对不同荷载作用下圆孔板孔边及孔口附近应力场开展了仿真分析，并建立了基于弹性理论及复变函数理论的计算模型。白茉莉等[24]基于复变函数方法，结合计算软件的符号运算系统对椭圆形孔口周围应力场进行了推导，并给出了全空间应力场的解析表达式。综上所述，当前对于深潜耐压球壳全局应力场映射研究较少。

围绕深潜耐压球壳全局应力场实时映射这一核心问题，本文提出一种基于人工智能的深潜耐压球壳应力场映射模型。首先，基于球壳设计参数、建造过程数据、模型试验数据，构建深潜耐压球壳有限元模型，并开展仿真分析。其次，综合考虑应力分布形式、相互独立性、安装条件等因素，提出深潜耐压球壳监测布点方案。然后利用长短时记忆神经网络（Long-short Term Memory Network，LSTM），将测点应力信息作为输入，将全局应力场信息作为输出，构建了深潜耐压球壳应力场映射模型，并与其他神经网络方法进行对比。最后，对不同测点数量下的映射精度进行了验证。

1 深潜耐压球壳简介与仿真分析

1.1 深潜耐压球壳

深潜耐压球壳主要由球壳、开口1 及开口2 等部件组成，如图1 所示。在长期服役过程中，经常在工作深度范围内上浮和下潜。当深度发生变化时，球壳承受的外部压力也不断变化。因此，对其结构状态的实时监测十分重要。

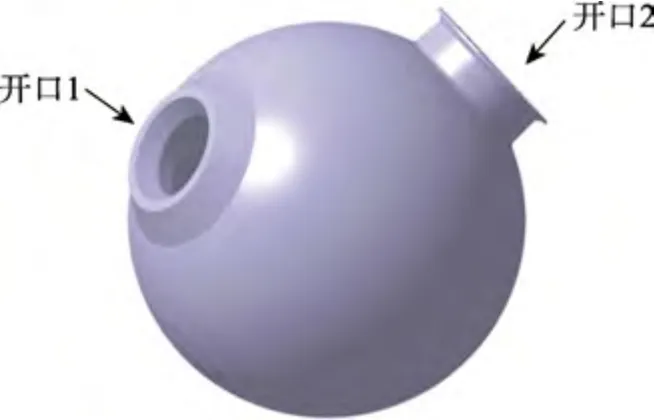
图1 深潜耐压球壳示意图Fig.1 Schematic diagram of deep-sea pressurized spherical shell

深潜耐压球壳主要由高性能钛合金组成，该材料具备屈强比高、潜深大、服役年限长、下潜往复次数多等显著特征。表1 给出了深潜耐压球壳的相关参数，其中厚度t的计算见式（1）—（3）。

表1 深潜耐压球壳结构参数Tab.1 Structural parameters of deep-sea pressurized spherical shell

式中：Pj为计算载荷；R为球壳内部半径，取396 mm。因此，球壳厚度t=33.33 mm。为安全考虑，t取35 mm。

1.2 深潜耐压球壳仿真分析

深潜耐压球壳在长期服役过程中，主要承受静水压力的作用。因此，利用有限元方法构建深潜耐压球壳仿真模型，其中开口1 与开口2 处采用等效载荷方式。其次，根据中国船级社《潜水系统和潜水器入级规范》要求，采用3 点约束的方式，约束6 个位移分量，边界条件对称设置，即在壳体位于x和z坐标轴的位置上（相隔90°）取3 个节点：在z轴上的节点1 和2，其ux=uy=0；在x轴上的节点3，其uy=uz=0。

深潜耐压球壳有限元仿真结果如图2 所示，其中仿真模型选用六面体单元，网格尺寸为2 cm。可以看出，在开口1 与开口2 处均存在高应力区。同时，球壳典型位置处应力分布较为均匀。

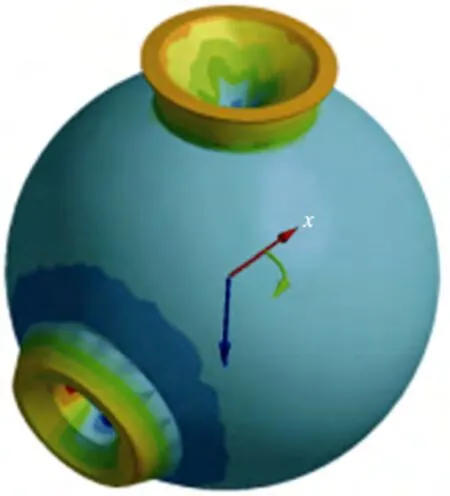
图2 深潜耐压球壳有限元仿真云图Fig.2 Simulation cloud map of deep-sea pressurized spherical shell

将仿真结果与模型试验结果进行对比，结果见表2。可以看出，最大误差仅为1.92%。说明有限元分析结果较为准确，可为深潜耐压球壳应力场映射算法提供数据支撑。

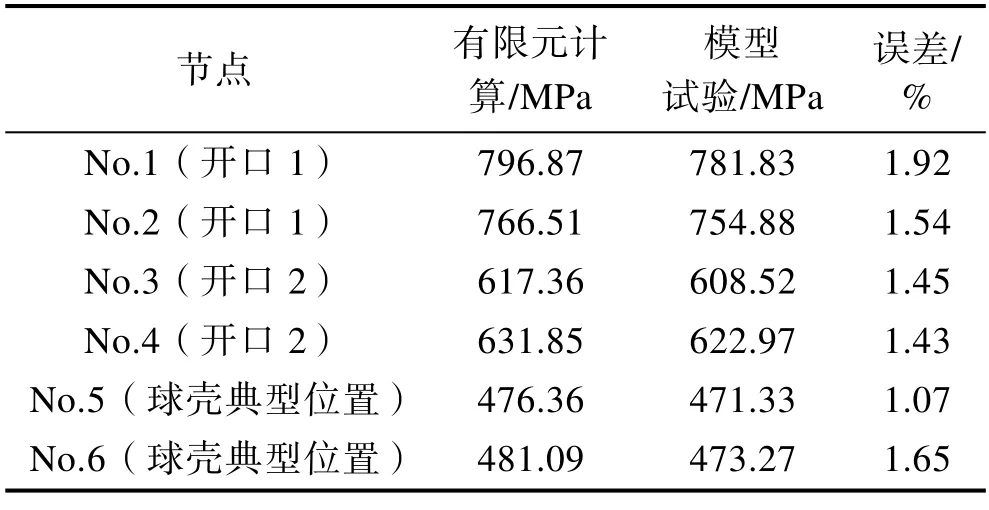
表2 仿真结果与试验结果对比Tab.2 Comparison between simulation results and experimental results

1.3 监测布点方案决策

深海耐压球壳应力场成因复杂，影响因素多，现有测量手段往往只能反映局部应力的信息。综合考虑应力分布形式、相互独立性、安装条件等因素，在开口1、开口2 等高应力区位置及赤道焊缝处各选取8 个测点，球壳典型位置处选取6 个测点。利用人工智能方法，构建测点应力与全局应力场的映射关系模型。

2 应力场映射算法研究

2.1 数据集选取

选取载荷步为0.1 MPa，对设计载荷（100 MPa）进行划分，并开展有限元仿真，共仿真1 000 个工况。将测点应力作为输入，将全局应力场作为输出，构建球壳应力场映射模型。此外，训练集、交叉验证集与检验集的比例分别为70%、15%、15%。应力场影响映射算法数据集选取见表3。

表3 数据集选取Tab.3 Selection of datasets

2.2 长短时记忆神经网络（Long-short Term Memory Network，LSTM）

与标准神经网络相比，循环神经网络是以序列数据为输入、在序列演进方向进行递归，且所有节点按链式连接的递归神经网络，可将上一个状态的信息传递到当前状态。当输出为时间序列时，可以将其展开为一系列相互连接的标准神经元。LSTM 神经网络是循环神经网络的一种，用以解决一般循环神经网络中存在的长期依赖问题。LSTM 神经网络结构由Hohreiter 和Schmidhuber 于1997 年提出[25]，是一种特殊的循环神经网络，由一系列LSTM 元组成，如图3 所示。

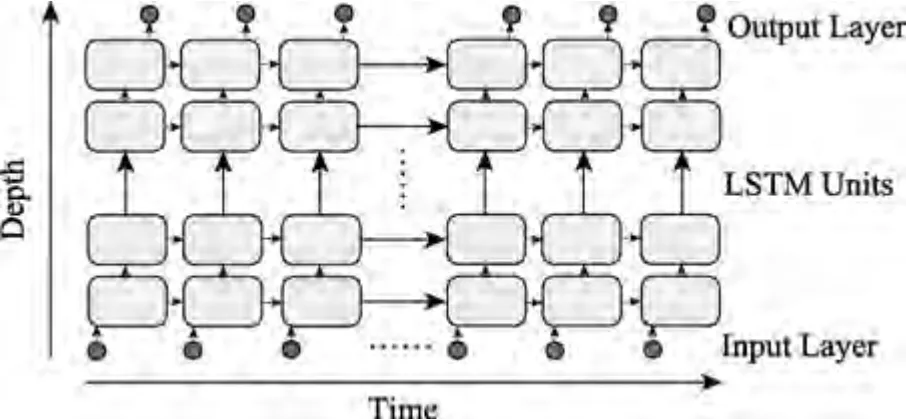
图3 LSTM 结构Fig.3 LSTM structure

LSTM 元包括新输入xt、输出ht、输入门it、忘记门ft、输出门ot，如图4 所示。引入输入门、忘记门与输出门的目的是控制每一步输出的值，使得误差在该神经元传递过程中保持不变。LSTM 是循环神经网络的一个特例，新输入和每个门都会将前一次的输出ht－1作为本次输入的一部分。因此，新输入xt、输入门it、忘记门ft、输出门ot的输入都是由[xt,ht－1]二元组构成。

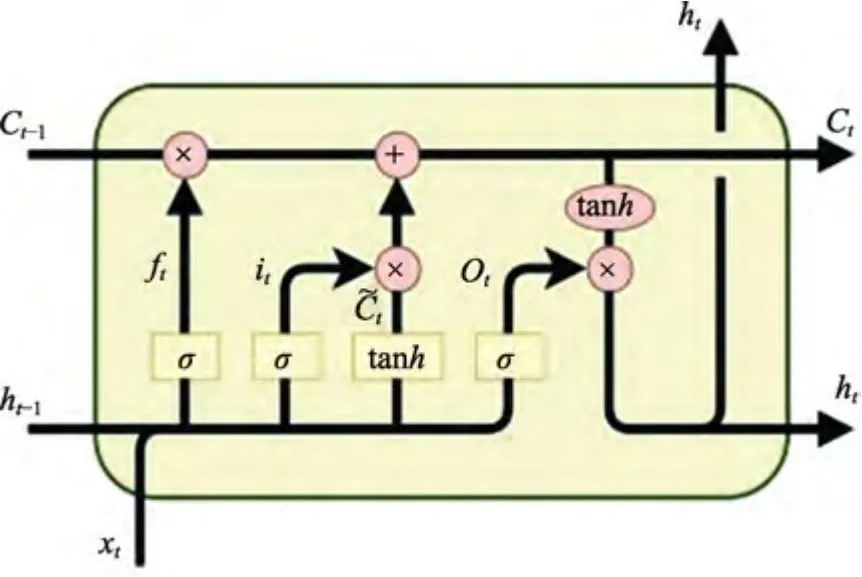
图4 LSTM 循环体结构Fig.4 LSTM loop structure

新输入[xt,ht－1]经过激活函数σc作用后，得到记忆元的候选值Ct：

式中：Wc表示连接权；bc表示激活函数的一个激活阀值。

输入门用于调整候选值Ct的大小，输入门的输出为：

式中：Wi表示连接权；bi表示激活函数的一个激活阀值。候选值Ct经过输入门的调整，其值为Ct·it。

忘记门用于控制LSTM 元的记忆状态St－1，忘记门的输出为：

式中：Wf表示连接权；bf表示激活函数的一个阀值。记忆状态St－1经过忘记门的调整，其值为ft·St－1。

此时，t时刻的状态St由其所记忆的前一时刻状态St－1和状态更新的候选值加权得到:

输出门ot当作状态St最终输出的一个权值，控制状态St的输出大小，输出门的公式为：

最终LSTM 元的输出为：

式中：σc、σi、σf、σo、σs为激活函数。

2.3 建模过程

LSTM 应力场映射模型如图5 所示。整个深度学习模型共包括6 层，其中LSTM 层数为2，每层节点数为10，全连接层数为2，节点数为10，最后一层作为输出层。采用均方根误差作为代价函数，训练次数为1 000。

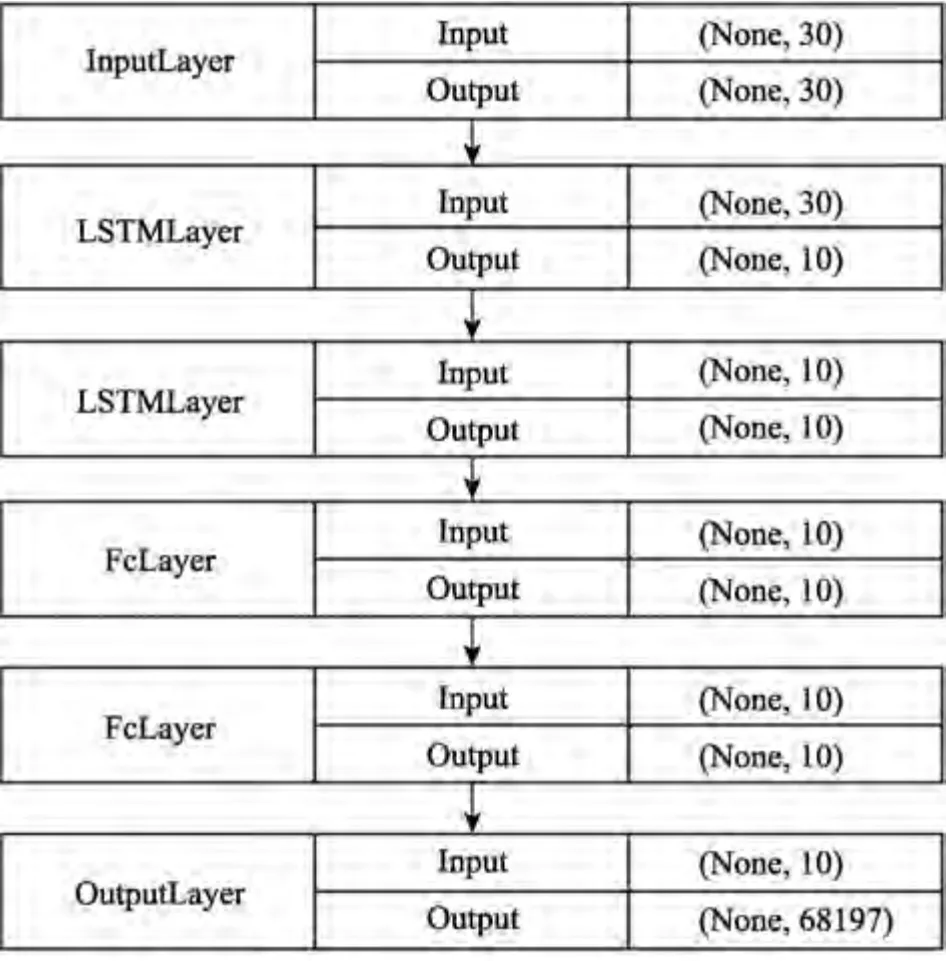
图5 应力场映射模型Fig.5 Stress field mapping model

3 结果分析与讨论

3.1 映射结果分析

深海耐压球壳应力场映射算法的训练过程如图6所示。可以看出，随着训练次数的增加，训练损失值与交叉验证损失值降低，两者具备较好的一致性。同时，训练均方根误差与交叉验证均方根误差随着训练次数的增加而降低。在训练完成时，训练损失值为2.42，交叉验证损失值为9.44，训练均方根误差为2.20，交叉验证均方根误差为4.34。

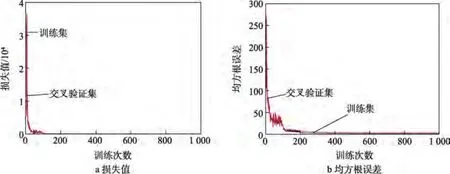
图6 训练过程Fig.6 Training process:a) loss;b) RMSE

不同深度下全局应力场的映射结果如图7 所示，其中下潜深度选取1 000、4 000、7 000、10 000 m。可以看出，在下潜深度较小时，映射结果与期望结果存在一定的偏差，其线性拟合斜率为0.99，接近于1。当下潜深度增大时，映射结果与期望结果具备较好的一致性，其线性拟合斜率均为1。相比应力场变化范围，其在y轴上的截距较小，进而说明本文所提深潜耐压球壳应力场映射算法具备较好的映射精度。

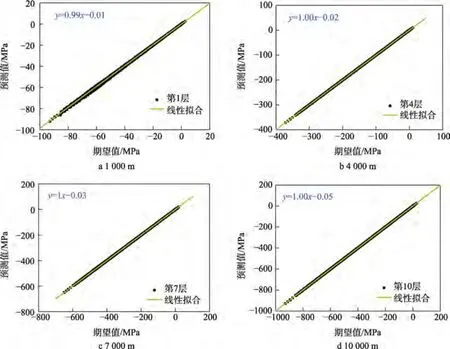
图7 不同下潜深度的映射结果Fig.7 Mapping results of different diving depths

为了进一步分析LSTM 模型的映射准确率，图8给出了所提模型的映射残差Rs：

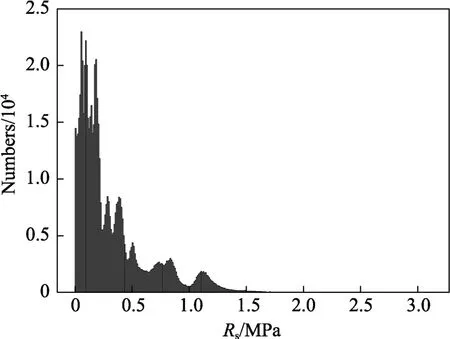
图8 映射残差分布Fig.8 Distribution of mapping residual error

可以看出，映射残差大多分布在0～0.5 MPa。相比于应力场的变化范围，映射残差极小。

为了定量分析所提模型的映射误差，选取平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）ηMAPE作为评价指标：

深潜耐压球壳应力场映射模型的映射误差（±表示偏差方向）如图9 所示。可以看出，在下潜深度较小时，映射结果与期望结果相对误差为－1.49%。当下潜深度增大时，映射误差较小，均小于0.5%。在下潜深度为10 000 m 时，映射误差仅为0.05%。映射结果表明，本文所提深潜耐压球壳应力场映射算法可对其下潜过程中的全局应力场进行准确映射，并具备较高精度。

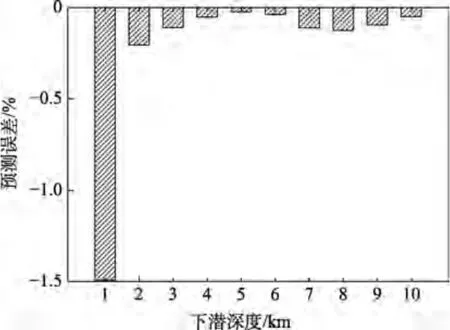
图9 不同下潜深度的映射误差Fig.9 Mapping error under different diving depths

此外，利用相同计算资源（i7-10700CPU@2.9 GHz,32RAM,NVIDIA GeForce RTX 2060）开展研究。有限元模型计算1 个工况平均耗时为1.2 s，而本文所提应力场映射模型计算 1 个工况平均耗时0.019 6 s，计算效率提升约60 倍，为深海耐压球壳在实际服役过程中的应力场实时映射提供支撑。

3.2 不同方法映射结果对比

为了评估本文所提深潜耐压球壳应力场映射算法的精度，选取深度神经网络（Deep Neural Network，DNN）与反向传播算法（Back Propagation，BP）作为对比，构建深潜耐压球壳应力场映射模型。其中DNN 模型隐藏层数为3，各层节点数为30。BP 模型隐藏层数为1，节点数为50。损失函数选取与LSTM模型一致。

不同模型不同下潜深度下的映射结果如图10 所示。可以看出，相比LSTM 模型，DNN 模型与BP模型均存在较大的映射误差。其中，BP 模型在下潜深度较小时，映射结果较差。当下潜深度增加时，映射误差减小。

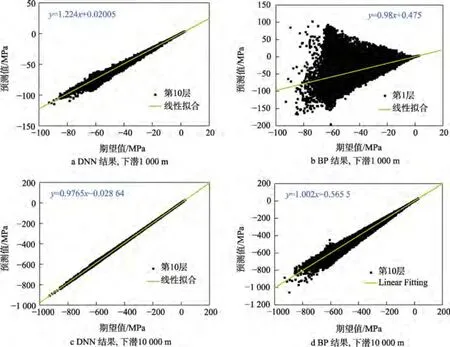
图10 不同模型的映射结果Fig.10 Mapping results of different models:a) DNN results,1 000 m;b) BP results,1 000 m;c) DNN results,10 000 m;d) BP results,10 000 m

为了定量分析不同模型的映射精度，图11 给出了不同模型不同下潜深度下的映射误差。可以看出，BP 模型的映射误差最大，在下潜深度较小时达到了50%以上；DNN 模型的映射误差小于BP 模型，大于LSTM 模型，在下潜深度较小时达到20%以上；LSTM 模型映射误差最小，且远小于DNN 模型与BP 模型。

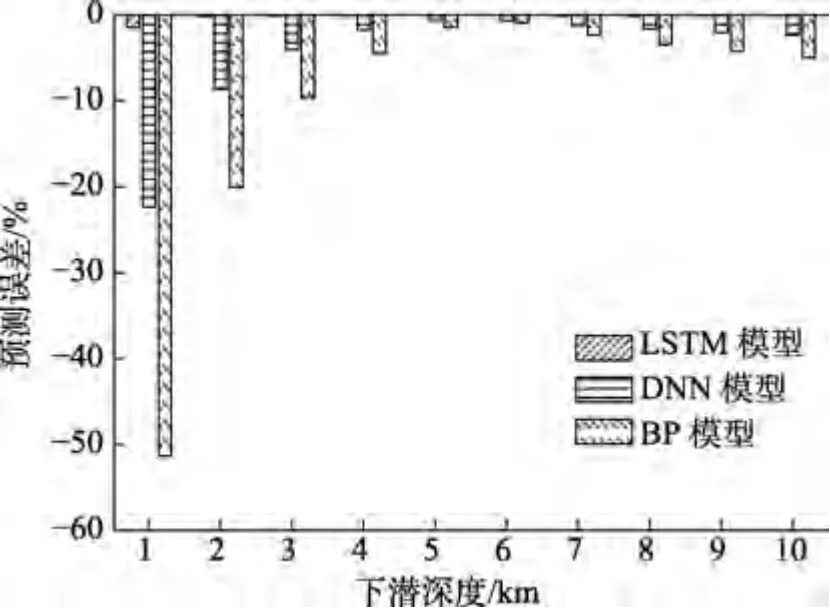
图11 不同模型不同下潜深度映射误差Fig.11 Mapping errors of different models under different diving depths

由不同模型的映射误差可知，LSTM 模型的平均映射误差为0.23%，相比于DNN 模型与BP 模型的4.53%和 10.30%，映射误差分别下降 94.92%与97.76%。这进一步说明了本文所提模型可对实际下潜过程中深潜耐压球壳全局应力场进行实时映射。

3.3 不同监测数量下的映射结果

在深潜耐压球壳长期服役过程中，传感器容易发生机械故障，导致设备失效。此外，失效点存在随机性。因此，采用随机丢失的方式，选取监测点数量为5、10、15、20、25、30（无丢失），利用所提深潜耐压球壳应力场映射算法，构建不同监测数量下的耐压球壳应力场映射模型。

不同监测数量下，相同下潜深度（10 000 m）的映射结果如图12 所示。可以看出，在所选监测数量（5、10、15、20、25、30）下，各映射模型的映射结果与实测结果均保持较好的一致性，其线性拟合斜率均为1。同时，相比应力场变化范围，其在y轴上的斜率较小。

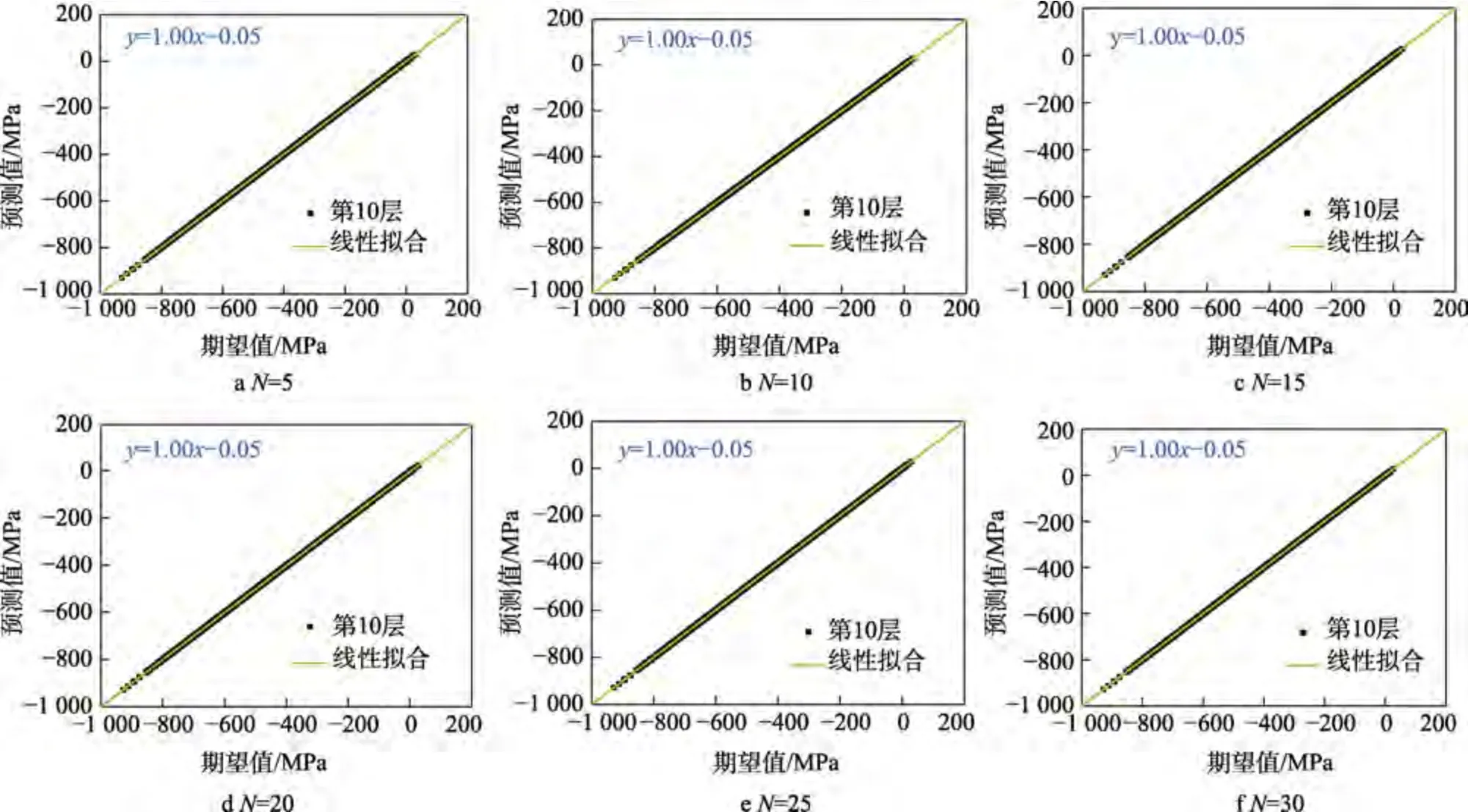
图12 不同监测数量下的映射结果Fig.12 The mapping results of different monitoring locations

为了定量分析不同模型在不同下潜深度时的映射结果，图13 给出不同监测数量下各模型在不同下潜深度下的映射误差。可以看出，在下潜深度较小时，各模型的映射误差较大，但也均小于1.5%。在下潜深度较大时，各模型映射误差均小于0.5%。

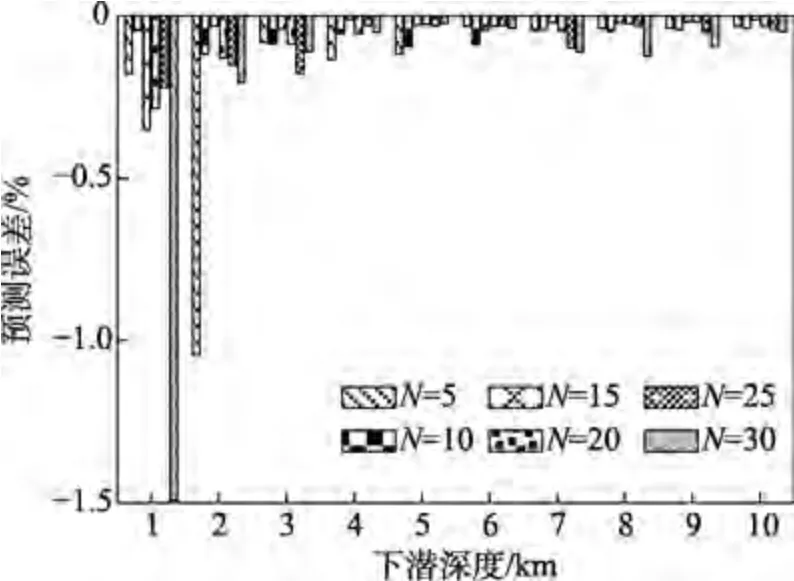
图13 不同监测点下不同深度的映射误差Fig.13 The mapping results of different depths of different monitoring locations

由不同监测数量下的映射误差可以看出，监测数量为5 时，映射误差为0.17%，监测数量为30 时，映射误差为 0.23%，所提模型的映射误差均小于0.5%。所提深潜耐压球壳应力场映射算法可在测点存在部分失效的情况下仍取得较高的映射精度，同时验证了所提监测布点方案具备监测冗余性。

4 结论

本文提出一种基于人工智能的深潜耐压球壳应力场映射算法，解决了实际下潜过程中全力应力场难以获取的问题，也为耐压结构受力状态全方位监测提供新的思路。主要结论如下：

1）基于深潜耐压球壳建造过程数据，建立高保真的有限元模型，并与模型试验数据进行对比，最大误差仅为1.92%。给出了深海耐压球壳应力监测方案。

2）基于LSTM 网络，构建深潜耐压球壳应力场映射模型。从映射结果可以看出，其全局应力场最大误差仅为1.49%。与有限元仿真计算相比，所提方法的计算效率提升约60 倍。

3）针对实际服役过程中潜在的传感器失效风险，采用随机丢失的方式，对不同监测数量的映射模型进行分析。所提方法平均误差均小于0.5%。