基于实船结构监测数据的异常检测及处理方法

2023-10-18孙梦丹汪雪良吴国庆姚骥蒋镇涛

装备环境工程 2023年9期

孙梦丹，汪雪良，吴国庆，姚骥，蒋镇涛

（中国船舶科学研究中心,江苏无锡 214082）

为适应世界海运发展，加强海洋资源开发，船舶技术发展尤为重要。张凤梅等[1]提出，我国是一个海洋大国，对海洋科学装置与相关产业技术创新的研究亟待深入。船舶行驶在复杂的海域环境中，易受到波浪激励、设备振动、电磁干扰等环境因素的影响，造成船舶结构损坏。汪雪良等[2-4]从理论预报、模型试验和实船测试3 个方面，针对波浪激励、设备振动对船舶的影响展开了研究。徐春等[5-6]针对船体波激振动的响应特征，采用小波预报、傅里叶变换的方式进行分析和处理。周天宸等[7]提出，需要建立实时监测船体健康的系统，从结构应力监测数据角度对船体结构进行故障识别与诊断。因此，需要建立船体状态实时监测系统，收集船舶在行驶中的数据，分析并判断船舶行驶状态下存在的问题，以保障航行安全。实船结构监测数据通过在船上布放传感器获取，郑庆新等[8]针对应用于船舶结构安全监测的应变传感器开展了研究，提出了严格的技术规定。然而，直接获得的数据往往含有异常现象，影响统计分析的客观性。

综上所述，船舶在行驶过程中易受到外界环境因素干扰，造成结构失效等不良影响。因此，为开展船体结构安全分析，需开发船体结构监测系统，获取船舶在行驶中的结构应力数据。然而，直接获取的监测数据往往含有异常现象，现针对真实海况下船舶结构应力数据存在的异常现象，开发数据异常处理算法，为开展后续船体结构安全分析提供数据输入。

1 信号异常分析及处理方法

1.1 信号异常分析

针对某实船结构应力数据，选取一段含有典型异常现象的4 h 信号作为分析对象。信号原始图像如图1 所示。由图像分析可得，信号中存在的典型异常现象为信号跳变，即信号中存在离群值。离群值是指数据中与其他值明显不同的异常值，可能由于数据损坏或错误导致，也可能由于真实数据的异常情况导致[9]。Mandhare 等[10]开展了基于聚类、距离、密度等一系列离散值的监测技术研究。徐鹏涛等[11]针对数据中离群值的处理，开展了卷积神经网络模型训练等一系列方法研究。本目标案例中存在的信号离群值是由设备振动、电磁干扰、波浪激励等外界干扰因素造成的，与正常数据段中信号特征有显著差异。为避免对后续船舶结构特征分析造成误差影响，故研究异常值处理算法，对真实海况下船舶结构应力数据存在的信号异常跳变现象进行去除。

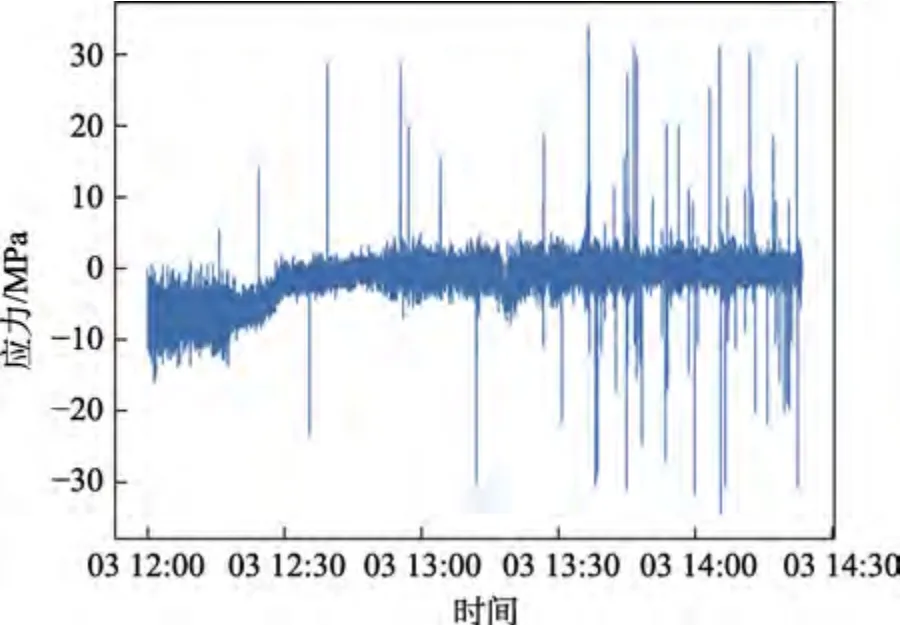
图1 信号原始图像Fig.1 Original signal image

1.2 信号异常处理方法

本文针对3 种信号异常处理方法开展研究，分别为Hampel 滤波法、Smooth 平滑函数法和Z-score 异常检测及平均值异常处理法。

1.2.1 Hampel 滤波法

Hampel 滤波法是一种基于决策的滤波法，通过该滤波法可以找到数据序列中的异常数据点，以更有代表性的数值替换，如滤波法移动窗口中的短序列的中值[12]。李麒等[13]基于Hampel 滤波法，针对某土石坝渗流压力原始监测数据进行识别粗差处理，证明Hampel 能在不获取数据完整趋势的情况下进行判断，具有良好实时性和识别效果。常见的Hampel 滤波法通过中位数进行离群值检测，并消除数据中存在的离群值。

对于数据序列a1,a2,…,ai设定每个样本ai两边的样本数量l，则滑动窗口长2l+1，窗口样本中值可表示为：

为验证窗口选取值对Hampel 处理精度的影响，分别选取窗口样本数为1、2、3、5、7。验证数据为同一组原始信号及其加跳变现象后生成的异常数据。通过不同窗口样本数的Hampel 滤波法对异常数据做处理，求处理误差，结果见表1。

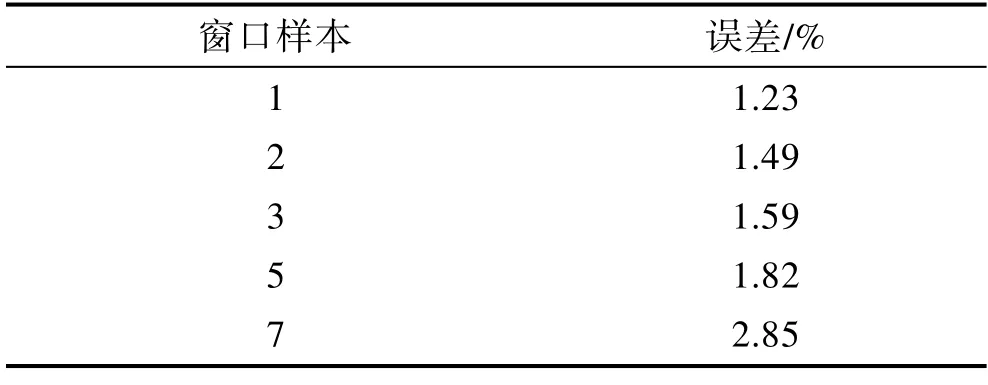
表1 不同窗口样本数的异常处理误差Tab.1 Anomaly processing error for different window sample sizes

由误差结果可得，窗口样本越少，异常处理的误差越小。已知随着窗口样本数减少，运行时间增长。综合考虑异常处理误差及运行时间，选取3 作为窗口样本数。

绝对中位差的定义为，用原数据减去中位数后得到的新数据的绝对值的中位数，常用来估计标准差。由CNAS-GL002:2018[14]算法A 可知，标准差=1.483×绝对中位差。窗口样本的标准差的计算见式（2）。

GB/T 28043—2019/ISO 13528:2015[15]规定，能力验证结果的评价一般应包括指定值的确定、能力统计量的计算、能力评定。其中能力统计量（z值）在国内外各项能力验证计划中得到了广泛应用，能力验证结果xi的z值（即zi）可以采用式（3）计算。

式中：xi为实验室测定结果；xpt为指定值；σpt为能力评定标准差。以z值评价参加能力验证计划各实验室的结果：当|z|≤2.0，表明结果可接受；当2.0<|z|<3.0，给出警戒信号；当|z|≥3.0，结果不可接受（或给出行动信号）[16]。

在本方法中，xi为窗口内某值，xpt为窗口中值，σpt为ei。如果窗口内某个值大于3 倍中值绝对偏差ei，则将其判定为离群点，并由窗口中值代替。

新生成的窗口数据序列bi可表示为：

1.2.2 Smooth 平滑函数

Smooth 函数是一种常用的数学函数，其基本原理为使用滑动平均滤波算法，对每一个数据进行卷积运算，采用卷积算子模拟线性非时变系统对信号的影响，使之趋于一定数值[17]。Yuan 等[18]、Bai 等[19]利用Smooth 函数，针对超声波探伤仪、风电场等不同领域的输出信号中存在的噪声或平滑不连续现象，开展了信号平滑处理，取得了显著效果，证实了Smooth函数在研究中的信号优化作用。

滑动平均滤波法原理为，将连续取的N个采样值看成一个队列，队列的长度固定为N，每次采样到一个新数据放入队尾，就扔掉原来队首的一次数据（先进先出原则）。把队列中的N个数据进行算术平均运算，获得新的滤波结果[20]。

Smooth 函数计算类似一维卷积的工作原理，使滑动平均滤波法的N对应一维卷积核大小（长度）。进行算术平均运算时，一维卷积核大小（长度）和N相等，步长设置为1，核参数初始为1，沿着输入滑动窗口并计算窗口内容的平均值[20]，获得滤波结果。由于一维卷积计算速度快，Smooth 函数可高效地实现异常信号消除功能。

1.2.3 Z-score 异常检测及平均值异常处理

在传统信号异常处理方法外，结合统计学异常检测方法与常见数据异常值去除方法开发效果更好的信号跳变处理方案。

首先采用统计学中的Z-score 异常检测方法，识别信号存在的跳变现象。Z-score 是一维或低维特征空间中的参数异常监测方法[21]。唐瑜婕等[22]、Ismail等[23]、韩霞等[24]分别使用Z-score 数据异常检测方法针对企业财务、马来西亚产品质量、文献引用等不同领域数据进行异常值检测，证实了Z-score 异常检测法在信号离群值方面的识别效果。该方法假定数据是高斯分布，异常值是分布在尾部的数据点，因此远离数据的平均值。距离的远近取决于使用公式计算的归一化数据点Zi的设定阈值Zthr：

式中：xi是一个数据点；μ是所有点xi的平均值；σ是xi的标准偏差。

经过标准化处理后，Zi的绝对值大于Zthr的点判断为异常值[25]。根据上述能力统计量（z值）规定，选择异常值参数为3。

为避免异常检测过度，防止正常信号被剔除，此处阈值为3。信号异常识别结果见图2，图中圆点为异常点。最后，使用数据处理中的平均值法去除上述信号跳变。计算异常点前后20 个数据的平均值，作为异常点的新值。

图2 Z-score 异常检测结果Fig.2 Z-score signal anomaly detection results

2 异常处理结果及分析

为验证不同信号处理方法的准确性，首先，采用3 种方法处理同一组异常数据，初步判断信号的处理效果。其次，创建验证数据，从差值角度判断3 种异常处理方法的准确性。最后，基于各组异常处理后数据，计算其对应的结构信号统计值，并与正常数据的统计值作比对，进一步说明异常处理方案在结构监测数据数值统计上的意义。

2.1 异常处理结果

首先，分别使用Hampel 滤波法、Smooth 平滑函数法、Z-score 异常检测及平均值异常处理法处理同一组异常数据，即1.1 小节中展示的某船4 h 异常数据。信号处理结果如图3 所示。由信号处理结果可初步推测，Z-score 异常检测及平均值异常处理法对结构监测数据的异常处理效果最佳。

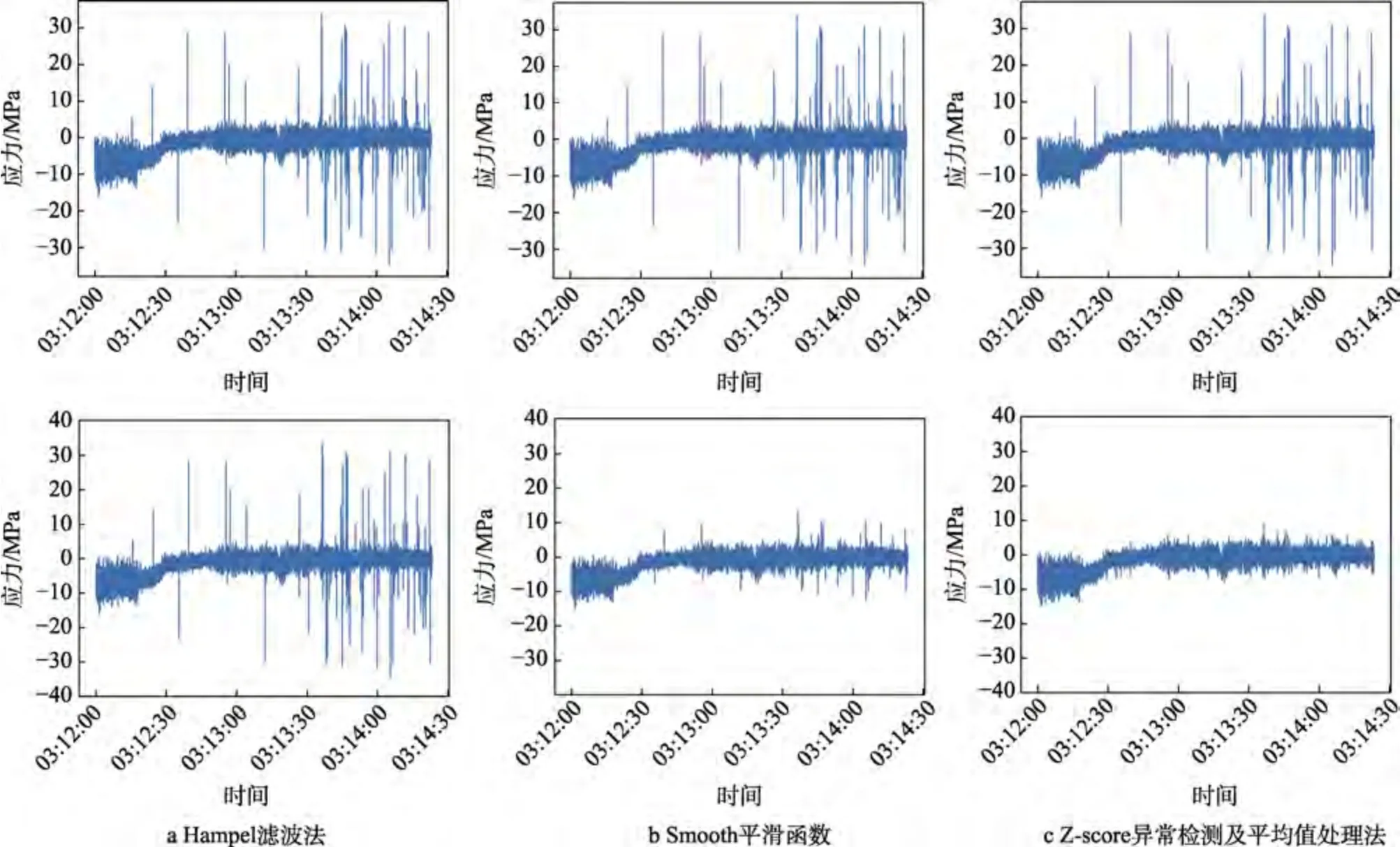
图3 3 种异常处理方法效果对比Fig.3 Comparison of three types of anomaly processing results:a) Hampel filter;b) Smooth function;c) Z-score anomaly detection and average anomaly processing

2.2 实船数据验证

通过实船结构监测数据验证3 种异常处理方法的处理精度。选择一段4 h 信号良好的某实船监测数据，加入同类型信号跳变，获得2 组验证数据。原始数据及两组验证数据如图4 所示。

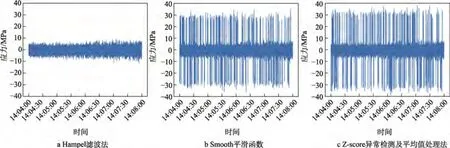
图4 原始数据及验证数据图像Fig.4 Original data and validation data images:a) Hampel filter;b) Smooth function;c) Z-score anomaly detection and average anomaly processing

分别使用3 种异常处理方法处理2 组异常数据，并与原始数据做差值计算，得到如图5 所示2 组差值对比图。

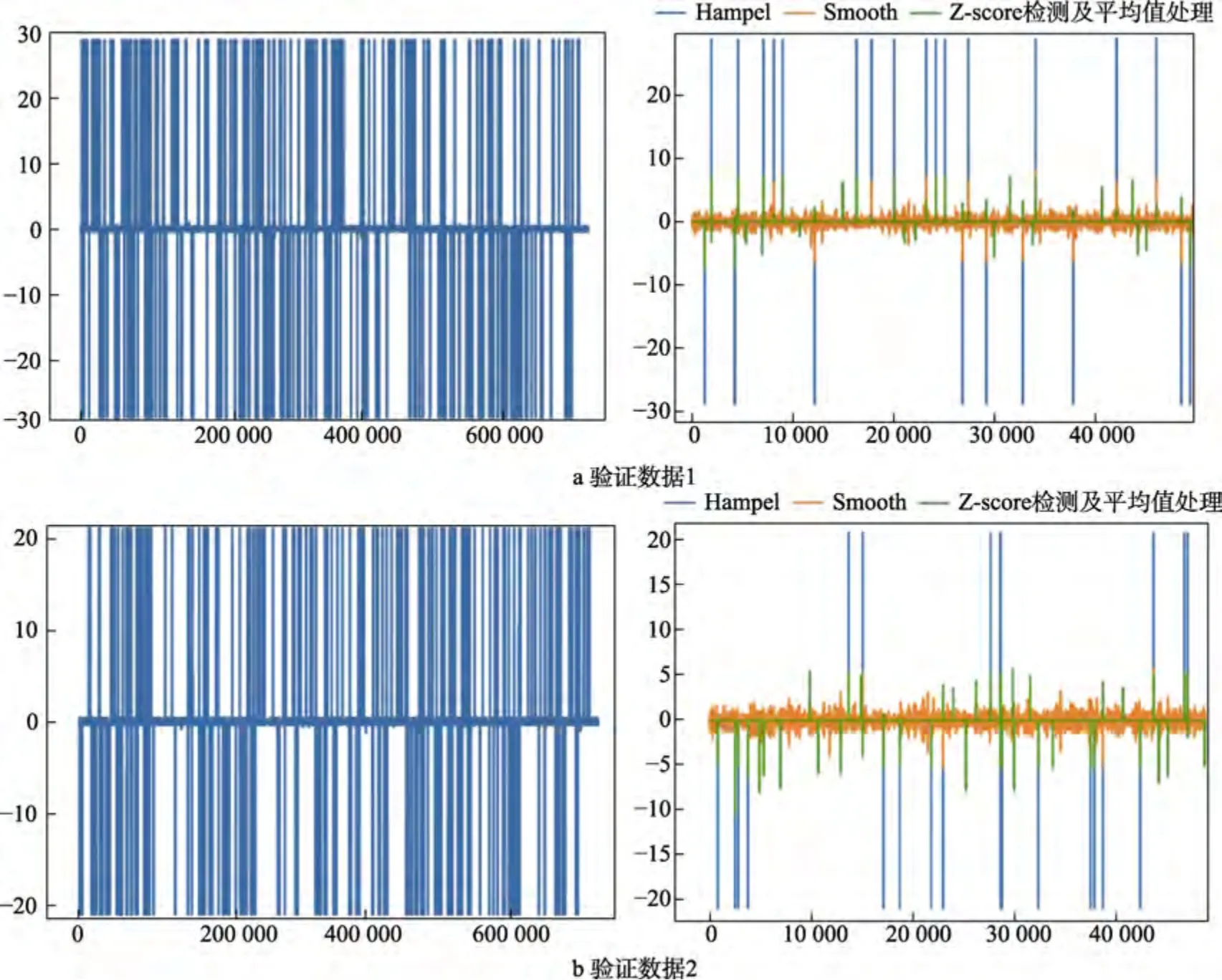
图5 3 种异常处理差值Fig.5 Three types of anomaly processing differences:a) validation data 1;b) validation data 2

由左侧差值对比图可得，Hampel 滤波法对跳变现象的异常处理效果不佳。Smooth 方法与Z-score 异常检测及平均值处理方法均存在少量误差。由右侧放大后的差值对比图可得，经Smooth 方法处理后的数据大量点存在一定程度的误差，Z-score 及平均值方法处理后的数据只有少数点存在一定程度的误差，单点误差程度略大于Smooth 方法。

接下来从工程应用角度，基于传统的结构应力数据处理方法，对比Smooth 方法与Z-score 及平均值异常处理方法的数据处理效果。

2.3 统计值精度验证

在结构应力数据的实际工程应用方面，基于传统的结构应力数据处理方法，通过实验验证Z-score 异常检测及平均值异常处理方法对结构应力数据处理的准确性和计算价值。

在传统的结构应力数据分析方法中，通常采用包括信号滤波、信号成分提取、信号特征值计算的处理方法对结构监测数据进行价值挖掘，生成包括低通、高通、合成3 种信号成分的峰值、谷值、全幅值，并计算其对应的平均值、三一值、最大值，共获得27 个特征值，通过特征值反映船舶结构各部位的受力情况。

现选择一段4 h 不含异常跳变的结构应力数据作为原始数据，并计算其特征值，结果见图6 和表2。

表2 原始数据特征值计算结果Tab.2 Calculation results of original data eigenvalue

图6 原始数据图像Fig.6 Original data images

在正常信号中加入与异常数据同类型的信号跳变，获得3 组验证数据。验证数据如图7 所示。针对3 组验证数据，分别使用3 种信号异常处理方法处理数据，并针对处理后的数据进行特征值计算，特征值对比结果如图8 所示，精度见表3。

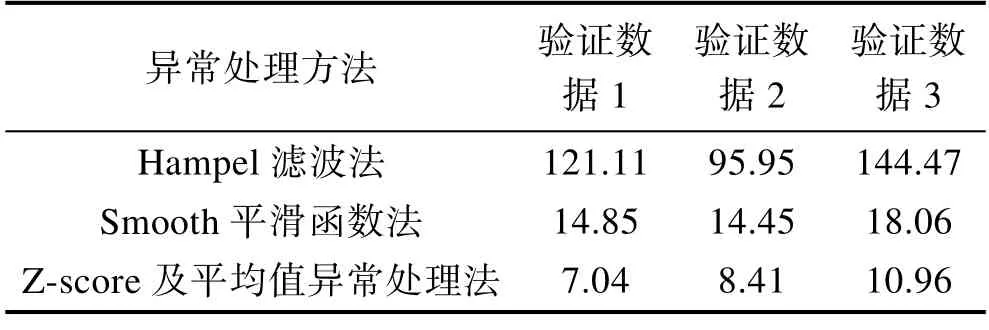
表3 3 种异常处理方法的统计值误差Tab.3 Statistical value error of three anomaly processing methods%

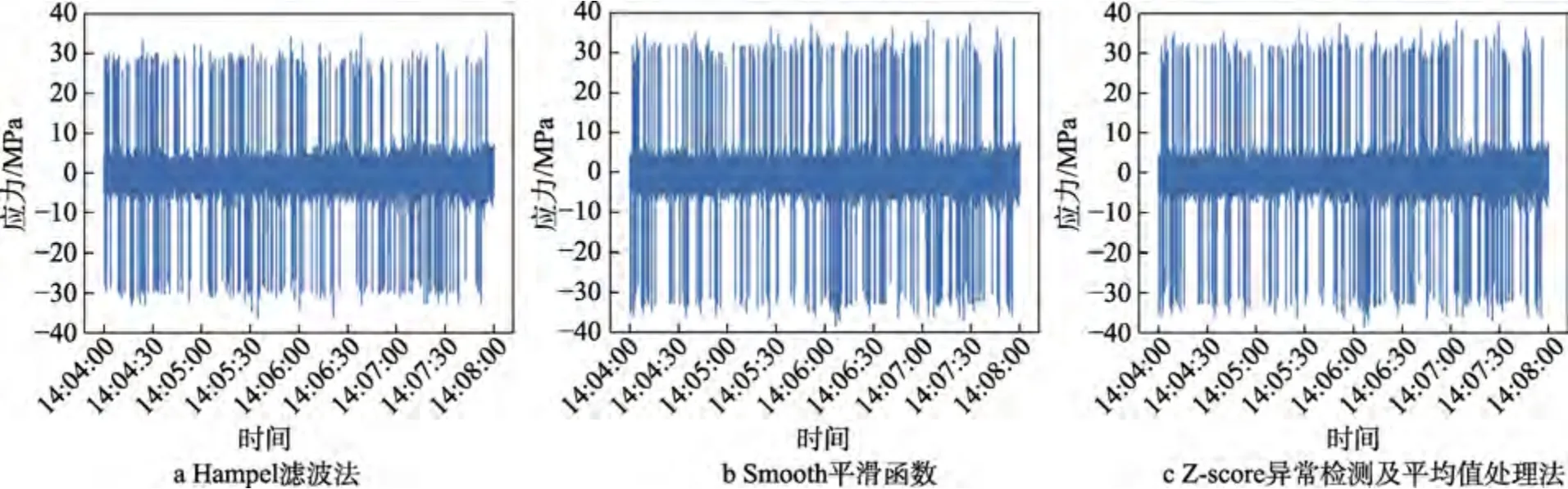
图7 验证数据图像Fig.7 Validation data images:a) Hampel filter;b) Smooth function;c) Z-score anomaly detection and average anomaly processing

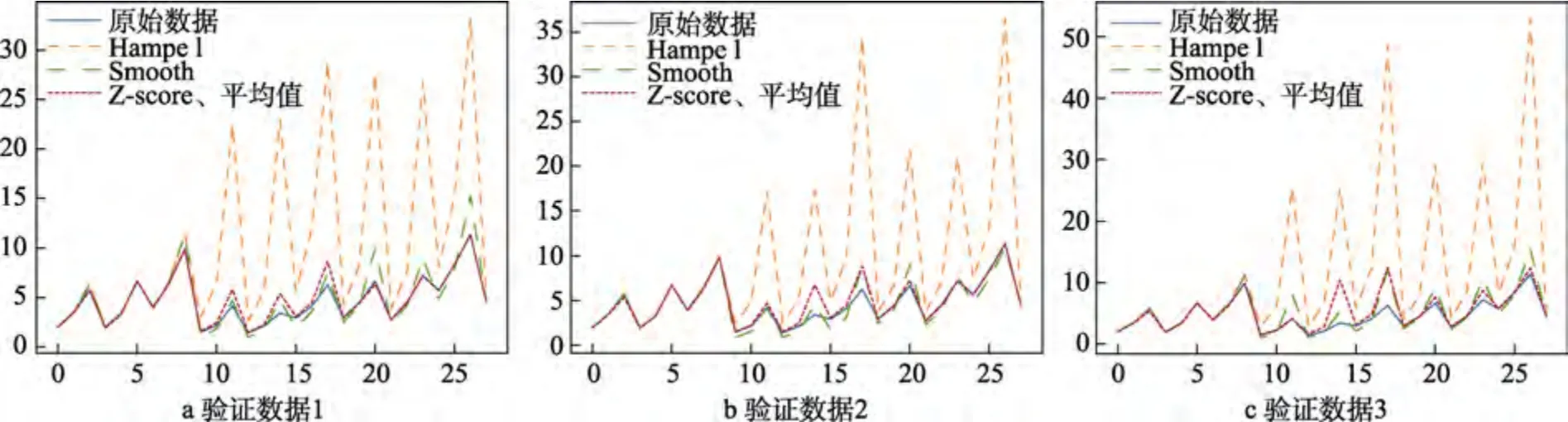
图8 3 种异常处理方法的统计值对比Fig.8 Comparison of statistical values of three anomaly processing methods:a) validation data 1;b) validation data 2;c) validation data 3

由特征值的对比图和误差计算结果可得，由Z-score 异常检测及平均值处理方法处理后的数据获取结构特征值的精度最高，平均精度在90%以上。因此，在Hampel 滤波法、Smooth 平滑函数法、Z-score异常检测及平均值处理方法中，Z-score 异常检测及平均值处理方法针对实船结构应力监测数据存在的异常处现象效果最好。