基于重要抽样法的耐压球壳可靠性计算方法研究

2023-10-18冯士超万正权李艳青

装备环境工程 2023年9期

冯士超，万正权，李艳青

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082；3.深海载人装备国家重点实验室，江苏无锡 214082）

深海载人潜水器[1-3]是进入、探测、开发和保护深海的重要技术手段和装备。载人舱耐压球壳是保证下潜人员及舱内设备免受外界海水巨大压力的耐压结构，是载人潜水器的核心部件[4-5]。目前大深度载人潜水器多选用钛合金耐压球壳形式，其具有结构简单、容重比高、承载能力强、有相同的周向和径向应力值等优点，其质量约占整个潜水器系统的1/5～1/4[6]。载人舱耐压球壳的可靠性水平对整个载人潜水器能够完成设定的任务有决定性影响，同时准确获知耐压球壳的可靠性水平将为开展结构优化设计、减轻结构质量提供重要指导，开展耐压球壳的安全可靠性研究具有重要的意义。

国内学者开展的耐压球壳可靠性评估结果均表明，在工作载荷下，耐压球壳失效是极小概率问题[7-8]，且球壳承载能力的计算属于单失效模式问题。对于失效方程未知的隐式问题，国内外学者在代理模型方法的基础上，对极小失效概率的可靠性求解问题也开展了相关研究。Echard 等[9]提出了一种结合重要抽样和自适应Kriging 方法的能用于处理小失效概率问题的方法，该方法首先需要使用改进一次二阶矩法求得设计点，然后以设计点为中心，建立自适应Kriging 模型，但在计算设计点时，需要使用失效函数对各个变量的偏微分信息，该要求对于隐式问题往往较为困难。Huang 等[10]提出了一种结合子集模拟法和自适应kriging 方法的能处理小失效概率问题的方法，该方法主要是在生成的Kriging 模型基础上，采用子集模拟法计算失效概率。Lv 等[11]提出了一种结合方向抽样和自适应Kriging 方法计算小概率失效问题的方法，该方法是在生成的Kriging 模型基础上，采用方向抽样法计算失效概率。Zhang 等[12]提出了一种基于Kriging 的自适应重要抽样方法，该方法分为2 步，首先通过较稀疏的样本点识别重要抽样中心，然后在重要抽样中心附近建立最终的Kriging 模型。文献[10-12]在计算极小概率失效问题时，均需要设计较大的样本空间用于搜索生成Kriging 模型，但部分Kriging 模型位于失效概率较低的空间，实质上低失效概率空间的Kriging 模型对最终计算结果影响不大，这导致此类方法的计算效率不高，且相关文献中一般均不考虑不同失效条件下的可靠性问题。因此，本文开展了单失效模式下不同失效条件的可靠性问题的计算方法研究。

本文结合自适应Kriging 和重要抽样法，提出了一种用于求解失效条件为非随机变量的极小失效概率问题的重要抽样法。首先，使用自适应Kriging 方法构建较高失效概率下的代理模型，在此基础上获得重要方向，在重要方向上计算得到较低失效概率下的设计点，然后以此设计点为中心，使用自适应Kriging方法构建代理模型，并开展可靠性计算。本文首先通过2 个算例验证了该方法的计算精度与效率，并应用到某耐压球壳结构可靠性计算问题，在获得计算载荷可靠性指标的基础上，计算得到了工作载荷下结构的可靠性指标。

1 自适应Kriging 方法

1.1 Kriging 模型

在可靠性分析中，如果直接采取高精度的仿真模型进行可靠性计算，将产生巨大的计算成本，因此一种以较小计算代价获得研究对象较为准确状态函数的方法——代理模型技术应运而生。代理模型技术[13]就是在保证一定拟合精度的前提下，以某种合适的代理模型方法进行数据拟合，近似获得一个数学函数模型去替代高耗时分析模型进行需要较大样本量的分析工作。Kriging 模型是一种较为常用的构建代理模型的方法。

Kriging 模型的思想由南非采矿工程师Krige 提出[14]。1989 年，Sacks 等[15]将Kriging 理论进一步推广并给出了一种较为实用的 Kriging 算法，使得Kriging 模型在地质、气象、航空航天、船舶等领域得到应用和发展。Kriging 模型一般可表示为一个含参数的线性回归模型和一个随机分布之和，即：

Kriging 模型不仅可以对样本点的函数值进行预测，还能估计预测值的方差，该方差可以用于指导加入新的样本点，以提高建立的代理模型的精度。

1.2 自适应Kriging

为更高效建立Kriging 模型用于开展可靠性分析，自适应Kriging 方法[16-18]被提出并得到了广泛的应用。自适应Kriging 的主要思想是使用学习函数筛选对建立Kriging 模型效果最佳的样本点加入训练样本集，并在此基础上不断更新代理模型，其主要流程如图1 所示。

图1 自适应Kriging 模型建立流程Fig.1 Process of constructing an adaptive Kriging model

ERF（Expected Risk Function）是一种自适应Kriging 常用的学习函数，其基本思想是基于预测值符号（正负）不确定性的思想，选择候选样本中符号预测风险最大的样本用于更新实验设计[18]，学习函数ERF 一般被定义为：

其中，sign (•)是符号函数，ERF 函数值最大样本点的符号被误判的风险最大，候选样本集中ERF值最大的样本被识别出来用于更新实验设计，并重新生成Kriging 模型。样本的ERF 值越小，样本符号被误判的概率就越低，文献[18]给出收敛条件建议值为

2 重要抽样法

重要抽样法通过采用重要抽样密度函数代替原来的抽样密度函数，使得样本落入失效域的概率增加，以此获得高的抽样效率和快的收敛速度[19-22]。其基本原理和公式为，通过引入重要抽样密度函数hx(x)，将求解失效概率的积分式转换为以hx(x)为密度函数的数学期望形式，即：

在开展重要抽样计算过程中，由于设计点是失效域内对失效概率贡献最大的点，重要抽样的中心一般选择为设计点。这样按照重要抽样密度函数抽取的样本点就有比较大的概率落在失效域内，从而提高了重要抽样法的计算效率，使其更快地收敛于真值。

本文结合自适应Kriging 和重要抽样法提出了一种用于求解失效条件为非随机变量的极小失效概率问题的重要抽样法，该方法仅适用于处理单失效模式的问题，且一般仅适用于失效条件为非随机变量的失效问题的求解，可用于计算较低载荷下耐压球壳的可靠性问题。该重要抽样法首先使用自适应Kriging 方法构建较高失效概率下的模型g1Kriging(x)，在此基础上，使用改进一次二阶矩法获得重要抽样方向，在重要抽样方向上仍然使用自适应Kriging 方法计算得到较低失效概率下的设计点MPP2，并以此设计点为中心，使用自适应Kriging 方法构建较低失效概率下的模型g2Kriging(x)，然后验证g2Kriging(x)对应的设计点MPP3距离g2Kriging(x)样本空间边界的距离。若MPP3所有变量距离样本空间的边界大于等于随机变量的3倍标准差，说明建立的Kriging 模型g2Kriging(x)能较好反映设计点附近的失效特征，可在g2Kriging(x)的基础上开展重要抽样计算；若小于3 倍的标准差，则重新以MPP3为中心建立Krging 模型，直至满足判断标准。计算流程如图2 所示。其中重要抽样方向为标准正态空间中从原点指向设计点的方向，该方向的物理意义是功能（失效）函数最速下降方向[23]。

图2 重要抽样法流程Fig.2 Process of importance sampling

3 数值算例

3.1 算例1

该算例来源于文献[24]，其本身是一个非线性程度较高的失效问题，包含2 个标准正态分布随机变量x1和x2，以其立方和不超过a建立约束，且x1和x2相互独立，x1和x2的均值为0.5，标准差为0.2。a取1 时，失效概率较高；a取4 时，失效概率较低，该问题的功能函数为：

算例1 失效边的界构建过程如图3 所示。在建立的高失效概率Kriging 模型的基础上，得到设计点MPP1，在均值指向MPP1的方向，通过自适应Kriging 方法计算得到低失效概率下的设计点MPP2，然后以MPP2为中心，建立低失效概率下的Kriging模型经验证后，为失效函数开展重要抽样，该算例的可靠性计算结果见表1。本文使用的重要抽样方法与蒙特卡洛法的计算结果接近，相差2.5%，但调用功能函数次数为39 次，其中建立高失效概率下Kriging 模型为18 次，计算低失效概率下设计点MPP2为6 次，计算低失效概率下kriging模型为15 次，调用功能函数次数远小于蒙特卡洛法。对于失效概率更低的情况，由于样本数一般需满足N=(102～104)/Pf的要求，直接采用蒙特卡洛法进行计算将是工程实际中无法接受的，而本文提出的重要抽样法可以方便地计算出失效概率。

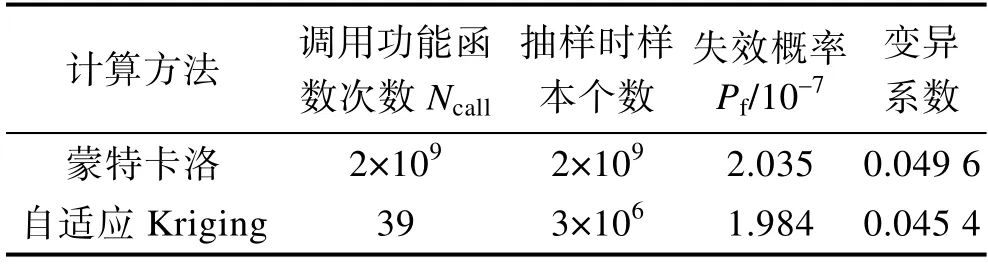
表1 算例1 计算结果Tab.1 Computed results of example 1

图3 算例1Kriging 模型构建过程Fig.3 Kriging model construction process of example 1

3.2 算例2

该算例来源于文献[23]，是一个包含3 个独立随机变量悬臂梁结构，其受到水平和竖直方向的载荷X和Y的作用（如图4 所示），以其自由端位移不超过D0为约束建立功能函数：

图4 悬臂梁结构Fig.4 Cantilever beam structure

式中：E、ω和t分别为材料的弹性模量、梁的宽度与厚度，ω=2.488 4m,t=3.888 4m、L=100m，E、X和Y为分布参数，见表2。0D取2.2 mm 时，失效概率较高；0D取2.8mm 时，失效概率较低。

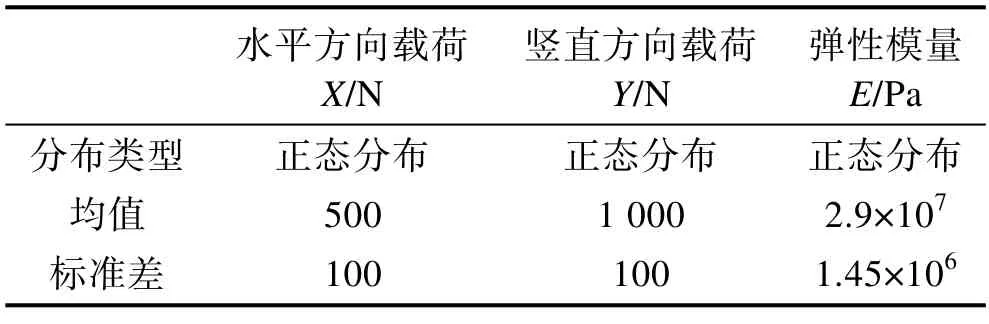
表2 算例2 模型参数Tab.2 Model parameters of example 2

该算例的可靠性计算结果见表3。本文使用的重要抽样方法与蒙特卡洛法的计算结果接近，相差1.4%，但调用功能函数次数为65 次。其中，建立高失效概率下Kriging 模型为31 次，计算低失效概率下设计点MPP2为3 次，计算低失效概率下Kriging 模型为31 次，调用功能函数次数远小于蒙特卡洛法。对于失效概率更低的情况，由于样本数一般需满足N=(102～ 104)/Pf的要求，直接采用蒙特卡洛法进行计算将是工程实际中无法接受的，而本文提出的重要抽样法可以方便地计算出失效概率。

表3 算例2 计算结果Tab.3 Computed results of example 2

4 耐压球壳可靠性分析

本文研究的耐压球壳的工作载荷为115 MPa，材料为钛合金，安全系数取为1.5，计算载荷为172.5 MPa。主要计算工作载荷和设计载荷下耐压球壳的可靠性指标，该结果可有助于评估结构的设计方案的安全可靠性以及为耐压球壳安全使用和结构优化提供支撑。耐压球壳的变量参数见表4。

表4 耐压球壳参数Tab.4 Parameters of pressure resistant spherical shell

首先使用自适应 Kriging 方法计算得到的172.5 MPa 下耐压球壳失效的Kriging 模型，样本空间范围为均值加减 5 倍的标准差，候选样本量为2×105个。在初始样本的基础上，采用ERF 学习函数的计算结果不断更新训练样本集。每个样本点均采用ABAQUS 有限元软件计算，参数化建模通过宏文件的方式完成，有限元模型如图5 所示。在球壳承载能力计算过程中，首先使用线性有限元获得结构的一阶屈曲模态，将一阶屈曲模态乘以球壳缺陷幅值作为球壳的初始缺陷，然后使用非线性有限元计算结构的承载能力[25]。文献[18]给出的收敛条件建议值是基于数值算例给出的，数值算例在候选样本点的响应值为该点响应值的精确解，而本文的响应值是通过有限元软件给出的，其本质上属于近似解，且计算过程需按照球壳尺寸重新生成有限元模型，网格等信息也随之改变。在这些因素的共同作用下，仍选择文献[18]给出的建议值将不再合适。经计算验证，在小于等于1×10–3后继续加入样本点，不会有明显降低，且结构的失效概率也未出现明显变化，因此收敛条件可取

图5 耐压球壳有限元模型Fig.5 Finite element model of pressure resistant spherical shell

在172.5 MPa 的载荷下，选择10 个样本点作为初始样本点，在学习函数的指导下，通过加入14 个样本点达到收敛指标，此时耐压球壳的失效概率为4.501×10–2，对应设计点MPP1。然后在重要方向上使用自适应Kriging 方法计算在115 MPa 下的设计点，选择2 个样本点作为初始样本点，在学习函数的指导下，通过加入2 个样本点达到收敛指标，得到设计点MPP2。以MPP2为中心，仍然使用自适应Kriging 方法建立115 MPa 下耐压球壳的Kriging 模型，选择10个样本点作为初始样本点，在学习函数的指导下，通过加入11 个样本点达到收敛指标，115 MPa 下建立的Kriging 模型的对应的设计点为MPP3。3 个设计点的数值见表5。计算可得MPP3设计点各个变量距离115 MPa 的Kriging 模型对应的样本空间边界均大于各个变量3 倍的标准差，说明最终建立的Kriging 模型能较好反映设计点附近的失效特征。因此，可以在此基础上开展可靠性计算，计算可得115 MPa 下耐压球壳的失效概率为4.094×10–96，失效概率变异系数为0.03。从115 MPa 下耐压球壳的可靠性计算结果看，115 MPa 的工作载荷下，耐压球壳的失效概率极低。