深海立管顺流与横流耦合涡激振动中的内流效应分析

赵桂欣, 孟 帅, 车驰东, 赵创业, 张文龙

(1.上海交通大学 海洋工程国家重点实验室,上海 200240; 2.江南造船(集团)有限责任公司,上海 201913)

当前海洋开发逐步进入深海区,深海区的特点是离岸远、水深深、地质条件复杂、环境恶劣且多变,因此确保作业安全是研发深海装备要解决的首要命题。涡激振动(vortex induced vibration, VIV)是立管疲劳失效的主要因素,严重影响立管寿命[1],实现涡激响应准确预报具有重要的工程意义。海洋立管的涡激振动已经得到广泛研究,但还有诸多问题需要进一步解决。例如,通过试验发现柔性立管在均匀流、振荡流等流型中展现不同涡激响应[2-4]。为解决计算流体力学(computational fluid dynamics, CFD)方法计算量大[5]、尾流振子模型的经验参数选择困难[6]等问题,Vandiver等[7-9]基于试验数据建立了时域半经验预报模型以实现快速精确预报柔性立管涡激响应。

自1950年观测到Trans-Arabian输流管由内流引起的强烈振动[10],内流效应开始受到学者们的广泛研究。Païdoussis[11]对内流效应进行了详细的阐述。深海立管系统由于长径比的大幅增加,柔性显著增强,内流效应开始凸显。同时在深海金属矿产资源开采时,管道内流密度大幅增大,内流效应必然进一步加强。学者们已经开展海洋立管涡激振动内流效应研究。研究发现,内流可影响涡激振动主导模态、振动轨迹和幅值等[12-14]。但当前大多研究局限于纯顺流向[15-16]或纯横流向[17-19]涡激振动。甚至还存在着相反的结论,例如,Dai等[20]发现在亚临界区海洋立管横流涡激振动响应幅值随着内流速度的增加而减小。Duan等[21]发现立管横流向涡激振动响应随内流速度的增加而增加。因此,深海立管涡激振动的内流效应亟待进一步研究。

1 仿真模型建立

1.1 深海立管顺流与横流耦合涡激振动方程

深海立管系统如图1所示。立管长度为L,水动力内径为Di,水动力外径为De,弯曲刚度为EI,单位长度质量为mp。立管内的单相流速度为Ui,且单位长度的质量为Mi。立管外海水密度为ρe。采用欧拉坐标oxyz, 原点o设在井口位置,z为重力反方向,x方向受到均匀洋流且流速为Ue,因此x方向为顺流向,y方向为横流向。

根据哈密顿原理

(1)

式中:T为系统动能;V为系统势能;δW为非有势力做的虚功。忽略内流增压效应和重力作用,得到立管的横流向(cross flow, CF)和顺流向(in line, IL)振动方程为

(2)

(3)

1.2 水动力模型

均匀洋流作用下采用的涡激振动水动力计算模型如图2所示。其中横流向流体力为

(a)

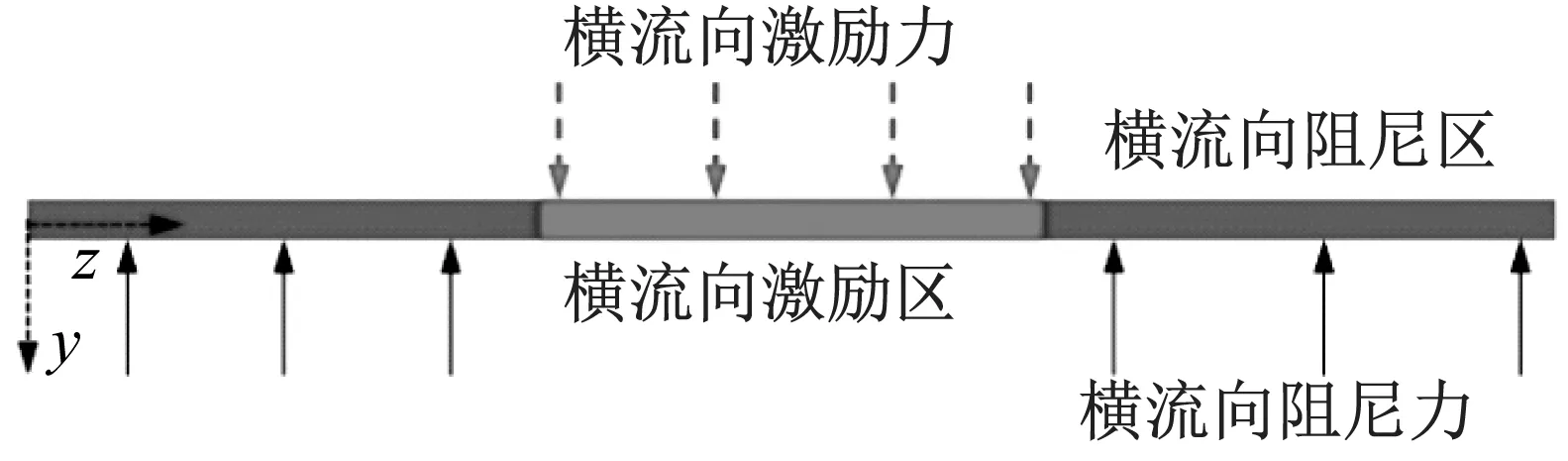
(b)图2 采用的水动力模型示意图Fig.2 The adopted hydrodynamic force model

FCF=Fma,CF+Fvor,CF

(4)

(5)

式中:ACF为横流向的振动幅值;a0,a1为基于试验得到的经验系数,a0=0.31,a1=0.89[22]。在激励区Fvor,CF=Fex,CF,Fvor,CF为横流向的涡激力,Fvor,CF的具体计算方法在1.2节中介绍。顺流向流体力为

FIL=Fma,IL+Fvor,IL+Fd,IL

(6)

(7)

式中,Cd为拖曳力系数。采用文献[23]中的阻尼系数模型

(8)

式中:Cd0为静止刚性圆柱的阻力系数,Cd0=1.2;Nd为横流向涡激振动主导模态的阶数;fex,CF为横流向涡激振动主导频率;yRMS为横流向位移响应均方根值。在顺流向激励区Fvor,IL=Fex,IL,Fex,IL具体计算方法在1.2节中介绍。

1.3 顺流向与横流向涡激力计算

首先定义修正的第j阶无量纲固有频率

(9)

图3 雷诺数与斯特劳哈尔数关系Fig.3 The relationship between Re and St*

(10)

(11)

不同阶数激励频率对应的激励区不能重叠,对于均匀来流作用下的均匀立管,根据文献[24]可定义基于能量考虑的激励系数以确定不同激励频率优先级

(12)

(a) 横流向

(b) 顺流向图4 采用的涡激振动激励模型参数Fig.4 The parameters in the CF/IL VIV excitation model

(13)

(14)

式中,Ce,CF,j、Ce,IL,j为第j阶主导激励频率的激励力系数可依据图5取得。P(0,Ce,A/De=0),Q(A/De,Ce,max,Ce,max)和R(A/De,Ce=0,0)可参考图4计算得到。φj,CF、φj,IL分别为横流向和顺流向激励力的初始相位角,取值与模态形状有关。以简支梁二阶固有模态为例,如图6所示。当模态值为正时φj=0,当模态值为负时φj=π。

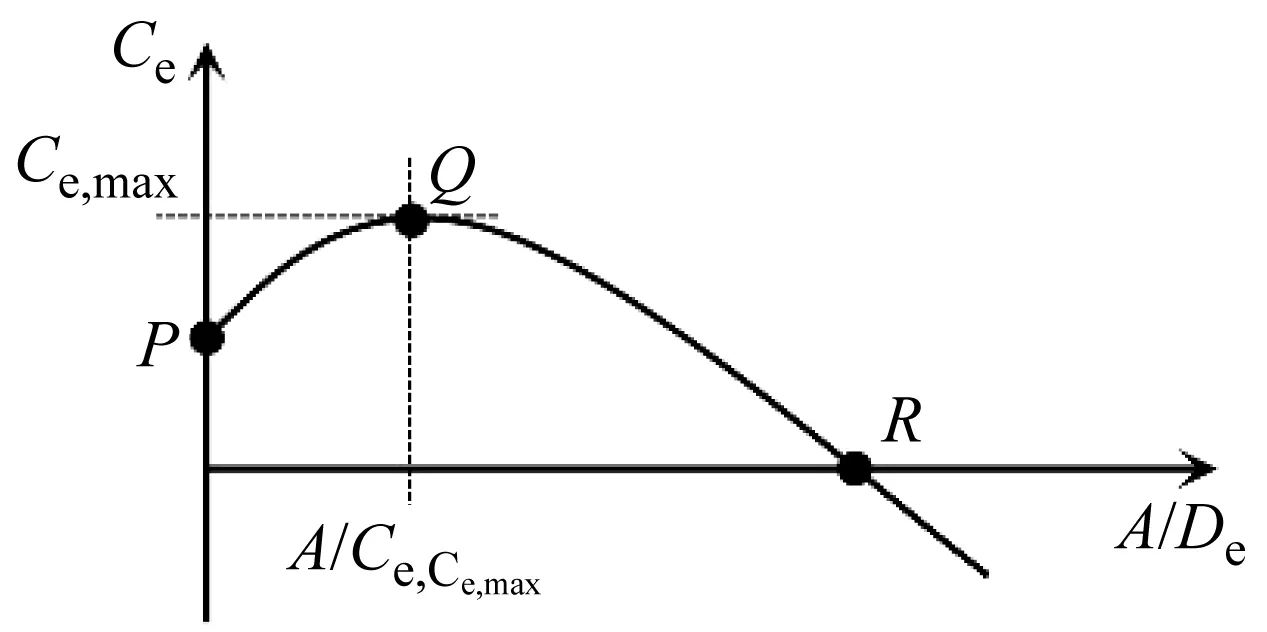
图5 Ce与A/De关系图Fig.5 Parabolic function of Ce vs A/De

图6 横流向/顺流向涡激激励力初始相位角Fig.6 The initial phases of the CF/IL VIV excitation forces

1.4 求解方法

采用有限元法对立管振动控制方程即式(2)和式(3)进行离散,然后使用Newmark-β法进行求解仿真。通过增加单元数和减小时间步长来保证计算结果收敛。

2 仿真模型验证

2.1 内流效应验证

采用空气中的柔性输流管系统进行内流效应验证。首先定义无量纲参数

(15)

式中,Ωj为输流管系统第j阶固有圆频率。之前的研究已经完成简支柔性输流管验证[25]。参考文献[11]中两端固定输流管参数:管道无量纲长度为1,cs=0,β=0.1。计算得到系统的前三阶固有频率ωj(j=1,2,3)随着ui的变化曲线如图7所示,与文献[11]结果吻合良好。

图7 输流管系统在不同ui下的前三阶固有频率ωj(j=1,2,3)Fig.7 The predicted ωj(j=1,2,3) of the pipe at different ui

2.2 立管顺流与横流耦合涡激振动验证

文献[26]中的立管模型参数如表1所示。对洋流速度Ue=1.6 m/s和Ue=2.8 m/s两种工况进行仿真,计算结果与文献拟合较好。这里以Ue=1.6 m/s为例,预测的顺流和横流耦合涡激振动位移均方根值如图8所示,仿真不仅捕捉到主导模态,而且位移响应预报也较好。位移响应计算结果与试验数据存在差异的原因可能是计算过程中使用的附加质量系数是定值,实际情况下附加质量系数随着外部流速和立管响应而发生变化[27]。

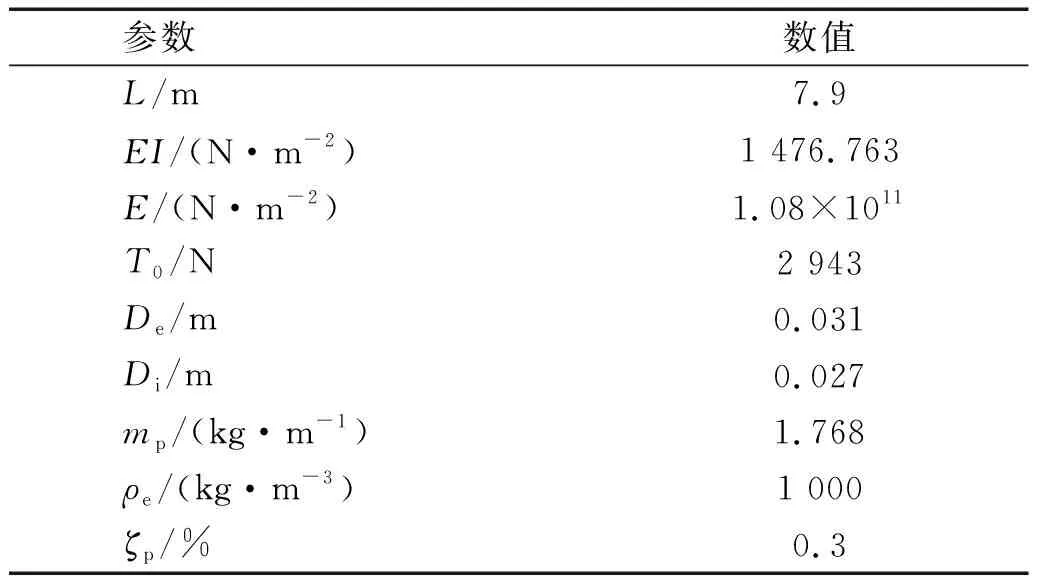
表1 柔性立管模型参数Tab.1 Parameters of a flexible riser

(a) 横流向

(b) 顺流向图8 预测的横流向和顺流向涡激振动位移均方根值Fig.8 The predicted RMS displacements of CF and IL VIVs

3 顺流与横流耦合涡激振动中的内流效应

采用表1立管模型,假设均匀来流速度Ue=0.8 m/s,1.2 m/s,1.6 m/s,2.2 m/s,内流密度设定ρi=1 000 kg/m3,1 500 kg/m3,2 000 kg/m3,2 500 kg/m3,先计算各工况立管系统固有频率得出临界流速,然后将内流速度从Ui=0以5 m/s 逐步增加至临界流速,以探究内流速度和密度对立管横流向/顺流向涡激耦合振动的影响。研究发现,在不同洋流速度Ue下的内流效应是一致的,这里仅以Ue=1.2 m/s为例进行阐述。

3.1 横流向涡激振动

图9 横流向涡激振动主导模态Fig.9 The dominant modes of CF VIV

图10 横流向涡激振动主导激励频率Fig.10 The dominant excitation frequencies of CF VIV

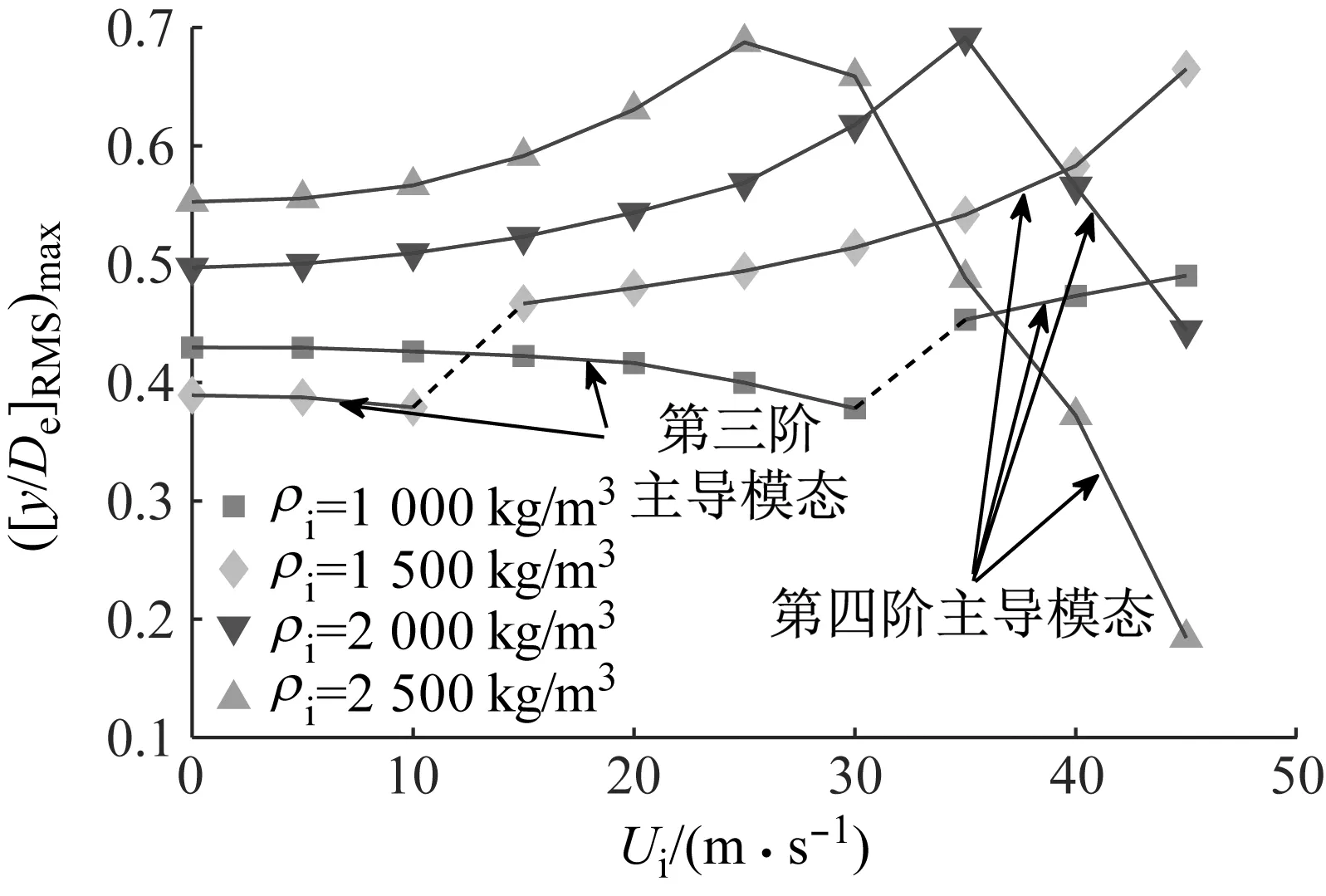
图11 横流向位移均方根的最大值Fig.11 The maximum RMS displacements of CF VIV

3.2 顺流向静态位移

图12 顺流向静态位移最大值Fig.12 The maximum static deformations in IL direction

3.3 顺流向涡激振动主导模态和主导频率

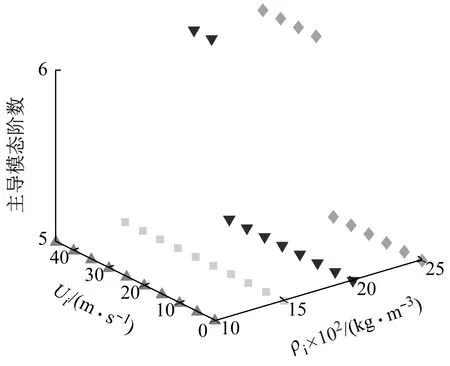
图13 顺流向涡激振动主导模态Fig.13 The dominant modes of IL VIV

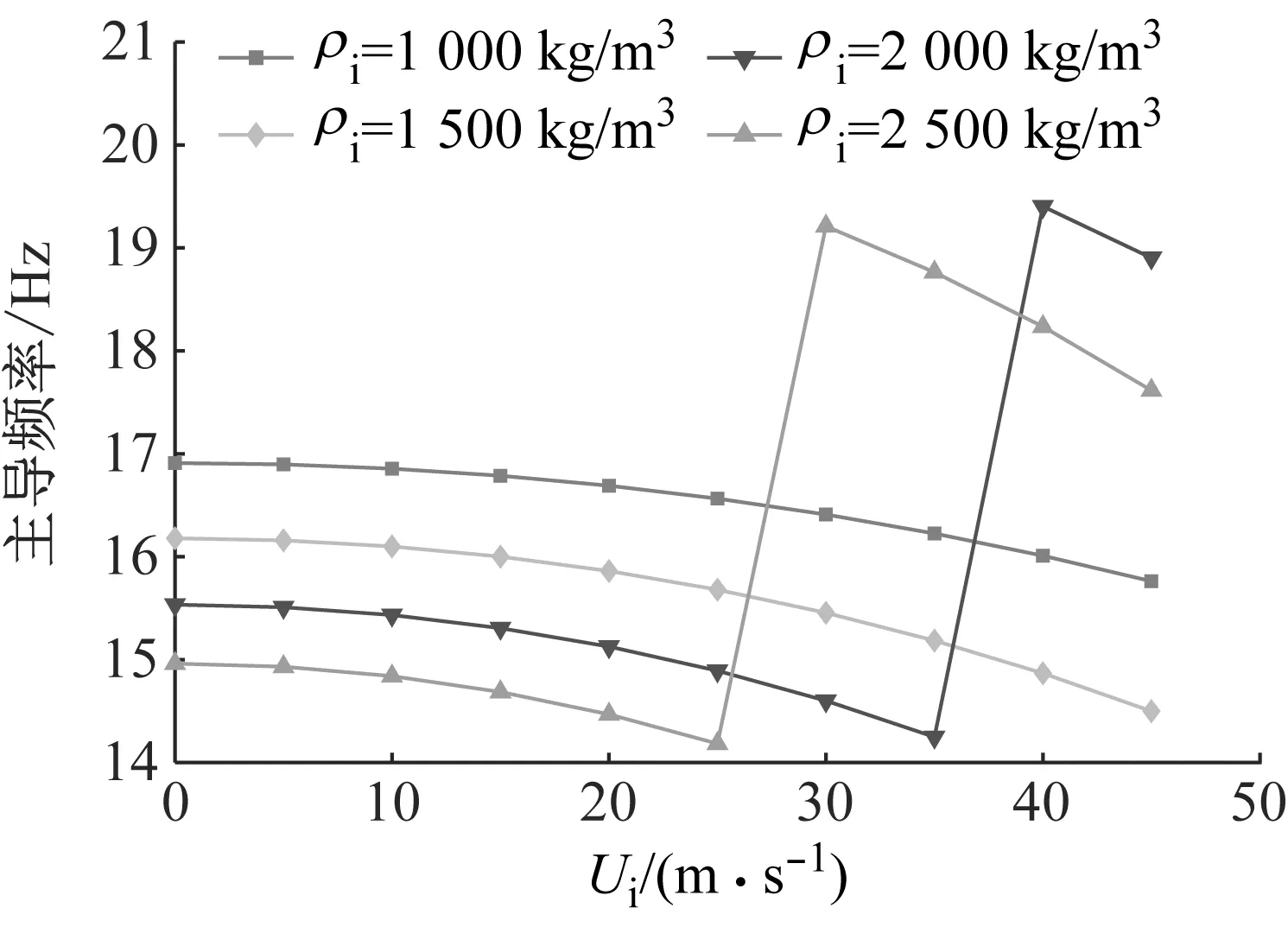
图14 顺流向涡激振动主导激励频率Fig.14 The dominant excitation frequencies of IL VIV

3.4 顺流向动态位移幅值

立管系统在不同Ui和ρi下的振动位移均方根的最大值([x/De]RMS)max如图15所示。需要特别指出的是,[x/De]RMS是顺流向动态响应减去静态形变求得。可以看出,内流效应对([x/De]RMS)max有不可忽略的影响,但由于([x/De]RMS)max是内流效应、顺流向的拖曳力(受到横流涡激响应的影响)和顺流向涡激效应联合作用的结果,很难区分出内流效应进行单独分析,因而不能通过顺流向主导频率和主导模态的变化来解释([x/De]RMS)max随内流速度的变化。

图15 顺流向位移均方根的最大值Fig.15 The maximum RMS displacements of IL VIV

4 结 论

基于哈密顿原理,采用半经验涡激振动水动力时域模型,建立了含内流深海立管顺流和横流耦合涡激振动仿真模型,采用有限元法进行仿真计算,分析了立管在不同均匀洋流速度下,内流速度和内流密度的变化对横流与顺流耦合涡激振动下的位移响应、主导模态和主导频率的影响。研究发现,当洋流速度和内流密度一定时:

(1) 由于内流离心力可降低立管系统的固有频率,随着内流速度的增加,顺流向和横流向涡激主导频率都将不断减少,一旦脱离激励区,主导模态将立即转移到高一阶模态,同时主导频率会发生阶跃性增加。

(2) 随着内流速度增加,立管横向位移均方根的最大值是增加还是减少取决于横向涡激主导频率是接近还是远离涡脱频率。

(3) 当横流向涡激振动主导模态不变时,由于内流离心力可降低系统刚度,顺流向的静态位移随着内流速度的增加而逐步增加。当横流向主导模态转移至高阶时,顺流向的拖曳力系数会发生突然减少,这将导致静态位移呈现阶跃性下降。

(4) 内流效应对顺流向振动响应有着不可忽略的影响。立管顺流向振动响应是内流效应、拖曳力(受到横流涡激响应影响)和顺流向涡激流体力联合作用的结果。

本研究可以为深海立管动力学响应预报提供参考,但其局限性主要包括:① 研究中设定洋流为均匀流,但是在实际工程中洋流形式将会更加复杂;② 为了区分内流效应和重力效应,研究中忽略了重力效应;③ 研究中设定内流为单相流,但立管在输运油气或矿浆等资源时内流为多相流;④ 研究中设定了附加质量系数为恒值Ca=1,但在实际涡激振动过程中立管的真实附加质量系数将随着外部流速和立管响应发生变化。这些问题需要在未来工作中开展进一步研究。