基于多尺度相位聚合轨迹表示的出行方式识别模型

张驰，顾益军

（中国人民公安大学 信息网络安全学院，北京 100038）

0 概述

出行方式识别是指从给定的轨迹数据模型中推断出用户的出行方式，如步行、跑步、骑行、自驾、乘坐公交车和乘坐出租车。通过对出行分布方式的推断，交通管理机构能够制定适当策略缓解市民出行压力、交通拥堵及空气污染。

近些年，机器学习方法被广泛应用于建立识别模型，并在出行方式识别方面起到了一定的作用，如K近邻（KNN）［1］、支持向量机（SVM）［2-3］、决策树（DT）［4］、随机森林（RF）［2，5］和神经网络（多层感知机网络［6-7］、卷积神经网络［8-10］、循环神经网络［11］等），其中支持向量机、神经网络和随机森林方法应用较为广泛。值得注意的是：一些研究利用随机森林方法实现有效的出行方式分类；另一些研究将其他方法与随机森林方法相结合进行性能评估［12-14］。文献［12-14］研究结果表明，在多数场景中，随机森林方法通常能够获得最好或次好的评估性能。詹益旺等［15］将BIRCH 算法改进为多阈值聚类算法（M-BIRCH），并与DBSCAN 相结合形成一种动态阈值聚类挖掘方法。李喆等［16］提出一种基于支持向量机的出行方式识别模型，利用粒子群算法优化支持向量机参数进行出行方式识别。但文献［15-16］机器学习方法使用特征工程学方法提取特征作为输入，通常需要一个复杂的特征提取过程，不适用于数据丰富的应用环境。

基于深度学习的轨迹挖掘方法往往能够在较大数据量的环境中取得更好的效果。FANG等［7］开发一种基于深度神经网络（DNN）的智能手机用户出行方式识别模型，模型输入轨迹被表示为固定大小的向量，DNN 模型的优势是可以自动从输入向量中学习重要的高维特征。另外，在许多出行方式预测方案中已经验证了卷积神经网络（Convolution Neural Network，CNN）擅长捕捉局部特征依赖关系［17-19］。DABIRI等［9］将每个轨迹表示为一个固定大小的矩阵，开发一个CNN 网络来学习局部特征和时空相关性。DABIRI等［8］提出一种半监督的卷积自动编码结构（SECA），根据GPS 轨迹并联合有监督和无监督两种方式来识别用户出行方式。郭茂祖等［20］将CNN 网络与GRU 网络相结合，在通过CNN 网络捕捉局部特征依赖关系的同时，利用GRU 网络捕捉长序列间的语义关联，从而更好地识别用户出行方式。YAZDIZADEH等［10］训练多个CNN 模型作为一组基础学习器，并优化所使用的每个基础学习器的参数，将平均投票数、投票总数等参数融入随机森林模型。实验结果表明，集成模型性能会优于单独的CNN 模型，并且随机森林模型可以更好地处理多种异构的模型结果。但是上述方法仅关注数据的局部属性而忽略轨迹数据中的全局信息，因此为了提取更精准的局部特征，要求GPS 数据具有较短的采样时间间隔和统一的采样率。

SOARES等［21］通过插入额外的传感器（加速度计、陀螺仪等）来提供更多属性特征，并探索了利用降维特征工程与基于自动机器学习（AutoML）的超参数优化方式，在降低成本的前提下提高识别精度，但这种插入额外传感器的工作方式限制了模型的实际使用范围。

在现实工作环境中提高GPS 采样率或者插入更多传感器会导致用户移动设备的能耗大幅提高，从而极大降低用户体验，并且在现实应用环境中难以对所有数据采集设备制定统一的参数，因此采样数据常常有着不同采样率，这也对目前已有的出行方式识别模型的准确率带来更多的干扰。为了降低出行方式识别工作对高采样率的依赖并降低由采样率的不同带来的干扰，本文提出基于多尺度相位聚合-深层神经决策森林（Multi-scale Phase Aggregationdeep Neural Decision Forests，MPA-NDF）的出行方式识别模型。通过特征提取层分别提取原始轨迹数据中的局部和全局特征生成令牌，利用卷积的方法提取时空信息。使用相位检测令牌混合（Phase-Aware Token Mixing，PATM）算法［22］从属性的高维特征中捕捉关键特征来发现轨迹中的潜在信息，利用令牌间的相位关系相互聚合获得令牌间的相关性，增加分类准确度。采用深层神经决策森林算法［23］作为最终分类器，提高分类结果的准确率。

1 相关定义

对于原始GPS 轨迹数据，为了获取其中有效信息，需要提取数据文件中的用户轨迹及其中的统计学特征。

定义1 用户轨迹是连续的GPS 点序列，即T={p1，p2，…，p|T|}（|T|表示用户轨迹的总长度），每个轨迹点具有纬度、经度和时间戳3 个属性，即pi=的每条轨迹都与一种出行方式相关。

定义2 轨迹段是轨迹T的子序列，将从i到j的轨迹段表示为Ti，j={pi，pi+1，…，pj}（i＜j），在之后的步骤中将划分用户轨迹为k个子段以得到子轨迹。

定义3设di，i+1表示为两个GPS 轨迹点pi和pi+1间的直线距离，设ti，i+1表示pi和pi+1间的时间差，因此计算pi和pi+1间的局部速度为vi，i+1=di，i+1/ti，i+1。同样地，在轨迹段Ti，j中的平均速度为vi，j=，相邻速度差为Δvi，i+1=vi+1-vi。

定义4 计算点pi和pi+1间的速度变化量为Δvi，i+1=vi+1-vi，计算轨迹中的 局部加速度特征表示为ai=Δvi，i+1/ti，i+1。

定义5 加速度变化率为两相邻点间的加速度变化量与时间差的比值，且两点间加速度的变化量为Δai，i+1=ai+1-ai，则加速度变化率表示为jpi=Δai，i+1/ti，i+1。

定义6设点pi到pj的方向为为同正北或正南方向的夹角，则方位角变化率Bpi可表示如下：

定义7 特征序列是使用特征工程学方法从用户轨迹或轨迹段中取其中相邻的2 个或3 个GPS 点（数量由属性计算方法决定）计算出属性特征，通过轨迹原有的时间顺序排列得到的序列表示为A={a1，a2，…，an}，其中，a表示属性特征标量。

定义8 通过计算特征序列中属性特征的期望值aavg、中位数amed、最大值amax等统计学指标，提取相应轨迹数据中的出行特征，所得统计学指标被称为出行特征值。

2 基于MPA-NDF 的出行方式识别模型

本文提出的基于MPA-NDF 的出行方式识别模型结构如图1 所示。首先，为了降低模型对采样率的依赖，使用一种多尺度特征提取方法，分别提取局部和全局属性的出行特征值组成出行特征向量（称为令牌）构成出行特征矩阵，所提取属性包括行驶速度、加速度、加速度变化率和方位角变化率等。局部出行特征矩阵中每个行向量包含了对应轨迹段中相应空间特征，同时各向量依照原有时间顺序排列，使得出行特征矩阵保留了轨迹原有的时空分布特点。然后，引入卷积神经网络学习出行特征矩阵中潜在的空间和时间特征，利用卷积神经网络学习感受野映射范围内数据相关性和高维特征的特点，合理调整感受野范围，使得到的出行特征矩阵的高维表示中每个元素都包含了对应向量的时空信息，以此达到提取属性出行特征矩阵中时空特征的目的。通过相位检测令牌混合层学习轨迹长序列间的相位关系。最后，将得到的轨迹表示送入深层神经决策森林层，确定用户出行方式。具体而言，模型共由3 个主要部分组成：1）特征提取层，包括局部特征提取和全局特征提取两部分，局部特征提取部分通过将轨迹划分为不同尺度的轨迹段，并提取每个尺度上的局部属性特征形成出行特征向量，全局特征提取部分针对整个用户轨迹提取全局属性出行特征值，形成全局出行特征向量，所构成的两种向量被视作令牌，通过卷积神经网络自动学习其中高维特征；2）相位检测令牌混合层，通过将CNN 提取的高维特征引入相位检测令牌混合层进行相位特征检测与聚合，从而检测不同出行方式的长序列异质性特征；3）深层神经决策森林层，以相位检测令牌混合层的降维表示作为输入，由包含一组深度神经决策树的神经决策森林组成，准确识别出行方式。

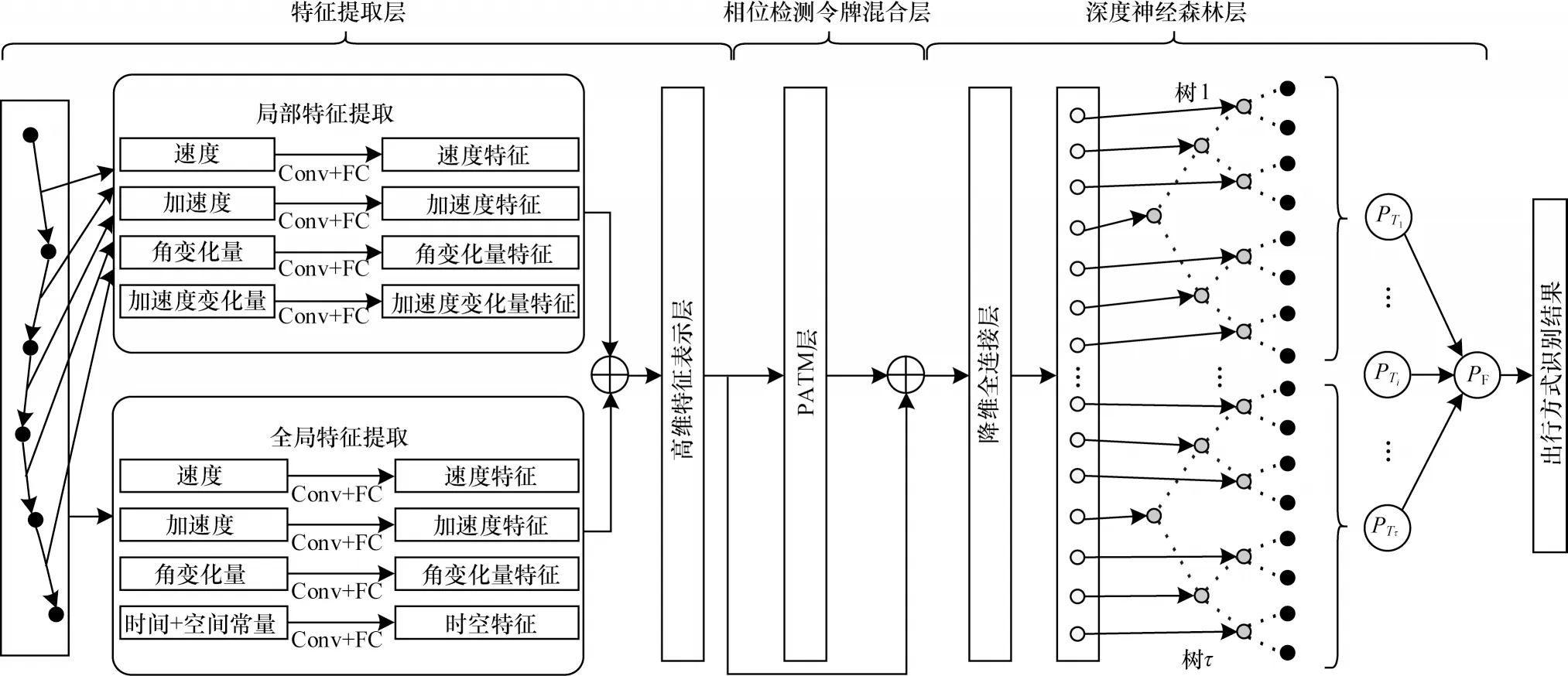
图1 基于MPA-NDF 的出行方式识别模型结构Fig.1 Structure of travel mode identification model based on MPA-NDF

2.1 轨迹特征提取层

局部和全局特征提取层如图2 所示。为了提取轨迹中隐藏的有效特征，采用卷积神经网络和全连接层组成的神经网络结构作为特征提取层的主要结构。首先构建局部和全局出行特征向量，然后使用卷积和全连接层提取它们的隐藏特征。

图2 局部和全局特征提取层结构Fig.2 Structure of local and global feature extraction layers

2.1.1 局部特征提取层

局部特征提取层的输入数据是用户轨迹T=｛p1，p2，…，p|T|｝，从用户轨迹中获得对应出行特征向量，即速度、加速度、加速度变化率、方位角变化率4种属性的出行特征向量。首先，将用户轨迹T=｛p1，p2，…，pi，…，p|T|｝（0 ＜i≤|T|）平均划分成不同粒度的k个等长轨迹段（k=4，6，8），每个子段中分别计算相邻两个点间的局部属性，在用户轨迹中每个子轨迹段的局部特征序列被表示为（0 ≤m＜k），其中，a表示一种属性的出行特征值，m表示在k个轨迹段中的第m个子段。然后，计算局部特征序列中相邻两项之差得到，并求中每个出行特征值的绝对值得到分别满足最后，针对每个分别提取这3 种特征序列中的平均值、中位数和最大值共9 个元素，依次填充到第m个子段所对应的9 维出行特征行向量中。总体而言，局部出行特征向量从对应属性的局部特征序列中提取出行特征值构成，局部特征序列由被切分成的不同粒度的轨迹段计算得到。将由同一个轨迹段对应的出行特征向量按原有顺序排列形成用户轨迹局部出行特征矩阵，表示为出行特 征矩阵xk∈Rk×9可以表示子轨迹段中的局部特征信息的二维分布矩阵，其中每个行向量被称为一个令牌。令牌由卷积和全连接操作提取其中高维时空特征。

在局部特征中，不同分段有着不同程度的重要性，分段之间的差异性和出行特征向量在时间维度上的分布特点是出行方式识别的一种高维特征。例如，自驾和乘坐公交车这两种出行方式虽然在速度、加速度等表象特征上具有较高的一致性，使得两种出行方式不容易区分，但对整个轨迹而言，由于包含公交车和地铁在内的公共交通需要在车站停靠，会产生大量周期性的停留点，而其他出行方式的速度等特征分布会更加平稳，使得区分这些出行方式成为可能。利用卷积神经网络和全连接层自动学习时空高维特征，设置卷积核尺寸包含相邻行向量，即有，其中，*表示卷积 操作，s表示第s个卷积核和分别表示卷积神经网络的卷积核参数和偏置，且有（α表示卷积核的大小，取α=2），非线性激活单元ReLU 用作激活函数为卷积层加入非线性运算单元。不同卷积核产生的列向量被连接产生最终输出，其输出结果为，其中，c表示卷积核的总数。输出结果将被送入一个包含60 个神经元的全连接层中，以提取更高纬度的信息并调整输出形状。该层最终得到局部特征提取结果，表示为

通过上述特征提取过程，分别提取4 种属性的局部出行特征矩阵，最终输出结果是一个包含4 种属性的局部出行特征矩阵，其中，SP、ACC、JK 和BR 分别表示速度、加速度、加速度变化率和方位角变化率4 种属性。

2.1.2 全局特征提取层

由于仅依靠局部特征不能很好地识别不同出行方式在宏观上的差异性，因此需要通过从样本中抽取全局属性特征来表达这种宏观特征。所提取属性包括速度、加速度、方位角变化率和全局时空特征。

在提取全局速度特征前，首先需要计算的是GPS 点之间的平均局部属性值ai，i+1(0 ＜i≤|T|-1)，由此得到整个轨迹序列的特征序列。全局出行特征向量是从已计算完成的特征序列中抽取9 个出行特征值构建而成，即xD∈R1×9，其中，下标D 表示全局出行特征向量的属性，即D ∈{SP，ACC，BR，ST}，ST 表示轨迹全局时空特征。每个向量同样称为一个令牌。该向量包含9 个元素，每个元素分别代表一个出行特征值，其中前4 个元素分别为整个轨迹局部属性的平均值aavg、中位数amed、最大值amax和整个序列的标准差astd，后5 个元素计算需要首先将序列按照从大到小顺序排列，表示为AD={a1，a2，…，a|T|-1}，再分别将长度乘以预设百分数值（取10%、25%、50%、75%和90%），向下取整得到出行特征向量中元素在整个轨迹序列中的索引，表示为a10%、a25%、a50%、a75%和a90%。以a10%为例，在特征序列AD中的索引可表示为其中表示向下取整。最终得到的全局出行特征向量表示为xD={aavg，amed，amax，astd，a10%，a25%，a50%，a75%，a90%}。

按照上述描述计算得到速度、加速度和方位角变化率3 种出行特征向量。值得注意的是，由于本文研究的是在GPS 采样率较为稀疏情况下得到的轨迹数据，此时全局加速度变化率属性并没有较好的区分度，因此在全局特征序列提取过程中，没有加速度变化率的特征提取过程，取而代之的是提取当前轨迹的全局时空特征得到的全局出行特征向量。全局时空出行特征向量包括轨迹的总路程、轨迹全程经历的总时间、轨迹起始时间点（不含日期，精确到h）和出行当天星期几4 种全局时空特征。

全局特征提取的高维特征提取方式与局部特征提取相似，将提取的令牌送入卷积神经网络得到并同样将所得向量送入全连接层，得到高维特征表示为因此，全部属性的出行特征向量被提取后，最终得到全局特征提取层输出为

2.1.3 属性高维特征提取

把多轴系统简化成单轴系，把阻转转矩Mf折算至变频电动机轴上为Mr，此时把Mr看作等效的阻转转矩。将计算轴作为计算基准点，以确保系统的功率传输关系和机械总动能一定为折算原则，将系统转动惯量化为两部分：变频电机端转动惯量的和标记为JⅠ；靠低速轴侧的转动惯量之和记作JⅡ[4]，如图2(b)所示。

在出行方式识别工作中，学习不同的属性间的关系可以给出行方式分类工作提供更高的准确率。例如，在汽车行驶过程中，在有较多转弯路段行驶时方位角变化率增大的同时常伴随减速过程，而步行等出行方式不会有明显减速，这可以有效区分多种不同的出行方式，因此通过引入高维特征提取层来获取这种特征。如图3 所示，输入数据被表示为xL，G=xL⊕xG。

图3 属性高维特征提取层结构Fig.3 Structure of attribute high-dimensional feature extraction layer

考虑到提取输入数据高维特征的需要，首先将卷积神经网络特征映射至高维空间，即有其中l表示第l个卷积核。采用的高维特征提取由两层卷积神经网络层组成，每层卷积核表示为，其中c为本层输入数据的通道数，两层卷积神经网络的卷积核数量分别为β和β×2。卷积神经网络输出结果最终表示为xL，G，Conv。在每层卷积神经网络操作后，将结果送入一个自适应平均池化函数以完成高维特征的下采样，并调整输出矩阵的维度。最终得到的高维特征提取层输出矩阵可以被认为是一个包含相位信息的令牌组成的轨迹表示矩阵。因此，需要使用相位检测令牌混合算法通过学习其中的信息来获得令牌间的相位关系。

2.2 相位检测令牌混合层

对于轨迹数据而言，卷积神经网络只能学习相邻令牌间的短序列特征关系，但令牌间的长序列相关性同样是影响出行方式分类结果的重要因素。为了动态调整神经网络中令牌与固定权重的关系，获得令牌间的相位关系，更好地捕获轨迹的长序列间的相关性特征，引入相位感知令牌混合层。如图4所示，该结构的输入为经过上一层的卷积神经网络编码后得到的输出xL，G，Conv（β×2 表示其编码后的通道数）。将每个输入的令牌视为一个既有振幅又有相位的波，用以动态调整识别模型中令牌与固定权重间的关系，更好地聚合令牌。

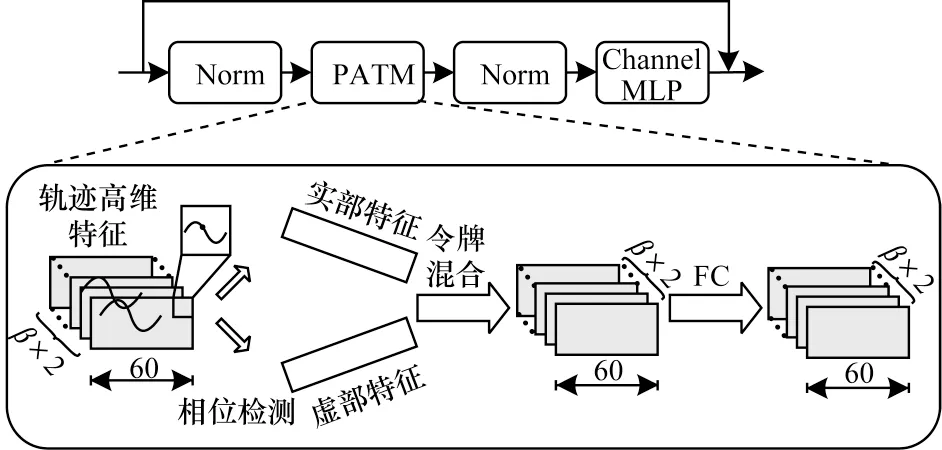
图4 相位检测令牌混合层结构Fig.4 Structure of phase-aware token mixing layer

在之前模块中提取的令牌可表示为具有振幅和相位的信息波：

其中：i 表示为满足i2=-1 的虚部；|·|表示绝对值运算；⊙表示哈达玛积；|xj|表示令牌振幅，是令牌内容的实值特征；eiθj是一个周期函数，元素总是具有单位范数，θj表示相位，是令牌在周期内的当前位置。利用振幅和相位得到每个令牌在复数域中的投影。

当不同令牌叠加时相位θj将调整它们的叠加模式。设表示波函数表示的令牌叠加结果，则其振幅|xr|和相位θr可以表示如下：

在式（5）中定义了复数域中的波状令牌表示，为了将其嵌入神经网络体系中，该波状令牌将欧拉公式展开，其结果以实部和虚部的形式表示，具体如下：

在上述函数中，波表示令牌被视为两个实值向量，分别表示实数部分和虚数部分，不同的令牌通过全连接层相互叠加形成新的令牌表示，具体如下：

其中：Wt和Wi都是可学习的参数。在式（10）中相位θk可以根据输入的数据的语义动态调整，因此θk同样设置为可学习的参数，以便于通过数据动态调整波状令牌的相位检测过程。

综上，在出行方式检测过程中引入一个相位感知令牌混合模块来执行上述过程，由给定令牌送入卷积层得到输出而来的轨迹表示矩阵，训练通道全连接层和相位检测模块生成振幅|xj|和相位θj，由波状令牌以式（8）的方式展开并最终由式（10）相互叠加聚合生成输出。通过将送入另外一个通道全连接层以增强表达能力，从而获得最终的输出。

2.3 深层神经决策森林层

为了尽可能有效地利用已经提取的高维轨迹表示矩阵，采用一种包含多个相互堆叠的神经决策树的深层神经决策森林层作为分类器。为了降低计算成本、提升效率及排除冗余信息，在样本被送入深层神经决策森林层前需要做降维处理。

将特征提取层的输出和相位检测令牌混合层输出相连接得到本层输入。由于当前输入矩阵中的每个元素都包含其对应令牌的聚合信息，因此使用一个4 层的卷积神经网络结构作为降维层，并且每2 层卷积层后加入一个自适应平均池化函数得到样本下采样输出。前2 层卷积核大小为16×1，卷积核数量分别为β和β/2；后2 层卷积核大小分别为2×1 和1×1，卷积核数量为β/4 和1。4 层卷积神经网络结构均采用ReLU 函数作为激活函数。

决策树由决策节点（或分裂节点，表示为N）和预测节点（或叶子节点，表示为L）组成。每个预测节点l∈L都持有一个概率分布πl。每个决策节点n∈N都持有一个由参数Θ决定路由策略的决策函数dn(x；Θ)：X→[0，1]。在随机路由的情况下，叶子节点的预测结果为到达叶子节点的期望值。因此，对于样本x而言，树T基于参数Θ的预测结果如下：

其中：π=(πl)l∈L并且πl表示样本到达叶子节点l并被分类为y的概率；μl(x|Θ)表示样本x到达叶子节点l的概率路由函数分别表示决策树节点中的两条分叉路径；1p是以自变量p为条件的指示符函数。

决策树以随机方式选择从内部节点到叶子节点以确保模型的可微性，随机路径的路由函数dn(x；Θ)定义如下：

其中：fn(x；Θ)是一个由样本x的参数Θ决定的实值函数，通过嵌入函数fn来赋予深度森林特征学习能力。

综上，由森林F={T1，T2，…，Tτ}（τ表示森林中树的总数）输出的分类结果最终概率分布是其构成的平均概率分布，可表示如下：

决策树对可学习参数Θ（叶子节点层之前的路径的影响参数）和π（叶子节点的预测概率）的估计需要通过反向传播算法求得。对于给定的数据集Γ而言，其整体最终损失函数可表示如下：

其中：L(Θ，π；x，y)表示训练样本对标签的损失函数。

3 实验与结果分析

3.1 实验设置

3.1.1 环境设置

实验运行环境为GPU NVIDIA Tesla V100-SXM2-32 GB，操作系统为Windows 10 64位，开发环境为PyTorch 3.8。实验数据采用GeoLife 轨迹数据集［8，24］。

3.1.2 数据处理

仅考虑步行、骑行、乘坐公交车、自驾、乘坐轨道交通5 种出行方式。规定了轨迹内两点间最大时间间隔，如果两个连续的GPS 点之间的时间间隔超过预先设定的阈值M，则划分用户的GPS 轨迹为多个子段。每段GPS 序列仅包含一个交通标签，因此轨迹将在出行方式转换处断开。GeoLife 轨迹数据集所包含信息如表1 所示。

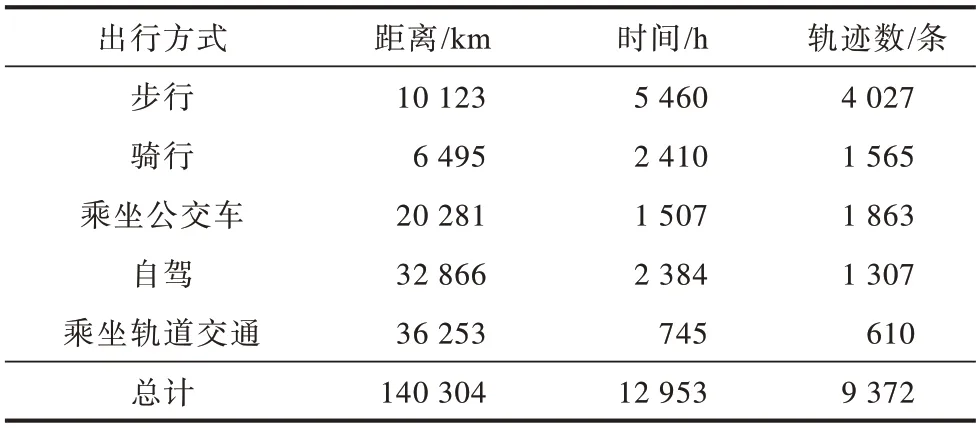
表1 GeoLife 轨迹数据集信息Table 1 Information of GeoLife trajectory dataset

受数据采集设备的影响，GeoLife 数据集样本中存在较多由噪声、误差等原因产生的错误值、离群点。为了尽可能删除错误样本的影响，设定以下过滤规则：1）删除轨迹序列中时间戳大于其后一个轨迹点的样本；2）设置每种出行方式的速度和加速度上限，如表2 所示。计算样本中每个轨迹点与前一个轨迹点间的平均速度，并删除超出速度上限的轨迹点。

表2 每种出行方式的速度和加速度上限Table 2 Upper limits of speed and acceleration for each travel mode

为了去除GeoLife 数据集样本中所存在的噪声干扰，引入Savitzky-Golay 滤波器［25］处理经规则过滤后的轨迹数据。Savitzky-Golay 滤波器是一种低通滤波器，其主要思想是使每个样本点在以该点为中心的奇数大小的窗口内用高次多项式进行最小二乘拟合，从而得到更加平滑的用户轨迹。

由于在GeoLife 数据集中，轨迹的GPS 采样率较高，其中多数采样时间间隔约为1 s，为了探索模型在低频采样率数据上的性能，对每个轨迹重新采样，使得连续点间的时间间隔至少为rs，并在低频重采样数据集上完成对比实验。

3.1.3 模型参数设置

将高维特征提取层中定义的卷积核数量β和决策森林中树的数量和树的高度设置为超参数，用于探索模型最佳结构。将轨迹片段切分为至多200 个轨迹点的轨迹段，并分别提取局部和全局特征送入不同超参数的模型中，确定模型的最佳结构。为了探索最佳的模型结构，使用原始高频采样数据集作为实验样本，而低频混合重采样数据集会在与基线模型的对比实验中使用，以对比不同模型在不同采样率状况下的表现。

对于高维特征提取层从浅层网络开始，逐渐增加层数，选择最佳的高维特征提取层结构，其中卷积核设置为1×3，激活函数设置为ReLU 函数，池化层设置为自适应平均池化函数，以保持其输出结果和输入每个通道的样本尺寸相同。将NDF 层森林中树的数量和高度设置为80 和10。测试不同β值对高维特征提取结构的影响，如表3 所示。

表3 不同β 值对高维特征提取结构的影响Table 3 Influence of different β values on the structure of high-dimensional feature extraction

同样地，对于NDF 层需要确定决策森林中树的最佳数量和每棵树的最佳高度。在测试过程中设置β=32，结果如表4 所示。

表4 不同β 值对NDF 结构的影响Table 4 Influence of different β values on the structure of NDF

综上可知，所提模型的最佳网络结构为：在CNN 层中β=32，即CNN 层由32 个卷积核和64 个卷积核的2 个网络结构组成，NDF 层由高度为10 的80 颗树组成。

3.2 结果分析

为了模拟现实情况下不同设备具有不同采样率的状况，与探索MPA-NDF 最佳网络结构所使用的训练集不同，使用3 种低频重采样数据。数据集分别划分为训练集和测试集，划分比例分别为8∶2，并把划分后的训练集混合打乱重组后形成新的训练集，训练后的模型将在不同的低频重采样数据集中测试得到结果。低频重采样时间间隔r分别设置为10、20、30 s，分别表示重采样后的轨迹点间隔时间不低于10、20 和30 s 的3 种不同的测试集。

基线模型将采用出行方式检测文献中广泛使用的机器学习和深度学习模型，包括K 近邻、支持向量机、决策树、多层感知机、随机森林、CNN［8］模型。以往文献中最优的手动提取特征方法［4，26］被应用于K 近邻、支持向量机、决策树、多层感知机机器学习模型，提取的特征包括GPS 段的总距离、平均速度、速度期望值、速度变化量、轨迹中前3 个速度、前3 个加速度、方位角变化率、出行方式停靠率和速度变化率。在随机森林、CNN 深度学习模型中，同样使用在所提模型中的速度、加速度、加速度变化率、方位角变化率5 种特征属性作为输入，以便模型自动提取对应高维特征。为了防止模型过拟合，当训练集和测试集误差达到5%则停止训练，并使用已得到的表现最好的权重参数作为模型参数进行对比实验。通过将所提模型获得的预测准确率与上述基线模型进行比较来评估总体性能，结果如表5 所示。

表5 不同出行方式识别模型对比Table 5 Comparison of different travel mode identification model %

由表5 可知，由于不同采样率的干扰，因此基线模型在不同采样率的数据集上的识别准确率表现出不同程度的扰动，具体表现为在低频重采样数据集的较高采样率的样本（r=10 s）上的识别准确率大幅度下降。所提模型在所有低频重采样数据上均具有最好的表现，相比于传统机器学习模型具有更好的抗干扰能力和更高的识别准确度，并且识别结果优于传统人工提取特征学习和单一深度神经网络模型。

4 结束语

本文提出一种基于MPA-NDF 的出行方式检测模型。通过预设规则切分用户轨迹得到轨迹段，使用特征工程学方法提取轨迹段中属性特征，并从属性特征中获得局部和全局出行特征向量（即令牌），通过将令牌按照用户轨迹原有时间顺序排列得到出行特征矩阵。引入卷积神经网络结构和PATM 层分别提取行特征矩阵中的时空特征与相位特征，完成对用户轨迹的多尺度相位聚合轨迹表示。最终使用NDF 层作为分类器，得到相应的出行方式识别结果。实验结果表明，所提模型相较于基线模型在低频重采样数据集上表现更加出色。后续将利用更多类型的位置数据（如手机信令数据），完成出行方式检测工作，并解决更多用户的出行方式识别问题，进一步扩展模型适用场景。