复杂低空无人机飞行冲突网络建模与精细管理

2023-10-17谢华苏方正尹嘉男韩斯特张新珏

航空学报 2023年18期

谢华，苏方正，尹嘉男，*，韩斯特，张新珏

1.南京航空航天大学通用航空与飞行学院，南京 210016

2.南京航空航天大学民航学院，南京 210016

随着国家低空空域管理改革的不断推进，民用无人机飞行需求呈现迅猛增长趋势，作为低空空域系统内的新兴用户，无人机目前已在商业、公共、军事、旅游、体育和防疫等领域得到广泛应用［1］。例如，在新冠肺炎疫情期间，无人机常被用于执行疫苗运输、物资配送、安全巡逻等各类任务［2］。2021年，中共中央、国务院在《国家综合立体交通网规划纲要》中首次提出要大力发展以低空空域为依托、以无人机和通航产业为主导的“低空经济”，这为无人机在智慧城市中的规模化应用带来了前所未有的发展机遇。

未来，无人机将在管制空域和监视、报告等非管制空域获得更大的自由活动权，而其高灵活和高机动特性［3］将随之带来一系列安全问题，并成为国内外航空界的关注焦点。尤其是在无人机逐步融入整个国家空域系统的趋势下，其运行安全水平还将影响公共运输航空、军事航空等传统空域用户。因此，研究复杂低空无人机飞行冲突网络建模与精细管理问题，成为当前及未来相当长一段时期内国际空管领域的研究热点和难点。

国内外在空域运行冲突管理领域已取得一系列研究成果，相关学者围绕冲突探测与解脱提出了诸多模型和算法。例如，Weinert等［4］针对低空作业场景，提出了一种基于空中碰撞风险的冲突管理方法，并对低空安全风险阈值进行了定义与度量；Mullins等［5］考虑入侵无人机的速度和性能，采用时间阈值代替空间距离阈值，提出了动态分离阈值的无人机冲突探测避碰模型。目前，使用最为广泛的航空器冲突探测方法大多基于几何计算，即通过每架航空器的飞行计划所需空域进行交叉判定是否有存在冲突［6-7］，该方法虽可准确计算无人机飞行计划冲突以及航迹冲突点，但是对于大规模的空域冲突检测效率较低。

为此，空域栅格化为无人机冲突检测提供了一种新的视角，该方法通过对空域进行栅格化处理，将其离散分解成一系列栅格单元，以此构建空域数据结构，进而可通过查询数据库表的方式进行冲突探测。Pongsakornsathien等［8］采用空域离散化方法，提出了一种新型的无人机系统交通管理（Unmanned Aircraft System Traffic Management， UTM）空域模型，实现了低空空域资源的动态管理。Zhai等［9］构建了基于空域栅格的空间数据库，建立了无人机碰撞检测模型。顾俊伟［10］提出基于4D网格的飞行冲突初筛算法，对多航空器间的飞行冲突进行探测。谢华等［11］提出了基于改进速度障碍法的无人机飞行冲突探测方法，设计了无人机飞行冲突解脱策略及其适用条件，构建了以最小化冲突解脱时间成本为导向的无人机飞行冲突解脱策略最优配置规则及实施流程。付其喜等［12］基于数学优化理论，提出了多机冲突解脱的双层优化算法。Virágh等［13］通过设定安全间隔，基于几何方法对二维和三维空间内交通密集场景下的飞行冲突进行研究。Innocenti等［14］引入了一种基于概率函数域的空中交通管制无冲突航迹生成方法，并开展了不同初始条件下的仿真。Alonso-Ayuso等［15］针对不同场景下的无人机运行情况建立非线性混合整数规划模型，判断无人机在特定约束条件下是否会发生冲突。Tang等［16］基于经典蚁群算法，提出了一种基于速度调整策略和航向调整策略的多无人机冲突解脱方法，提高了计算效率。Cecen等［17］采用两阶段优化方法，建立了自由航路空域航空器冲突解脱模型，并应用元启发式算法进行了求解。Pang等［18］提出了多机冲突解脱的双层优化自适应决策框架，改进了一种新的元启发式随机分形搜索算法，显著优化了航空器的四维航迹。张宏宏等［19］将“核仁解”的概念应用于冲突解脱领域，提出了基于优先级与公平性的冲突解脱算法。管祥民和吕人力［20］采用满意博弈论方法，研究了基于改变航向角策略的多无人机冲突解脱问题，通过解脱顺序优化实现了全局冲突解脱。

然而，当前研究仍存在以下不足：① 无人机冲突分析主要聚焦特定场景中的无人机个体冲突特征，未充分考虑全局层面无人机群体冲突网络的动态构建及其演化特性；② 无人机冲突探测主要基于预先设定的粗放式低空空域单元，未对无人机空间运行环境进行多层级分解建模，不能有效满足无人机飞行冲突的精细探测需求；③ 无人机冲突解脱主要聚焦统一规则下的两机或多机冲突场景，未充分考虑无人机个体调配优先级的差异对无人机群体层面的间接性波及影响。

本文针对多元化空域、高密度流量和高动态演化交织形成的复杂低空系统，通过构建基于冲突连边动态识别的无人机飞行冲突网络模型及特征参数，提出基于数字栅格的无人机飞行冲突精细探测算法，建立考虑优先级的无人机飞行冲突最优解脱方法，旨在实现低空无人机飞行冲突的精细化管理，为低空空域安全管理与无人机运行风险防控提供理论支撑和方法指导。

1 无人机飞行冲突网络建模及特征分析

本节采用GJK算法，构建了基于冲突连边动态识别的无人机飞行冲突网络模型，以平均冲突数量、平均运行风险和平均聚集系数等指标表征无人机飞行冲突网络特征，分析了无人机飞行冲突的动态演化特征。

1.1 模型构建

1.1.1 GJK算法框架及流程

GJK算法［21］是一种计算凸体之间距离的迭代方法，该方法通过向量映射构成闵可夫斯基差集（Minkowski Difference）。每架无人机可表示为一个立方体，满足GJK算法中的凸体计算。GJK算法计算2个立方体之间的距离，无人机A和无人机B之间的距离可表示为立方体A和立方体B之间的距离d(A，B)，定义为

式中：x和y分别表示立方体A和立方体B中的点；立方体A和B之间距离最近的2个点a∈A和b∈B满足‖ ‖a-b=d(A，B)。

在此基础上，进一步引入2个相关概念。

1）闵可夫斯基差集

闵可夫斯基差集是立方体A的所有点和立方体B的所有点的差值构成的点集合，可表示为

2个立方体的闵可夫斯基差集所构成的凸包称为配置空间障碍（Configuration Space Obstacle，CSO）。立方体A和B之间的距离可用闵可夫斯基差集表示为

则2个立方体之间的碰撞检测可使用闵可夫斯基差判断：当且仅当2个立方体的闵可夫斯基差集Mk(A，B)包含原点时，无人机A和B发生碰撞。

通过上述变化，可将立方体A和B之间的距离转化为两者的闵可夫斯基差与原点的距离，如图1所示，通过判断差集是否包含原点来确定2个无人机是否发生碰撞。

图1 闵可夫斯基差集距离转换示意图Fig.1 Schematic of Minkowski difference set conversion

将3个相同类型的无人机A、B、C表示为3个相同大小的立方体A、B和C，如图2所示，A和B接触，C和A、B远离，将算法迭代次数设置A、B和C为5 000次，因此得到的闵可夫斯基差集中包含5 000个点，将这些元素点置于坐标中显示，A与B、A与C的闵可夫斯基差结果如图3所示。

图2 无人机的立方体表达Fig.2 Cube representation of UAVs

图3 闵可夫斯基差集结果Fig.3 Result of Minkowski difference set

图3直观展示出了闵可夫斯基差集与原点的关系，如图3（a）所示，原点位于立方体A与B生成的闵可夫斯基差集内部，为了直观表现同时给出了二维侧视图，原点位于差集内部则表明二者发生冲突；而立方体A与C不存在冲突，则原点位于两者的闵可夫斯基差集外部，如图3（b）所示。

2）支撑函数

对于给定的立方体，沿着特定方向d且距离该立方体最远的一点P，称作该立方体的支撑点。即对于立方体C中的任意一点x，存在d·P=max{d·x：x∈C}，则P为立方体C的支撑点。算法利用支撑函数建立一个单纯形，对于给定的2个立方体，支撑函数返回这2个立方体闵可夫斯基差形状中的一个点。构造函数h：

该函数的含义是在闵可夫斯基差集Mk中寻得一点x，使得点x在方向d上的有向投影值h最大，使得函数取最大值的x记作SMk(d)，将SMk(d)定义为立方体的支撑函数，其含义为对于闵可夫斯基差集Mk，将方向d映射到Mk的支撑点。SMk(d)和hMk(d)关系表示为

因此，算法本身并不需要直接计算闵可夫斯基差，而是通过计算SMk(d)函数反映CSO与原点的位置关系，利用立方体A和B可以计算得到：

由于闵可夫斯基差每次都得到相同的点，会大大增加算法复杂度。因此，构造支撑函数的目的在于：通过支撑函数传递一个方向参数，方向不同，得到的点也不同，避免无效计算，同时使得算法迭代产生的单纯形尽可能包含更大的空间区域，加快算法迭代进程。

GJK算法本质是通过在CSO边界上降序迭代，在单纯形上逐步寻找距原点最近的点。在每次迭代过程中会在CSO内部生成一个单纯形，并且保证下一次生成的单纯形的顶点更靠近原点，将第k次迭代中生成的单纯形定义为τk。若将P(τk)定义为单纯形τk上距离原点最近的一个点，该点可以通过Johnson算法计算得到，当P(τk)=P(CSO)时，存在唯一向量χ(CSO)满足：

即找到CSO上距离原点最近的点，当该点与原点的距离为所求最小距离d时，算法结束。

GJK算法迭代过程如下：

初始设置τ0=∅，P(τ0)为CSO中任意一点。

步骤1初始化单纯形τk为CSO中的一个或多个顶点。

步骤2利用Johnson算法计算得到P(τk)。

步骤3若P(τk)为原点O，则表明原点O位于CSO中，即立方体A和立方体B发生碰撞，算法结束并返回“立方体A与B发生碰撞”。否则，转入步骤4。

步骤4对于τk中不包含顶点P(τk)的子单纯形，将其顶点从单纯形中移除；

步骤5令Pk=SMk(-d(τk))为-χ(τk)方向-d(τk)上的支撑点。

步骤6将支撑点与顶点P(τk)进行比较，若支撑点Pk在-d(τk)方向上投影值并非极值点，即‖χ(τk)‖2+SMk(-d(τk)) · (-d(τk))=0，则算法结束并返回“立方体A与B无碰撞”，立方体A和立方体B之间的距离为原点O指向顶点P(τk)的向量长度‖ ‖χ(τk)。否则，转入步骤7。

步骤7 将支撑点Pk加入单纯形τk中，转入步骤2，进行迭代。

1.1.2 无人机飞行冲突网络模型

前文叙述了GJK算法应用于2个立方体的碰撞检测，由于低空空域内无人机以连续状态运行，以GJK算法为基础，将算法推广到判断一段连续时间内两架无人机是否会发生冲突，提出无人机飞行冲突网络模型动态构建算法，应用于多无人机运动场景［22］。

假设低空空域内有多架无人机进行匀速直线随机飞行，选取2架无人机A和无人机B，设定时间区间为[t0，t0+Δt]，其速度分别为vA和vB。Vi表示立方体A和立方体B的顶点，在初始时刻t0，立方体A各顶点位置为SA(t0)=立方体B各顶点位置为SB(t0)={VB0(t0)，VB1(t0)，…，VBn-1(t0)}，m和n表示立方体A和立方体B的顶点数。在[t0，t0+Δt]时间内，立方体A和立方体B的顶点位置在时刻t可表示为

式中：∀t：t=t0+λ·Δt，t∈[t0，t0+Δt]；λ∈[0，1]；i∈{0，1，…，m-1}；j∈{0，1，…，n-1}。

以无人机A作为主动冲突识别对象，设SM为立方体A和立方体B的CSO，在时段[t0，t0+Δt]内，由式（8）和式（9）可得SM的顶点位置为

在一段时间内SM移动构成了近似矩形的区域，如图4所示，其运动轨迹为

图4 [t0，t0+Δt]时间段CSO运动轨迹Fig.4 Trajectory of CSO at time [t0，t0+Δt]

每一个顶点ViMj(t)从t0到t0+Δt形成一条轨迹，在SM移动过程扫描过的区域所有顶点的移动轨迹都是等长的，长度为‖ traM(1)‖。

利用GJK算法进行冲突网络构建的方法是判定一段时间内CSO距离原点的最小距离，CSO的运动具有时空连续性，因此只需判定原点到CSO顶点轨迹的最小距离。若2架无人机未发生冲突，则原点在CSO外部，且与CSO最小距离为边界轨迹到原点的距离；若发生冲突，则原点在CSO内部，且在某2个顶点的运动轨迹之间。因此计算原点与CSO的距离可转化为原点与CSO边界轨迹的距离dO：

原点O与CSO边界轨迹的距离是通过找到合适的^来确定，根据文献［23］，通过割线法进行实验=0.5左右时距离较小，最小距离为

因此，解决问题分成2个步骤：首先找到距离原点最近的CSO顶点轨迹，其次计算原点与最近轨迹点的最短距离。算法伪代码如算法1所示。

算法1 基于GJK的冲突网络构建算法输入：t0，SA(t0)，SB(t0)，Δt，traM(λ)输出：（“未发生冲突” ，λc，dO）或（“发生冲突”）1.k=0， V~k={VA0(t0)-VB0(t0)}2.do 3.（λ^，dO，OM，V~k′，Oin）←Johnson algorithm 4.if Oin then 5.return （“发生冲突”）6.caculate SM(-OM)，S′M(-OM，λ^)7.if SM(-OM)=S′M(-OM，λ^) then 8.V~k+1=V~′k∪{SM(-OM)}9.else V~k+1=V~′k∪{SM(-OM，λ^)}10.end if 11.k=k+1 12.while true 13.λc=λ^； dO=d^O 14.return （ “未发生冲突”， λc，dO）

1.1.3 实验验证

本节设计了2种不同的三维场景配置，分别采用相同大小的立方体和3种不同大小的立方体来表示无人机，来验证基于GJK的冲突网络构建算法的有效性与及时性。

如图5所示，图5（a）展示了20架相同大小的无人机，选取30 m立方体作为无人机表征，以1 km×1 km×0.6 km的空域大小作为实验环境，无人机在空域内进行随机匀速直线飞行，当碰到空域边界或与其他无人机发生冲突时，会随机改变飞行方向，每个立方体的速度方向随机生成，无人机在此空域环境中运行30 s。当2个立方体接触发生冲突时，立方体颜色由蓝色变成红色，当2个立方体分开后，恢复为蓝色。图5（b）展示了3种不同大小的无人机，选取边长200、100、30 m立方体作为3种不同类型的无人机表征，实验选取了3架中型无人机，3架小型无人机，14架微型无人机共20架无人机进行实验。

图5 2种不同场景下的冲突识别Fig.5 Conflict identification in two different scenarios

为了验证无人机冲突网络构建算法的有效性与识别效率，分别针对冲突识别准确率和冲突识别时间2个指标，与三维坐标系下通过成对计算无人机之间的欧氏距离来识别冲突的传统方法进行比较。

在冲突识别准确率比较实验中，无人机的数量从2架不断增加到20架，不同数量无人机分别在三维环境中运行30 s，在该时段内实际发生的冲突数量为N0，算法识别到的冲突数量为N，假设不存在虚假冲突告警情况，定义冲突准确率为Ec=N/N0。在传统基于Reich模型［24］的冲突识别算法中，将无人机安全保护区设置为球形保护区，间隔半径设置为D=0.02 km，但由于无人机种类大小不尽相同，此安全间隔半径设置为满足尽可能多的无人机类型，取各种类型无人机平均安全间隔作为阈值，当无人机距离小于阈值时算法即判定为冲突。为了进一步验证算法性能，对不同算法的准确率进行对比分析，以20架无人机为例，2个分别为相同种类和不同种类的无人机冲突识别场景，实验结果如图6所示。

图6 冲突识别准确率对比Fig.6 Comparison of conflict identification accuracy

在相同粒度场景中，当无人机数量较少时，2种算法的准确率均能够达到100%，随着无人机数量增加，2种冲突识别算法准确率均稍有下降，并趋于稳定在96%以上的较高水平。在相同识别时间基准下，传统算法的准确率与本文算法几乎持平，但由图6（b）可知，在相同识别时间基准，本文算法的准确率远高于传统算法，具有更高的冲突识别效率，在实际应用中具有更快的响应速度。在不同识别时间基准中，由于设定了3种不同大小的无人机，无人机性能不尽相同，其安全间隔距离也不固定，体积较大的无人机安全间隔的需求更大，在体积较大的无人机之间识别冲突时，传统算法设定的安全阈值并不能满足要求，无法有效识别到真实冲突的发生，本文算法由于不需要设定阈值，适用于多种无人机类型，冲突识别准确率稳定在95%以上，而传统算法在不同种类的无人机冲突识别场景中的准确率显著降低。在实际应用场景中，无人机的种类往往不止一种，是多种不同大小性能的无人机在空域中进行飞行，本文提出的基于GJK的冲突网络构建算法可在多种不同类型的无人机运动场景中进行更为有效的探测。

图7所示为不同粒度场景下不同算法的冲突识别时间对比情况。随着无人机数量的增加，传统算法的冲突识别时间呈近指数增长，本文提出的基于GJK的冲突网络构建算法增长呈线性增长，增长趋势较为缓慢，所提算法具有高效性。

图7 冲突识别时间对比Fig.7 Comparison of conflict identification time

1.2 特征提取及分析

1.2.1 飞行冲突网络特征提取

采用复杂网络理论［25］，将无人机群体视作复杂网络，其中无人机个体为网络的“节点”，无人机之间存在的冲突为网络的“边”。运用基于GJK的冲突网络构建算法，对复杂低空环境中的无人机冲突连边进行动态识别，在此基础上通过复杂网络的相关概念分析低空空域运行态势。本文基于复杂网络理论提出以下3个指标，对空域无人机群体的冲突网络特征进行分析。

1）冲突数量

根据复杂网络中“度”的概念，将Ki定义为与无人机节点i存在冲突关系的无人机数量，表示为

式中：eij为0-1变量，若无人机节点j与i直接相连，则取值为1，否则为0。

2）冲突风险等级

为了使复杂网络更接近于无人机飞行场景，通过无人机之间的相对距离和相对速度来表达无人机的真实关系，即2架无人机接近彼此的速度越快，越容易发生冲突，无人机冲突等级便越高。定义无人机i与无人机j之间的冲突风险为

式中：rij为无人机i和j的相对速度；xij为无人机i和j之间的相对距离。

将无人机i的冲突风险等级Ei定义为

3）聚集系数

复杂网络中聚集系数表示某个节点相邻的2个节点彼此也相邻的概率，在无人机冲突场景中表示某架无人机周围的无人机密集程度，在无人机群一个冲突数量为Ki的无人机节点i的聚集系数Ci定义为

式中：Ni表示无人机节点i的Ki个存在冲突的无人机之间实际存在的冲突的边数，即无人机i的Ki个相邻无人机之间实际存在的邻居对的数目。聚集系数反映了无人机i附近的拥挤程度即冲突发生的可能性。

1.2.2 飞行冲突网络特征分析

设置低空空域环境中共有50架无人机，采用冲突网络构建算法建立冲突节点连边，对无人机运行状态构成的复杂网络进行网络演化，网络每30 s演化一次，共演化30 min，即网络共演化R=60次，每次演化完成时根据网络中节点的数量和无人机位置关系，获得节点的连接关系构建复杂网络模型。演化第0、5、10、30 min的网络如图8所示。

图8 空域中无人机网络演化过程Fig.8 Evolution of UAV networks in airspace

低空空域内的无人机群体每进行一次演化，提取冲突网络中各无人机节点的位置和速度，计算每一时刻空域内所有无人机指标的平均值，进而度量飞行冲突网络的各个特征指标，便可得到各指标的时间序列，如表1所示。通过仿真发现，网络演化过程中每架无人机平均与2～4架无人机发生冲突，冲突风险等级集中分布在6～7范围内，聚集系数集中分布在0.5～0.6范围内，飞行冲突网络特征演化过程如图9所示。

表1 网络演化特征指标Table 1 Characteristic indicators of network

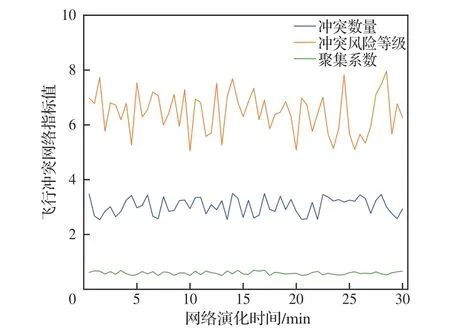
图9 飞行冲突网络特征演化Fig.9 Evolution of flight conflict network characteristics

2 基于数字栅格的无人机飞行冲突精细探测

无人机运营者可根据任务目的和飞行计划等信息进行无人机飞行路径规划，无人机则可按照预先设定的轨迹实施飞行活动。在实际运营过程中，因存在潜在的飞行计划冲突，导致预先设定的飞行航迹可能无法执行，而无人机运行安全与效率水平亦随着潜在冲突的增加而降低。因此，本节采用数字栅格方法，将无人机的物理航迹点信息映射到以栅格编码为索引的数字栅格中，对无人机潜在冲突进行探测。

2.1 空域数字栅格剖分

空域栅格化是指基于栅格化思想，建立空域栅格单元剖分方法，构建基于栅格索引的空域系统，从而支撑空域系统表征、规划、管理与评估研究的一种空域离散化处理方法。本节面向低空空域无人机运行管理需求，建立了离散栅格框架下的低空空域数字栅格剖分与编码设计方法。

全球空域空间栅格编码［26］以地球的南极点为基准点，构建了全球栅格系统参考位置，在空域空间栅格剖分的基础上建立了栅格编码规则。该方法采用基于经纬度整数规则的地球椭球面剖分方法，即以经纬度的“度-分-秒”整数形式进行椭球面的空间分区划分，这种划分实质是一种大地坐标系的度量参数离散化描述方法。

定义空域栅格的基本原则：首先，要统一基准，对尺度范围内的空域建立统一的标准；其次，要做到可以相互转换，兼容地理位置栅格码以及全球定位系统（Global Position System， GPS）和北斗等既有标准，实现位置与编码的相互转换；最后，要做到高效实用，以地理经纬栅格为原型，划设不同层级的空域，基于空域管理需求，在不同层级的栅格建立应用规范。根据上述原则进行低空空域离散建模，将连续空间离散为基本空域，用空域编码取代经纬度标识空间位置，以低空空域编码为索引，建立描述低空空域的数据结构，管理低空空域内活动。

由于无人机多数在中低空空域内运行，机动性较高，因此栅格编码模型采用地球球面和高度分开处理的方法，平面编码和高度编码均采取“Z”形编码，将栅格左下角位置点定义为栅格坐标原点，分别在地理经纬度空间和高度空间内定义栅格。基于地理空间经纬度，进行球面栅格划分，共划分8个层级的递归栅格。针对不同的层级栅格，建立栅格划分矩阵，n为栅格划分层级，取值1～8，设定栅格所在划分矩阵的行数和列数为(pn，qn)，划分矩阵可表示为

在地球墨卡托投影坐标系统上，首先以经纬度15°为剖分粒度，将地球的椭圆面进行完整划分，具体情况如图10所示。

图10 栅格剖分方法Fig.10 Grid splitting method

采用字母进行栅格单元编码，由于数字0和1容易与字母O和I混淆，因此不采用O和I进行编码。在15°大小的第1级栅格单元基础上，按照1°剖分间隔进行剖分，形成1°大小的第2级栅格单元，对1°大小栅格单元采用二分法进行剖分，形成经纬度30′大小的第3级栅格单元。在经纬度30′大小栅格单元基础上，进行第4级和第5级栅格单元的剖分，第4级栅格采用键区标识剖分至10′大小单元，第5级栅格采用象限标识剖分至1′大小单元。在经纬度1′大小栅格单元基础上，再进行第6级、第7级、第8级栅格单元的剖分。根据低空无人机运行特点，将低空空域剖分至栅格大小为6″、3″和1″。具体划分层级如表2所示。

表2 低空空域栅格划分层级Table 2 Airspace grid classification hierarchy

以第8级栅格编码生成5 km×5 km×0.2 km大小的低空空域栅格环境，实验结果如图11所示。

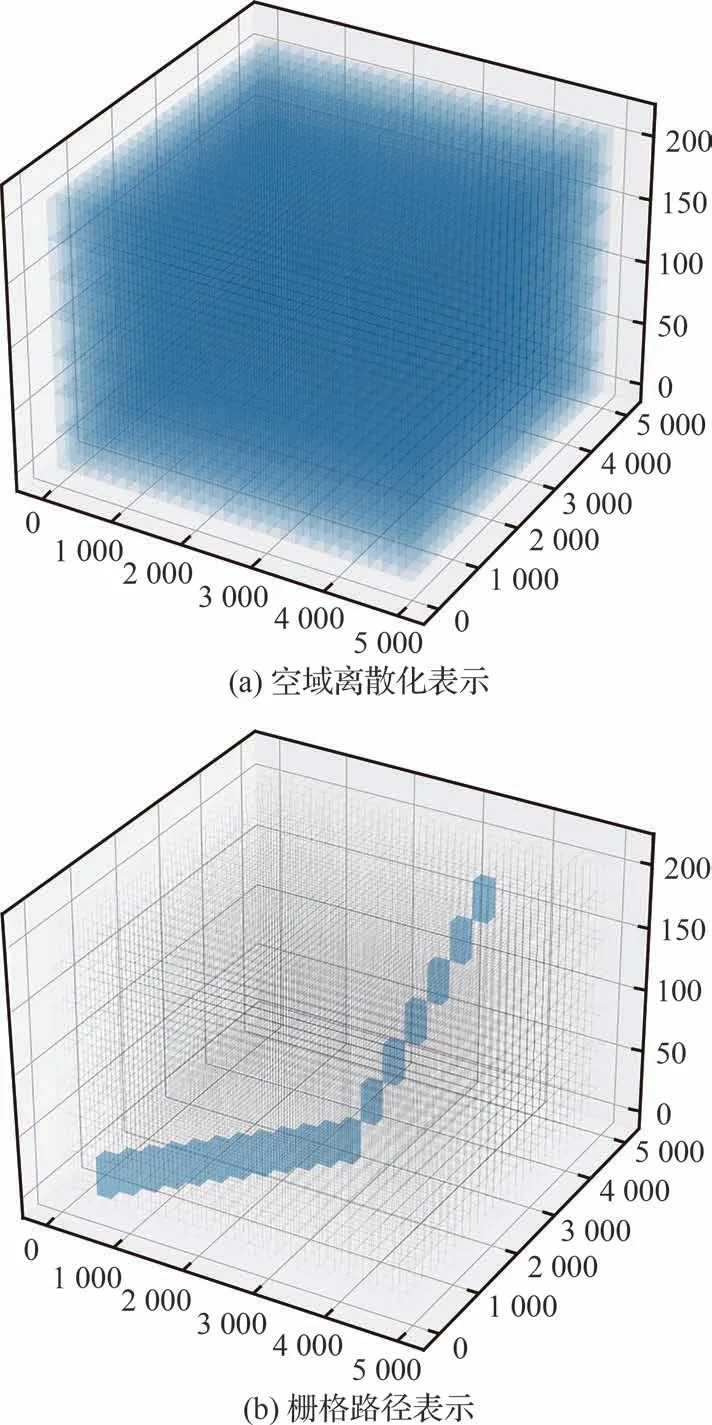
图11 空域栅格化及路径栅格表征Fig.11 Airspace gridding and path raster representation

2.2 空域数字栅格编码

水平位置编码依托经纬度，采用2.1节提出的剖分方法进行编码。对于高度编码，基于单个栅格进行编码，本文以30 m为粒度向上拓展，生成符合空域最高高度的栅格大小。整体八级编码呈现形式为“ab-cd-e-f-gh-ij-k-l”。其中，前2位代表第1级编码，第3位和第4位代表第2级编码，第5位代表第3级编码，第6位代表第4级编码，第7位和第8位代表第5级编码，第9位和第10位代表第6级编码，第11位和第12位分别代表第7级和第8级编码。采用二进制方法，对高度进行单独编码。“度”级体块编码用d表示；“分”级体块编码用m表示；“秒”级体块编码用s表示，编码组成单元层级可以表示为“dd-mmmsss”。

地理位置的经纬度坐标信息(Lng，Lat)通过式（21）～式（22）进行编码转换：

式中：经度编码和纬度编码分别用CodeLng和CodeLat表示；n表示编码层级；gridsizen表示第n层级栅格粒度大小；Lngd、Lngm和Lngs分别表示经度坐标中的度、分和秒；Latd、Latm和Lats分别表示纬度坐标中的度、分和秒。

针对不同的应用场景，本文所构建的栅格编码可以与栅格划分矩阵进行相互转换。

1）由栅格编码转化为划分矩阵。

首先根据栅格编码确定栅格划分层级n，根据栅格编码计算出栅格坐标原点的经纬度坐标(Lngn，Latn)，确定在该层级下栅格划分的经纬度粒度间隔ΔLng和ΔLat，根据式（23）和式（24）进行转换，得到目标栅格所在的划分矩阵位置。

式中：pn和qn表示第n层级下栅格所在划分矩阵的行数和列数，与式（20）中的内涵一致。

2）由划分矩阵转化为栅格编码。

首先根据栅格编码确定栅格划分层级n，确定在该层级下栅格划分的经纬度粒度间隔ΔLng和ΔLat，根据式（25）和式（26）计算得到栅格原点的经纬度坐标。

然后，根据经纬度坐标，利用式（21）和式（22）计算得到栅格编码。

空域栅格化为低空无人机空中交通管理提供了一种新的位置参考基准，通过数学模型在计算机信息空间内完成了对物理空间的数字化重构，距离运算可以转化为编码或者划分矩阵之间的运算，可以更加快速和准确地判断无人机之间的空间位置关系。

2.3 基于数字栅格的冲突探测模型

在空域栅格编码的基础上增加时间维度，构造数字栅格单元，时间编码采用数字编码，以0为开始时间，运行的最长时间为最大时间上限，按照图10的栅格剖分方法，整体八级编码呈现如图12所示。

图12 低空空域数字栅格编码格式Fig.12 Digital grid coding format in low altitude airspace

通过特定的空间区域和时间范围的时空编码来表示无人机的时空信息，每个空间内的物体均可用一个或多个栅格表示，建立一定空域内的多级时空索引。根据划设的实验空域对数据表主键进行初始化，进行排序后的时空栅格编码与具有特定时空属性的栅格密切相关，因此将其设置为数据表中的主键。

当一个空间栅格中存在一架无人机时，对应代码记录为1；否则设置为0。时间信息将记录在数据库表中的每一行，并具有开始时间戳和结束时间戳，以此表示某无人机在特定时间段在该空间栅格内。因此，通过数字栅格索引，可以将冲突探测的复杂成对计算问题简化为空间数据库查询问题。

为了满足多级查询的需要，建立图13所示的多表查询策略，通过多个数据库表管理记录特定空域内的无人机信息。每个数据库表中只存储某一级别编码对应的数据，并且父代编码具有指向子代编码所在数据库表的指针，以此保证当查询完本级编码后，如需要进一步详细查询，可以直接链接到下一级编码所在的数据库表。其中每行数据库表记录了所研究空域中的一个栅格单元，且数据库表中的行数与空域中栅格单元的总数相同。

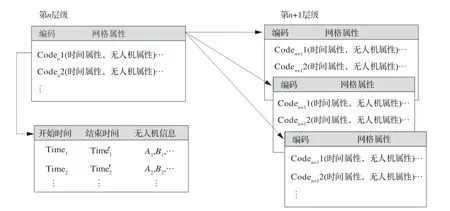
图13 低空空域网络多级数据库表查询策略Fig.13 Multi-level database table search strategy of low-altitude networks

基于数字栅格结构建立多层级查询，可使冲突检测不再拘束于同一层级的判断，当2架无人机在同一栅格内即可判断为存在冲突；除此之外，在冲突检测过程中，每一级编码均具有各自的子代编码与父代编码，很好解决了不同大小栅格的冲突检测问题，同时无人机轨迹数据作为新增数据进行栅格编码后插入至数据库表中，以此减少冗余计算。当用较大粒度栅格表示的中型无人机与用较小粒度栅格表示的微型无人机发生冲突时，由于两者所在栅格层级不同，故两者编码也不会相同，此时通过父代与子代编码的关系进行判断，根据两者是否是包含关系判断两架无人机是否发生冲突。

2.4 算法流程

假设无人机在某段时间[t1，t′1]内通过一系列编码栅格表征飞行路径，N为最低层级，其中每个栅格对应一个空间编码Code，则每个栅格的时空信息可以表示为{Code，[t1，t′1]}，无人机的飞行路径可以记录为一系列栅格集合。对于每个栅格，在同一级别上可以记录多个空间栅格编码，并且在同一栅格上可以记录多个对应的时间间隔，编码层级变量i开始从1到N-1进行遍历，对于每个层级i均需获得编码Code的父代编码F(Code)i。对于具有时间属性的所有i级空间栅格编码，若对应的数据库表为空，则不存在冲突；否则应根据父代与子代编码进行冲突判断，当层级为n时，可根据该层级的编码直接进行比较，来判断栅格的位置关系，编码相同则判定为冲突。每架无人机的飞行轨迹栅格可赋值为

式中：UAVA表示无人机编号；[t1，t′1]表示无人机占用该栅格的时间。

根据空域栅格的时空属性，若在同一空间栅格中有两个或以上的赋值，则表明有多个无人机飞行计划会占用此栅格区域，需要判定其时间上是否存在冲突，若时间上存在冲突，则可以判定在该栅格处存在飞行冲突，需重新调整飞行计划。若无人机大小不同，则首先要判断其空间编码是否存父子代关系，再判断时间上是否会发生冲突。算法步骤如下：

步骤1假定空域内存在n架无人机，每一架无人机的飞行计划轨迹被离散为M个时间片，因此空域内无人机飞行轨迹可表示为n×M元素的矩阵A，同时构建辅助矩阵B。

步骤2将无人机飞行空域离散为栅格。

步骤3通过式（21）和式（22）将每架无人机的飞行轨迹点由经纬度转换为栅格编码集合。

步骤4将每一架无人机飞行计划中预测轨迹点对应的栅格单元存入矩阵A，并在辅助矩阵B中存入无人机编号信息。

步骤5扫描检索矩阵A中的各个元素，若发现存在相同编码或存在父子代关系的编码，则判定在该栅格处发生冲突。

步骤6读取存在冲突的栅格信息，通过索引从矩阵B中确定存在冲突的无人机编号信息，对相关无人机进行飞行计划调整。

2.5 仿真验证

为探究数字栅格方法的冲突检测效率，本节设计实验对传统三维坐标检测方法与数字栅格数据检索方法下的无人机飞行冲突探测总时间进行了对比。将冲突探测总时间定义为探测到空域环境中第一次发生冲突至最后一次发生冲突之间的时间间隔。基于三维坐标的冲突检测方法通过成对计算任意2架无人机之间的欧几里德距离，并将计算得到的距离与设定的阈值进行比较来检测冲突。本节针对100～1 000架逐渐递增的无人机实验样本，其四维航迹点根据飞行计划仿真生成。将传统方法下的无人机安全保护区设置为球形保护区，间隔半径设置为D=0.02 km，时间步长设置为Δt=0.1 s。上述2种方法下的无人机冲突探测时间对比情况如图14所示。

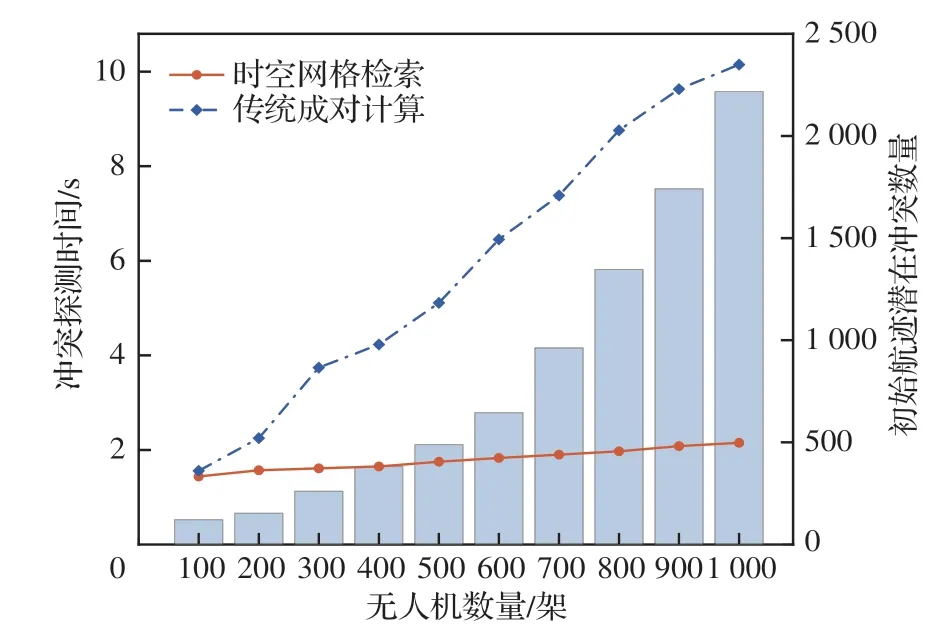
图14 不同方法下的无人机冲突探测效率对比Fig.14 Conflict detection efficiency of different methods

可以看出，随着无人机数量的不断增加，初始航迹存在的潜在冲突数量亦随之增加，并且2种方法对应的冲突探测总时间均呈现增长趋势。当无人机数量＜200架时，2种方法冲突探测效率相当；随着无人机数量的继续增加，传统成对计算方法的冲突探测时间增长趋势更加明显，而基于数字栅格检索方法的冲突探测时间增长则较为平缓，基本稳定在2 s左右，本文方法相比传统方法，可将探测总时间减少78.4%。显然，基于数字栅格的方法明显优于传统的成对计算方法，具有较高的无人机冲突探测效率与稳定性。

为进一步探究基于数字栅格的冲突探测算法效率，现针对300、500、1 000架的无人机飞行场景进行算法对比，为减少仿真随机性对结果的影响，实验采取3种固定场景，对预生成的固定航路进行冲突探测。图15所示为本文提出的基于数字栅格的算法与速度障碍法、传统基于Reich模型的成对比较算法在冲突探测效率方面的对比情况。

图15 固定场景下的不同算法冲突探测效率对比Fig.15 Conflict detection efficiency of different algorithms in fixed scenarios

由图15可知，在无人机数量相对较少的场景中，3种算法的冲突探测效率差异不大，本文提出的基于数字栅格的算法时间略快。随着无人机数量的不断增加，本文所提算法的冲突探测时间明显小于其他2种算法，速度障碍法虽略好于传统成对比较的方法，但其探测时间仍然较长。因此，本文提出的基于数字栅格的冲突探测算法效率较高，相比其他算法具有明显的优势。

3 基于网络演化的无人机飞行冲突最优解脱

在基于数字栅格的无人机飞行冲突探测的基础上，本节以无人机冲突数量最少和运行成本最低为优化目标，构建了考虑优先级的无人机冲突解脱多目标混合整数优化模型，对无人机飞行冲突解脱策略进行了最优求解。

3.1 模型构建

3.1.1 模型假设

1）将无人机简化为质点，忽略运动姿态和机动性能对冲突管理的影响。

2）不考虑无人机的悬停操作。

3）在未探测到冲突风险和未接收到飞行调整指令之前，无人机始终沿直线飞行。

3.1.2 决策变量

采用3种机动方式对存在潜在冲突的无人机航迹进行调整，分别是航向调整、高度调整和速度调整，因此引入3个决策变量ωi、hi和υi分别表示对无人机i采取的航迹调整方式，将决策变量整合到一个决策向量κi=[w h υ]，κi表示对无人机i航迹进行的调整。

1）设定存在N条栅格离散无人机轨迹，允许设置的虚拟航路点数量即为时间片数量M，无人机i的初始航段的栅格数量为Li，0，虚拟航路点位置的栅格编码为，对于空域内所有无人机航迹虚拟点构成的栅格编码集合为w=(ω1，ω2，…，ωN)。图16为M=2时设置虚拟航路点生成的航迹。

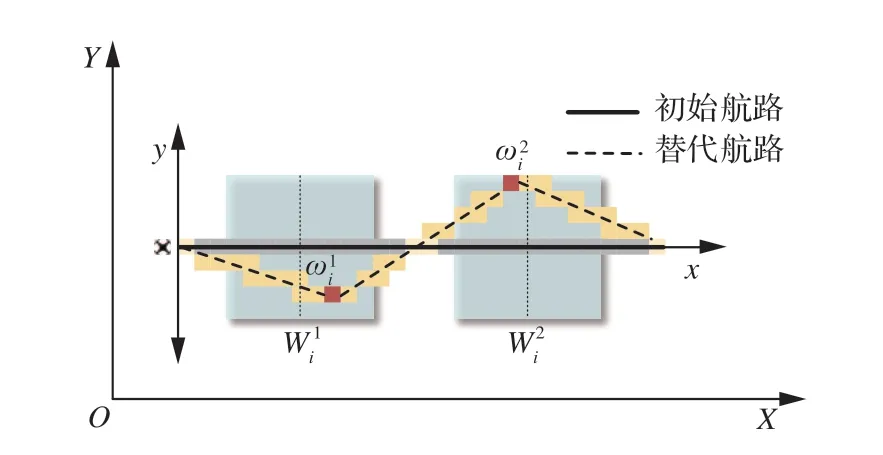
图16 M=2时设置虚拟航路点生成的航迹Fig.16 Trajectory generated by virtual waypoints at M=2

2）在栅格化空域下，设定无人机i的初始飞行高度层为Hi，0，hi表示无人机进行高度调整时高度改变的栅格数量，改变高度后飞行高度层变为Hi′=Hi，0+hi，所有无人机高度调整栅格改变数量构成集合h=(h1，h2，…，hN)。

3）设定无人机i的初始飞行速度为Vi，0，vi表示无人机进行速度调整时的速度改变量，改变速度解决冲突后飞行速度变为V′i=Vi，0+vi，空域内所有无人机速度调整量构成集合v=(v1，v2，…，vN)。

3.1.3 目标函数

1）冲突数量

根据前述构建的基于数字栅格的冲突探测方法，通过离散化低空空域和四维坐标将每架无人机i的航迹点集合Pi映射到相应的编码栅格结构中，该方法只需判断无人机航迹采样点Pi，g对应的数字栅格是否存在其他无人机的航迹采样点。若存在，则判定无人机i在航迹采样点Pi，g处存在一次冲突。空域内所有航迹之间的冲突数量可表示为

式中：Φi，g表示无人机i在g点发生冲突。

2）运行成本

从低空空域运行角度考虑，无人机按照计划航迹点集合进行飞行的成本应尽可能小，输入的无人机航迹点集合是针对单体最优的航迹，若探测到无人机之间的冲突，则无人机会采取机动策略导致飞行前计划航迹改变，使无人机的飞行距离增加，或当采取速度调整策略时虽不会增加额外的飞行距离，但无人机的飞行时间相较于飞行前的计划航迹会有所增加。因此，从飞行时间、经济成本等方面考虑，优化目标为无人机实际飞行解脱的航迹相较于原飞行前无人机航迹的航迹成本增加最少，航迹成本包括解脱航迹与飞行前计划航迹之间的偏差、解脱后航迹的到达起飞时间的改变量2个部分。空域中所有无人机的总成本（标准化后的无量纲数值）为

式中：R(κi)和T(κi)分别表示无人机i航迹和时间偏移成本。

本文考虑冲突解脱优先级，设置权重系数η∈(0，1]，将所有无人机根据优先级排序设置不同权重大小，对于解脱优先级高的无人机，设置较低权重尽可能减少其飞行成本，进行优先解脱；对于优先级较低的无人机，尽可能减少其航迹改变，设置较大权重系数，权重差设置为1/N，故优先级从高到低成本系数为η=1/N，2/N，…，N/N=1。本文基于优先级对所有无人机飞行成本进行加权求和，得到考虑优先级的空域中所有无人机总成本为

航迹偏移量主要考虑由于解脱策略造成的航迹改变，使解脱后的航迹与飞行前的计划航迹产生偏差，定义为每架无人机的航迹点集合从第一个至最后一个航迹点所有冲突解脱结束后，实际的冲突解脱航迹和原飞行前的无人机计划航迹之间的栅格数量之差。每架无人机的航迹偏移成本可表示为

式中：i=1，2，…，N表示无人机的数量；j=1，2，…，Mk表示无人机i航迹集合中第j个航迹点；Mk为无人机i航迹集合中虚拟航迹点数量；di，j表示无人机i在第j个航迹点时，实际冲突解脱航迹点与原飞行前无人机计划航迹采样点的栅格数量差。

时间偏移成本主要考虑由于解脱航迹造成的总的运行时间的偏移量，使解脱后的航迹运行时间与飞行前的计划航迹的运行时间之间产生的偏差，定义为无人机i的解脱航迹运行时间和原飞行前无人机计划航迹运行之间的偏差量，可表示为

式中：i=1，…，N表示无人机的数量；Δti表示无人机i的解脱航迹运行时间和原飞行前无人机计划航迹运行之间的偏差值。

3.1.4 约束条件

1）允许的最大水平路径长度

每架无人机i的初始航段长度（占用栅格数量）Li，0，设ℓi为无人机i的最大允许航线长度扩展系数，0≤ℓi≤1，为了限制航线长度的延长，无人机i的备选航线水平剖面必须满足：

式中：Li(ωi)是由ωi确定的替代航迹的长度（占用栅格数量），因此该约束可通过限制航路点位置来满足。

2）允许的水平航路点位置

为了限制搜索空间，防止大角度转弯，控制路径长度的延长，因此对每个虚拟航路点的可能位置进行了限定。对于每个轨迹i和第m个虚拟航路点，无人机在x和y方向上的偏移分量Wmi，x和Wmi，y表示为

式中：0≤α≤1，0≤β≤1为用户自定义参数；表示向下取整运算。

为了获得规则的航迹，相邻2个航迹点的x方向分量不能重叠，即

由式（36）可得出，选取的βi应满足βi＜1/[2(M+1])。因此为了限制无人机的最大拓展航路，应满足：

3）允许的高度层改变

由于偏离偏好航迹的飞行高度可能会导致额外的运行成本，同时考虑无人机自身性能约束，因此需要限制无人机i的高度改变量。引入低空空域高度层的概念，将高度离散处理，无人机i所有可行的高度层改变量集合ΔHi表示为

式中：hi，max为无人机i允许最大高度层改变量。

4）允许的速度改变

由于受自身性能约束和飞行环境影响，无人机存在最大和最小飞行速度限制，无人机i受自身性能约束的速度限制表示为

综上所述，本文考虑的动态冲突解脱问题可以表示为以下的多目标混合整数优化问题：

3.2 算法设计

无人机冲突解脱问题的复杂度随决策变量数量的增加以几何级数增长，决策变量之间存在强耦合关系，且本文提出的冲突解脱模型是非线性不可微分的复杂模型，难以在短时间内得到目标解，因此本文采用元启发式算法进行求解。无人机冲突解脱是一个多目标优化问题，鉴于非支配排序遗传算法（Non-Dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ）在非支配排序、拥挤距离排序、运行速度及解集收敛性等方面的诸多优点，采用NSGA-Ⅱ算法对所建优化模型进行求解。

1）编码设计

染色体编码对算法求解效率至关重要，本文采用整数编码方式对染色体进行编码，每条染色体代表所有无人机航迹方案；染色体长度表示所有无人机的总架数，染色体内每个基因位置表示无人机各航迹点所做的航向、高度和速度调整。染色体基因编码实例如图17所示。

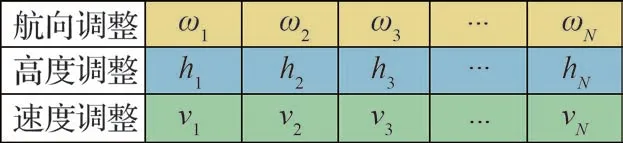
图17 染色体基因编码示意图Fig.17 Diagram of chromosomal gene coding

2）快速非支配排序

快速非支配排序是依据种群个体的帕累托支配关系对种群分层，为了引导搜索向帕累托最优解集方向进行。快速非支配排序的思想是给每个个体p都赋予3个参数：Sp、np和rankp，其中，Sp为种群中被个体p支配的个体集合；np为种群中支配个体p的数量；rankp为个体p的帕累托层级。快速非支配排序的操作过程如下所示。

步骤1遍历种群计算每个个体的参数S和n。

步骤2初始化非支配序，即帕累托层级，令rank=1。

步骤3根据帕累托支配关系，找到种群中所有不被其他个体支配的个体，组成非支配解集并将其所有个体帕累托层级赋值为rank，并从整个种群中剔除。

步骤4判断种群个体数量，若数量为零，则非支配排序结束；否则，rank=rank+1，返回步骤3。

3）拥挤距离

为了保证种群的多样性，通过优先选择拥挤距离较大的个体，可使计算结果较均匀分布，避免个体都集中于某一处导致无法得到帕累托最优解集。计算个体i拥挤距离disi步骤为：

步骤1为帕累托层级中的每个个体增加拥挤度属性，初始化disi=0。

步骤2遍历每个rank中的个体i，将处于边缘位置的个体的拥挤距离赋值为+∞，处于中间位置的个体拥挤距离计算公式为

3.3 优先解脱流程

在冲突解脱过程中，引入优先级概念，优先级高的无人机优先采取机动策略避让优先级低的无人机，通过复杂网络的相关概念确定空域中运行无人机的冲突解脱优先级。基于1.2节提出的飞行冲突网络特征，以式（42）～式（44）定义无人机在解脱顺序时的优先级原则，得到无人机解脱顺序。

原则1无人机平均冲突数量，计算公式为

原则2无人机平均冲突风险等级，计算公式为

原则3无人机平均聚集系数。计算公式为

在本文全局冲突解脱场景中，优先级高的无人机优先计算解脱方案，优先级低的无人机将已解脱的无人机视为移动障碍物限制，保证已解脱的无人机不会与优先级低的无人机发生冲突。定义障碍物集合Ω，障碍物优先级SΩ=0；无人机i的优先级Si=1，2，…，Smax；S越小表明无人机优先级越高。冲突解脱流程具体如下所示

步骤1获取无人机信息，提取空域内所有无人机的水平位置、高度、速度以及航向，根据2.3节中的方法进行冲突探测，得到所有存在潜在冲突的航迹集合G。

步骤2令S=1，生成障碍物集合Ω。

步骤3计算优先级最高的无人机对应的冲突解脱策略。

步骤4S=S+1，若S＞Smax，则已遍历所有优先级，冲突解脱算法结束。

步骤5将Si＜S的所有无人机视作障碍物，加入障碍物集合Ω，求解当前优先级无人机对应的冲突解脱策略，返回步骤4。

3.4 仿真验证

3.4.1 实验设计

基于Python 3.8环境，对多无人机冲突解脱过程进行仿真分析，根据前述实验场景，基于数字栅格的冲突探测模型，对空域中50架无人机进行冲突探测，结果表明初始航迹存在的冲突数量为93，空域内所有无人机的运行成本为5 916。根据上述算法对其中存在冲突的无人机航迹进行冲突解脱，以验证本节提出的冲突解脱算法的有效性。本小节采用NSGA-Ⅱ算法对模型进行求解，随机产生规模为200的初始种群，进行进化迭代求解。根据常见的无人机型号，以大疆经纬M100性能参数作为参考，多无人机冲突解脱模型参数设置如表3所示。

表3 无人机冲突解脱模型参数设置Table 3 Parameter of UAVs conflict resolution model

NSGA-Ⅱ算法参数设置如下：设定种群大小为200，最大进化代数200代，交叉概率0.9，变异概率0.05。在上述基准参数下，进行仿真实验，所有实验结果皆基于10次独立运行。

根据飞行状态网络连边的建立规则，采取数字栅格的冲突探测算法，根据设定的50架无人机初始飞行计划，当2架无人机之间存在潜在飞行冲突时，则认定无人机之间存在联系，并建立连边，基于复杂网络的无人机初始冲突分布如图18所示。

图18 无人机运行状态网络Fig.18 Network of UAVs operation

3.4.2 结果分析

设置50架无人机，初始航迹存在的冲突数量为93个。在3种不同优先级排序下，经过10次独立运行，算法分别得到26、23、20个非支配解，如图19所示。对于本节提出的多目标冲突解脱问题，算法得到的总运行成本和总冲突数量最小的非支配解对应的优化性能均高于初始解，由此可知NSGA-Ⅱ算法能够有效解决本仿真案例中的初始航迹潜在飞行冲突并降低无人机运行成本。

图19 不同优先级原则所得到的非支配解Fig.19 Non-dominated solutions resulting from different priority principles

为了验证不同优先级原则在解决航迹冲突时的效率，对比了3种不同原则下冲突数量和运行成本的收敛情况，如图20所示。结果表明，采取原则2和原则3均可有效解脱冲突且原则2收敛更快，原则1则不能完全实现的无冲突解脱。另外，基于原则2的解脱策略可以更好地降低运行成本。综上，原则2在冲突管理算法求解效率方面优于原则1和原则3，能够更好地实现多无人机全局无冲突解脱和低成本运行。

图20 不同优先级原则下冲突数量和运行成本算法收敛变化Fig.20 Conflict number and operation cost algorithm convergence changes with different priority principles

表4所示为NSGA-Ⅱ算法的优化结果。比较分析3种不同的优先解脱原则在相同初始条件下解的质量，原则2和原则3在设定的实验环境中可以获得全局无冲突解，同时基于原则2进行算法设计可以更好地降低全局无人机运行成本。在算法求解时间方面，三者比较相近，但由于原则1基于每架无人机的冲突数量进行优先级排序，对初始解的质量要求较高，算法收敛较慢，因此花费的时间最长，原则2和原则3时间相近，但原则2进行优先级排序时计算复杂度较低，因此算法求解时间略快于原则3。

对考虑优先级和不考虑优先级的冲突解脱仿真结果进行对比分析，设定冲突风险等级为优先级排序原则，选取冲突数量最小的非支配解与不考虑优先级的冲突解脱策略，对高度改变、水平航迹偏移量和速度改变进行成本比较分析，结果如图21所示。图中考虑优先级是指采用平均冲突风险等级定义的无人机解脱优先级，不考虑优先级是指不设置无人机解脱顺序对空域内无人机进行机动调整。

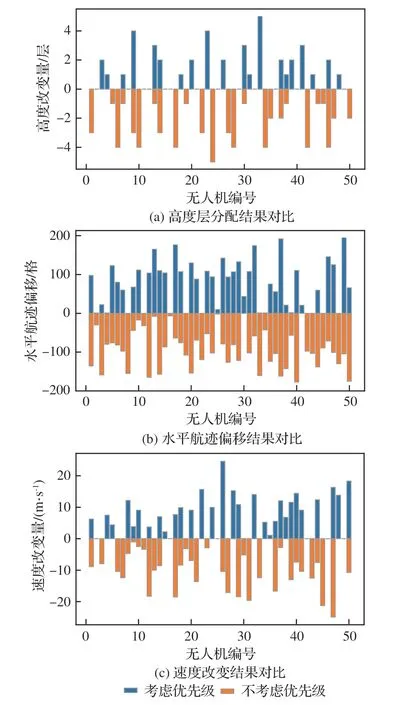
图21 考虑优先级与直接解脱成本对比Fig.21 Cost comparison of priority and direct resolution

根据图21可知，以冲突风险等级为优先级排序原则进行高度层调整相比不考虑优先级可以少调整21个高度层，平均每架无人机高度层调整值减少了32.8%；水平航迹调整相比不考虑优先级少调整991个栅格，平均每架无人机水平调整值减少了21.4%；速度调整相比不考虑优先级少调整51.3 m/s，平均每架无人机水平调整值减少了14.6%。通过对比分析可知，本文提出的考虑优先级的冲突解脱方法使得无人机的机动解脱成本更低，结合高度调整、速度调整和航向调整3种不同的解脱方法，可以更好地利用低空空域资源，降低无人机运行成本，提高冲突管理效率。