具有无症状感染者和病毒变异的传染病模型

范佳欣，孙福芹

具有无症状感染者和病毒变异的传染病模型

范佳欣，孙福芹

（天津职业技术师范大学 理学院，天津 300222）

研究了一类具有无症状感染者和病毒变异的传染病模型．计算了模型的基本再生数，求出了模型的无病平衡点和地方病平衡点．根据Jacobi矩阵特征根的符号，利用Lyapunov函数法，分析了基本再生数不同取值时无病平衡点和地方病平衡点的稳定性情况．通过数值模拟对结论进行了验证．

无症状感染者；病毒变异；传染病模型；稳定性

传染病模型是数学在生物学中应用的一个途径，为人类了解传染病特性提供了一定的帮助[1-8]．近几年爆发的新冠肺炎疫情再次引起了人们对于传染病的关注，新冠病毒自身存在的复杂的变异情况是新冠疫情蔓延广泛而持久的一个重要原因．为了更好地了解存在病毒变异的传染病的传播情况，需要对具有病毒变异情况的传染病模型进行研究．文献[9]对具有病毒变异的SEIR传染病模型进行了分析．而在新冠肺炎疫情中，存在不表现出临床症状，却能够传播感染的无症状感染者，这与潜伏期患者不同，这样的特性也将对疫情的传播产生一定的影响．本文在具有病毒变异的传染病模型基础上，考虑无症状感染者对于传染病传播的影响，建立一类具有无症状感染者和病毒变异的传染病模型，并分析其平衡点的稳定性．

1　模型的建立

基于病毒发生变异情况的传染病模型，考虑无症状感染者对病毒传播的影响，建立一类具有无症状感染者和病毒变异的传染病模型，即

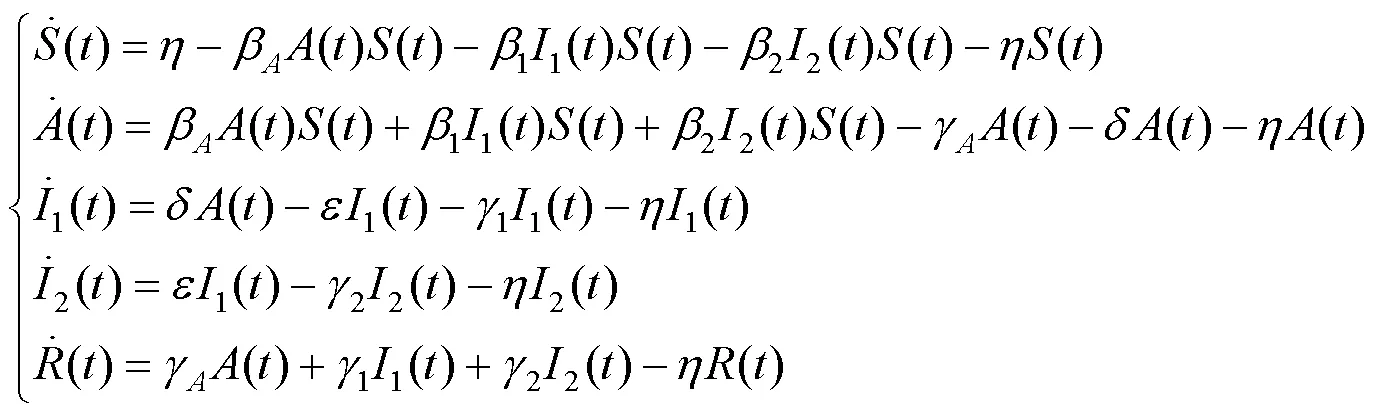
式中：分别为时刻易感人群、无症状感染人群、病毒变异前的感染人群、病毒变异后的感染人群和移除人群在总人群中的占比，无症状感染者是指表示不表现出临床症状，但能够传播感染的传染病患者；为出生率和自然死亡率；，，分别为无症状感染者、病毒变异前的感染者和病毒变异后的感染者的有效接触率；，，分别为无症状感染者、病毒变异前的感染者和病毒变异后的感染者的移除率；为无症状感染者的症状发作率；为病毒变异前的感染者转换为病毒变异后的感染者的比率．模型（1）的流程见图１，初始条件为，并属于集合．

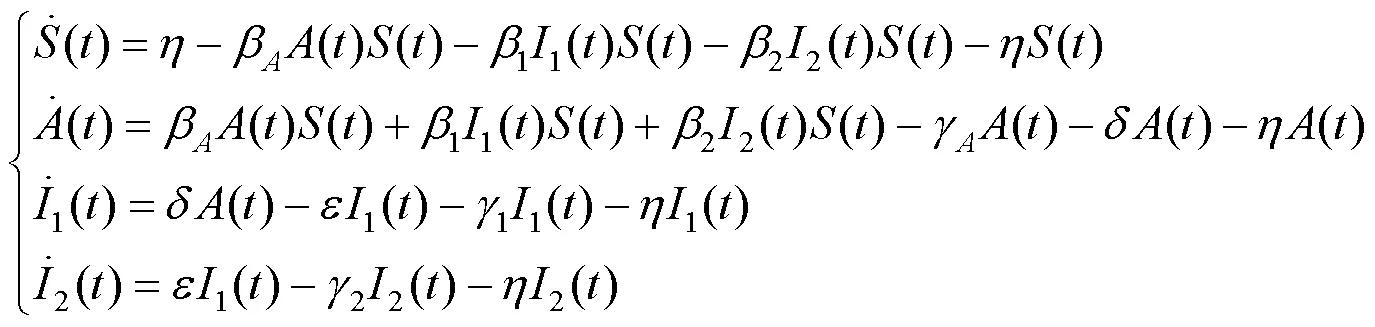
2　基本再生数与平衡点的存在性

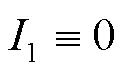
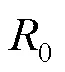
3　平衡点的稳定性

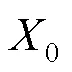
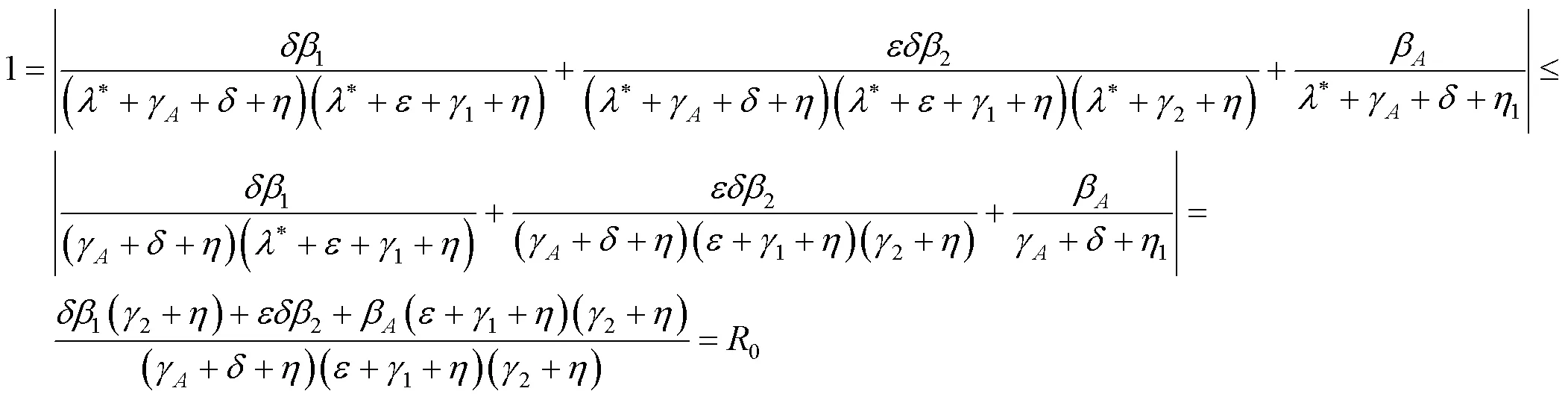
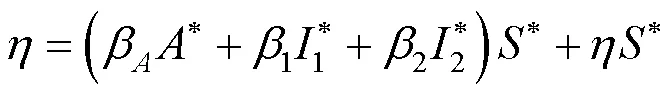
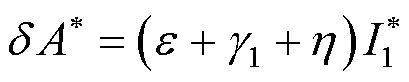
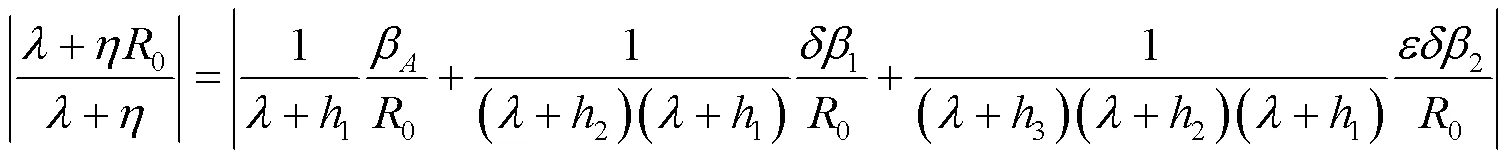
将式（5）～（8）代入式（2）中，可得

4　数值模拟

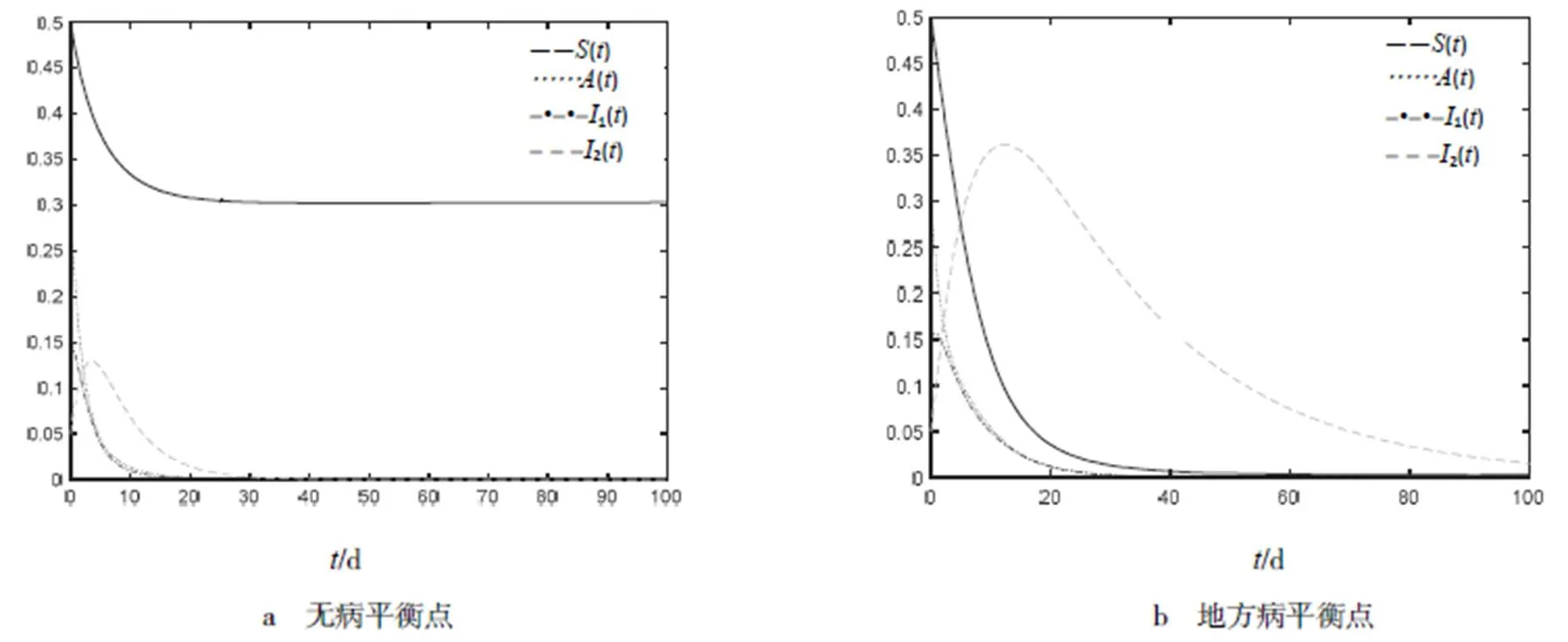
图2 无病平衡点和地方病平衡点的稳定性

由图2可以看出，数值模拟结果与定理3～4结论相符．

5　结语

[1] 杜金姬，秦闯亮，陈海波，等．一类具有病毒变异的随机SEIR传染病模型的灭绝性与平稳分布[J]．应用数学，2021，34（3）：768-778．

[2] 梁桂珍，方慧文，王伟杰．一类具有Logistic增长和病毒变异的SEIR传染病模型的稳定性分析[J]．河南科技学院学报（自然科学版），2021，49（2）：48-53．

[3] Shuai Z，Van den Driessche P．Global Stability of Infectious Disease Models Using Lyapunov Functions[J]．Siam Journal on Applied Mathematics，2013，73（4）：1513-1532．

[4] Sayampanathan A A，Heng C S，Pin P H，et al．Infectivity of Asymptomatic Versus Symptomatic COVID-19[J]．The Lancet （British edition），2021，397：93-94．

[5] 夏立标．一类传染病模型无病平衡点的全局稳定性[J]．浙江大学学报（理学版），2014，41（4）：391-398．

[6] Wendi W，Zhien M．Harmless Delays for Uniform Persistence[J]．Journal of mathematical analysis and applications，1991，158（1）：256-268．

[7] Haddad W M，Chellaboina V．Stability Theory for Nonnegative and Compartmental Dynamical Systems with Time Delay[J]．Systems & Control Letters，2004，51（5）：355-361．

[8] 高建忠，李志民．利用代数方法证明地方病平衡点的全局稳定性[J]．哈尔滨商业大学学报（自然科学版），2019，35（2）：234-236．

[9] Gao Jianzhong，Zhang T．Analysis on an SEIR Epidemic Model with Logistic Death Rate of Virus Mutation[J]．Journal of Mathematical Research with Applications，2019，39（3）：259-268．

[10] Van den Driessche P，Watmough J．Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission[J]．Mathematical Biosciences，2002，180（1）：29-48．

[11] Castillo-Chavez C，Feng Z，Huang W．On the Computation of Ro and its Role On Global Stability[J]．Mathematical Approaches for Emerging and Reemerging Infectious Diseases，2002，125：229-250．

Epidemic model with asymptomatic infection and virus mutation

FAN Jiaxin，SUN Fuqin

（School of Sciences，Tianjin University of Technology and Education，Tianjin 300222，China）

A class of epidemic model with asymptomatic infection and virus mutation was studied．The basic reproduction number of the model were calculated，the disease-free equilibrium point and endemic equilibrium point of the model were obtained．Then，the sign of the characteristic root of Jacobi matrix and the method of Lyapunov functions were used to analys the stability of the disease-free equilibrium point and endemic equilibrium point with different values of basic reproduction number．Finally，the obtained results were verified by numerical simulation．

asymptomatic infection；virus mutation；epidemic model；stability

1007-9831（2023）09-0009-07

O175.13

A

10.3969/j.issn.1007-9831.2023.09.003

2023-01-03

范佳欣（1998-），女，江西新余人，在读硕士研究生，从事生物数学研究．E-mail：fanjiaxin.1118@qq.com

孙福芹（1970-），男，山东单县人，教授，博士，从事偏微分方程及生物数学研究．E-mail：sfqwell@163.com