应用于CMOS图像传感器的高速全差分两步式ADC设计方法

郭仲杰 王杨乐 许睿明 刘绥阳

(西安理工大学 西安 710048)

1 引言

CMOS图像传感器(CMOS Image Sensor,CIS)由于其高集成度、低成本以及低功耗的优点，在人工视觉和航天领域等应用场景下，占据了大规模的市场并越来越不可替代。目前限制CIS曝光速度的处理都落在了读出信号处理部分，而模数转换器(Analog-to-Digital Converter, ADC)又是CIS读出电路的重要组成部分，是CIS性能提高的关键。近年来对于应用于CIS领域ADC的研究，涉及了大量不同的ADC拓扑结构，例如流水线型ADC[1]、循环型ADC[2]、σ-δ型ADC[3]、逐次逼近型ADC[4]、单斜式ADC(Single-Slope ADC, SS ADC)[5]以及基于上述ADC架构的各种组合等。但考虑到功耗、面积和速度的折中关系，并非每一种ADC架构都能在CIS中得到有效应用。

SS ADC主要由比较器、数字逻辑控制单元、计数器以及被所有列电路共享的斜坡信号发生器构成，相较于以上其他类型的ADC具有更好的面积和功耗优势，同时也相对容易地保证列之间的一致性，从而使列固定模式噪声(Fixed Pattern Noise,FPN)最小化，因此创新和发展出更快速的SS ADC架构已成为目前CIS领域主流的研究方向[6–10]。由于SS ADC特有的转换速率与转换精度之间呈指数型相关的量化方式，目前对SS ADC的研究，主要集中在如何在保证同等量化精度的前提下，创新出能打破速度瓶颈的量化模式。目前的前沿研究进展如串行两步式SS ADC，将整个量化过程分为在时间上串行的A bit粗量化与B bit细量化，将完成一次模数转换所需的2(A+B)个量化周期拆解为了2A和2B量化周期的和，节省了部分时间；全并行两步式SS ADC，将整个量化过程分为在时间上并行的A bit粗量化B bit与细量化，由于时间上的并行原理，完成一次模数转换将只需要MAX(2A,2B)个时钟周期；以时间数字转换(Time-to-Digital Conversion,TDC)技术为依托的SS ADC等，然而目前对于高帧频CIS的研究仍存在较大的瓶颈，在ADC研究进展仍有较大的速度提升空间[11–15]。

本文在传统两步式SS ADC的基础上，提出了一种应用于CIS的高速全差分两步式ADC结构，在保证SS ADC的功耗和面积优势的前提下，以将差动量化嵌套在两步式的思想，完成更高速量化。另外在ADC中引入基于电平编码的TDC技术，在ADC量化的最后一个时钟周期，以不牺牲动态功耗为前提，完成更高速的量化，从而实现高速的两步式量化过程。本文着重分析了该两步式ADC设计思想，并在实验平台进行了电路搭建和全面的参数测试。

2 CIS系统架构研究

CIS的整体架构如图1所示：包括尺寸规格M×N的像素单元、列偏置模块、行驱动模块、控制器、读出电路、时钟信号产生电路以及各个模块的信号驱动电路。其中像素单元完成光信号到电信号的转换过程，由读出电路将得到的电信号进行采样、放大、量化过程，时钟信号产生电路和控制器以及列偏置模块、行驱动模块为像素单元和读出电路提供时序控制和模拟偏置，共同完成图像的处理和读出[16–20]。

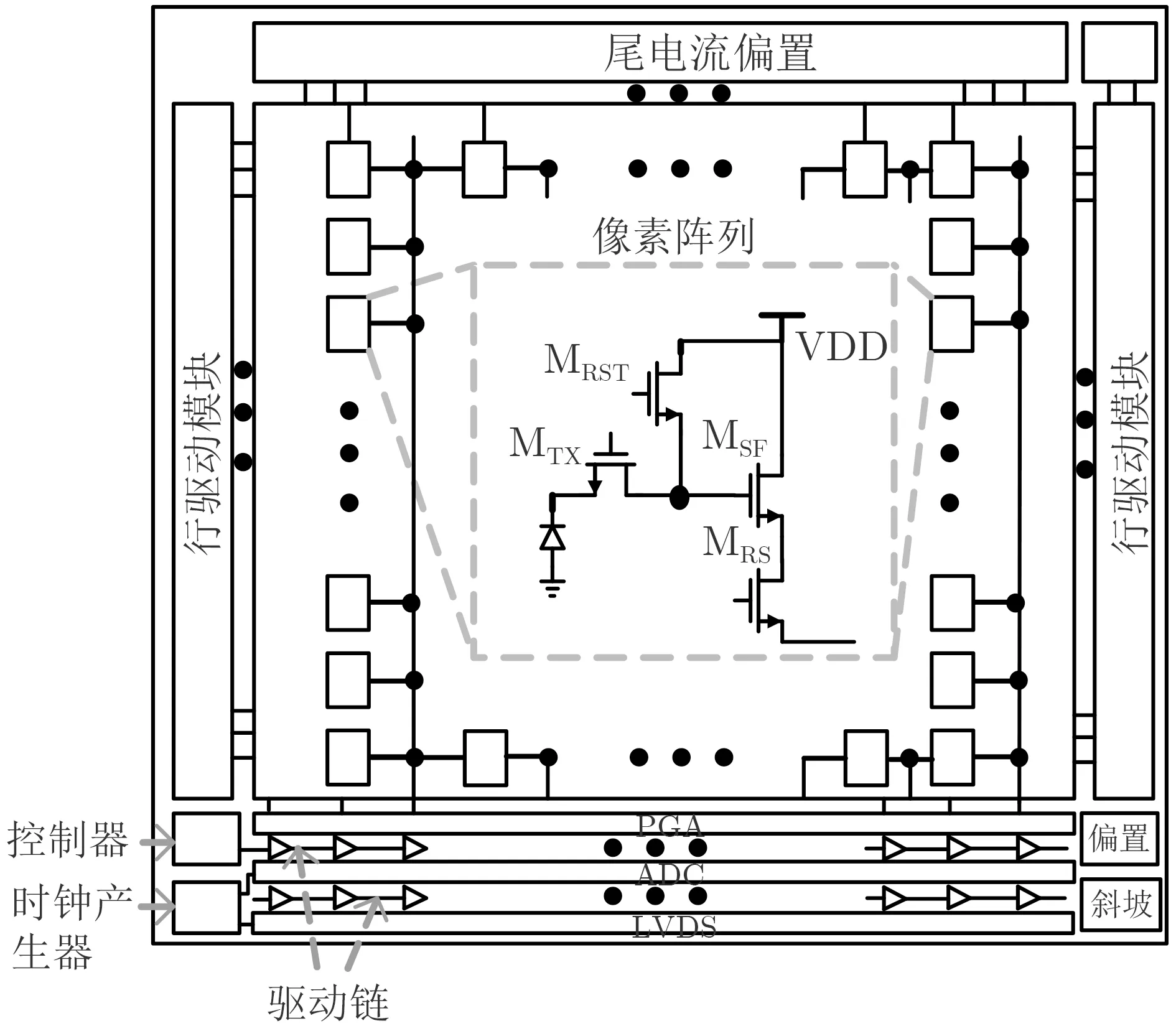
图1 CMOS图像传感器系统框架示意图

不论是目前CIS主流的全局曝光模式还是卷帘曝光模式，目前对曝光速度的限制均落在了电信号的读出量化阶段，而ADC又是约束信号量化处理的关键一环。因而为了保证较高的帧率，需要较高的ADC采样率；同时为了保证成像的质量，又必须保证较高的ADC精度[15,21–24]。因此在CIS的逐行读出下，列级ADC的转换时间则成为像素信号读出的最大限制，式(1)展示了帧频与列级ADC的转换时间的关系

其中，f为帧频，T为列级ADC量化一行所需要的时间，R为像素行数。

SS ADC系本身的量化方式，每提高1 bit的转换精度，其速度将以指数形式进行衰退，因此提升单斜式AD转换技术的核心主要集中在结构的优化创新，并且将会是CIS后续发展的一个突破方向。

3 高速全差分两步精度扩展式ADC设计思想

系SS ADC本身的量化速度存在的缺陷，目前对应用于大帧频CIS高速SS ADC研究历程由串行量化向并行量化方向的拓展，这种时间并行的思想，将是打破速度瓶颈的关键。而目前对于SS ADC并行量化的最新研究动态，其时间并行的效率并不显著，有且仅有33%[24]。而本文提出的全差分两步式设计思想，在时间上的并行利用率达到了50%，为高帧频CIS的实现提供了切实可行的理论基础和实现方案。

对于全差分两步式SS ADC的量化过程，总共分为两个步骤：(1) 模拟时间转换(Analog-to-Time Conversion, ATC)；(2) 时间数字转换。在本文全差分的电路架构中，该结构在整个动态范围下能识别的最小电压值是一个时钟周期内斜坡信号的变量。如果将斜坡比作一把标尺，斜坡上产生的变量就是这把标尺的分度值。因此，可以将斜坡信号等效为对斜坡信号增量或者减量求和产生的等效上升斜坡Vra1或等效下降斜坡Vra2。从ATC的角度分析，比较器会直接将输入信号在斜坡信号上时间关系映射出来，完成模拟信号到时间信号的转变。从TDC的角度分析，比较器之后的数字计数逻辑会把这段时间关系映射出来，完成时间信号到数字信号的转变。

图2为两步式SS ADC正常量化示意图，每个输入斜坡台阶值与数字计数逻辑一一对应，具体到M bit的粗量化而言，分为2M个粗台阶，每个粗台阶的量化时间对应一个时钟周期TCLK，所以完成粗量化需要的时间为

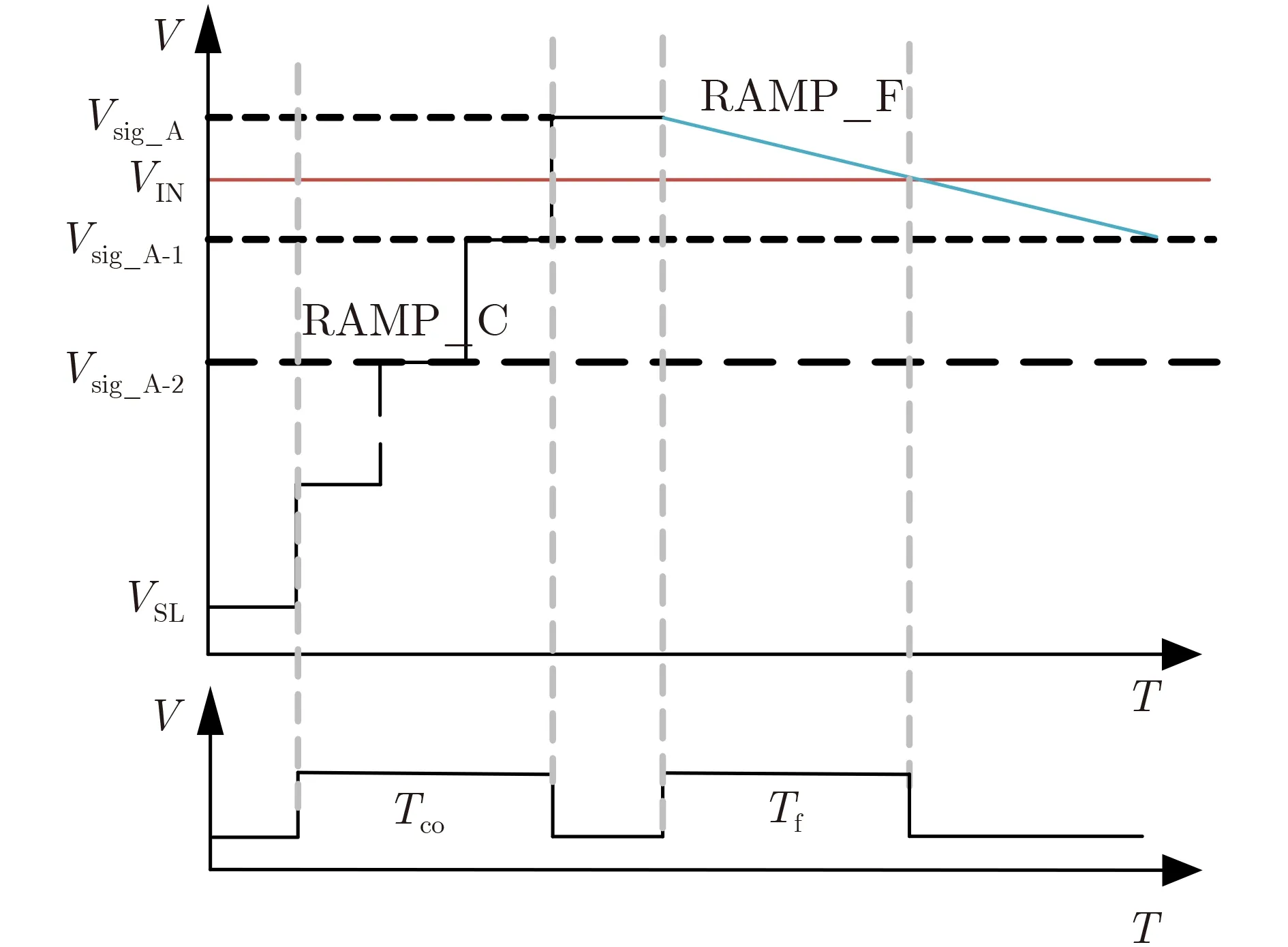
图2 两步式SS ADC量化示意图

由于差动粗斜坡的引入，每个粗台阶的量化时间仍然为TCLK，不同的是，粗量化的动态范围被一分为二，此时一半的粗量化时间变成了冗余时间，最终完成粗量化所需要的时间为

值得说明的是，对于细量化而言，必须使用在粗量化中触发的相同比较器。因此，细相位仅使用单比较器。这意味细量化将使用全斜坡摆动。就N bit细量化而言，RAMP_F被划分为2N个步长。 每个细量化步骤的转换时间对应于一个时钟周期TCLK，因此，完成细转换所需的时间为

考虑到一般情况，完成一次嵌套差动斜坡的两步式量化，假设有M bit的粗量化和N bit的细量化，最终完成一般两步式粗细量化所需要的时间为

本文将全差分的思想引入两步式SS ADC的实际量化中，在某种程度上类似于时间交织技术，将粗斜坡和细斜坡的量化时间作完全并行处理，由此进行时间共享，将串行的量化模式改进为并行量化模式，大大提高了时间利用率，达到高速量化的目的。由于SS ADC的转换时间依托转换精度是以指数倍衰减，所以这种量化机制在精度越高的情况下，速度收益越明显。这是本文对于速度提升做出的第一个创新。

本文提出的全差分两步式量化模式带来的有益效果是：(1) 形成了区别于串行量化的并行量化模式，同时由于差动斜坡的存在，保证了系统的一致性和鲁棒性。(2) 相较于传统两步式SS ADC该结构带来50%以上的速度收益，且这种速度收益在越高精度量化过程中越明显。

4 低功耗电平编码TDC设计方法

如图3所示，两个待转换的模拟信号A和B展示了一种边界量化情况，在分辨率的制约下，输入信号A和B之间形成了具有相同数字输出的模拟信号区间：若待测信号大于待转换模拟电压B，则ADC的数字输出会增加一个单位；若待测信号小于待转换模拟电压A，则ADC的数字输出会减少一个单位；当待测信号处于AB的信号区间内，要想得到更高精度的量化结果，一种方法是全局范围内采用更高频率的时钟以此缩短ADC的单次量化时间范围；另一种方法是在局部使用更精确的量化，即在信号所在的时钟周期内，利用更高精度的时间数字转换器量化该信号与Time2的时间差值，即TDC。由于在ATC时利用了比较器判别了输入信号在斜坡信号上的时间尺度，在TDC时又利用更高精度的时间数字转换器衡量了比较器翻转时刻与当前时钟周期结束时刻的时间尺度，最终得到的时间信号都将通过数字计数逻辑整合得到理想的数字码。在此基础上，就需要着重考虑ATC与TDC的匹配性问题[15,25,26]。

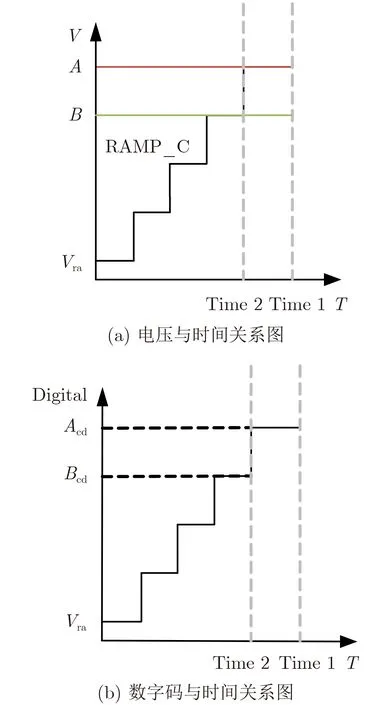
图3 时间差值量化示意图

传统TDC的编码方式如图4所示。在这种编码逻辑下，随着4相时钟的依次到来，时钟对应的4个触发器依次触发，在CLK1～CLK4时钟沿到来的不同时刻，触发器的输出对应一一翻转，从而通过这种沿触发的方式，产生不同的输出结果，再通过编码器对不同的输出结果进行编码，得到00～11的2 bit二进制数字转换结果。

图4 传统时钟压缩型TDC编码原理示意图

这种技术的TDC通过D触发器特有的沿触发方式来进行编码，若要完成2 bit的时间数字转换功能需要延迟锁相环(Delay phase-Locked Loop,DLL)配备严格的4相时钟，由于DLL的压控延迟链需要通过反馈的方式来产生稳定且具有相关性的4相时钟，但是由于非理想因素会导致的时钟抖动问题，在四相时钟下会表现的更加明显且不可控[27]。这种模式下的TDC会使得ADC量化的精度和速度都大幅度下降，实际转换效果并不理想。

本文提出的电平编码原理如图5所示。由DLL提供两项时钟CLK1和CLK2，利用这两项时钟的相位差，在一个时钟周期内的不同量化时刻，CLK1和CLK2对应有不同的高低电平组合，再通过D触发器和基本逻辑门组成的电平编码电路进行编码，在1个时钟周期内，输出00～11的2 bit二进制数字转换结果Y0和Y1。

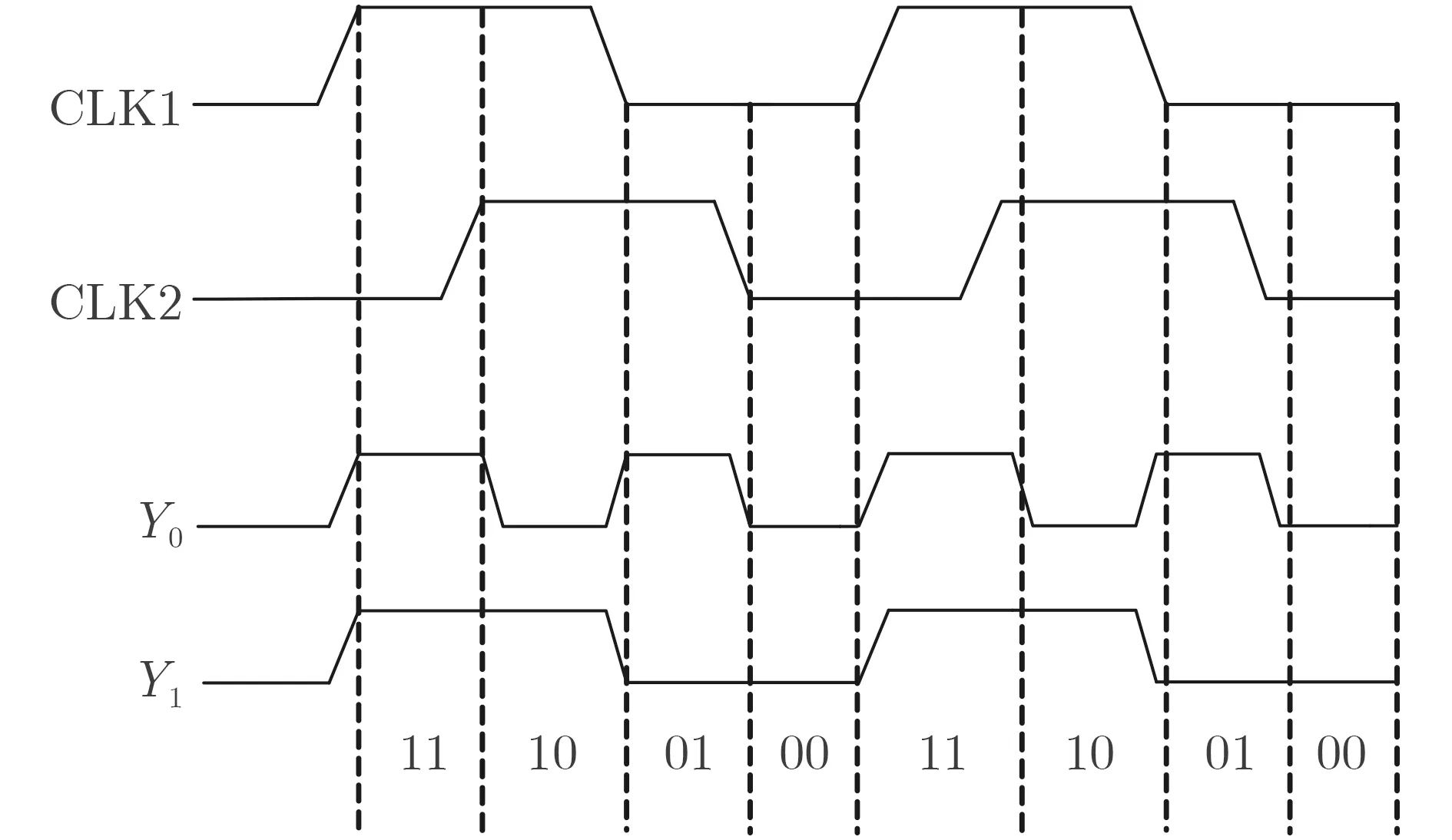
图5 本文TDC电平编码原理示意图

通过TDC的编码器将延DLL产生的多相时钟信号进行编码后，再通过D触发器(由于是沿触发的特性)，将比较器的翻转判定时间同时作为TDC的START信号，最后将2 bit TDC输出的00～11的低2位数字码与计数器数字码进行整合，将ATC和TDC完成最终的匹配。

由于差动斜坡架构并不能将时间的利用率提高到极致，基于以上的工作，不难发现，SS ADC的转换时间还受到时钟频率的影响，在ADC的数字逻辑模块，做有计数器模块，是通过时钟沿触发来进行计数的。这并不能说时钟频率越快越好，因为系ADC的模拟电路部分，ADC对高频时钟的耐受度也会有限制，A/D转换的最后一位数字码的读出靠时钟沿来控制，这也就是说，在比较器完成输入信号与斜坡信号判决之后，并不能马上完成数字码的输出，还需要等待下一个时钟沿的到来。因此，本文将利用这段时间差，将TDC技术插入于ADC中，进一步提高时间的利用率，在与两步式ADC相同的量化精度下，TDC将完成更高精度的模拟值逼近，本文设计了2 bit的TDC精度，将速度提升对时间的指数衰减降低2 bit，所以这也是本文对于速度提升做出的第2个创新。

基于单斜式与电平编码TDC电路结构示意图如图6所示，该电路带来的有益效果如下：

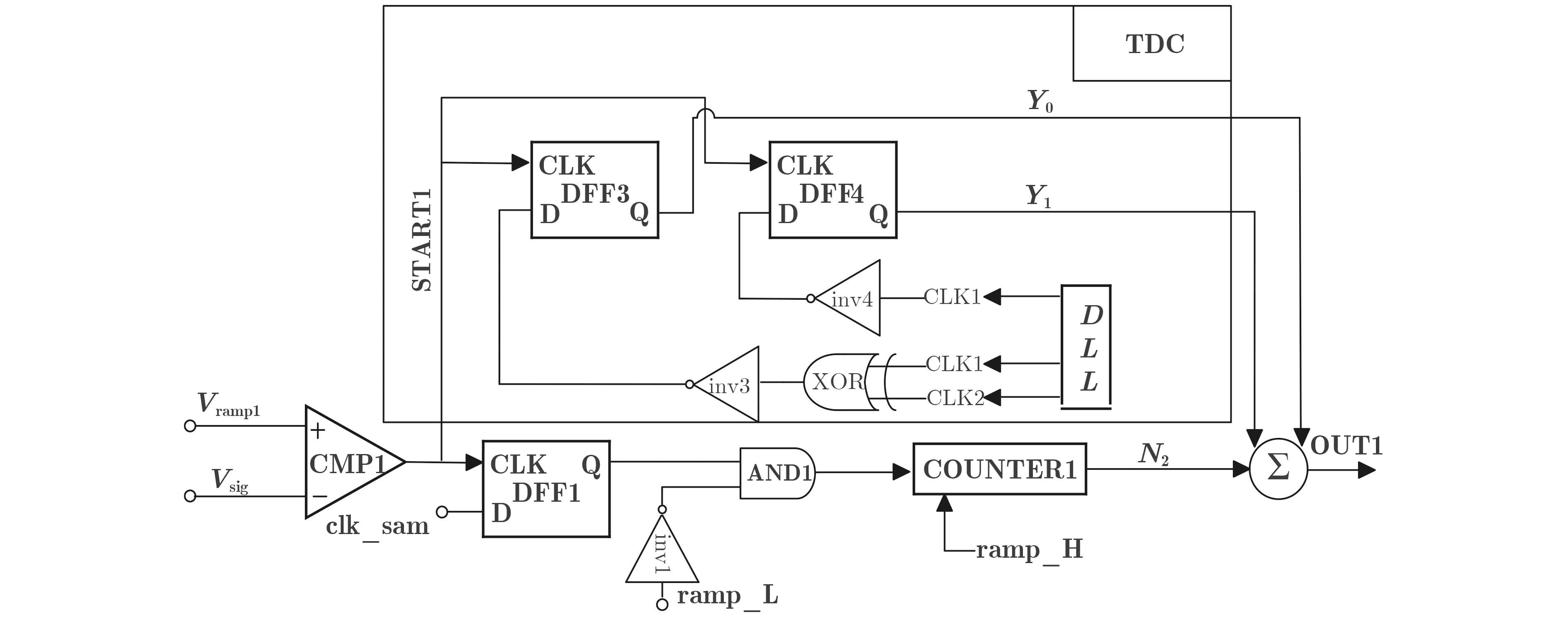
图6 基于单斜式与电平编码TDC电路结构示意图

(1)该结构只需要DLL提供两项时钟，利用两项时钟的电平进行数字编码，在这种编码方式下，更有效地释放了TDC对DLL的需求，同时改善了DLL的时钟抖动造成量化精度不高的问题。

(2)传统的沿编码需要复杂的编码逻辑，而本文提出的TDC结构编码方式较为简单，这种简单的编码结构降低了ADC数字模块的动态功耗，这在大面阵CIS的应用中显得尤为显著。

(3)待转换信号输入到达输出的延迟更小，量化速度更快。可以在保证量化精度的同时，完成时间-数字的高速转换过程，为打破SS ADC的速度瓶颈提供了有效的解决方案。

5 12 bit模数转换器详细设计

本文将全差分的并行量化思想与以电平编码为依托的TDC技术相结合，提出了高速全差分两步式SS ADC。如图7所示，将12 bit模数转换的量化过程拆解为了5 bit粗量化、5 bit细量化以及2 bit TDC量化过程。

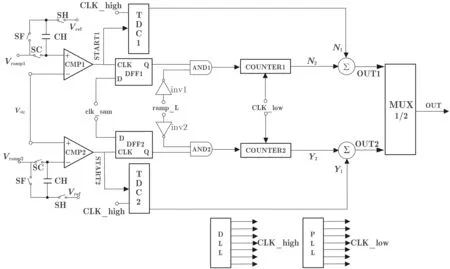
图7 基于差动斜坡与TDC的ADC结构示意图

该电路由全差分形式的采样电路、比较器、TDC以及数字计数逻辑组成，最终由数据选择器来完成转换结果的输出。其中数字计数逻辑所采用的低频时钟由锁相环(Phase-Locked Loop, PLL)提供，TDC所采用的等效高频时钟由DLL提供。斜坡发生器产生差分形式的斜坡信号Vra1和Vra2以及光电转换信号Vsig从采样电路完成系统输入。本文实现差动斜坡并行的架构，“差动”的思想也是模拟设计很重要的一环，对于差动的电路设计，在对匹配性方面可以做到更好，这在CMOS图像传感器中，无论是版图匹配性还是ADC的稳定性方面，都能得到更好的体现。

先进行粗量化，在开关电容控制电路中，控制开关SC和SH为导通状态，此时Vra1和Vra2为差动形式的粗斜坡电压，从初始值开始，步进到粗斜坡电压的满摆幅电压VFS，每一次的步进值为粗斜坡电压的一个台阶值ΔC。比较器对斜坡输入信号和待量化信号Vsig进行比较，粗斜坡电压每步进增加ΔC，比较器便会比较1次，若经过m次步进，比较器的输出变为高电平，则表明输入信号为

在这个粗量化区间内，就找到了Vsig所在的粗量化区间，此时关断开关SH，电容CH就存储了此时的粗斜坡电压值(m+1)ΔC，电容CH的上下极板电压差为(m+1)ΔC–Vref，Vref为一固定电平。粗斜坡电压步进到满摆幅电压VFS之后，开关SC关断，粗量化过程结束。

然后进行细量化操作，此时在开关电容电路中，开关SF为导通状态，Vra1和Vra2此时为差动形式的细斜坡电压，定义为VR，接到开关电容电路中电容CH的下极板，由于电容CH存储了之前的粗斜坡电压值(m+1)ΔC，则比较器的斜坡输入端电压值VC为VR+(m+1)ΔC，细斜坡电压VR从–ΔC步进变化到Vref，每一次的步进值为细斜坡电压的一个台阶值ΔF。VC就从mΔC变化到(m+1)ΔC，即对VIN所在的粗量化区间进行细量化。比较器对VC和待量化信号Vsig进行比较，若细斜坡电压VR经过n次步进，比较器的输出变为高电平，则表明输入信号为

最后进行2 bit的TDC过程，细量化的结束信号作为TDC的开始信号，此时的细斜坡计数器的低频时钟的时钟沿作为TDC的结束信号，通过周期性的编码过程，完成可配置在SS ADC中的可循环式的编码，TDC编码所需要的等效高频时钟由DLL提供。同时为了具备较强的调整空间，计数器采用简单的链式结构，底层触发器采取同步可复位及置位的D触发器，设计复位权重高于置位，配合与非门电路实现初值可配的计数器设计。紧接着，通过将初值置为–1，将省去细量化计数结果减去TDC计数结果这一过程，而实际的计数变为了粗细量化的计数结果作为高10 bit位数字码，而将TDC的反码直接作为低2 bit位数字码，直接完成12 bit的模数转换结果，使得列级ADC电路省去了减法器电路的面积和功耗开销。

最终，在这个细量化区间内，1个完整的量化周期结束。

对于本文的并行量化模式，类似时间交织的形式，对于粗量化而言，差动双斜坡在时间上同步进行，比较器CMP1和CMP2同时开始工作，通过时序的整合，在两步式的基础上，将时间的利用率提高了50%，在SS ADC本身速度与精度呈现指数衰减的情况下，将并行引入在两步式的量化过程中，所以并行模式才是本文设计的核心思想之一。

基于差动斜坡与TDC的ADC电路工作时序如图8所示，回归一般情况，差动斜坡为M bit粗斜坡与N bit细斜坡组成，TDC为Q bit，在保证总的量化精度为(M+N+Q) bit的前提下，最终的实际量化时间仅为2M–1+2N，相较于上述传统两步式ADC而言，可以完成更高速的量化，为高帧频大面阵的CMOS图像传感器实现提供了有效的解决方案。

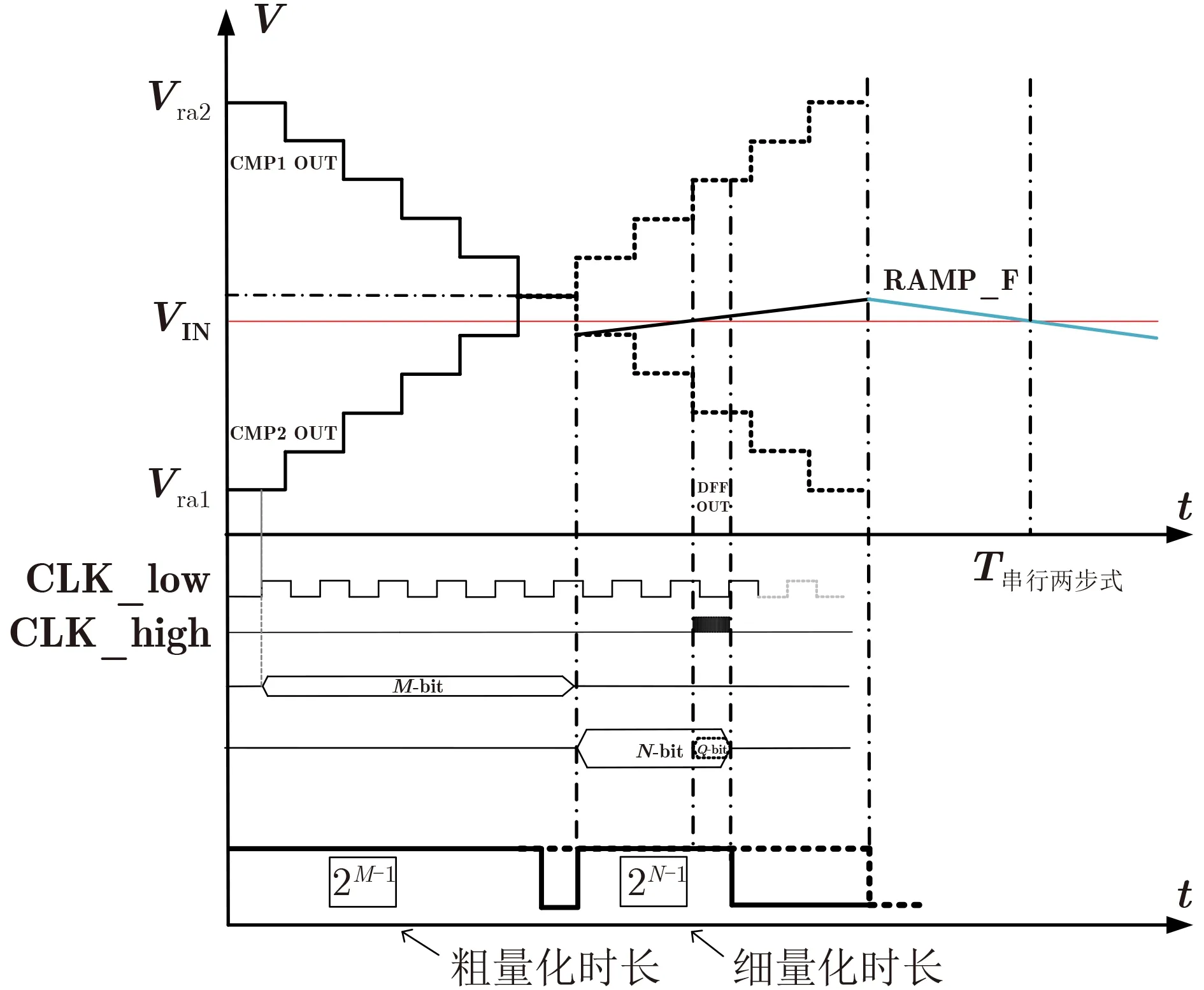
图8 基于差动斜坡与TDC的ADC电路工作时序图

6 验证结果与数据分析

本文基于55 nm 1P4M CMOS工艺，完成了基于差动斜坡与TDC技术的高速全差分两步式ADC的具体电路设计与物理版图实现，并成功应用于一款6 400万像素的读出电路芯片，如图9所示为全芯片的实际照片。其中，ADC量化精度为12 bit，模拟和数字电源分别为3.3 V和1.2 V，时钟信号频率100 MHz。为了充分验证本文所提方法的先进性和可行性，本次设计面向8 192×8 192规模的CMOS图像传感器的验证平台进行了性能参数测试和数据分析。

模拟和数字单元组成的各功能电路拼接得到的列复用单元如图10所示，模拟模块与数字模块采用组格式分别向各单元供电，在纵向空隙设置了大量FD电容保证电源对数字噪声的抵抗能力，数字电路与模拟电路采用分离设计与独立衬底的设计方式，避免数字噪声的串扰。

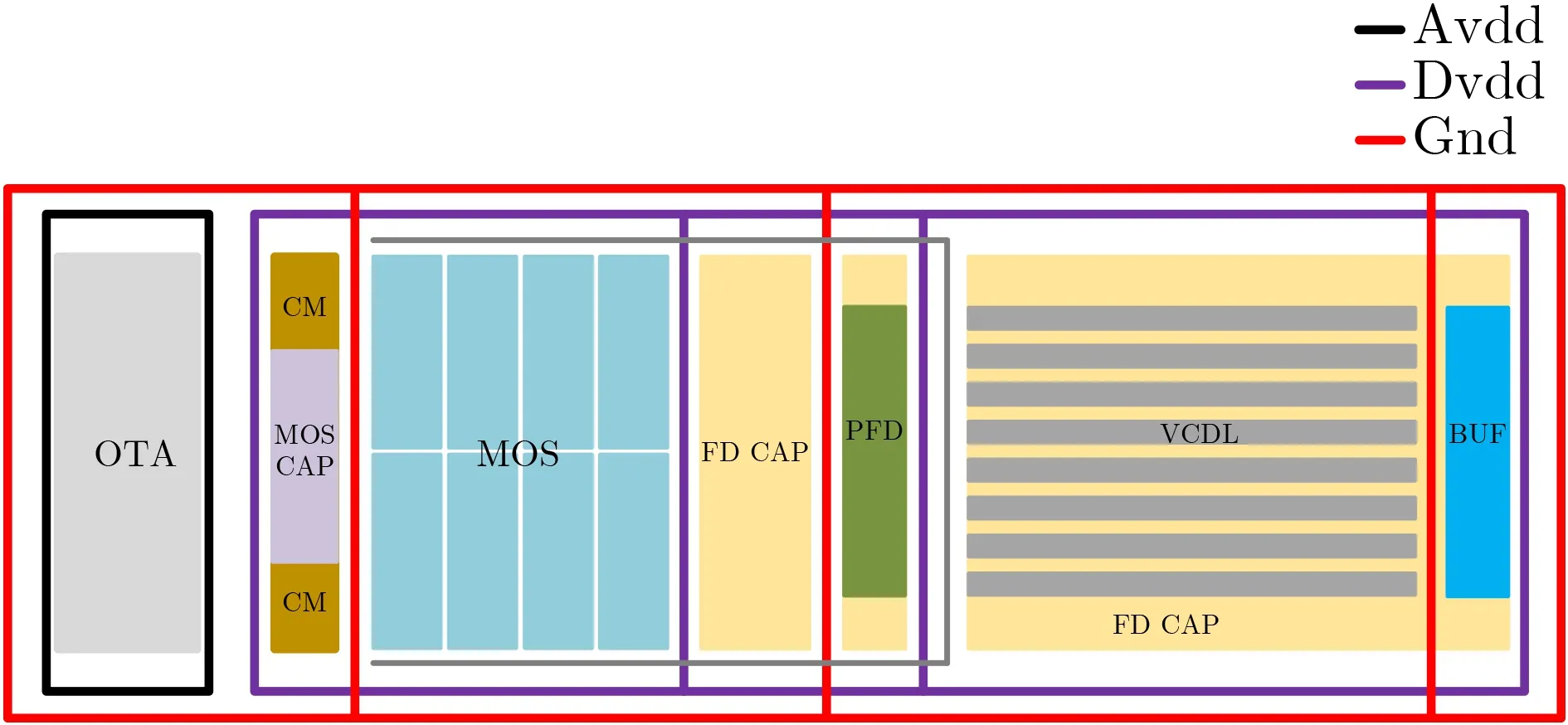
图10 ADC整体版图设计

考虑到实际应用情况，本文版图的设计面向8 192列大面阵CIS的应用。由于复用的设计特性，其信号传输路径与接口信息均与复用单元保持一致。模拟偏置信号经由预留的布线通道向面阵内所有列电路提供偏置，除电流偏置采用每个复用单元独立设置的方式外，其余模拟信号均由列电路共用。电流偏置通道与模拟信号通道采用分离设计，利用8 192路电路线独立的向每一个复用单元提供偏置。所有数字信号通过复用单元内设计的驱动单元构成面阵级驱动链，向所有列电路提供控制信号。信号在驱动链内的延迟约为10 ps，远小于系统时钟周期。由于TDC所需的2相时钟在阵列传递中与时钟信号具有相似的传递路径，依然能保证TDC过程中利用多相时钟对固定时钟周期的区间划分。且ADC的每一功能电路均受到时钟信号的约束。因此在8 192级规模的信号延迟下。ADC阵列的任一列的控制信号均具有对时钟信号的一致性。基于该设计原理下的ADC阵列，对于控制信号的延迟具有较高的宽容性。由于复用的设计特性，1 024阵列的各项性能均与列复用单元存在一致性，ADC整体版图如图11。

图11 ADC整体版图

图12和图13为本实验静态仿真测试结果，以0.2LSB观测精度进行测试，得到的微分非线性(Differential NonLinearity, DNL)如图12所示；积分非线性(Integral NonLinearity, INL)如图13所示：DNL为+0.6/–0.6, INL为+1.2/–1.4。

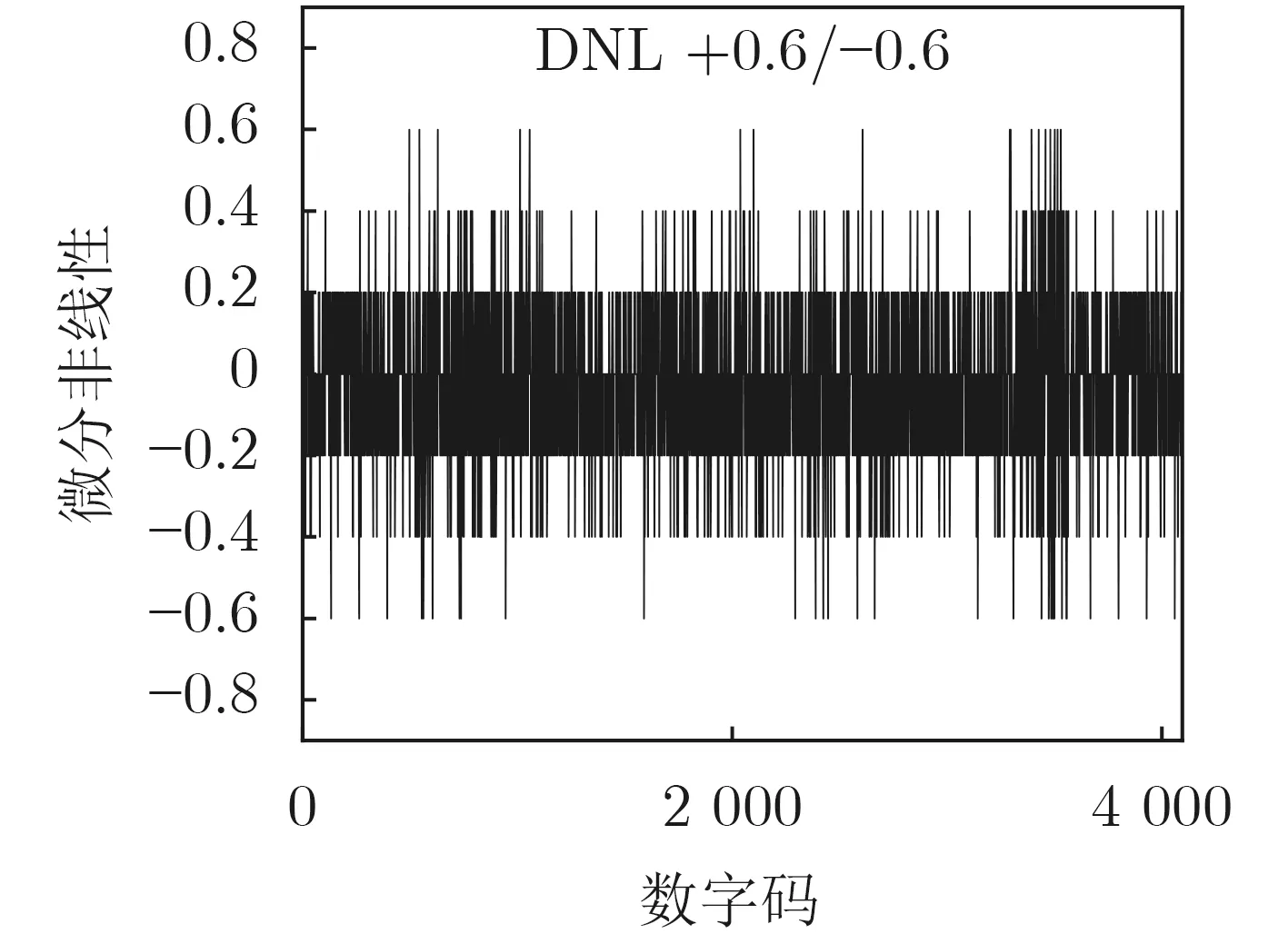
图12 微分非线性(DNL)测试结果

图13 积分非线性(INL)测试结果

以1.21 MHz的采样频率对147.964 Hz信号采样8 192组数据进行FFT分析结果如图14所示。本文设计的ADC信噪失真比(Signal Noise Distortion Ratio, SNDR)为70.08 dB，有效位数(Effective Number Of Bits, ENOB)为11.35 bit，列级功耗为62 μW，动态范围为1.6 V。

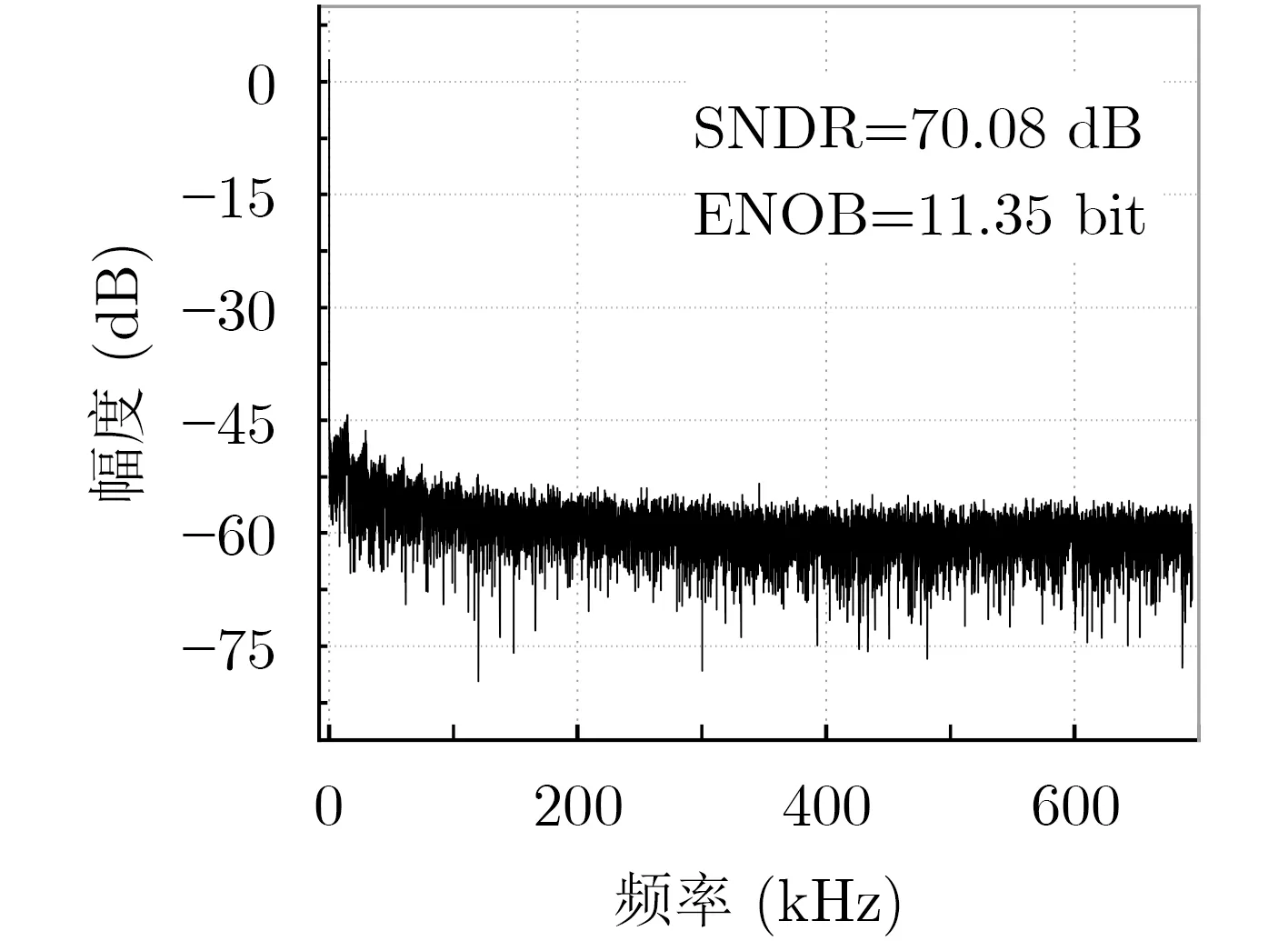
图14 信噪比分析

表1为本文设计方法与目前同领域前沿研究对比结果，表中ADC架构均在12 bit的精度下进行对比，文献[22–24]均为粗细斜坡量化的两步式结构，与文献[22]相比，本文功耗减少了14%，转换速度缩短了95.2%；与文献[23]相比，本文功耗减少了45%，转换速度缩短了92.5%；与文献[24]相比，本文功耗高出32%，但是带来了将近62.5%的速度收益，而且静态特性更好；文献[1]是以SS ADC与TDC相结合的两步式架构，相较于文献[1]，本文功耗减少了65%，转换速度缩短了52%。以上的对比可以看出，在相同精度下，本文设计的ADC与目前前沿架构相比，在保证功耗的前提下，依然具有明显的速度优势，转换速度提高了52%以上。本文设计的ADC由于工艺和系统架构的先进性，实际带来的速度提升效果与理论分析基本一致。综上所述，本文提出的设计方法与现有的参考文献相比，具有明显的优势。

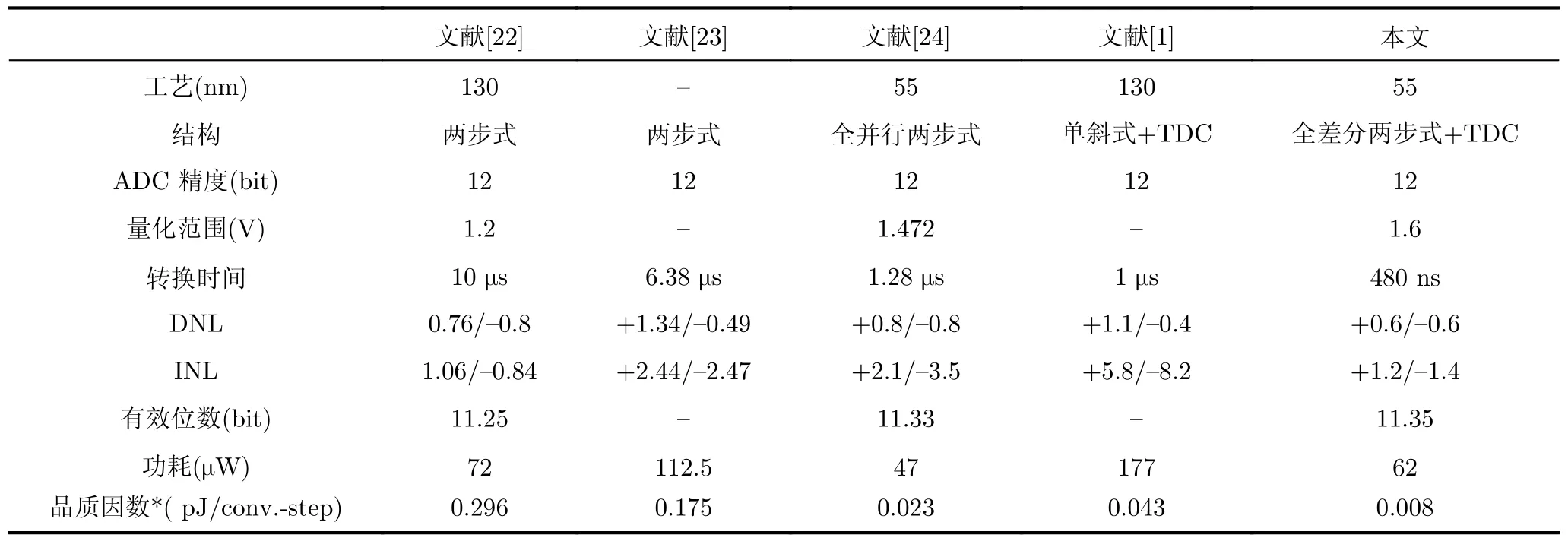
表1 本文设计方法与文献的对比结果

7 结论

本文针对高帧频CMOS图像传感器对列级处理电路的高速要求，提出一种基于全差分两步式ADC和低功耗TDC相结合的高速高精度ADC设计方法，该ADC设计方法将差动量化嵌套在两步式的量化中，形成了区别于串行量化的并行量化模式，同时由于差动斜坡的存在，保证了系统的鲁棒性；针对传统TDC技术与单斜式ADC的匹配性问题，提出了一种基于电平编码的TDC技术，在ADC量化的最后一个时钟周期完成时间数字转换，实现另一个层面的两步式量化过程。最后在一款基于55 nm 1P4M工艺的8 192×8 192规模CIS芯片上进行了具体电路设计验证，实验结果表明，该ADC在单次量化达到480 ns的同时，将DNL的峰值误差控制在了+0.6/–0.6 LSB，将INL控制在了+1.2/–1.4 LSB，并且对ADC的转换结果进行FFT分析可得到包含输入信号在内的幅频曲线，将ADC的系统噪声和随机噪声考虑在内，SNDR达到了70.08 dB，有效位数达到11.35 dB。

可见，本文提出的设计方法将现有SS ADC的转换速度提高了52%以上，且随着精度的提高对时间的收益越明显，因此，该设计方法为高帧频大面阵CMOS图像传感器提供了先进的实现方案。