基于机器视觉的便携式坐标测量系统

康 新 刘 佳 王文涛 孙凤鸣

1.中国民航大学中欧航空工程师学院 天津 300300;2.锐迪科微电子科技(天津)有限公司 天津 300300;3.上海飞机设计研究院 上海 201210

随着机器视觉技术的飞速发展,机器视觉技术逐渐被应用于工业生产的检测环节。以光学靶标式测量系统为代表的视觉测量系统在复杂三维场景的测量中逐步得到应用,特别适用于测量异形结构的孔间距、有间隔的几何尺寸等复杂结构,在某些场合下相对于不便移动的三坐标测量机具有一定的优势[1]。国外相关机构对该项技术进行了深入研究,并开始应用在汽车和飞机等先进制造领域。目前,国外的相关产品价格昂贵,而国内受限于技术水平尚未取得突破性进展。因此,本文深入研究光学标靶式测量系统的核心技术,从而设计出一套测量较为准确的光学靶标式测量系统。

1 硬件系统设计

本文中的光学靶标式测量系统由光学靶标、相机以及计算机这三部分构成。光学靶标主要由主体、测头探针以及二者的连接部分所组成,用于定位样品待测部位。双目视觉相机用于采集光学靶标上的特征点,计算机用于解算光学靶标上探针与样品接触部位的空间坐标。光学靶标整体系统如图1所示。

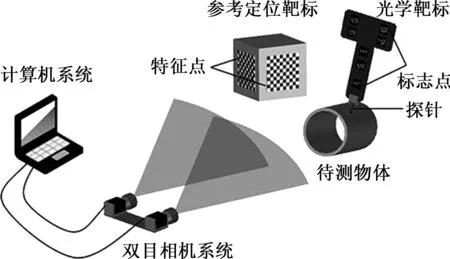
图1 光学靶标系统图

1.1 光学靶标设计

光学靶标在标定和使用过程中被认为是一个理想的刚体结构。我们假定靶标上各标志点间、标志点与测头探针间的相对位置恒定不变,则选择较高刚度、较小热膨胀系数和密度较小的碳纤维板材作为靶标的主体材料。测头探针既要保证工作在弹性范围内,又要达到一定的刚度。综合考虑后,测头探针的头部采用红宝石球形探针,通过碳纤维杆与光学靶标固连。

1.2 回光反射标志选择与设计

光学靶标上的标志点的中心坐标提取,对测量精度有较大影响。目前多为发光标志点,可以在光照度较小时进行工作,但对其中心坐标提取算法有较高要求。本文采用圆形回光反射编码标志点,其光照适应度较弱,但是中心提取算法精度较高和特征点匹配准确的特点,可以适用于室内测量场合。中心圆点周围的编码环10等分,每一个等分区域根据是否填充反光材料而形成不同的亮度区域,而得到逆时针顺序的10位二进制编码,具有编码的特点更利于其后续视觉检测方法中的特征点匹配。

2 标志点定位与空间坐标解算

2.1 利用椭圆拟合法提取标志点中心坐标

标志点经相机投影一般呈现椭圆特征。本文采用椭圆拟合法[2]提取标志点的椭圆特征中心坐标,分为两个步骤:首先,识别并提取椭圆或圆边缘像素点。边缘是指图像中局部灰度值呈现阶梯变化或屋顶变化的像素的合集[3],常用的边缘检测算子有Roberts算子、Sobel算子和Canny算子等。其次,通过对边缘像素点进行椭圆拟合获得椭圆的中心坐标。利用图像边缘检测算法获得边缘像素点的集合后,根据最小二乘椭圆拟合,确定椭圆特征的中心坐标。平面椭圆的一般方程如下:

Ax2+Bxy+Cy2+Dx+Ey+F=0

(1)

可将上述方程进行线性简化为最小二乘问题。

LX=[x2xyy2xy1]
X=[ABCDEF]T

(2)

将组成的椭圆轮廓的N个边缘像素点坐标代入上式,可以得到该椭圆轮廓的线性方程组,将‖X‖2=1作为约束条件引入,转化为最优化问题如下:

minLNX2s.t.X2=1

(3)

通过高斯—牛顿法等迭代方法可以求解式(3)获得椭圆系数X的最优解[4]。根据最优解,再通过如下的椭圆中心计算公式,便可以求得椭圆或圆的图像中心坐标。

(4)

2.2 解算空间点的三维坐标

利用双目相机解算光学靶标上的回光反射式编码标志中心坐标,并对编码环进行解码获得码值。通过码值可完成左右图像中对应标志点的匹配,进而利用双目立体视觉原理解算出标志点在相机坐标系下的空间三维坐标。

2.3 转站测量方法

当相机站位发生改变后,势必造成转站前后测量空间坐标系的割裂,因此需要一个参照物体,通过在不同站位提取特征进行匹配,建立起相机站位间的相对位姿关系,实现各测量站位到参考站位的统一。本文设计的参考定位靶标便是起到这一作用,基于参考定位靶标的相机转站测量原理如图2所示。

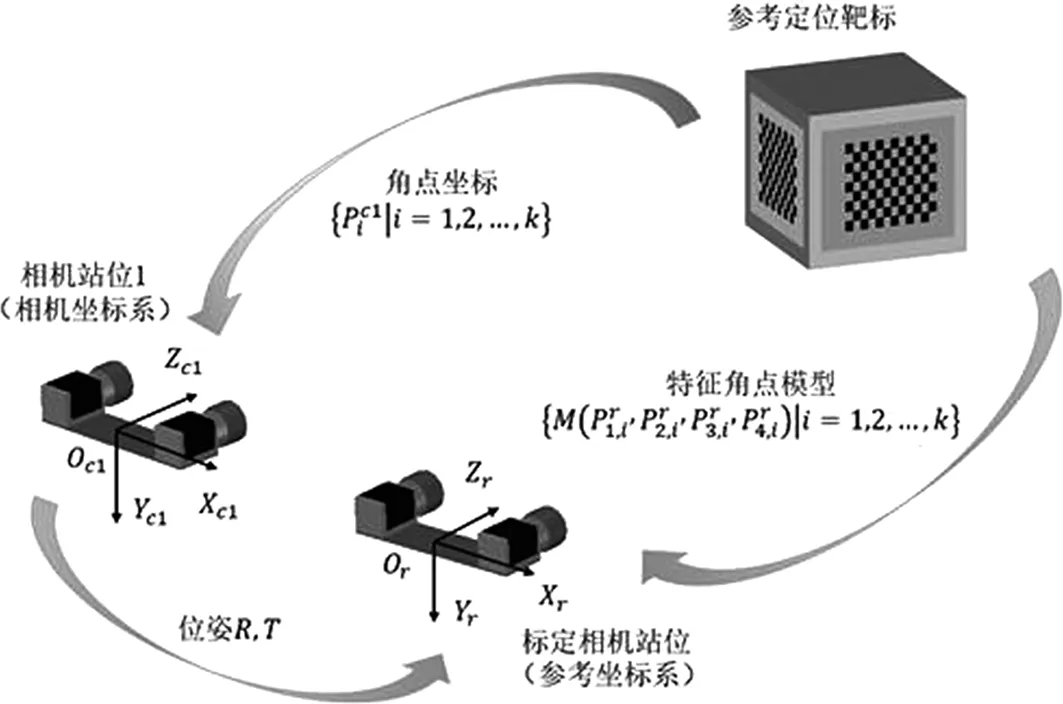
图2 基于参考定位靶标的相机转站测量原理

当完成了第一个相机站位下测量区域内的测量工作后,将参考定位靶标置于当前相机站位的视场内,通过双目立体视觉原理对靶标上第j个棋盘格角点进行测量,获得当前站位Oc1-Xc1Yc1Zc1下的棋盘格角点坐标:

(5)

通过奇异值分解法,可以解算出相机坐标系到参考坐标系的旋转矩阵Rc1r与平移向量Tc1r。通过求得的姿态关系,便可以将相机站位1下的测量结果变换到参考坐标系中。

为了测量站位1无法观察到的测量区域,在保证参考定位靶标始终在相机视场内的情况下移动至站位2,设该站位下相机坐标系为Oc2-Xc2Yc2Zc2,通过双目立体视觉原理测量棋盘格的角点坐标:

(6)

与站位1同理,可以解算出站位2相机坐标系到参考坐标系的旋转矩阵Rc2r与平移向量Tc2r,将相机站位2下的测量结果变换至参考坐标系中。无论相机站位如何,均可以将测量结果变换至参考坐标系,实现测量点坐标的统一。

3 系统标定和测量实验

3.1 相机标定实验

本文首先采用张氏棋盘格标定法[5]分别对左右相机进行单目标定,得到左右两个相机的内外参数,将其作为相机的初次标定结果。其次,根据相机的初次标定结果,以组为单位,分别计算左、右相机图片中棋盘格角点的重投影误差均值。再次,从采集到的40组匹配图像中,挑选20组重投影误差最小的图片。最后,利用这20组图片重新对双目相机进行标定,得到更为准确的相机内外参数。

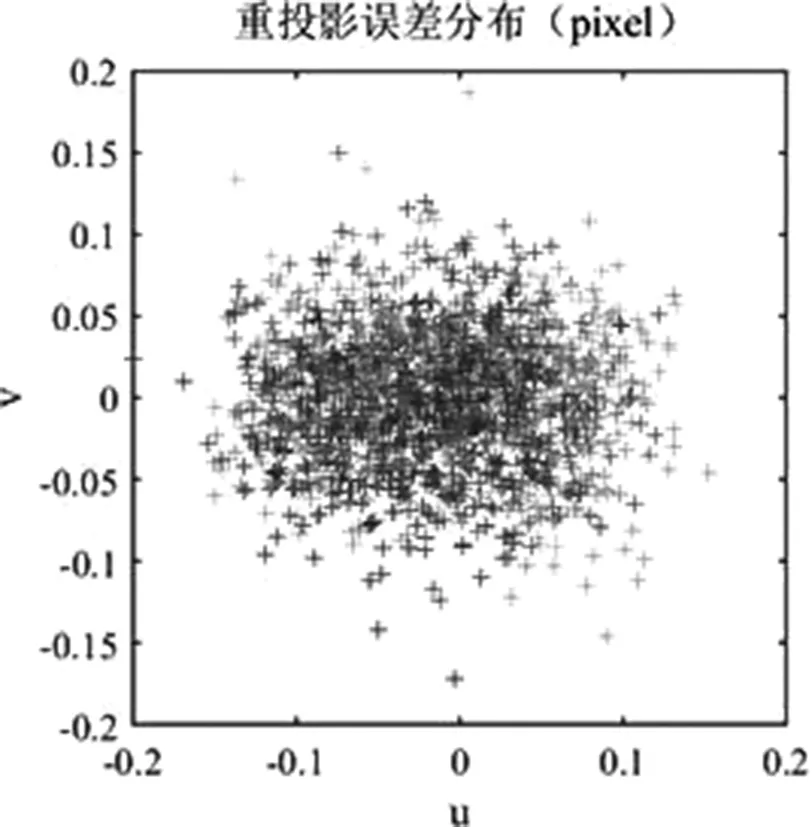
结果表明,二次标定可以通过摒弃成像质量较差的图片获得更加稳定的标定结果。图3为每个棋盘格角点重投影误差分布图,结果较为稳定。

3.2 光学靶标联合标定实验

本文采用的光学靶标联合标定方法将同时进行标志点自标定和探针测头中心位置标定,通过探针测头中心位置标定的图像可实现回光标志点自标定。

首先,采集测头探针中心的标定图像,将光学靶标的球形探针置于位置固定的锥孔中,旋转倾斜靶标,使用双目相机获得不同姿态下的15组靶标图像。其次,进行标志点自标定,使用椭圆拟合法获取每对图像中标志点中心的图像坐标。再次,对15组标志点的图像进行码值匹配获得15组标志点坐标集,其中每组坐标集包含7个回光标志点的空间三维坐标。最后,计算每组坐标集的重投影误差,选择重投影误差均值最小的坐标集作为光学靶标标志点自标定的结果。标志点空间三维坐标如表1所示。

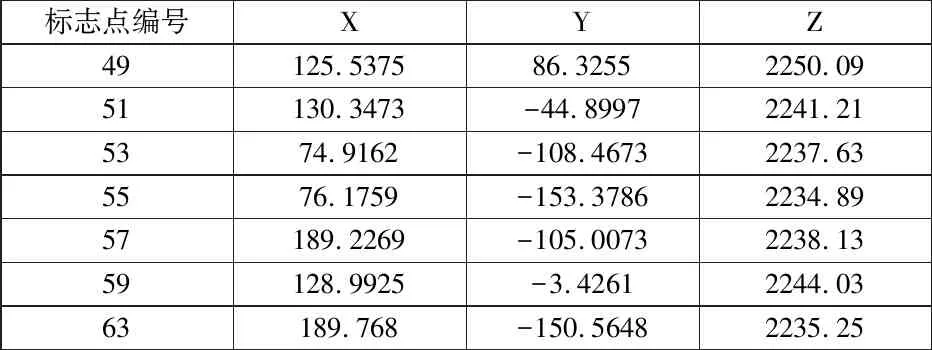
表1 光学靶标坐标系下标志点空间三维坐标(mm)

然后,根据坐标集建立方程组,求解探针测头中心的空间坐标。每一个标志点在不同靶标姿态下的空间坐标可以解算出一个探针测头中心坐标,7个标志点共可以解算出7个探针测头中心坐标,取均值作为探针测头标定结果。重复进行上述实验,结果如表2所示。

表2 探针测头中心位置标定结果(mm)

3.3 平面测量实验

可以通过平面测量实验来验证本文方法的有效性。首先,将测头探针与标准平面充分接触,均匀移动靶标并拍摄多张不同姿态的靶标图像。根据上文方法来获得各个靶标姿态下的测头球形探针中心坐标,作为标准平面采样点数据。然后根据测量得到的采样点数据,通过最小二乘评定法拟合最小二乘平面。平面的一般方程如下:

p=au+bv+c

(7)

根据采样点数据,进行平面拟合,目标函数定义为:

(8)

最小化目标函数,满足条件:

(9)

展开并化简得出矩阵形式的方程组如下所示:

(10)

根据上式求出对应的平面系数,并以最小二乘平面作为评定基准面,以平行于最小二乘平面,且具有最小欧式距离的两包容平面间的距离作为平面度误差值。采样点到最小二乘平面的距离公式如下:

(11)

由此平面度误差的最小二乘评定法结果为:

σ=max(di)-min(di)

(12)

根据上面的方法,对机加工制作的标定辅件上的平面进行采样测量,并拟合平面参数得到拟合后的平面方程为:

p=3.8603u-421.6624v+81935.9099

(13)

采样点在拟合得到的最小二乘平面上下均有分布。按照最小二乘评定法,选取与最小二乘平面平行的上下包容平面,计算得到平面度误差为:

σ=0.0540-(-0.0449)=0.0989mm

(14)

图4为平面度测量实验结果,展示了测头球心坐标拟合出的平面及侧视结果。以上实验结果表明本文的测量系统能够有效评定平面度的误差。

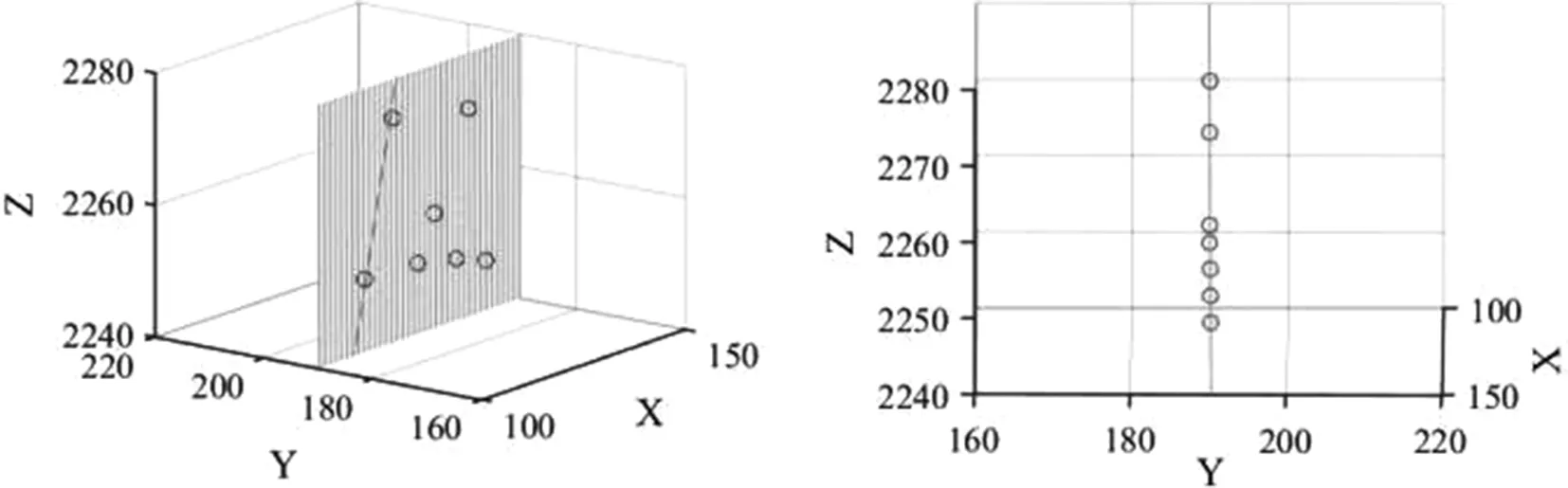
图4 平面度测量实验结果

4 总结

本文介绍了光学靶标式测量系统的系统组成、设计选型和基本解算实现;采用了一种回光编码标志点,能够实现准确的标志点中心提取和特征点匹配;设计了一种标志点和测头球形中心坐标的联合标定流程,以实现光学靶标的快速准确标定。最后,根据平面测量实验验证了系统的有效性。