基于可视图的职业教育网络关注度分析

周志辉

（湖南民族职业学院，湖南岳阳，414000）

引言

职业教育是我国教育体系的重要组成部分，是培养高素质人才的基础工程。2021 年和2022年，中共中央办公厅、国务院办公厅先后发布《关于推动现代职业教育高质量发展的意见》和《关于深化现代职业教育体系建设改革的意见》，明确了我国职业教育的改革蓝图，彰显出党和国家对职业教育的重视。与此同时，伴随着 “产教融合” “职普融通” “工匠精神” 等热词不断出现在网络媒体中，社会对职业教育给予了极大关注。作为衡量公众对某类事件的网络舆情关注程度的指标，网络关注度能够有效反映公众注意力资源在互联网中的分布情况。因此，观测以网民群体为代表的社会公众对职业教育的关注程度，可以折射出职业教育公众关注的状况。目前网络关注度研究侧重于旅游、健康、城市等方面[1~4]，对于职业教育的关注度分析则较少[5]，且通常使用莫兰指数、基尼系数等方法揭示关注度的时空特征，鲜有从复杂网络的角度分析职业教育关注度的网络特征、地区差异等。鉴于此，本文运用可视图方法[6，7]，将职业教育的百度指数时间序列转换为网络，进而探讨全国及各省级行政区的职业教育关注度的网络特征及地区差异。

1 数据和方法

1.1 数据来源

本文数据来源于百度指数。截至2022 年6月，中国网民规模达10.51 亿。百度搜索在网络搜索引擎用户中的渗透率达到90.9%，是国内最大的中文搜索引擎。百度指数是以百度海量网民行为数据为基础的数据分析平台，是当前互联网时代最重要的统计分析平台之一。百度指数的主要功能模块有趋势研究、需求图谱、人群画像。在趋势研究中，搜索指数是最主要的指标之一。搜索指数反映互联网用户对关键词搜索的关注程度及持续变化情况。它以网民在百度的搜索量为数据基础，以关键词为统计对象，科学分析并计算出各个关键词在百度网页搜索中搜索频次的权数。搜索指数数据来源包括PC 搜索和移动搜索。

本文采集全国（34 个省级行政区）2013 年1月1 日至2022 年12 月31 日关键词为 “职业教育” 的、以周为单位的PC 搜索和移动搜索的百度指数数据。由于青海、台湾、西藏、香港和澳门的数据缺项率达到20%以上，故最终采用全国（29个省级行政区）的数据进行分析。

1.2 研究方法

1.2.1 可视图

一个复杂网络可以表示为一个图模型。一个无向图G 是一个二元组(V,E)，其中V 称为节点集，E称为边集，E与V不相交。记N = |V|为节点数，M = |E|为边数。2008 年Lacasa 提出可视图构造方法，实现了从时间序列到复杂网络的转换。具体算法思想如下：

(1)给定时间序列Xn={ x1,x2,…,xn}，其中xi表示在i时刻时间序列采样点的值。

(2)在可视图中，Xn的每个时间序列采样点作为可视图的一个节点，即vi= xi。

(3)边由如下规则确定:

其中a < b < c。如果xa，xc满足上述关系，则va和vc之间存在边相连，即(va,vc) ∈E。

(4)按照上述方法遍历Xn所有序列点，即可完成可视图的构建。

1.2.2 主要网络参数

复杂网络的主要参数包括平均度、直径、平均路径长度、平均聚类系数等。

（1）平均度

节点vi的度ki表示该节点和其他节点之间的连接个数。平均度kˉ定义为所有节点的度的平均值，用于描述网络整体的连通程度，即

（2）直径和平均路径长度

节点vi和节点vj之间的距离dij定义为连接这两个节点的最短路径上的边数，这个参数可用来刻画节点间信息传递速度。网络中任意两个节点之间距离的最大值称为网络的直径D，即

网络的平均路径长度L 定义为任意两个节点之间的距离的平均值，即

（3）平均聚类系数

聚类系数用于描述网络中与同一节点相连的节点间也互为相邻节点的程度，反映网络节点的聚集性。用Ei表示节点vi的ki个相邻节点之间存在的边数，用Ci表示节点vi的ki个相邻节点之间可能存在的最大边数，则节点vi的聚类系数ci定义为Ei与Ci的比值，即

网络的平均聚类系数c 定义为所有节点聚类系数的平均值，即

1.2.3 度分布

度分布指网络中一个随机选择的节点的度为k 的概率。度分布可以刻画不同节点的重要性。度分布可用分布函数p(k)近似表示，p(k)为网络中度为k的节点数与总节点数的比例，即

其中Nk表示度为k 的节点数。如果一个网络表现出来的度分布特征为幂律分布p(k)~k-y，那么称这类网络为无标度网络。无标度网络同时具有鲁棒性和脆弱性。无标度网络对随机故障的容错能力强，但是若蓄意攻击枢纽节点，则网络结构很容易被破坏。

1.2.4 层次聚类

层次聚类是一种基于原型的聚类算法，试图在不同层次对数据集进行划分，从而形成树形的聚类结构。层次聚类方法的基本思想是:通过某种相似性测度计算节点之间的相似性，并按相似度由高到低排序，逐步重新连接各节点。该方法的优点是可随时停止划分。常用的相似性测度有欧氏距离、曼哈顿距离、马氏距离、相关系数、汉明距离等。本文采用欧氏距离进行聚类。对于两个n 维向量x =(x1, x2,…,xn)和y =(y1,y2,…,yn)，其欧氏距离为

2 网络关注度分析

2.1 可视图构建

数据采集时间为2013 年1 月1 日至2022 年12月31日，以周为单位，共有522个时间序列采样点。以全国数据为例，根据可视图构建方法，共产生522个节点和3115条边，得到如图1所示的可视图网络。利用同样的方法，可以构建29个省级行政区的可视图网络。

2.2 网络参数分析

根据可视图，计算出全国及29 个省级行政区可视图的主要网络参数值，见表1。

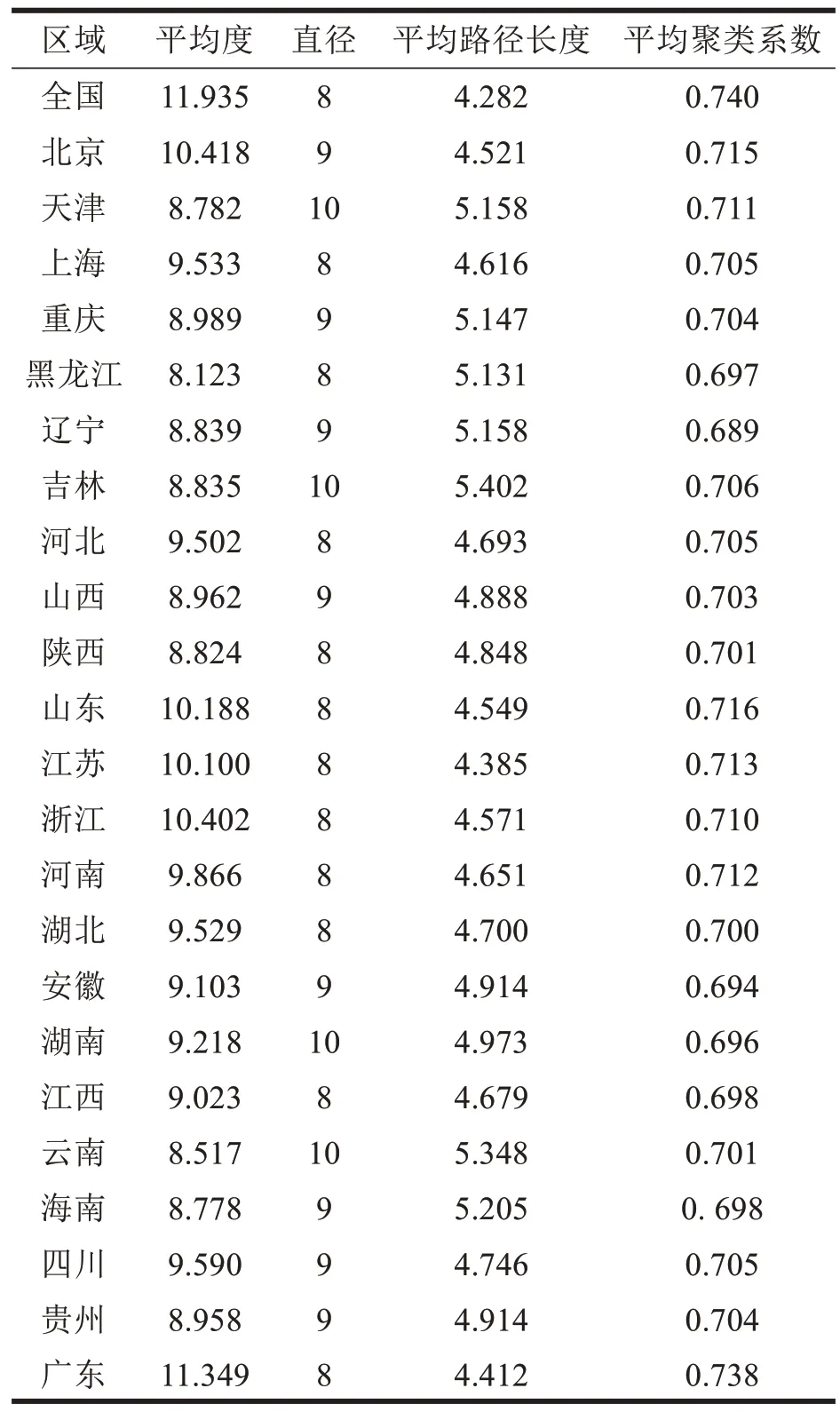
表1 全国及29 个省级行政区可视图的主要网络参数

从29个省级行政区的网络参数来看，广东、北京、浙江、山东、江苏的平均度较大、平均路径长度较小、平均聚类系数较大，说明这些省级行政区的网络整体连通性和聚集性更好、节点间信息传递速度更快;而新疆、内蒙古、甘肃、吉林、黑龙江等省级行政区的整体连通性和聚集性较弱。

2.3 无标度网络

根据式(6)，计算全国及29 个省级行政区的可视图网络度分布，结果见图2 和表2。从图2(a)可以看出，度值大的节点所占比例较小，大多数节点具有较小的度。在双对数坐标下，幂律分布表现为一条斜率为负数的直线，如图2(b)所示。这一线性关系是判断给定的实例中随机变量是否满足幂律的依据，因此全国的可视图网络是无标度网络。

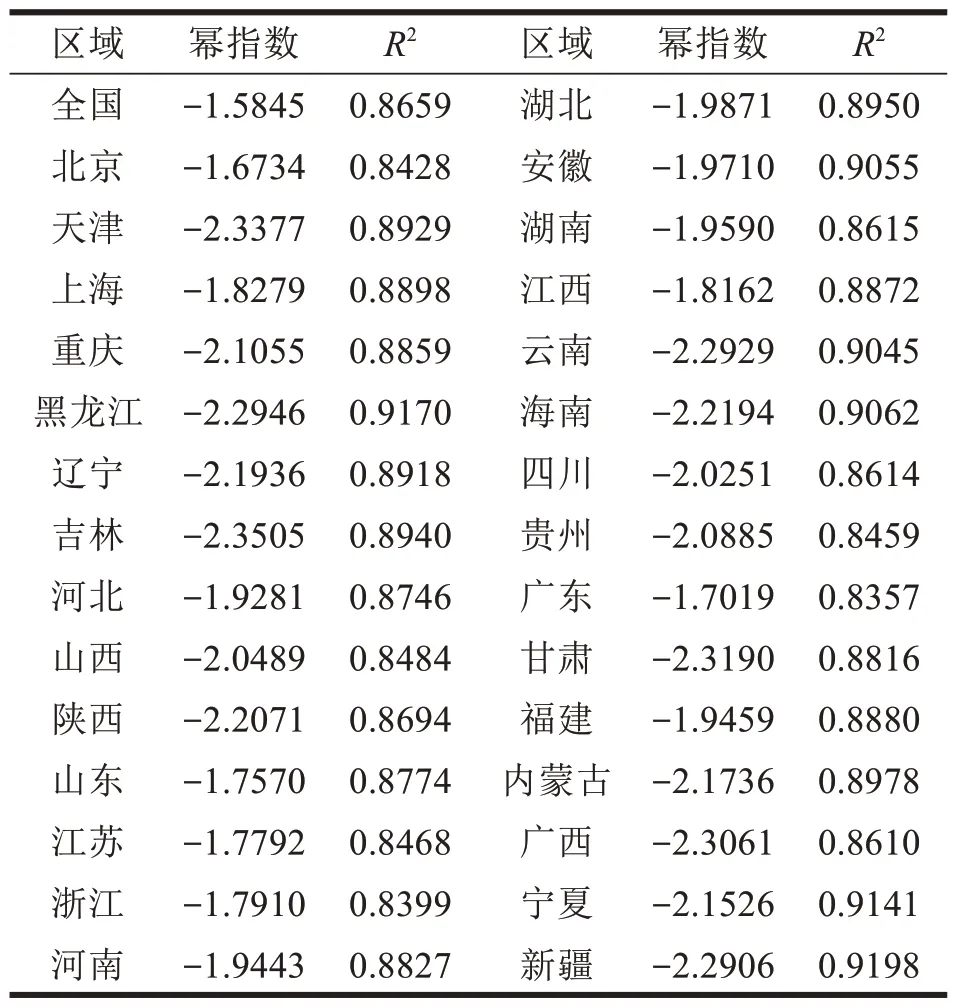
表2 全国及29 个省级行政区可视图的幂指数和R2

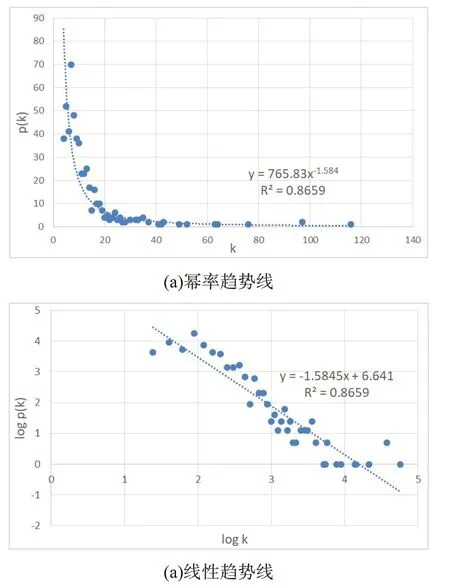
图2 可视图度分布(全国)

幂率分布的主要指数是幂指数。从表2可以看出，省级行政区的幂指数为-2.4 ~ -1.6，全国的幂指数最大，为-1.5845，这说明全国的原始时间序列数据波动性较小。R2可评估指标拟合优度，R2值越接近1，说明拟合质量越好。由表2 可知，全国及29 个省级行政区的R2均在0.8 以上，说明回归直线的拟合度很好。

2.4 聚类分析

采用层次聚类法对29个省级行政区的可视图网络进行聚类，结果如图3 所示。两个节点的纵轴高度值表示两个节点的聚类距离。可以看出，若将29 个省级行政区划分为两类，则广东、北京、山东、河南、江苏、浙江、河北、四川、上海、湖北、湖南是第一组，海南、宁夏、江西、重庆、辽宁、安徽、福建、山西、陕西、云南、广西、贵州、天津、新疆、内蒙古、甘肃、黑龙江、吉林是第二组。第一组的网络平均度较大、平均路径长度较小，表明节点之间关系较密切，这些省级行政区的职业教育关注度相对较高。第二组的网络平均度较小、平均路径长度较大，表明节点关系较弱，这些省级行政区的职业教育关注度相对较低。如果分为四类，可将广东和北京从第一组中划分出来，海南和宁夏从第二组中划分出来。

图3 29 个省级行政区的可视图网络聚类结果

3 结论

公众对职业教育的网络关注度是衡量职业教育受重视程度的重要参数。本文使用全国及29 个省级行政区2013 年1 月1 日至2022 年12月31 日 “职业教育” 百度指数数据，将原始时间序列数据转化为可视图网络，为从网络的视角分析职业教育的社会关注度提供了一种参考。

通过可视图分析发现，全国及29 个省级行政区的可视图网络是无标度网络。29 个省级行政区对职业教育的关注度存在较大差异，广东、北京、山东等省级行政区的职业教育关注度较高，海南、宁夏、新疆、内蒙古等省级行政区的职业教育关注度较低。