立体几何中轨迹问题的方程解法探究
2023-10-16湖北省武汉市马房山中学鲁前国湖北省武汉市武昌区教育局教研培训中心
⦿ 湖北省武汉市马房山中学 鲁前国 ⦿ 湖北省武汉市武昌区教育局教研培训中心 刘 欣
立体几何中的动点轨迹问题,在每年的高考复习备考中绝对是一个不会被遗忘的专题,在高考试题中也时有出现,多以选择、填空题的形式呈现,立足于知识的交汇点设计试题,题型新颖灵活,考查各部分知识间的纵向和横向联系,考查学生的创新意识和创新能力,渗透数学思想方法,体现新课程标准的要求,突显数学核心素养.由于这类问题往往具有较为复杂的空间几何体的结构特征,因此很多学生常常束手无策.下面以两道高考真题为例,探究两种不同模式的解题途径,通过对比体验方程解法的魅力!
1 解法探究

思路一:要求交线长,首先必须明确交线是何种几何图形.球面与平面相交时,交线一定是圆,在本题中,球面与侧面BCC1B1的交线就是圆在侧面BCC1B1上的一部分,因此解决问题的关键,就是找到圆心的具体位置,求出半径和圆弧所对圆心角的大小.
解法1:如图1,取B1C1的中点E,BB1的中点F,CC1的中点G.

图1

又因为四棱柱ABCD-A1B1C1D1为直四棱柱,所以BB1⊥平面A1B1C1D1,于是所以BB1⊥D1E.而BB1∩B1C1=B1,所以D1E⊥侧面B1C1CB.

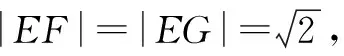



图2

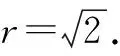
在坐标平面xBz内,令x=0,得F(0,1);令x=2,得G(2,1).

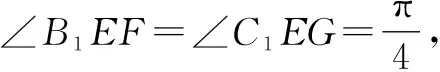

试题二(2006年北京卷)平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是( ).
A.一条直线 B.一个圆
C.一个椭圆 D.双曲线的一支
解法1:如图3,设l与l′是过定点A与AB垂直的任意两条直线,则这两条直线确定平面β,且斜线AB⊥平面β.过平面外一点有且只有一个平面与已知直线垂直,可知过定点A与AB垂直的所有直线都在平面β内,故动点C在平面β与平面α的交线上,问题转化为两平面的交线问题.

图3
故选择:A.
解法2:以B为原点,建立如图4所示的空间直角坐标系,其中x轴、y轴在平面α内,z轴垂直于平面α.

图4
设直线l上任意点P(x,y,z),A(a,b,c),则

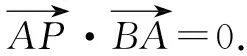
所以a(x-a)+b(y-b)+c(z-c)=0.
即ax+by+cz-(a2+b2+c2)=0.
令z=0,得坐标平面xBy即平面α内动点的轨迹方程为ax+by-(a2+b2+c2)=0,是一条直线.
故选:A.
解题思考:解法1中,动直线l形成过点A与AB垂直的平面β这一思维过程难度较大;解法2中用方程反映动直线上任意一点的空间变化规律,通过令z=0转化为平面内的变化规律,显得轻而易举!
2 解法应用
例题在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是边长为2的正方形,且PA=2.若点E,F分别为AB,AD的中点,则直线EF被四棱锥P-ABCD的外接球所截得的线段长为______.
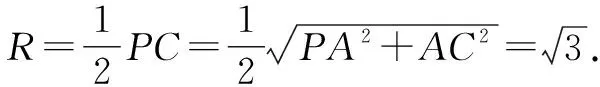
以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图5所示的空间直角坐标系,则E(1,0,0),F(0,1,0),O(1,1,1).

图5
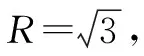
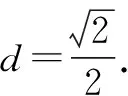
“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休”,这是华罗庚先生对数形结合思想的精辟描述.本文中笔者从方程的角度出发,将复杂的立体几何问题代数化,数形结合,相得益彰!
