基于因子分析和系统聚类的一次性纸杯XRF分析

陈壮，姜红

基于因子分析和系统聚类的一次性纸杯XRF分析

陈壮1，姜红2*

（1.甘肃政法大学 司法警察学院（公安分院），兰州 730070； 2.中国人民公安大学 侦查学院，北京 100038）

构建一次性纸杯物证分类新方法。利用X射线荧光光谱法（X-ray fluorescence spectrometry，XRF）对31个不同公司的一次性纸杯样品进行检验，并利用因子分析法确定光谱数据的2个主因子，2个主因子包含原始光谱数据79.209%的信息；利用2个主因子分别建立4个因子分析模型和因子得分函数，计算因子得分，用因子得分代替原始数据进行系统聚类；最后利用Fisher判别分析验证聚类结果的准确性和合理性，并利用定性半定量分析法进一步将一次性纸杯样品进行分类。将31个一次性纸杯样品分成3类时，同一公司的一次性纸杯样品聚为一类，样品的区分性较好，分类正确率为100%。利用X射线荧光光谱法、因子分析和系统聚类可实现一次性纸杯物证的无损、快速且有效的检验和分类。

X射线荧光光谱法；因子分析；系统聚类；判别分析；一次性纸杯

一次性纸杯是犯罪现场常见的物证，构建纸杯物证分类新方法将为基层公安工作带来新的思路。离子色谱法、X射线荧光光谱法（X-ray fluorescence spectrometry, XRF）、近红外光谱法等是检验纸张常用的方法[1-3]，部分方法存在有损、灵敏度低等不足。XRF是一种测定纸张所含元素种类及其含量的快速、无损且准确的检验方法。一次性纸杯的原材料为纸张，在再加工过程中会添加钛白粉（TiO2）、碳酸钙（CaCO3）等辅料，不同公司生产的一次性纸杯添加的辅料种类不同，使得一次性纸杯所含元素的种类及含量也不相同，这是检验并区分一次性纸杯的前提。

在法庭科学领域内对于XRF测定的光谱数据的分析处理，科研工作者通常直接对原始实验数据进行聚类、K均值、多元统计分析、主成分分析等处理[4-5]。基于多个化学指标变量的因子分析，采用聚类方法研究不同物证的分类尚未见报道。

这里采用X射线荧光光谱法对31个一次性纸杯样品进行检验，得到光谱数据，依据样品中元素的种类和含量的不同，利用因子分析法确定主因子，建立因子分析模型，计算因子得分，并进行系统聚类，最后验证一次性纸杯分类的准确性，利用定性半定量分析法进一步将一次性纸杯样品进行分类。文中构建了一种一次性纸杯物证分类新方法，拟为公安机关侦查破案提供新途径。

1 相关理论

1.1 因子分析

因子分析和主成分分析都是化学计量分析方法之一，二者有区别。主成分分析是将过多变量指标综合为少数几个概括性的新指标，以便对原始目标进行解释的一种降维方法。因子分析是主成分分析的延伸和推广，其基本思想是通过探究众多变量间协方差矩阵的内部疏密关系[6]，提取具有代表性且能综合所有变量信息的主因子，以便减少变量的数目，再现原始变量与因子之间的线性关系，并用主因子代替所有变量去分析整个问题[7]。

设若干样本、个变量指标为随机向量，=(1,2, …,X)T，主因子=(1,2, …,F)T，则因子分析模型[8]见式（1）—（3）。

……

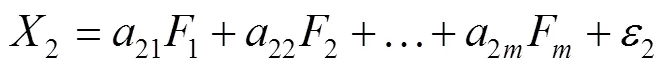
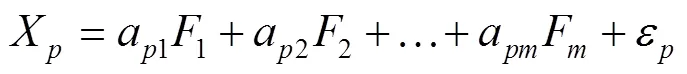
式中：a为因子载荷，矩阵=(a)，即因子载荷矩阵；为特殊因子。因子载荷反映变量X依赖主因子F的程度，即第变量X对于第主因子F的重要性，因子载荷通过方差最大正交旋转，得到新的因子载荷矩阵，使得因子分析模型更为合理[9]。

因子通常包括很多个子项，因子得分指这些子项按照一定的加权规则计算出来的数值，因子得分可以进一步对样本进行比较[10]。由因子分析模型导出因子得分函数，见式（4）。

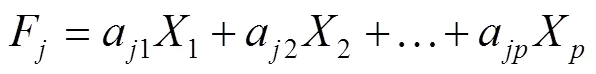
1.2 系统聚类

系统聚类是一门多元统计分类法。基本思想：将每个样品各看成一类，规定类与类之间的欧式距离，将最靠近的样品合并为新的一类，再将已聚合的新类和其他类按类间距离再合并，重复上述步骤，直至将所有的子类合为一类[12]。这里选择系统聚类中的最远邻元素法对因子得分进行聚类。

1.3 判别分析

判别分析是在聚类结果已明晰时，基于判别准则，建立判别函数，根据研究对象的特征值判别其归属于哪一组的统计判别和分组技术[13]。这里利用Fisher判别分析[14]验证基于因子得分的一次性纸杯样品系统聚类结果的准确性。

2 实验

2.1 样品收集

收集“味多美”“McDonald's”“西贝筱面村”等不同公司的一次性纸杯样品共31个，将其清洁干净后分别编号。其中，3#、4#样品来自同一公司（McDonald's），20#、21#、22#样品来自同一公司（妙洁），24#、31#样品来自同一公司。

2.2 仪器及条件

主要仪器：X-MET8000能量色散型XRF光谱仪，牛津仪器。实验条件：电压为40 kV，电流为50 μA，采样时间为110 s[15]。

2.3 方法

首先，利用实验仪器对31个一次性纸杯样品进行XRF检验，每个样品的测定时间为110 s，分别测定3次，取平均值，将平均值作为样品XRF光谱数据的最终测定结果。其次，利用SPSS Statistics 23.0软件将31个样品的XRF光谱数据分别进行标准化分析、因子分析，再确定主因子，建立因子分析模型，计算因子得分，并依据因子得分进行系统聚类。最后，对聚类结果进行判别检验。

3 结果与分析

3.1 一次性纸杯样品的XRF检验

检验结果表明，31个一次性纸杯样品所含的主要元素为Cl、Ca、Ti、Fe，且不同样品所含元素的种类和含量各不相同，在光谱曲线图中也有所差异，如图1所示。20#、21#、22#样品来自同一家公司（妙洁），其光谱曲线却明显不同。

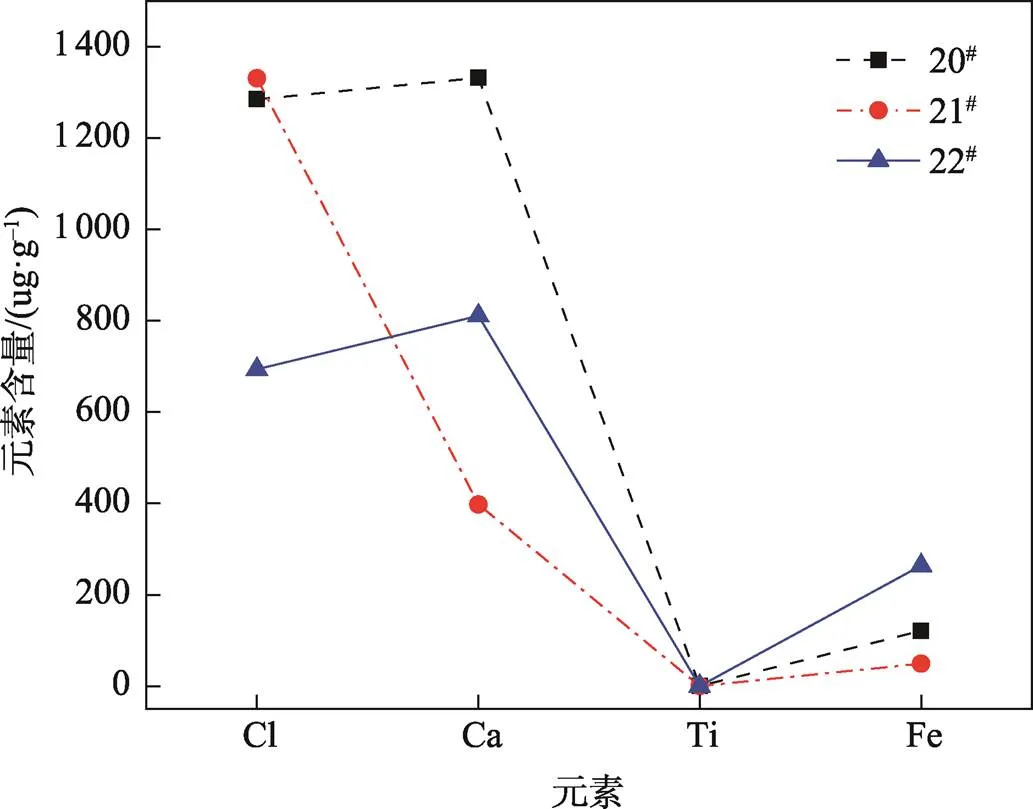
图1 20#、21#和22#的光谱曲线

3.2 数据标准化处理及因子分析的适用性检验

利用SPSS Statistics 23.0软件对光谱数据进行标准化处理，利用KMO检验和Bartlett球状检验对标准化处理后的光谱数据进行因子分析的适用性检验[16]。结果表明，KMO检验值为0.666，Bartlett球状检验sig值为0.05。上述2项检验结果表明，各元素变量之间具有相关性，因子分析有效，且适用性较好，可以得出较满意的因子分析模型。

3.3 一次性纸杯样品的XRF光谱数据因子分析

3.3.1 基于因子分析法确定主因子

对31个一次性纸杯样品光谱数据中的元素变量进行因子分析。利用因子分析法，将标准化后的实验数据中的Cl、Ca等4种元素变量降维，并进行线性组合，得到4个因子。4个因子解释了Cl、Ca、Ti、Fe等4种元素变量的全部信息，各因子的特征值和贡献率如表1所示。在实际应用中，往往取特征值大于1的因子为主因子。由表1可知，前2个因子的特征值大于1，包含了一次性纸杯中测定的Cl、Ca等4种元素变量79.209%的信息，具有一定的代表性，可以作为新的具有实际意义的一次性纸杯分类综合指标。

表1 各因子的特征值和贡献率

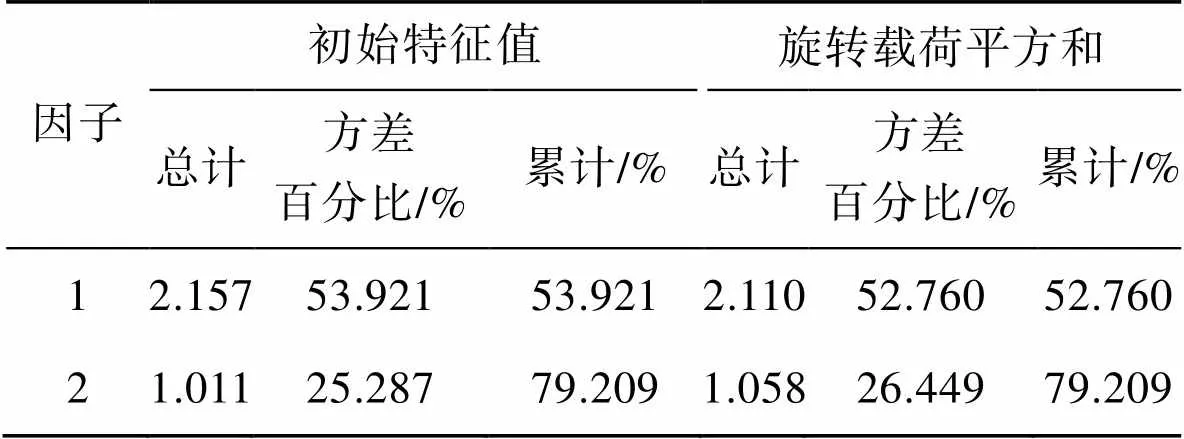
Tab.1 Eigenvalue and contribution rate of each factor

3.3.2 建立因子分析模型及计算因子得分

经标准化处理后，将光谱数据中Cl、Ca、Ti、Fe等4种元素的指标分别设定为1、2、3、4，2个主因子分别设定为1和2。对初始因子载荷矩阵进行最大方差旋转，并建立一次性纸杯分类指标的因子分析模型，见式（5）—（8）。

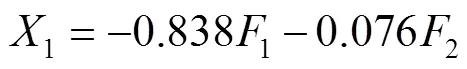
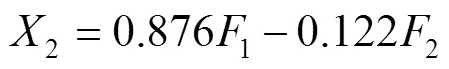
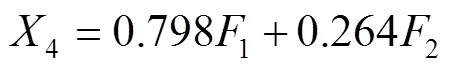
由因子分析模型可知，第1个主因子1主要由Cl、Ca、Fe 3项指标决定，这3项指标除了4在主因子1上的载荷为79%以上，其余2项指标在主因子1上的载荷均超过83%。第2个主因子2由Ti元素的变量指标决定，且此项指标在主因子2上的载荷超过98%。利用回归方法求得因子得分系数矩阵[17]，结果见表2。

表2 因子得分系数矩阵

Tab.2 Factor score coefficient matrix

根据表2，建立了因子得分函数，见式（9）—（10）。

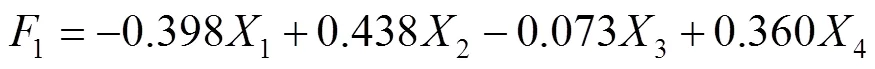
根据式（9）—（10）计算因子得分，结果见表3。

表3 因子得分汇总

Tab.3 Summary of factor scores

3.4 基于因子得分的一次性纸杯样品系统聚类分析

利用SPSS Statistics 23.0软件，用2个主因子得分代替原始光谱数据作为新的变量进行系统聚类，聚类结果如图2所示。

图2 31个一次性纸杯样品的聚类分析结果

如果类间距离不同，则聚类结果不同。选择合适的类间距离可将同一公司的一次性纸杯样品聚为同一类。由图2可知，当类间距离为5时，可将31个一次性纸杯样品聚为3类，聚类结果见表4。

表4 在类间距离为5时一次性纸杯样品的聚类结果

Tab.4 Clustering results of disposable paper cup samples when inter-class distance is 5

一次性纸杯作为一种纸容器，由化学木浆经过机械加工、胶黏等一系列工艺制成。由于不同生产厂家的制造工艺不同，因此纸杯所含的元素和含量也不同。利用因子分析和系统聚类分析可以客观地分析一次性纸杯的X射线荧光光谱数据，将来自同一厂家的一次性纸杯样品聚成一类。由表4可知，当类间距离为5时，来自“McDonald's”公司的一次性纸杯样品（3#和4#样品）被分在同一类别，来自“妙洁”公司的一次性纸杯样品（20#、21#、22#样品）被分在同一类别。由此可知，将31个一次性纸杯样品聚为3类时，部分公司所生产的一次性纸杯样品的聚合性较好。

3.5 聚类结果的判别分析

利用Fisher判别分析验证上述聚类结果的准确性。当类间距离为5时，利用因子分析和系统聚类将31个一次性纸杯样品分为3类。根据聚类结果，建立了2个判别函数，判别函数的具体信息见表5。由表5可知，判别函数1和判别函数2的特征值的方差贡献率分别为87.400%和12.600%，并且典型相关性分别为0.968、0.824，说明可以将2个判别函数作为判别一次性纸杯样品系统聚类结果准确性的依据。

表5 判别函数的具体信息

Tab.5 Discriminant function details

从一次性纸杯样品的聚类结果可知，如果类间距离不同，则聚类数不同，进而各类别样品的组质心在Fisher判别函数图的分布情况也不相同。当类间距离为5时，一次性纸杯样品被分成3类，各组质心在Fisher判别函数的分布情况如图3所示。由图3可知，当类间距离为5时，各组质心分散均匀，不同组间的样品具有较强的区分性。

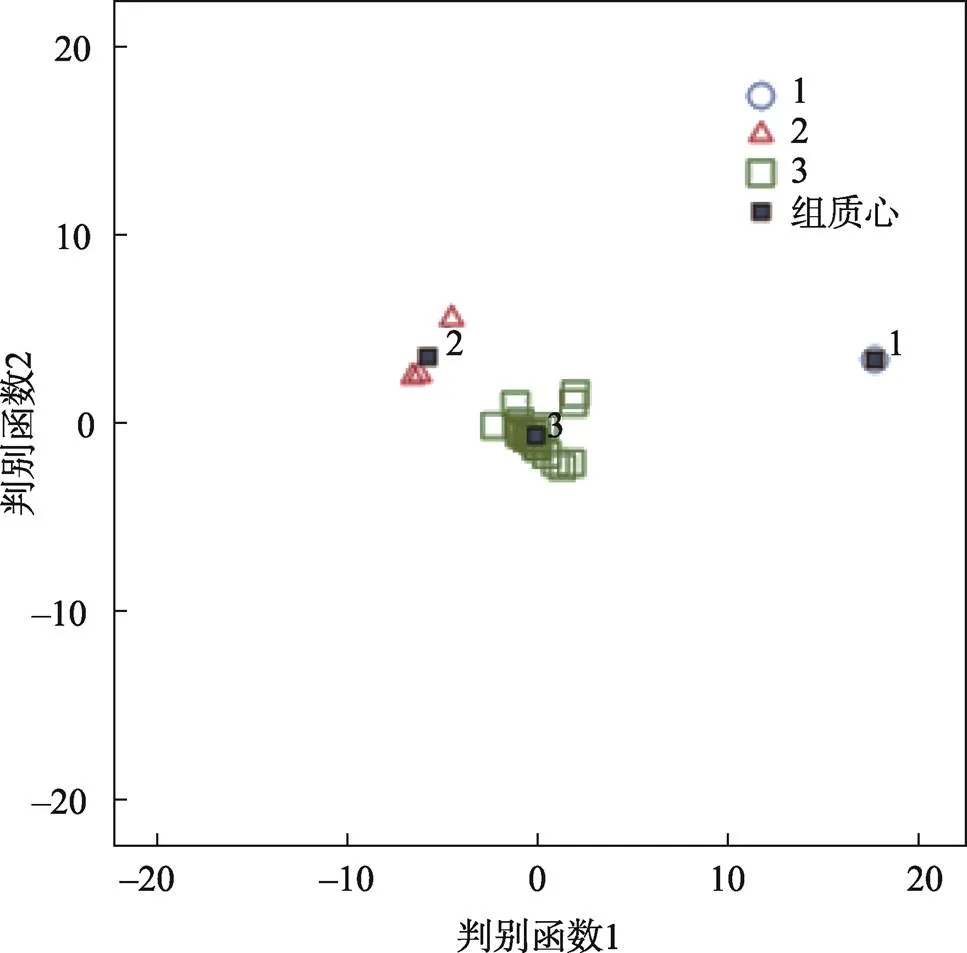
图3 判别函数分布

利用Fisher判别函数模型对31个一次性纸杯样品进行原始分类验证和交叉分类验证。结果表明，当31个一次性纸杯样品被分为3类时，原始分类的正确率为100%，交叉验证的正确率为96.8%，表明基于因子分析的聚类分析能正确地识别一次性纸杯样品分类。

为了满足公安机关获取更多侦查信息的破案需求，可以利用定性半定量分析法对同类一次性纸杯样品进行区分。以类别3为例，依据是否含有Ti元素，将一次性纸杯样品分成2类，进一步分类结果如图4所示。

图4 类别3一次性纸杯样品进一步分类结果

4 结论

利用X射线荧光光谱法对一次性纸杯中所含的元素及其含量进行了检验，基于因子分析和系统聚类挖掘了各变量指标之间的内在关系，实现了一次性纸杯的光谱分析，构建了一次性纸杯分类的新方法。同时建立了因子分析模型和因子得分函数，分析了主因子与原始变量指标间的线性关系，并且利用Fisher判别分析建立了判别函数，验证了分类结果准确性。结合公安机关侦查破案的实际需求，利用定性半定量法进一步对一次性纸杯样品进行了分类。

今后应着重研究一次性纸杯样品量的扩充、多种检验方法的比较、数据处理方法的优化、在公安机关的实际运用等方面，进一步推进法庭科学领域内纸张检验鉴定的发展。

[1] 刘彤彤. 离子色谱法在纸张鉴别中的应用[J]. 中国刑警学院学报, 2021(4): 118-123.

LIU Tong-tong. Application of Ion Chromatography in Paper Identification[J]. Journal of Criminal Investigation Police University of China, 2021(4): 118-123.

[2] 李春宇, 刘金坤, 姜红, 等. 基于支持向量机算法的X射线荧光光谱纸张灰烬识别研究[J]. 激光与光电子学进展, 2021, 58(3): 358-364.

LI Chun-yu, LIU Jin-kun, JIANG Hong, et al. Identification of X-Ray Fluorescent Spectral Paper Ashes Based on Support Vector Machine Algorithm[J]. Laser & Optoelectronics Progress, 2021, 58(3): 358-364.

[3] 夏静静, 杜夏瑜, 闫红, 等. 基于卷积神经网络的纸张年代红外光谱分类建模方法研究[J]. 光谱学与光谱分析, 2020, 40(S1): 61-62.

XIA Jing-jing, DU Xia-yu, YAN Hong, et al. Research on Paper Age Classification Model Based on Convolutional Neural Network[J]. Spectroscopy and Spectral Analysis, 2020, 40(S1): 61-62.

[4] 姜红, 鞠晨阳, 务瑞杰, 等. 聚类分析法的塑料饮料瓶光谱分析[J]. 红外与激光工程, 2018, 47(8): 358-363.

JIANG Hong, JU Chen-yang, WU Rui-jie, et al. Spectral Analysis of Plastic Beverage Bottles Based on Cluster Analysis[J]. Infrared and Laser Engineering, 2018, 47(8): 358-363.

[5] 陈壮, 姜红, 郝丁成, 等. 基于K-means和簇内误差平方和的塑料快递包装袋X射线荧光光谱检验[J]. 激光与光电子学进展, 2022, 59(11): 489-495.

CHEN Zhuang, JIANG Hong, HAO Ding-cheng, et al. X-Ray Fluorescence Spectral Inspection of Plastic Express Packaging Bags Based on K-Means and Within-Cluster Sum of Squared Errors[J]. Laser & Optoelectronics Progress, 2022, 59(11): 489-495.

[6] 孙德山. 主成分分析与因子分析关系探讨及软件实现[J]. 统计与决策, 2008(13): 153-155.

SUN De-shan. Discussion on the Relationship between Principal Component Analysis and Factor Analysis and Its Software Implementation[J]. Statistics & Decision, 2008(13): 153-155.

[7] 林海明, 张文霖. 主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J]. 统计研究, 2005, 22(3): 65-69.

LIN Hai-ming, ZHANG Wen-lin. The Relationship between Principal Component Analysis and Factor Analysis and SPSS Software—To Discuss with Comrade Liu Yumei, Lu Wendai Etc[J]. Statistical Research, 2005, 22(3): 65-69.

[8] 林海明, 刘照德, 詹秋泉. 因子分析综合评价应该注意的问题[J]. 数理统计与管理, 2019, 38(6): 1037-1047.

LIN Hai-ming, LIU Zhao-de, ZHAN Qiu-quan. Issues that should be Noted on Factor Analysis for Comprehensive Evaluation[J]. Journal of Applied Statistics and Management, 2019, 38(6): 1037-1047.

[9] TSOULFIDIS L, ATHANASIADIS I. A New Method of Identifying Key Industries: A Principal Component Analysis[J]. Journal of Economic Structures, 2022, 11(1): 1-23.

[10] 赵慧琴, 石立, 刘金山, 等. SPSS软件计算主成分分析的缺陷与纠正[J]. 统计与决策, 2020, 36(15): 56-59.

ZHAO Hui-qin, SHI Li, LIU Jin-shan, et al. Defects and Correction of Principal Component Analysis in SPSS Software Calculation[J]. Statistics & Decision, 2020, 36(15): 56-59.

[11] TEKLER D Z, LOW R, CHUNG Y S, et al. A Waste Management Behavioural Framework of Singapore's Food Manufacturing Industry Using Factor Analysis[J]. Procedia CIRP, 2019, 80: 578-583.

[12] 田兵. 系统聚类法及其应用研究[J]. 阴山学刊(自然科学版), 2014, 28(2): 11-16.

TIAN Bing. Hierarchical Clustering Method and Its Research about Application[J]. Yinshan Academic Journal (Natural Science Edition), 2014, 28(2): 11-16.

[13] 刘曙, 张博, 闵红, 等. X射线荧光光谱结合判别分析识别铁矿石产地及品牌: 应用拓展[J]. 光谱学与光谱分析, 2021, 41(1): 285-291.

LIU Shu, ZHANG Bo, MIN Hong, et al. X-Ray Fluorescence Spectroscopy Combined with Discriminant Analysis to Identify Imported Iron Ore Origin and Brand: Application Development[J]. Spectroscopy and Spectral Analysis, 2021, 41(1): 285-291.

[14] 朱晓晗, 姜红, 崔傲松, 等. 基于Fisher判别分析的一次性塑料手套光谱鉴别[J]. 塑料工业, 2020, 48(7): 108-112.

ZHU Xiao-han, JIANG Hong, CUI Ao-song, et al. Spectrum Identification of Disposable Plastic Gloves Based on Fisher Discriminant Analysis[J]. China Plastics Industry, 2020, 48(7): 108-112.

[15] 陈壮, 姜红, 李春宇, 等. X射线荧光光谱法检验一次性纸杯的研究[J]. 中华纸业, 2018, 39(22): 32-36.

CHEN Zhuang, JIANG Hong, LI Chun-yu, et al. A Study on Disposable Paper Cups Tested by X-Ray Fluorescence Spectroscopy[J]. China Pulp & Paper Industry, 2018, 39(22): 32-36.

[16] 解坤, 张俊芳. 基于KMO-Bartlett典型风速选取的PCA-WNN短期风速预测[J]. 发电设备, 2017, 31(2): 86-91.

XIE Kun, ZHANG Jun-fang. Short-Term Wind Speed Forecasting Using PCA-WNN Based on KMO-Bartlett Typical Wind Speed Selection[J]. Power Equipment, 2017, 31(2): 86-91.

[17] BAUNACK S, OSWALD S. Application of Factor Analysis in Electron Spectrometry (AES, XPS) for Materials Science[J]. International Journal of Materials Research, 2022, 96(9): 972-982.

X-ray Fluorescence Spectrum Analysis of Disposable Paper Cups Based on Factor Analysis and Systematic Clustering

CHEN Zhuang1, JIANG Hong2*

(1. Judicial Police Academy (Public Security Branch),Gansu University of Political Science and Law, Lanzhou 730070, China; 2. School of Criminal Investigation, People's Public Security University of China, Beijing 100038, China)

The work aims to develop a new method for classifying paper cup evidences. Thirty-one disposable paper cups from different manufacturers were tested through X-ray fluorescence spectrometry. Meanwhile, for spectral data, two main factors containing 79.209% of the information of the original spectral data were determined by factor analysis. Four factor analysis models and factor score functions were established with the two main factors so as to calculate the factor score, and then the original data were replaced by factor scores for systematic clustering. Finally, Fisher's discriminant analysis was performed to verify the accuracy and reasonableness of the clustering results. When 31 disposable paper cup samples were divided into three categories, the disposable paper cup samples of the same company were grouped into one category. The samples had good discrimination, and the classification accuracy was 100%. By means of X-ray fluorescence spectrometry, factor analysis and systematic clustering, the nondestructive, rapid and effective inspections as well as classification of different paper cups can be achieved with accurate and reliable results.

X-ray fluorescence spectrometry; factor analysis; systematic clustering;discriminant analysis; disposable paper cup

TS7；TB99

A

1001-3563(2023)19-0217-06

10.19554/j.cnki.1001-3563.2023.19.028

2022-05-13

甘肃政法大学“引才专项项目”（gszf2020xyc004）

责任编辑：彭颋