基于3-(RRR)E(RR)S并联机构的多运动模式分析

申博，郭文孝，李瑞琴*

基于3-(RRR)E(RR)S并联机构的多运动模式分析

申博1，郭文孝2,3，李瑞琴3*

（1.山西水利职业技术学院 机电工程系，太原 030032；2.中国煤炭科工集团太原研究院有限公司，太原 030006；3.中北大学 机械工程学院，太原 030051）

多模式机器人具有智能型可重构和变结构特性的能力，能够主动或被动适应多变的环境，设计一种能够在包装工程领域应用的多运动模式并联机构。从螺旋理论出发，通过研究线矢量与偶量在不同几何空间中的相关性，得出在一定条件下约束力可以转化为法向约束力偶，为并联机构实现多模式运动提供了理论支撑。通过3-(RRR)E(RR)S并联机构变形，得出该机构的具有3R、2T1R和2R1T等3种运动模式，在各种运动模式下的自由度均为3，具有全周性。基于3-(RRR)E(RR)S并联机构，通过变化支链约束力线矢空间位置关系来改变机构的约束条件，使该并联机构能够实现3R、2T1R和2R1T多模式运动，满足物流分拣、抓放定位、产品空间姿态调整等需求。

多运动模式；并联机构；螺旋理论；自由度

随着智能制造和机器人技术的快速发展，要求机器人能够主动或被动地适应不同工况、任务和多变的环境，具有智能型可重构和变结构特性的能力[1]。目前，多运动模式的并联机构在航天领域[2-4]、先进制造业[5-7]、医疗康复[8-10]等领域有着迫切的需求。在包装生产线，一般由搬运、包装、打码、装箱或堆垛等多个任务和多个工作环节组成，每个环节采用单一运动模式工业机器人。多运动模式机器人的不同运动模式可对应不同的工作任务或工作状态，可实现一机多用。Ferdinando等[11]首次提出变胞机构，并将其应用于纸盒折叠。陈辉庆[12]研究了面向制糖业中的码垛任务的可控变胞机构的动态可靠性。多运动模式机器人可满足多任务、多工作环节场合的需求，因此在包装生产线中具有广泛的前景[13-14]，但是相关研究比较少，因此该类型机构进入国内外研究者的视线，并引起了广泛关注。

多运动模式机构主要指可以有多种运动形式的机构[15]，与运动分岔机构[16]、变胞机构[17-19]等均属于可重构机构。Kong等[20]提出了一种具有多种工作模式的并联机构型综合的通用方法，并构型综合出同时具有球面和平移模式的3-DOF并联机构。Fan等[21]基于构型演化与李群理论的结合，提出了一种多运动模式的并联机构构型综合方法，综合了两平移两转动（2T2R）自由度、一平移两转动（1T2R）自由度和两转动（2R）自由度并联机构。Li等[22]利用位移群理论，主要研究一类特殊动平台可以经历Schoenflies运动的分岔的并联机构。叶伟等[23]将一种具备2种运动模式的机构引入并联机构支链，提出了一种具有运动分岔特性的并联机构。石志新等[24]利用方位特征集方法，提出了多模式并联机构的结构类型综合方法以及操作模式分析方法。张春燕等[25]针对移动机构多运动模式的功能需求，提出基于单环运动链的设计方案。虽然有不少学者开展了多模式运动机构的研究，但其发展还是处于初级阶段，还难以满足工程应用领域的需求，还有诸多问题亟须研究解决[26]。

在分拣、抓放、装箱等包装工程领域，不仅需要2T1R机构进行流水线抓放定位、2R1T机构进行分拣，还需要3R机构调整产品空间姿态。针对这一问题，将应用螺旋理论和Grassman线几何，通过研究线矢量与偶量的相关性，分析多运动模式转化的条件。在此基础上，提出一种3-(RRR)E(RR)S新型的多运动模式并联机构，分析其运动模式。

1 多运动模式并联机构的分析

1.1 螺旋理论

根据螺旋理论[27]可知，空间直线和螺旋之间存在一一对应关系，其中螺旋的表达式见式（1）。

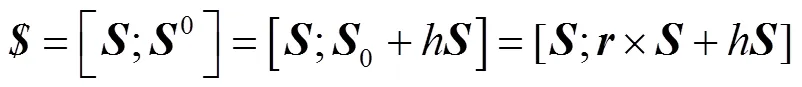
式中：为螺旋的主部，也是螺旋方向矢量；0为螺旋的对偶部；0为螺旋的线距；为从坐标原点到螺旋轴线上任意一点的矢径；为螺旋的节距。

在式（1）中，当•0≠0时，为一般意义的螺旋，此时≠0；当≠0、0≠0、•0=0时，退化为线矢量，线矢的节距=0；当=0、0≠0，退化为偶量；当=0、0=0，该螺旋为零，节距为不定值。

螺旋通常也用Plücker坐标表示，其中含有6个标量，形式见式（2）。

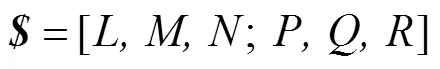
式中：(，，）为螺旋的底部；(，，）为螺旋的对偶部。

当式（2）的螺旋表示运动时，前3个螺旋可以表示转动运动，后3个螺旋表示移动运动；当其表示力螺旋时，前3个螺旋表示力，后3个则是力偶；当表示约束时，前3个螺旋表示约束力，后3个表示约束力偶；在表示自由度时，前3个表示转动自由度，后3个表示移动自由度。本文将上述螺旋理论对多运动模式并联机构进行分析研究，文中将采用如表1所示的箭头来代表运动螺旋、约束、自由度。

表1 采用箭头的类型和所代表的意义

Tab.1 Types and meanings of arrows adopted

1.2 多运动模式转化的条件

众所周知，空间不受任何约束物体的自由度是6，即沿、、轴的3个移动和绕、、轴的3个转动，如图1所示。当物体受到约束力或者约束力偶的作用，相应方向的移动或者转动被约束。并联机构多运动模式转换，就是通过改变机构的约束条件，即作用到动平台上的约束力和约束力偶之间的转化，可以实现运动模式的变化。

图1 空间物体的运动

并联机构动平台的约束螺旋系为各支链运动螺旋系的反螺旋集合，假设其运动模式发生转化，则支链对动平台的结构约束发生了变化。在机构自由度不变且具有多运动模式时，就需要研究线矢量与偶量的相关性。

线矢量与偶量的相关性，可分为3类情况。

1）两平行线矢和一法向偶量。如果空间有3个螺旋，1、2和3。前2个是线矢量且空间平行，第3个是偶量，且与前2个线矢量组成的平面垂直，如图2所示。在图2中，1、2和3的表达式见式（3）。

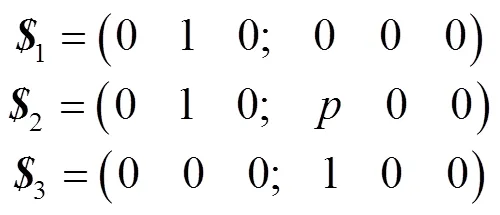
求得式（3）的基础螺旋系见式（4）。

由式（4）可知，1，2和3螺旋系的秩为2，其基础螺旋为一线矢和一法向偶量。由此可知当两线矢平行时，可以等效为一线矢和一法向偶量，即两平行线矢中的一个转化为法向偶量。

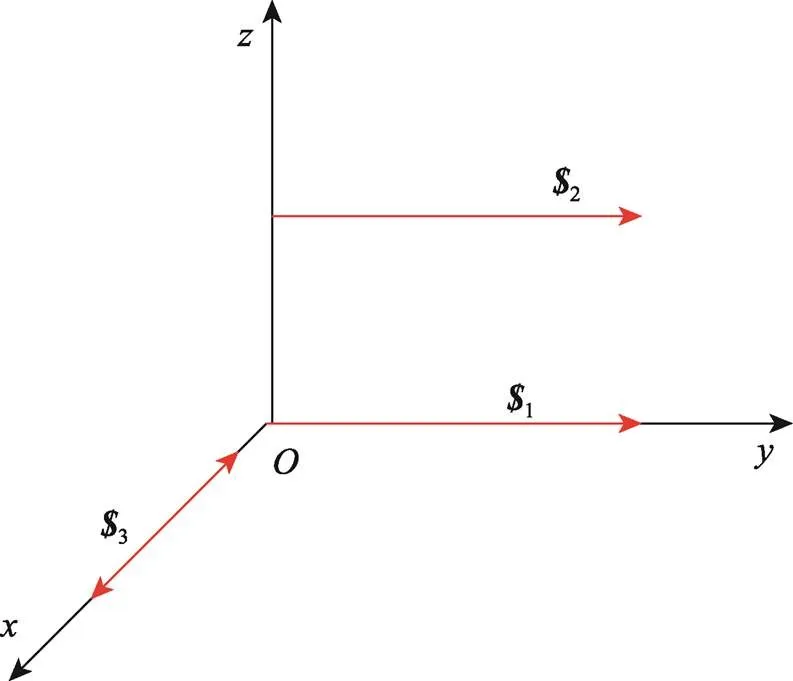
图2 两平行线矢和一法向偶量

2）平面三线矢和一法向偶量。如果空间有4个螺旋，1、2、3和4。前3个是线矢量且共面，第4个是偶量，且与前3个线矢量组成的平面垂直，如图3所示。在图3中，1、2、3和4的表达式见式（5）。

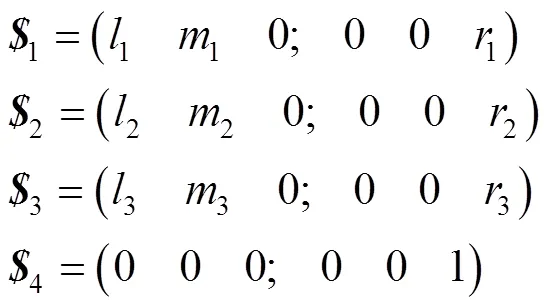
求得式（5）的基础螺旋系见式（6）。

对式（4）进行分析，1、2、3和4螺旋系的秩为3，由此可知当三线矢共面时，可以等效为平面两线矢和一法向偶量，即共面三线矢中的一个转化为法向偶量。

3）空间平行三线矢和一个相垂直向偶量。如果空间有4个螺旋，1、2、3和4。前3个是线矢量且空间平行，第4个是偶量，且与前3个线矢量相垂直，如图4所示。在图3中，1、2、3和4的表达式见式（7）。

求得式（7）的基础螺旋系见式（8）。

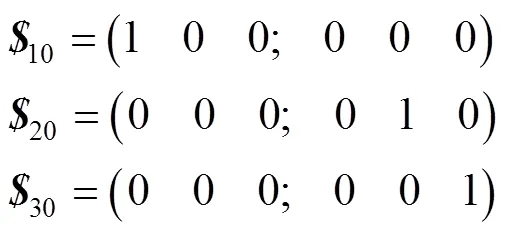
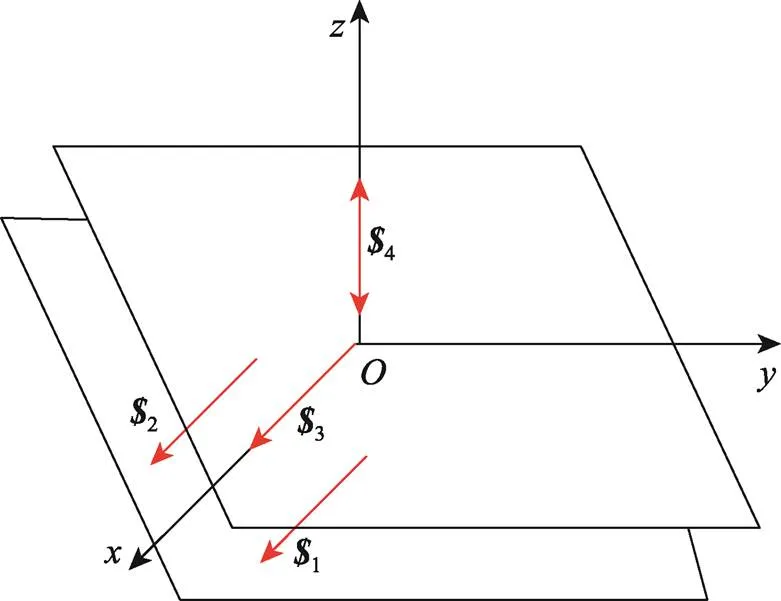
图4 空间平行三线矢和一个相垂直向偶量

由式（8）可知，空间平行三线矢等效为一线矢和两法向偶量，即空间平行三线矢中两线矢转化为两法向偶量。

综合分析线矢和偶量的相关性可知，当线矢和偶量存在线性相关时，其中部分线矢量可等效为法向偶量。由此可知，运动支链对动平台的约束力线矢平行或三力线矢共面时，机构的运动模式就发生了改变。

2 机构描述及各运动模式分析

3-(RRR)E(RR)S并联机构，每条运动支链都由5个转动副组成，前2个转动副轴线相交，而最后3个转动副轴线平行，其中第1个转动副S与静平台相连，最后1个转动副RE与动平台相连，如图5所示。选取其中一条支链，在转动副轴线相交点建立坐标系原点，轴与平行转动副轴线平行，如图6所示。以此坐标系可以建立该支链的5个运动螺旋的表达式如下：

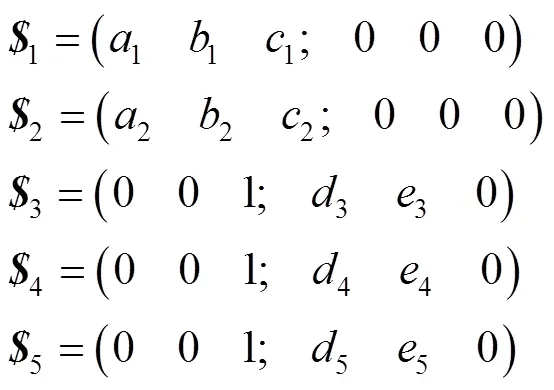
式（9）的反螺旋为：

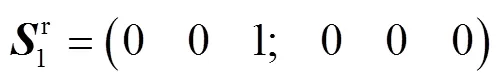
由式（10）可知，该支链的反螺旋为过转动副轴线RS并相交的点，方向平行于转动副RE轴线的力线矢。

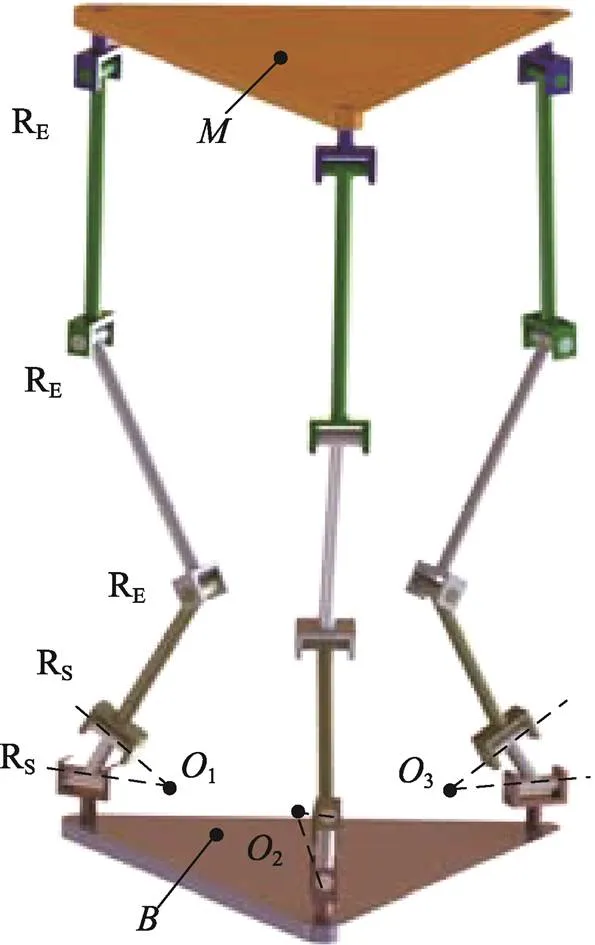
图5 3-(RRR)E(RR)S并联机构

2.1 2R1T运动模式分析

在装配时，转动副RE的轴线平行于动平台，与动平台连接的3个转动副RE的轴线满足共面不汇交。考虑到机构的3条支链均为(RRR)E(RR)S，每条支链有一个约束力线矢，3条支链共作用3个约束力线矢于动平台。此时，动平台的3个约束力线矢平行于动平台，满足共面相交但不汇交。在静平台上建立如图7所示坐标系，可以写出约束力分别为：

图6 (RRR)E(RR)S运动支链

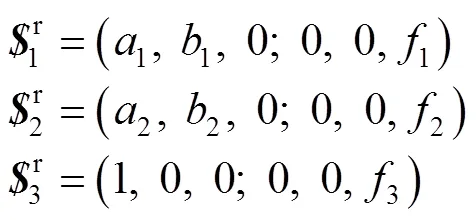
式中：(a1, b1, 0)和(a2, b2, 0)为约束力线矢的方向；f1、f2和f3分别为约束力线矢线距的z向分量。

由式（11）可知，约束螺旋系的秩为3，没有公共约束，按照修正的G-K公式计算：

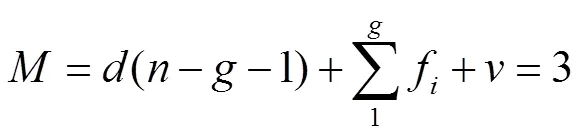
由此可知，此时3-(RRR)E(RR)S并联机构的自由度是3。为研究这3个自由度的性质，对式（11）进行反螺旋变化，可得基础运动螺旋系为：

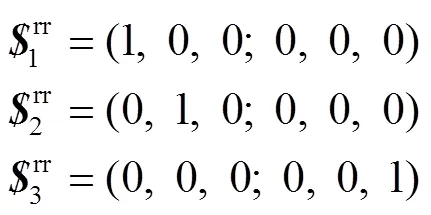
由式（13）可知，动平台的自由度性质为、方向的转动和方向的移动，即为2R1T。

由线矢量与偶量的相关性可知：动平台受到共面三约束力线矢时，可以等效为平面两约束力线矢和一法向约束力偶。约束力线矢限制了平面的两移动，约束力偶限制了平面法向的转动。由此可知，3条支链的转动副RE的轴线共面不汇交时，3-(RRR)E(RR)S并联机构的运动模式为2R1T。

当动平台沿轴的移动，动平台的约束螺旋不改变，机构的运动模式依然为2R1T；当动平台绕、轴的转动，约束力线矢依然过转动副RS轴线的交点，且方向平行于对应支链转动副RE副的轴线，即约束力线矢位置关系没有改变，动平台的约束螺旋不改变，则运动性质不发生改变。由此可知，在RE副轴线共面相交但不汇交的布置情况下，3-(RRR)E(RR)S并联机构的运动模式为2R1T，且具有全周性。物流分拣货物中，动平台需要绕轴、轴转动和沿轴移动。在2R1T运动模式下，动平台可实现绕、轴转动和沿轴移动，满足物流分拣需求。

2.2 2T1R运动模式分析

在装配时，转动副RE的轴线平行于动平台，与动平台连接的3个转动副RE的轴线空间平行。此时，动平台的3个约束力线矢平行于动平台，满足空间平行。在静平台上建立如图8所示坐标系，可以写出约束力见式（14）。

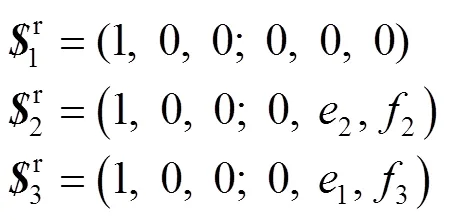
式中：(0，e2，f2)和(0，e3，f3)为约束力的线距。

由于3个约束力线性无关，则没有公共约束，应用修正的G-K公式可得此时机构自由度见式（15）。

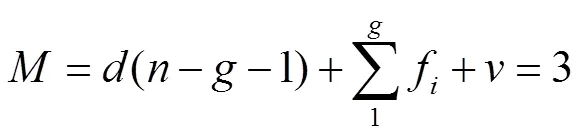
由此看到，此时3-(RRR)E(RR)S并联机构的自由度为3。为研究这3个自由度的性质，对式（14）进行反螺旋变化，可得基础运动螺旋系见式（16）。

由式（13）可知，动平台的自由度性质为、方向的移动和方向的转动，即为2T1R。

由线矢量与偶量的相关性可知，动平台受到空间平行三约束力线矢时，可以等效为一约束力线矢和两法向约束力偶。约束力线矢限制了该方向的移动，约束力偶限制了法向的两转动。由此可知，3个转动副RE的轴线空间平行，3-(RRR)E(RR)S并联机构的运动模式为2T1R。

当动平台沿、方向移动，动平台的约束螺旋不改变，则运动性质不发生改变；当动平台绕方向转动，约束力线矢依然过转动副RS轴线的交点，且方向平行于对应支链转动副RE副的轴线，即约束力线矢位置关系没有改变，动平台的约束螺旋不改变，则运动性质不发生改变。由此可知，在转动副RE轴线空间平行的布置情况下，3-(RRR)E(RR)S并联机构的运动模式为2T1R，且具有全周性。两平移一转动机构可用于抓放定位操作，在2T1R运动模式下，动平台可在平面内移动，通过绕方向转动调整位姿，满足抓放定位需求。

2.3 3R运动模式分析

在装配时，与动平台连接的3个转动副RE的轴线在空间的位置关系为相错。此时，动平台的3个约束力线矢在空间的位置关系也是相错。在静平台上建立如图9所示坐标系，可以写出约束力分别为：

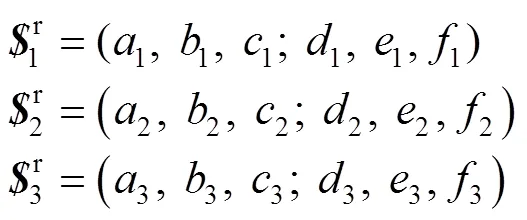
式中：(1，1，1)、(2，2，2)和(3，3，3)为约束力的方向；(1，1，1)、(2，2，2)和(3，3，3)为约束力的线距。

由于动平台受到空间相错三约束力线矢，约束力线矢限制了机构在三维空间的3个方向上的移动。机构只有3个转动自由度，且这3个转动的轴线必须与3个约束力线矢的轴线同时相交。由此可知，3个转动副RE的轴线空间相错，3-(RRR)E(RR)S并联机构的运动模式为3R。

当动平台绕、、方向转动，动平台的约束螺旋不改变，运动性质不发生改变。由此可知，在转动副RE轴线空间相错时，3-(RRR)E(RR)S并联机构的运动模式为3R，且具有全周性。在产品的姿态调整过程中，动平台需要完成3个方向的转动，在3R运动模式下，动平台能够绕、、3个方向转动，可以满足产品空间姿态调整需求。

综上所述，由运动模式分析可知，当与动平台相连的转动副轴线共面不汇交时，机构绕轴、轴转动以及沿轴移动；当与动平台相连的转动副轴线空间平行时，机构沿轴、轴方向移动和绕轴转动；当与动平台相连的转动副轴线空间相错时，机构绕轴、轴和轴转动。3种运动模式下，机构的自由度均具有全周性。当机构处于2R1T运动模式，满足物流分拣需求；当机构处于2T1R运动模式，满足抓放定位需求；当机构处于3R运动模式，满足产品姿态调整需求。

3 结语

1）基于线矢量与偶量的相关性，两平行线矢等效为一线矢和一法向偶量；共面三线式等效为平面两线矢和一法向偶量；空间平行三线式等效为一线矢和两法向偶量。

2）运动支链对动平台的约束力线矢平行或三力线矢共面时，部分约束力等效为法向约束力偶，机构的运动模式发生改变，这为多模式并联机构构型综合提供了理论方法。

3）转动副RE轴线共面不汇交时，3-(RRR)E(RR)S并联机构绕轴、轴转动及沿轴移动，为2R1T运动模式；空间平行时，并联机构沿轴、轴移动和绕轴转动，为2T1R运动模式；空间相错时，并联机构绕轴、轴和轴转动，为3R运动模式。

4）E转动副轴线位置不同时，3-(RRR)E(RR)S并联机构分别处于3R、2T1R和2R1T 3种不同的运动模式，可应用于需求多运动模式的分拣、抓放、调姿的包装生产工程领域。

[1] 康熙, 戴建生. 机构学中机构重构的理论难点与研究进展——变胞机构演变内涵、分岔机理、设计综合及其应用[J]. 中国机械工程, 2020, 31(1): 57-71.

KANG Xi, DAI Jian-sheng. Theoretical Difficulties and Research Progresses of Mechanism Reconfiguration in Mechanisms—Evolution Connotation, Furcation Principle, Design Synthesis and Application of Metamorphic Mechanisms[J]. China Mechanical Engineering, 2020, 31(1): 57-71.

[2] AGOFINO A, SUNSPIRAL V, ATKINSON D. Super Ball Bot-Structures Planetary Landing and Exploration[C]// NASA Innovative Advance Concepts Phase Ⅰ Conference, Chicago, 2013: 1-89.

[3] GUO J, ZHAO Y, XU Y, et al. A Novel Modular Deployable Mechanism for the Truss Antenna: Assembly Principle and Performance Analysis[J]. Aerospace Science and Technology, 2020, 105: 105976.

[4] DING Wan, RUAN Qiang, YAO Yan-an. Design and Locomotion Analysis of a Novel Deformable Mobile Robot with Two Spatial Reconfigurable Platforms and Three Kinematic Chains[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2016, 231(8): 203-210.

[5] 王冰, 方跃法. 一种可重构并联机构的几何约束和自由度分析[J]. 机械工程学报, 2018, 54(7): 28-37.

WANG Bing, FANG Yue-fa. Geometric Constraint and Mobility Analysis of a Reconfigurable Parallel Mechanism[J]. Journal of Mechanical Engineering, 2018, 54(7): 28-37.

[6] REFAAT S, HERVÉ J M, NAHAVANDI S, et al. Two-Mode Overconstrained Three-DOFs Rotational-Translational Linear-Motor-Based Parallel-Kinematics Mechanism for Machine Tool Applications[J]. Robotica, 2007, 25(4): 461-466.

[7] RUGGIU M, KONG Xian-wen. Mobility and Kinematic Analysis of a Parallel Mechanism with both PPR and Planar Operation Modes[J]. Mechanism and Machine Theory, 2012, 55: 77-90.

[8] LUO H, WANG S. Multi-Manipulation with a Metamorphic Instrumental Hand for Robotassisted Minimally Invasive Surgery[C]// Proc. IEEE/ICME International Conference on Complex Medical Engineering, 2011: 260-270.

[9] NURAHMI L, CARO S, SOLICHIN M. A Novel Ankle Rehabilitation Device Based on a Reconfigurable 3-RPS Parallel Manipulator[J]. Mechanism and Machine Theory, 2019, 134: 135-150.

[10] TSENG T, LIN Y, HSU W, et al. A Novel Reconfigurable Gravity Balancer for Lower-Limb Rehabilitation with Switchable Hip/Knee-Only Exercise[J]. Journal of Mechanisms and Robotics, 2017, 9(4): 041002.

[11] FERDINANDO C, DAI J S. Origami-Carton Tuck-in with a Reconfigurable Linkage[C]// ASME/IFToMM International Conference on Reconfigurable Mechanisms and Robots, London, UK, 2009: 512-520.

[12] 陈辉庆. 新型可控变胞式码垛机器人动态可靠性研究[D]. 南宁: 广西大学, 2022: 10-14.

CHEN Hui-qing. Research on Dynamic Reliability of a New Controllable Metamorphic Palletizing Robot[D]. Nanning: Guangxi University, 2022: 10-14.

[13] DAI J S, JONES J R. Mobility in Metamorphic Mechanisms of Foldable/Erectable Kinds[J]. Journal of Mechanical Design, 1999, 121(3): 375-382.

[14] GAN Dong-ming, DAI Jian, LIAO Qi-zheng. Constraint Analysis on Mobility Change of a Novel Metamorphic Parallel Mechanism[J]. Mechanism and Machine Theory, 2010, 45(12): 1864-1876.

[15] 于靖军, 刘凯, 孔宪文. 多模式机构研究进展[J]. 机械工程学报, 2020, 56(19): 14-27.

YU Jing-jun, LIU Kai, KONG Xian-wen. Research Progress of Multi-Mode Mechanism[J]. Journal of Mechanical Engineering, 2020, 56(19): 14-27.

[16] WOHLHART K. Advances in Robot Kinematics[M]. Dordrecht: Kluwer Academic, 1996.

[17] DAI Jian, WANG De-lun, CUI Lei. Orientation and Workspace Analysis of the Multifingered Metamorphic Hand-Metahand[J]. IEEE Transactions on Robotics, 2009, 25(4): 942-947.

[18] 王德伦, 戴建生. 变胞机构及其综合的理论基础[J]. 机械工程学报, 2007, 43(8): 32-42.

WANG De-lun, DAI Jian-sheng. Theoretical Foundation of Metamorphic Mechanism and Its Synthesis[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 32-42.

[19] GAN D M, DAI J S, LIAO Q Z. Mobility Change in Two Types of Metamorphic Parallel Mechanisms[J]. Journal of Mechanisms and Robotics, 2009, 1(4): 1-10.

[20] KONG X, GOSSELIN C, RICHARD P L. Type Synthesis of Parallel Mechanisms with Multiple Operation Modes[J]. Journal of Mechanical Design, 2007, 129(6): 595-601.

[21] FAN C, LIU H, ZHANG Y. Type Synthesis of 2T2R, 1T2R and 2R Parallel Mechanisms[J]. Mechanism and Machine Theory, 2013, 61: 184-190.

[22] LI Qin-chuan, HERVÉ J. Parallel Mechanisms with Bifurcation of Schoenflies Motion[J]. IEEE Transactions on Robotics, 2009, 25(1): 158-164.

[23] 叶伟, 方跃法, 郭盛, 等. 一种新型并联机构的运动分岔特性及运动学分析[J]. 机械工程学报, 2013, 49(13): 8-16.

YE Wei, FANG Yue-fa, GUO Sheng, et al. Bifurcated Motion and Kinematics of Novel Parallel Mechanism[J]. Journal of Mechanical Engineering, 2013, 49(13): 8-16.

[24] 石志新, 叶梅燕, 罗玉峰, 等. 四自由度两模式并联机构结构综合与位置分析[J]. 农业机械学报, 2017, 48(4): 383-389.

SHI Zhi-xin, YE Mei-yan, LUO Yu-feng, et al. Type Synthesis and Position Analysis of 4-DOF Parallel Mechanisms with Two Operation Modes[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(4): 383-389.

[25] 张春燕, 刘香玉, 倪聪, 等. 基于单环运动链的多模式移动机构型综合[J]. 机械传动, 2020, 44(4): 17-25.

ZHANG Chun-yan, LIU Xiang-yu, NI Cong, et al. Type Synthesis of Mobile Mechanisms with Multiple Modes Based on Single-Loop Kinematic Chains[J]. Journal of Mechanical Transmission, 2020, 44(4): 17-25.

[26] CHABLAT D, KONG X, ZHANG C. Kinematics, Workspace, and Singularity Analysis of a Parallel Robot with Five Operation Modes[J]. Journal of Mechanisms and Robotics, 2018, 10(3): 035001.

[27] 黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006.

HUANG Zhen, ZHAO Yong-sheng, ZHAO Tie-shi. Advanced Spatial Mechanism[M]. Beijing: Higher Education Press, 2006.

Analysis of Multi-motion Mode Based on 3-(RRR)E(RR)SParallel Mechanism

SHEN Bo1, GUO Wen-xiao2,3, LI Rui-qin3*

(1. Department of Mechanical and Electrical Engineering, Shanxi Conservancy Technical Institute, Taiyuan 030032, China; 2. China Coal Technology & Engineering Group Taiyuan Research Institute Co., Ltd., Taiyuan 030006, China; 3. School of Mechanical Engineering, North University of China, Taiyuan 030051, China)

The multi-mode robot has the characteristics of intelligent reconfigurable and variable structure, and can actively or passively adapt to the changing environment. The work aims to design a multi-motion mode parallel mechanism that can be applied in the field of packaging engineering. Based on the screw theory, by studying the correlation between the line vector and the couple in different geometric spaces, it was concluded that the constraint force could be transformed into the normal constraint couple under certain conditions, which provided theoretical support for the parallel mechanism to realize multi-mode motion. Through the deformation of the 3-(RRR)E(RR)Sparallel mechanism, it was concluded that the mechanism had three motion modes of 3R, 2T1R and 2R1T, and the degree of freedom was 3 in each motion mode, with full-cycle mobility. Based on the 3-(RRR)E(RR)Sparallel mechanism, the constraint conditions of the mechanism are changed by changing the spatial position relationship of the branch constraint force line vector, so that the parallel mechanism can realize 3R, 2T1R and 2R1T multi-mode motion. It meets the needs of logistics sorting, grasping and positioning, product space attitude adjustment, etc.

multi-motion mode; parallel mechanism; screw theory; degree of freedom

TS206.4

A

1001-3563(2023)19-0205-07

10.19554/j.cnki.1001-3563.2023.19.026

2023-05-15

山西省重点研发计划（201803D421028，201903D421051）

责任编辑：曾钰婵