基于分数阶滑模控制的高精度印刷机纠偏系统研究

陈一军，郭忠旭，武吉梅，邵明月，王静

基于分数阶滑模控制的高精度印刷机纠偏系统研究

陈一军，郭忠旭，武吉梅*，邵明月，王静

（西安理工大学 印刷包装与数字媒体学院，西安 710048）

解决卷对卷印刷收卷不齐的问题，提高收卷精度。对印刷机收卷纠偏原理进行分析，建立收卷纠偏系统数学模型，提出基于分数阶滑模控制的纠偏算法，分析其稳定性。在不同收卷线速度、不同跑偏干扰输入信号的条件下进行仿真。搭建收卷纠偏实验平台，对2种控制方法进行收卷纠偏控制实验。仿真结果表明，分数阶滑模控制器比传统PID控制器具有较好的动态性能和稳态性能。实验结果表明，分数阶滑模控制算法比传统PID控制具有更高的纠偏精度。分数阶滑模控制算法可以有效提高印刷机收卷纠偏精度，满足高精度印刷要求。

纠偏；分数阶滑模控制；收卷控制；MATLAB仿真

卷对卷印刷在印刷行业具有广泛的应用，印刷机在收卷过程中，由于卷材的张力变化、两段料卷拼接不齐，以及卷材的厚度不均匀等因素的影响，呈现出交替随机的横向偏移。这种现象会造成收卷时边缘不整齐，影响印品质量[1]。为此，目前印刷机通常配有收卷纠偏系统[2]。

印刷机收卷纠偏系统由于工作环境复杂，所以存在诸多不利于控制系统设计的影响因素，如非线性因素、外部干扰因素、收卷轴负载变化等。由于收卷纠偏系统具有多种干扰因素的影响，使得传统PID控制器难以提高其控制性能。在“中国制造2025”背景下，智能控制策略发展迅速，新型控制策略在传统制造业上应用越来越多。因此，在收卷纠偏控制系统设计时解决被控对象干扰因素多、不确定性强的问题具有一定的理论和工程实际意义。

相较于其他控制方法，滑模控制算法具有很多优点。如对参数摄动具有不敏感性、对不确定性外部扰动具鲁棒性强等特点，因此滑模控制算法具有广泛的应用[3]。但滑模控制因为其系统的执行时切换开关，使其具有一定的滞后性，滑模面上的滑动模态不能准确发生，造成系统抖振。分数阶系统具有能量传递及收敛速度缓慢的特点，在滑膜控制器的设计中加入分数阶理论能够有效地降低滑模控制的抖振幅度及频率，可以有效减弱系统的抖振，减少调节时间，降低系统的能量损耗，并且具有较好的鲁棒性[4]。

1 收卷纠偏工作原理

印刷机收卷纠偏系统是利用超声波传感器对卷材进行边缘检测，检测到卷材与设定值发生横向偏移时，将检测到的偏移信号作为系统的输入信号，传输到纠偏控制器中，控制器比较检测到偏移信号与设定偏移量，产生偏差信号，并将该信号转换成脉冲量传递给步进电机驱动器，由步进电机带动纠偏执行机构完成纠偏动作，上述过程反复进行，形成闭环控制，直至偏差信号为0。凹版印刷机收卷纠偏系统的结构原理简图如图1所示[5]。

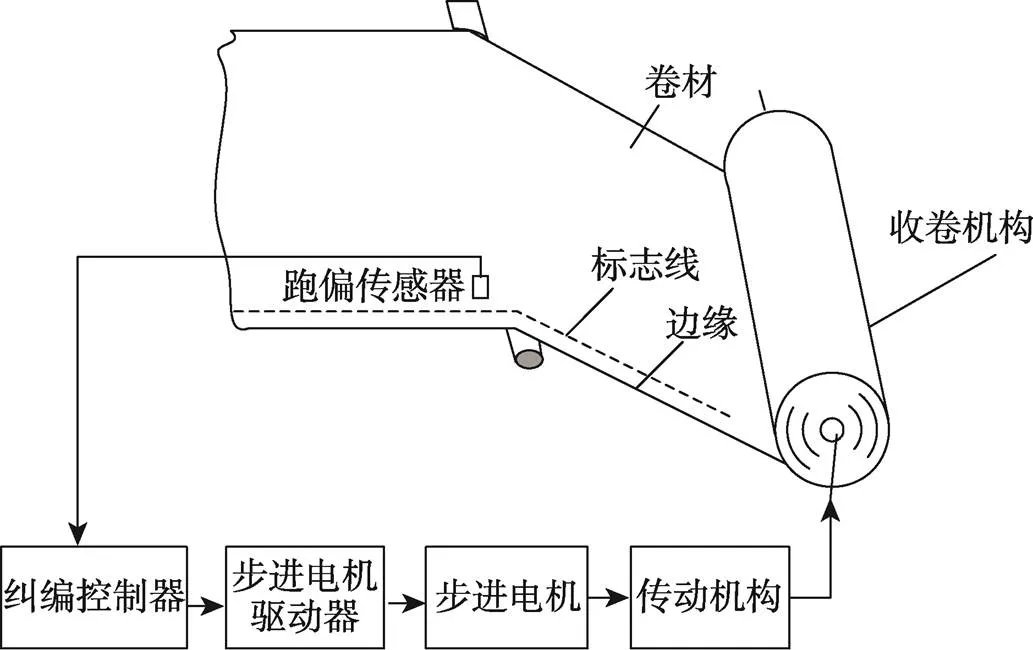
图1 卷筒纸印刷收卷纠偏系统结构

2 收卷纠偏系统数学模型

收卷纠偏系统的数学模型见图2。

图2 印刷机收卷纠偏控制系统的数学模型

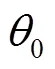
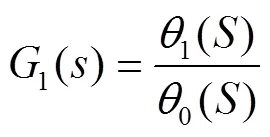
步进电机两相励磁电压平衡方程可以表示为式（2）。

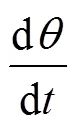
步进电机转子力矩平衡方程分别表示为：

式中：e为电磁转矩；L为负载转矩；为总转动惯量；为黏滞摩擦因数。

由式（3）可得步进电机的机械运动方程：

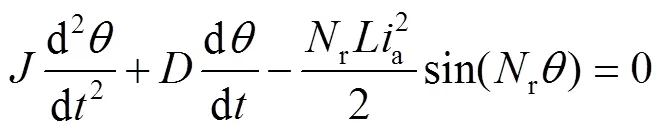
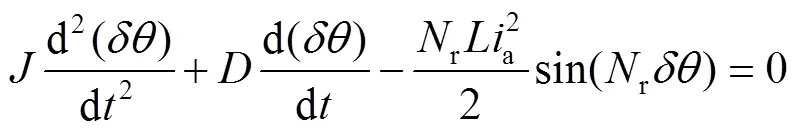
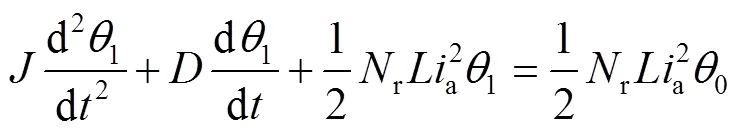
作拉普拉斯变换，将初值0代入可得：

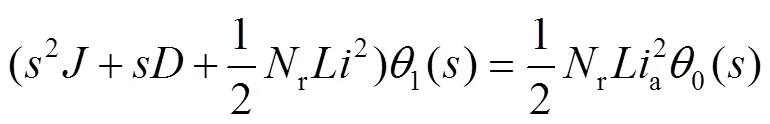
可得步进电机的传递函数数学模型为：

对于纠偏系统的传动部分，是由步进电机驱动滑动丝杠机构，将旋转运动转换成横向运动，其传递函数为：

卷材偏移检测处到收卷轴上的传输通道传递函数：

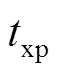
系统的开环传递函数见式（11）。

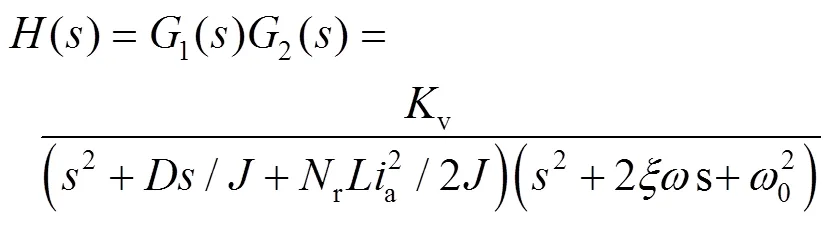
根据系统开环传递函数，绘制系统伯德图，见图3。

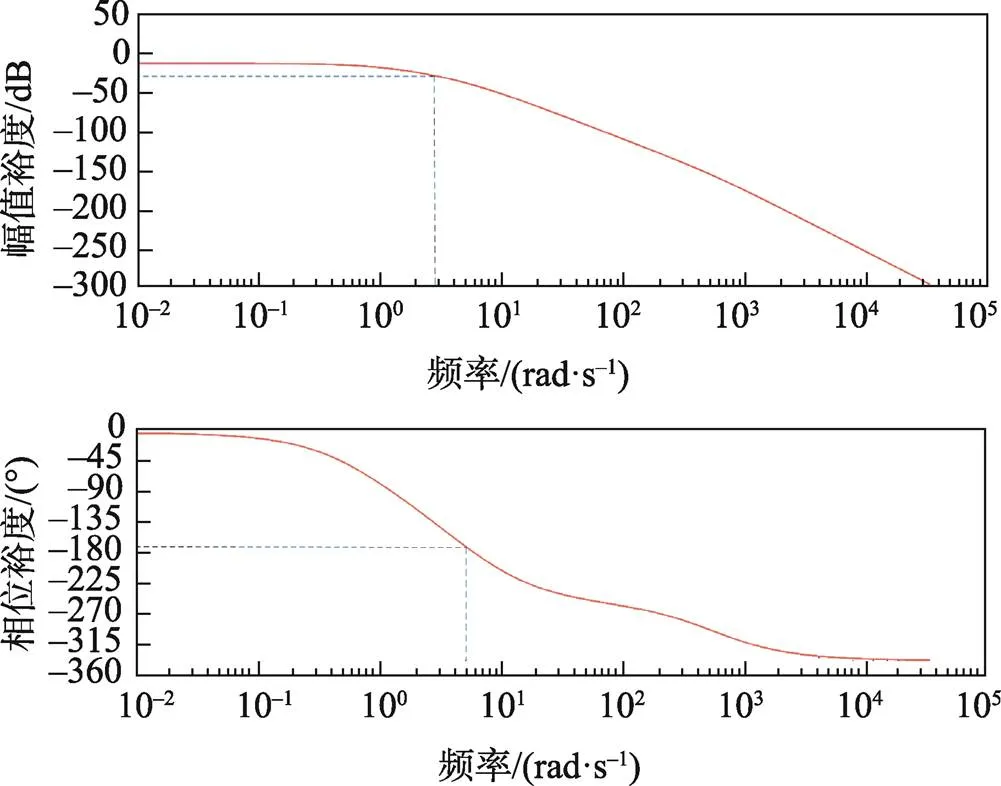
图3 系统伯德图

开环伯德图如图3所示，截止频率i为8 rad/s，相频截止频率g为8.02 rad/s，相位裕度为52°，幅值裕度为10 dB，系统稳定符合工程上一般要求。

3 分数阶滑模控制器设计

将滑模变结构控制与分数阶理论结合，首先设计分数阶滑模面。首先通过添加分数阶微分项增加了滑膜控制的灵活性，对滑模控制易于出现的抖振问题能够有效抑制；然后设计分数阶滑模控制的趋近率，使系统能够稳定在分数阶滑模面后保持滑模运动，且具有较小的稳态误差；最后通过李雅普诺夫理论验证分数阶滑模控制器的稳定性[7]。

以步进电机为系统控制对象设计跟踪误差系统，结合步进电机的机械运动方程可以设计为式（12）[8]。

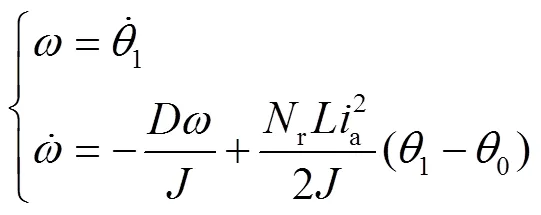
对式（13）求导可以得：

分数阶滑模面可以设计为：

为了满足滑模条件，设计如下趋近率，其表达式见式（2）。

式中：1和2为滑模增益，1>0，2>0。

对滑模面进行求导：

定义1=、2=，式（16）可以写为：

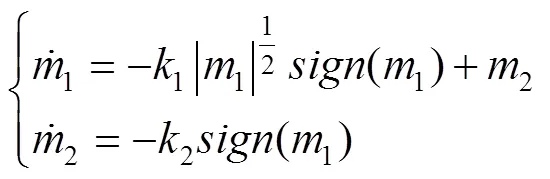
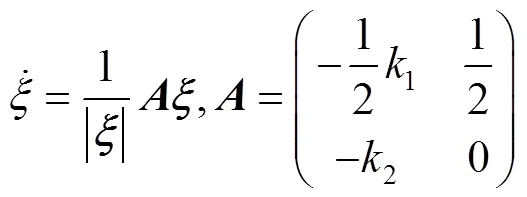
基于李雅普诺夫（Lyapunov）理论证明分数阶滑模控制的稳定性。现构建如下李雅普诺夫函数[9]：

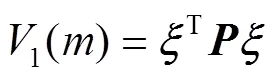
其中：

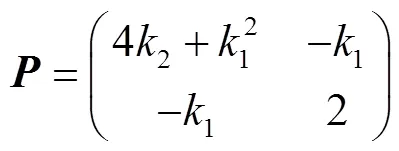
为了使Lyapunov函数为正定，只要保证矩阵为正定即可。显然，只要满足矩阵中2>0，矩阵总是正定的。所以1()满足以下不等式：

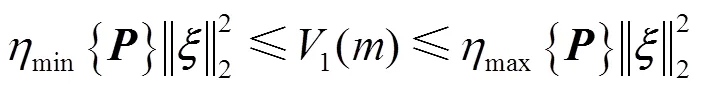
则有：

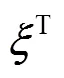
根据式（22）、式（25）可以得出结论：

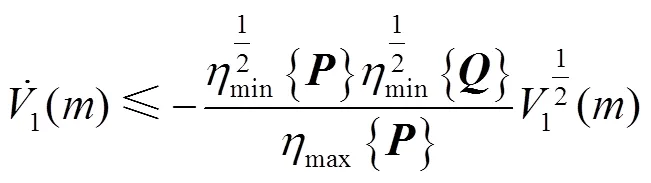
令：

则式（27）可以表示为：

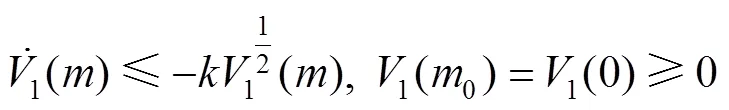
式中：1(0)表示Lyapunov函数的初始值。因为>0，所以收敛时间计算如下：

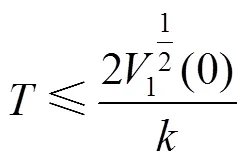
结合式（25）和式（30），根据Lyapunov稳定性理论可知本文所提出的分数阶滑模控制算法是稳定的，且收敛时间有限。

4 仿真分析

为了验证所提出的分数阶滑模控制对印刷机收卷纠偏的效果，利用MATLAB/Simulink对其进行仿真实验，并将分数阶滑模控制算法与传统PID控制进行性能比较。首先基于图4所搭建的仿真模型[9]，在仿真模型中设置阶跃、正弦和多频正弦3种干扰信号模拟不同工况下的系统抗干扰情况[10]。本次仿真还依据式（10）中卷材偏移检测处到收卷轴上的传输通道传递函数中关于速度对跑偏信号的影响，设置不同收卷线速度对纠偏情况进行仿真[11-12]。

图4 基于分数阶滑模控制系统的 Simulink模型

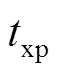
在不同线速度、不同跑偏信号的条件下，收卷纠偏控制系统的动、静态性能数据如表1所示。

根据系统仿真图和2种控制方式仿真结果表可知，在不同线速度及不同干扰跑偏信号下基于分数及滑模控制的纠偏控制方案较传统PID控制具有更小的动态误差和稳态误差，纠偏效果得到明显提升。

5 实验分析

选用改进的陕西北人印刷机械有限公司FR-400机组式凹版印刷机作为实验平台，设计加装了收卷纠偏机构，如图8所示。纠偏电机选用力川LCDA86H闭环步进电机，直流60 V供电，其定位精度较高；跑偏传感器选用精科US-400S超声波传感器，具有较高的检测精度；卷材选用幅宽为600 mm PET薄膜，其具有较好的柔韧性，可减小因张力过大造成薄膜变形对跑偏的影响。

图5 阶跃信号干扰下PID控制与分数阶滑模控制抗干扰效果对比

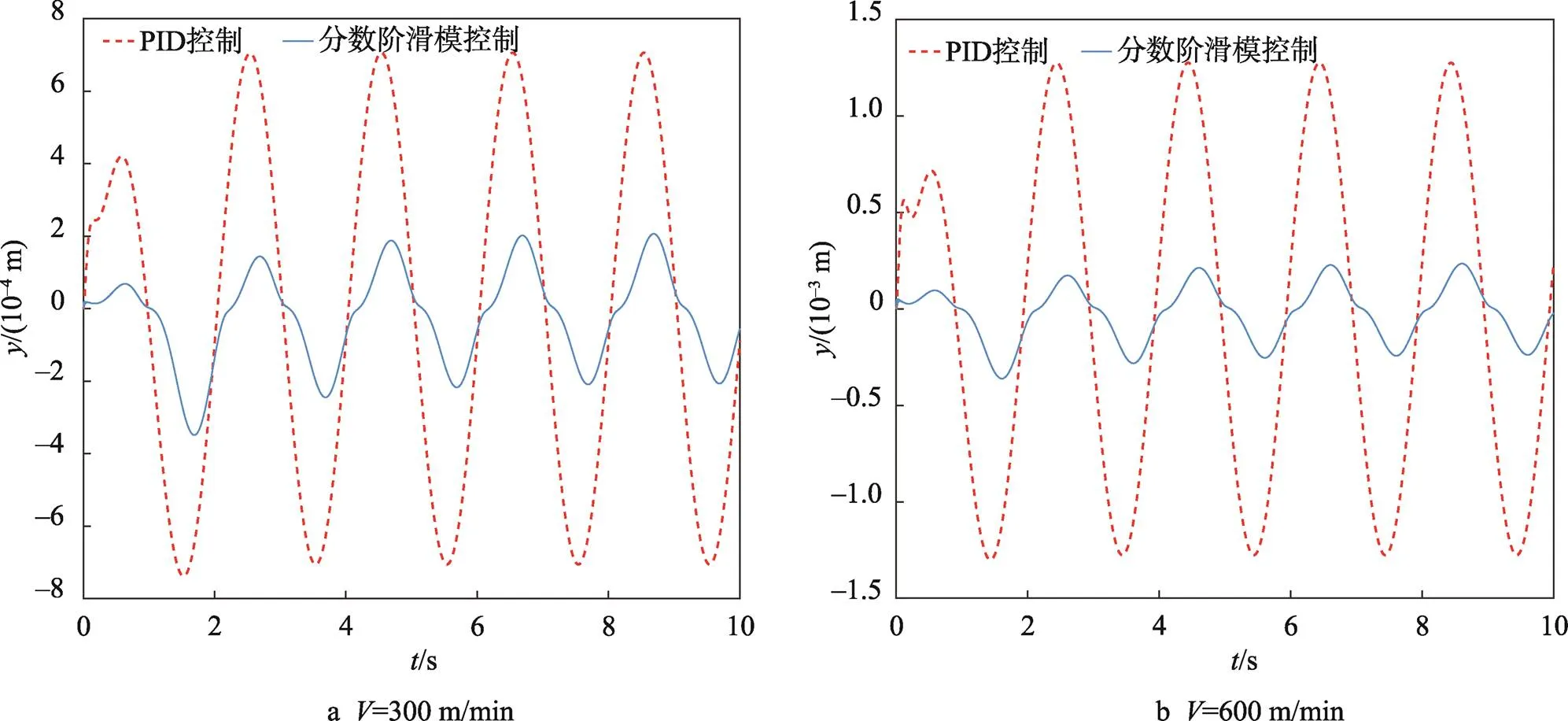
图6 正弦信号干扰下PID控制与分数阶滑模控制抗干扰效果对比

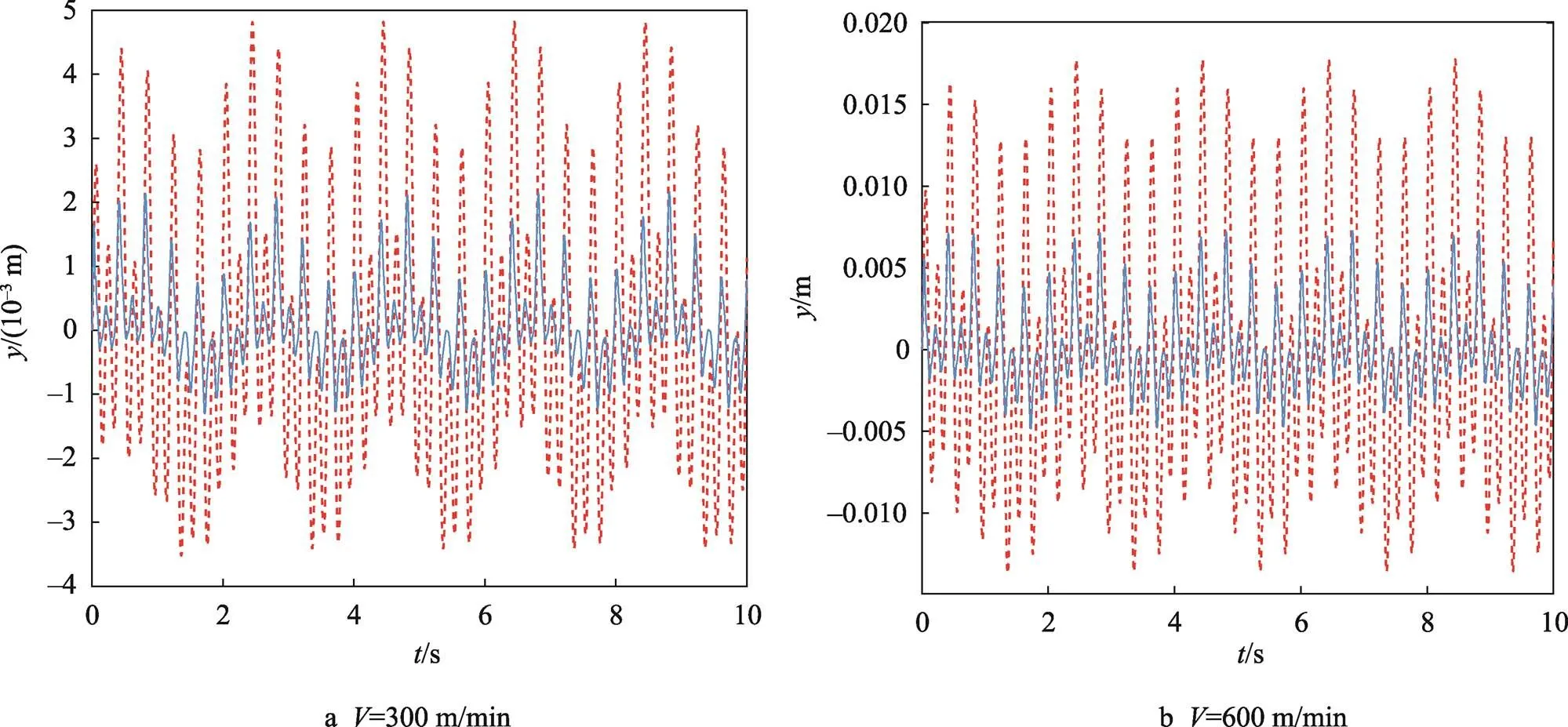
图7 多频正弦信号干扰下PID控制与分数阶滑模控制抗干扰效果对比

表1 在不同线速度和跑偏输入信号条件下收卷系统的动、静态性能对比

Tab.1 Dynamic and static performance of the winding system under conditions of different sets of different line speeds and different off-track input signals

图8 收卷纠偏控制系统实验平台

为了验证分数阶滑模控制系统的纠偏效果，以超声波传感器中心位置为基准，设置坐标偏移量为5 mm，设置收卷线速度为150 r/min，测试传统PID控制及分数阶滑模控制纠偏控制绝对误差，系统流程控制框图如图9所示，测试所得结果如表2所示。

由表2数据可以看出，传统PID控制纠偏绝对误差最大值为0.32 mm，平均值为0.24 mm；分数阶滑模控制纠偏绝对误差最大值为0.16 mm，平均值为0.15 mm，满足印刷工艺要求。通过实验数据分析可知分数阶滑模纠偏控制纠偏效果的绝对误差最大值及平均值均低于传统PID控制的相应值，因此，分数阶滑模控制可以有效提升纠偏控制精度。

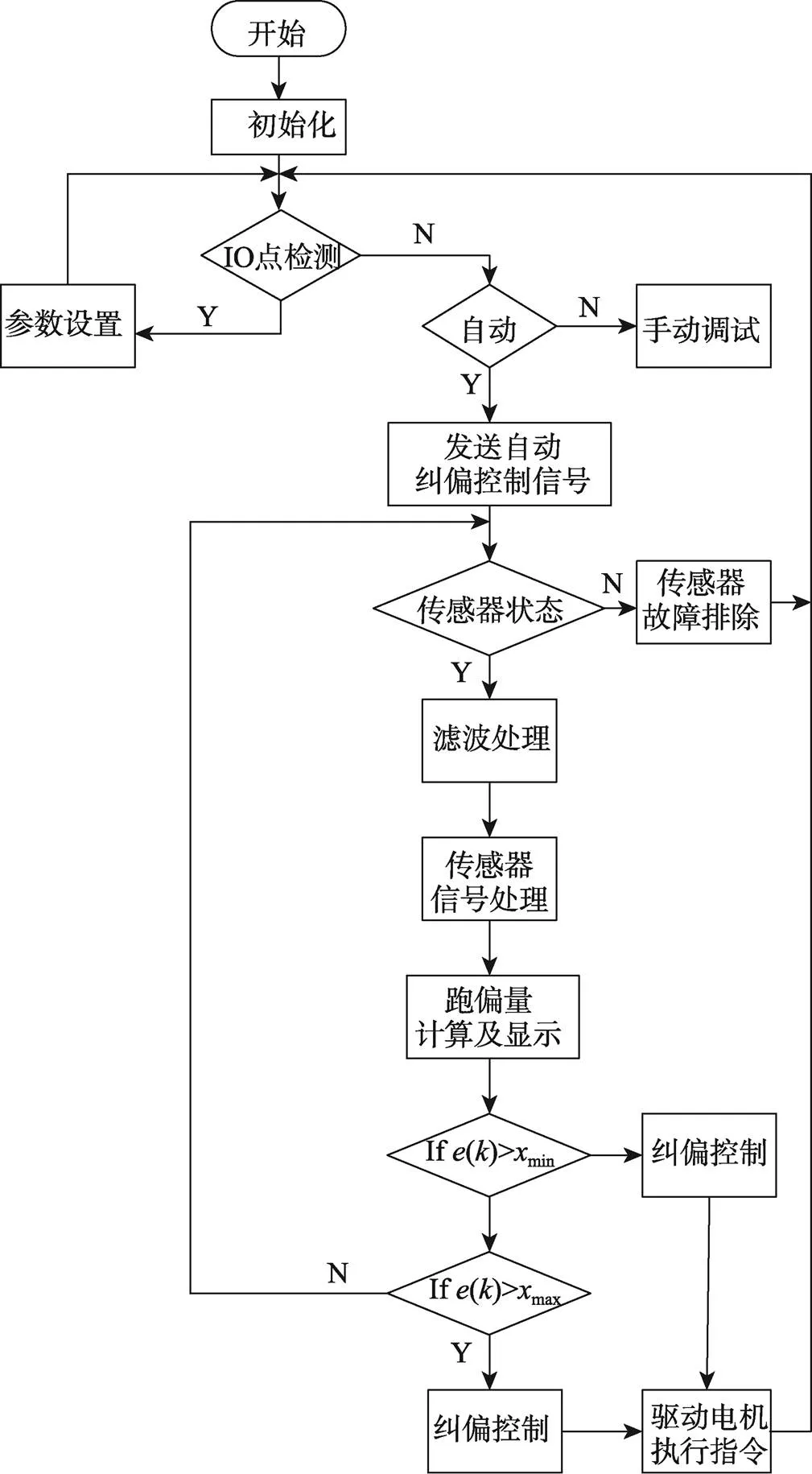
图9 收卷纠偏系统控制系统流程

表2 纠偏效果数据

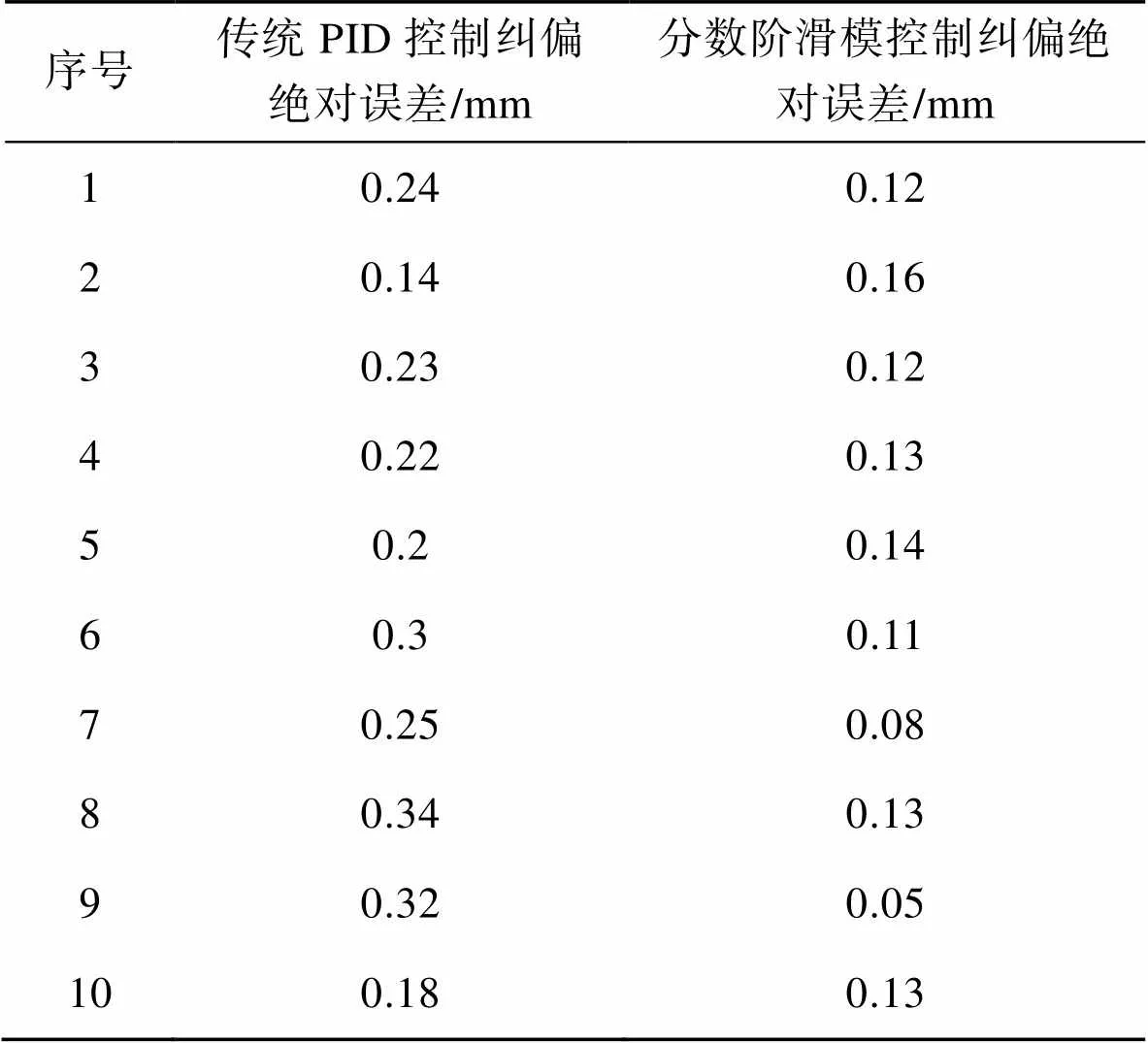
Tab.2 Data of guiding effect

6 结语

文中设计了一种基于分数阶滑模控制的印刷机收卷纠偏控制器，用于解决卷对卷印刷中收卷不齐的问题[15]。利用李雅普诺夫理论证明了分数阶滑模控制算法稳定性；在多速度多干扰的情况下，将所设计的分数阶滑模控制算法与传统PID算法进行仿真对比，得到分数阶滑模控制具有较高的抗干扰性能、较高的控制精度、较强的鲁棒性。搭建了实验平台，进行了纠偏效果对比实验，实验表明分数阶滑模控制具有更好的纠偏效果，可以有效提高印刷机的收卷纠偏精度，对实际印刷生产具有重要意义。

[1] 武秋敏，武吉梅. 印刷设备[M]. 北京: 中国轻工业出版社, 2018: 1-20.

WU Qiu-min, WU Ji-mei. Printing Equipment[M]. Beijing: China Light Industry Press, 2018: 1-20.

[2] ZHOU C, SONG Z K. Application of Ultrasonic in Web Guiding System[J]. Instrumentation Technology, 2010(9): 40-41.

[3] 白淏文, 韩光信. 分数阶滑模控制算法在四容水箱中的应用及仿真[J]. 吉林化工学院学报, 2021, 38(7): 13-17.

BAI Hao-wen, HAN Guang-xin. Application and Simulation of Fractional-Order Sliding Mode Control Algorithm in Four-Tank[J]. Journal of Jilin Institute of Chemical Technology, 2021, 38(7): 13-17.

[4] 黄道敏, 韩丽君, 唐国元, 等. 水下机械手分数阶积分滑模轨迹跟踪控制方法研究[J]. 中国机械工程, 2019, 30(13): 1513-1518.

HUANG Dao-min, HAN Li-jun, TANG Guo-yuan, et al. Fractional Integral Sliding Mode Control for Trajectory Tracking of Underwater Manipulators[J]. China Mechanical Engineering, 2019, 30(13): 1513-1518.

[5] NESKA M, MAJCHER A. System for Automatic Web Guiding for Roll-to-Roll Machine Working in a Start-Stop Mode[J]. Solid State Phenomena, 2015, 223: 374-382.

[6] 邓瑞, 侯和平, 徐卓飞, 等. 印刷纸带纠偏装置研究与系统开发[J]. 包装工程, 2018, 39(13): 138-143.

DENG Rui, HOU He-ping, XU Zhuo-fei, et al. Research on the Guiding Control Device of Printing Paper Tape and System Development[J]. Packaging Engineering, 2018, 39(13): 138-143.

[7] MAO Bei-xing. Two Methods for Terminal Sliding-Mode Synchronization of Fractional-Order Nonlinear Chaotic Systems[J].Asian Journal of Control, 2021, 23: 1720-1727.

[8] 张建宇, 高天宇, 于潇雁, 等. 基于自适应时延估计的空间机械臂连续非奇异终端滑模控制[J]. 机械工程学报, 2021, 57(11): 177-183.

ZHANG Jian-yu, GAO Tian-yu, YU Xiao-yan, et al. Continuous Non-Singular Terminal Sliding Mode Control of Space Robot Based on Adaptive Time Delay Estimation[J]. Journal of Mechanical Engineering, 2021, 57(11): 177-183.

[9] 陈大洋, 李章承, 唐立军, 等. 全数字闭环石英挠性加速度计系统校正与仿真[J]. 电子测试, 2020(6): 20-23.

CHEN Da-yang, LI Zhang-cheng, TANG Li-jun, et al. Calibration and Simulation of Full Digital Closed-Loop Shi Ying Flexible Accelerometer System[J]. Electronic Test, 2020(6): 20-23.

[10] 杜恩祥, 王双龙, 常雷. 带前馈补偿的弹标轨迹变论域模糊控制器设计[J]. 装甲兵工程学院学报, 2017, 31(2): 84-89.

DU En-xiang, WANG Shuang-long, CHANG Lei. Variable Universe Fuzzy Controller Design of Missile Mark Trajectory with Feed-Forward Compensation[J]. Journal of Academy of Armored Force Engineering, 2017, 31(2): 84-89.

[11] 赵志诚, 赵志涛, 张井岗, 等. 直流调速系统的改进型分数阶滑模控制[J]. 系统仿真学报, 2018, 30(3): 1096-1101.

ZHAO Zhi-cheng, ZHAO Zhi-tao, ZHANG Jing-gang, et al. Modified Fractional Order Sliding Model Control for DC Speed Regulating System[J]. Journal of System Simulation, 2018, 30(3): 1096-1101.

[12] 李俊泓, 魏振兴. 基于IMC-ESO的电机调速系统抑制干扰方法研究[J]. 电气传动, 2021, 51(23): 3-9.

LI Jun-hong, WEI Zhen-xing. Research on Disturbance Suppression Method of PMSM Speed-Adjusting System Based on IMC-ESO[J]. Electric Drive, 2021, 51(23): 3-9.

[13] 杨芳, 张宽桥, 余磊. 自适应非奇异快速终端二阶滑模制导律[J]. 弹道学报, 2020, 32(2): 7-15.

YANG Fang, ZHANG Kuan-qiao, YU Lei. Adaptive Nonsingular Fast Terminal Second-Order Sliding Mode Guidance Law[J]. Journal of Ballistics, 2020, 32(2): 7-15.

[14] 张培娟. 对带材收卷过程中正弦式跑偏的跟踪控制[D]. 杭州: 杭州电子科技大学, 2013: 30-50.

ZHANG Pei-juan. Tracking Control of Sinusoidal Running Deviation in Strip Winding Process[D]. Hangzhou: Hangzhou Dianzi University, 2013: 30-50.

[15] 黄蒙. 薄膜卷材纠偏控制系统设计与研究[D]. 武汉: 武汉理工大学, 2013: 40-45.

HUANG Meng. Design and Research of Thin Film Membrane Guiding Control System[D]. Wuhan University of Technology, 2013: 40-45.

High-precision Printing Press Guiding System Based on Fractional-order Sliding Mode Control

CHEN Yi-jun,GUO Zhong-xu,WU Ji-mei*,SHAO Ming-yue,WANG Jing

(School of Printing, Packaging Engineering and Digital Media Technology, Xi'an University of Technology, Xi'an 710048, China)

The work aims to solve the problem of uneven roll-to-roll printing, and improve the winding accuracy. The principle of winding and guiding of printing press was analyzed. The mathematical model of winding and guiding systems was established. A correction algorithm based on fractional-order sliding mode control was proposed to analyze its stability. Simulation was carried out under the condition of setting different winding line speeds and different misalignment interference input signals. An experiment platform of winding and guiding was established to conduct winding and guiding experiments on the two control methods. The simulation results showed that fractional-order sliding mode controllers had better dynamic performance and steady-state performance than traditional PID controllers. The experimental results showed that the fractional-order sliding mode control algorithm had higher guiding accuracy than traditional PID controllers. In conclusion, the fractional-order sliding mode control algorithm can effectively improve the winding and guiding accuracy of the printing press and meet the requirements of high-precision printing.

guiding; fractional-order sliding mode control; winding control; MATLAB simulation

TP273

A

1001-3563(2023)19-0171-08

10.19554/j.cnki.1001-3563.2023.19.022

2022-10-28

国家自然科学基金面上项目（52075435，52205127）；陕西省自然科学基础研究计划重点项目（2022JZ-30）；国家新闻出版署智能与绿色柔版印刷重点实验室招标课题（ZBKT202105）

责任编辑：曾钰婵