Frenet坐标框架下的自适应避障算法

匡军，尤杰，钟晓婉，万仁卓，韩冬桂，燕怒*

Frenet坐标框架下的自适应避障算法

匡军1a，尤杰1b，钟晓婉2，万仁卓1b，韩冬桂1a，燕怒1a*

（1.武汉纺织大学 a.机械工程与自动化学院 b.电子与电气工程学院，武汉 430200； 2.襄阳汽车职业技术学院 智能制造学院，湖北 襄阳 441021）

解决包装车间无人运输车辆在沿全局路径行驶过程中，难以同时保证跟随轨迹平滑及规避障碍物的问题。构建Frenet坐标框架，描述车辆位姿与全局路径的相对关系，利用五次多项式生成多条待选局部路径；采用障碍物势场法模糊处理包装车间障碍的外形轮廓，并设置膨胀区间；结合待选路径采样点经过障碍物膨胀区间得到的碰撞值，以及采样点与全局规划路径的偏差值，综合评估路径的避障能力，筛选出最优的避障路径。该算法能根据障碍物的大小，动态解算出与全局路径偏移量小且运动连贯的局部避障路径。所提算法使得车辆完成运输任务时的效果更好，且效率更高。

局部路径规划；避障算法；最优路径；Frenet坐标系；自适应

随着人工智能、计算机技术的迅猛发展，路径规划作为无人运输车辆的核心决策部分，是否具备避障功能是车辆能否安全行驶的关键，也是无人运输技术能否落地实现的前提[1]。局部路径规划能根据车体所处运动状态进行实时动态规划，在面对障碍时车体会及时做出决策响应，因此车辆避障时的局部路径规划是无人运输车辆必须解决的问题之一[2]。

近年来，国内外已有大量学者研究了局部路径规划的相关算法[3–9]。赵明等[4]通过改进的人工势场法，帮助移动机器人快速到达目标点，避免机器人停滞在叠加势场的局部稳定点上而无法移动。针对无轨胶轮车井下路径规划问题，鲍久圣等[10]利用改进的A*算法，提高了节点搜索效率，加快了路径规划时间。虽然上述算法能合理地求解最优的局部路径，并且优化算法模型，减少计算量，但此类算法的求解路线均以离散点的形式连接而成，对车辆实时运动状态连贯性的反应较模糊。魏民祥等[11]以自动驾驶汽车为研究对象，基于Frenet坐标系算法模型，以核心安全指标构建损失函数，求解出更加平滑的运动轨迹。Eshtehardian等[12]提出了一种基于RRT*和b样条相结合的方法，可以平滑快速随机采样点路径，使局部路径规划连贯。Durakl等[13]针对路径规划中过多节点和尖点问题，利用贝塞尔曲线修剪，丢弃多余的节点，并对峰值进行处理，使得轨迹连续平滑。在有障碍物的情况下，面对不同的障碍，针对车辆动态作出运动决策变更的局部路径规划算法的研究较少，其主要原因在于障碍物的空间位置不同且形状、大小各异，极大地影响了车辆跟随全局参考路径行驶轨迹的连贯性，会产生停滞或者转动角加速度过大等情况[2,14]。由此可见，亟须一种能够使车辆平滑跟随全局路径且具备避障能力的算法，以控制车辆按照规划路径行驶。

文中基于Frenet坐标框架，明确车辆位姿与全局路径的相对位置关系，并将控制量引入局部路径规划中，结合路径采样点经过障碍物膨胀区间得到的碰撞总值和全局路径离散点偏差总值，综合评估路径的避障质量，从而筛选出最优局部路径，并反馈到运动规划中，控制车辆的行驶，使无人运输车辆按照规划路径行驶且具备自主避障能力。

1 静态地图信息

此算法模型中的静态地图信息包含全局路径规划和障碍物信息预设。全局路径规划指在包含障碍物的区域内，找到一条从初始点到指定目标点的路径[11]。为了更易表达车体的实时位置及运动状态，通常在笛卡尔坐标系中构建地图场景。在实际规划过程中，由于存在系统误差和躲避障碍物的需求，局部路径与全局路径之间必然存在偏差。由此，这里提出在Frenet坐标框架下，依据全局路径将车体运动状态分解为横向距离和纵向偏差，2个方向相互垂直，更易表达局部路径与全局规划路径的相对关系，从而方便规划局部路径，缩短与全局路径的纵向偏差[15]。为了较好地处理车辆与障碍物的位置关系，解决障碍形状轮廓在局部路径规划中难以表达的难题，将针对地图场景中的障碍物进行膨胀预处理。

文献[2]构建了障碍物的代价势场，模糊处理了障碍物的形状轮廓，并证明了它在局部路径规划中的有效性。基于此，针对包装车间车辆运输的环境，车辆需要绕行的障碍多为阵列的方形，但大小和轮廓不一，因此这里以方形障碍末端位置为圆心，根据轮廓大小设置半径向四周膨胀，建立膨胀区域。障碍物经膨胀处理前后车辆运行轨迹的变更如图1所示。

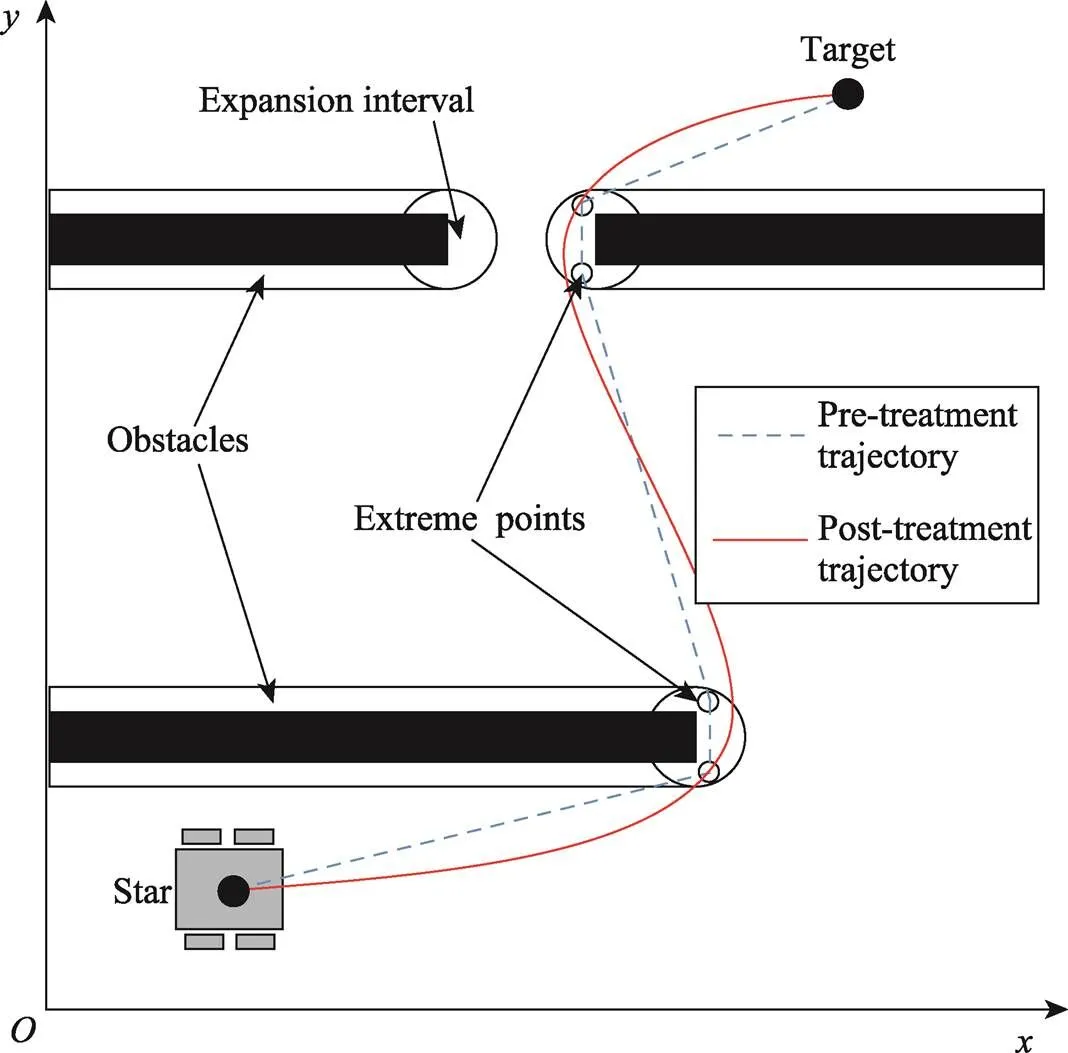
图1 轨迹变更示意图

在图1中，虚线为障碍物膨胀处理前车辆的运行轨迹；实线为障碍物膨胀处理后行驶的轨迹；虚线显示车辆绕行方形障碍时出现了极值，导致车辆运行不平滑，出现速度和转动变化过大的情况。确定障碍物膨胀区间有利于求解局部路径的碰撞值。

2 车体位姿坐标系转化模型

在Frenent框架下规划局部路径，需将在笛卡尔坐标系中的车辆位姿转化到Frenet坐标框架中。构建转化模型，描述车体位姿运动状态，如图2所示。

图2 车体位姿相对关系的描述

如图2所示，由起始点s和终止点t规划全局路径，在平面笛卡尔坐标下，车辆实时位姿数学变量的计算见式（1）。

式中：x、x为车辆在笛卡尔坐标系中的横、纵坐标;v为车辆行驶的速度；为车辆行驶的加速度；θ为行驶偏航角；为角加速度。

在Frenet坐标框架下设置车辆的位姿f状态，见式（2）。

建立数学转换模型，车辆载体坐标系对应的笛卡尔坐标为(x,x)。为车辆对全局路径的投影点，对应的笛卡尔坐标为(r,r)。令向量、向量为平面全局坐标系下正交单位向量；向量、向量为处相互正交的单位向量；向量r、向量r为r处相互正交的单位向量；θ为向量与轴正向的夹角，表示车辆实时位姿角度；r为向量r与轴正向的夹角，表示车辆规划位姿角度；∆为车辆实时位姿角度与规划位姿角度的偏差。通过公式推导可得笛卡尔坐标与Frenet坐标的数学转化模型，见式（3）—（5）。

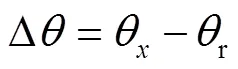
3 最优轨迹筛选策略

最优轨迹筛选策略由2个部分组成。第1部分，将获取车辆的实时位姿，由式（3）—（5）转化至Frenet坐标框架中，获得与全局规划路径纵向偏差和横向位移的相对关系，并以此作为起始状态点。然后根据需求在纵向（偏差）和横向（位移）上，分别规划多个终止状态点，以五次多项式的形式，求解多条随时间变化的曲线。针对车辆的运动状态，构建损失函数，以相应权重来计算2个方向耦合得到的轨迹质量，并设置轨迹质量阈值，初步筛选出满足规划要求的局部路径集合。第2部分，将Frenet框架下耦合得到的局部规划路径集合，反馈到笛卡尔坐标系中，得到多条笛卡尔坐标系中的局部规划路径，并从2个维度对生成的轨迹进行评估。第1个维度从安全性角度出发，根据地图中的障碍信息，计算每条待选轨迹的碰撞总值。第2个维度从跟随效果出发，计算轨迹采样点与全局规划路径的偏差，得到每条待选轨迹的偏差总值。权衡求解出偏差较小且安全性较高的最优跟随轨迹。最后，依据该路径曲线求解出采样间隔时间∆后的车辆位姿，进而控制车辆平滑行驶至该规划点，实现最优局部跟随。为了保证路径的平滑，将以此规划点作为下次规划点的初始状态点，循环往复，直至车辆到达目标点，从而完成全局路径跟随。

3.1 Frenet框架下局部路径规划

为了保证运动状态连贯且平滑，依据Frenet框架中的Jerk模型，可将车辆位姿随时间变化的横向距离和纵向偏差用五次多项式拟合为曲线，表示时刻，见式（6）。

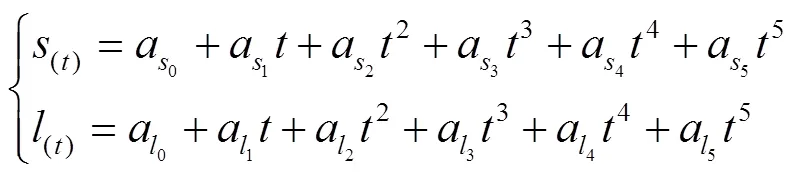
通过规划Frenet坐标横向距离f和纵向偏差f的初始状态和终止状态，可求解a与a各系数的值，见式（7）—（9）。

针对纵向偏差f，根据车辆大小和全局路径宽度，可将终止状态点与全局路径偏差(e)控制在[−, +]距离区间内，负号表示规划局部轨迹穿过规划全局路径，正号表示未穿过，并通过设置∆为等间距偏差，来控制待选路径的数量密度。终止点运动状态与全局规划路径切向同向，因此l(e)和l(e)为0，由式（9）可规划得到种纵向偏差f随时间变化的曲线。

同样需要规划横向距离f的终止点，在一定范围内动态设置s(e)和s(e)，满足车辆行驶过程中的速度需求。将式（7）—（8）代入式（6），得到规划曲线集合。

由于车辆局部运动速度和加速度规划往往会影响车辆运动状态的连贯性，并且面对载人车辆，该规划直接影响乘坐人员的舒适程度[11]。基于此，将2个方向规划的曲线，以时间间隔∆离散为个采样点。根据曲线加速度、加速度变化率等信息构建损失函数，并以相应权重计算路径质量，见式（10）—（12）。

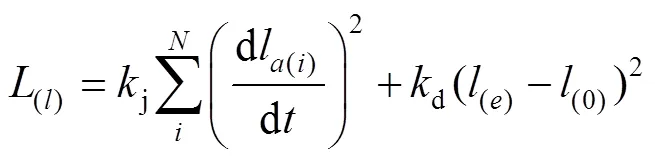
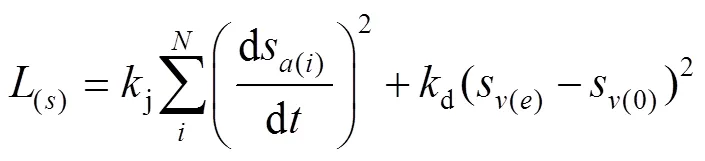
式中：(l)、(s)分别为纵向损失函数和横向损失函数；j、d为比例系数；k、k为2个方向上的加权系数，它们分别控制横向维度和纵向维度对局部轨迹规划的影响；为该局部轨迹的综合得分，以此来评估该轨迹的优劣情况，通过设置阈值，筛选出多条符合预期的待选局部轨迹曲线。

3.2 求解最优局部避障轨迹

如图3所示，无箭头实线表示车辆需跟随的全局规划路径，有箭头的实线为局部待选轨迹集合，并将其中的轨迹4用虚线表示，便于描述算法的处理方式，曲线上实心圆为采样点。为单个轨迹采样点的偏差距离，为单个采样点到附近障碍物的距离，为附近障碍物的膨胀半径。如图3中轨迹4所示，将局部轨迹离散为多个采样点坐标(li,li)，与之对应的全局路径离散点坐标为(gi,gi)，障碍物的膨胀区域圆心坐标为(d,d)，并根据式（13）—（17）分别计算路径的评估质量。

图3 碰撞总值和偏差总值的计算模型

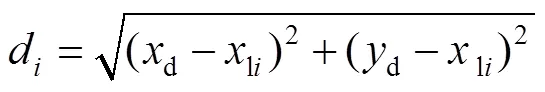
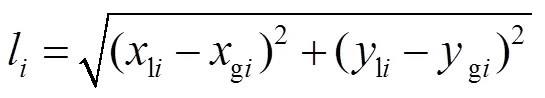
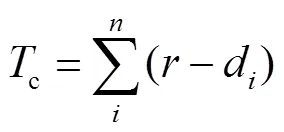
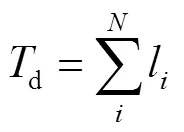
将式（13）代入式（15）中，求得该路径的碰撞总值c，根据前面障碍物地图设置中所述，表示处于障碍物膨胀区域内的离散点数量，障碍物膨胀区域外离散点碰撞值为0。将式（14）代入式（16）中，可以求得路径的偏差总值d，表示该局部路径离散采样点的总数量。最后由式（17）计算出从2个维度综合得到的路径评估值V。1、2为比例系数。不难发现，当c较小时，车辆局部轨迹远离障碍物，安全性较高。当d较小时，车辆局部运动轨迹与全局规划路径偏差较小。由此可见，V最小的曲线为最优避障曲线，能使局部路径在规避障碍的同时，与全局规划路径的偏移量最小。

4 实验分析

4.1 系统实验平台搭建

为了验证该算法的可行性，这里搭建了一辆以STM32F103芯片为底层驱动板的四轮小车，以STM32F407芯片为核心控制板，用以写入算法。在实验初始过程，由起始出发点和终止目标点生成全局路径，将障碍物的位置、大小、形状通过膨胀算法处理，生成静态地图，并赋值到芯片处理系统中，以校准小车起始点位姿。在实验过程中，通过搭载MEMS-INS/GNSS北斗导航系统获取车体的实时位姿数据，用以观测车辆的行驶情况[16]，并结合全局路径和障碍物信息，解算出最优跟随轨迹，并转化为小车驱动控制量，以控制小车行驶。搭建的系统如图4所示，实验场景如图5所示。

图4 车体系统实物

图5 实验场景

4.2 结果及分析

实验着重关注车辆在规避不同障碍的同时跟随全局路径的运动状态，设计了2组实验。第1组实验，在全局规划路径且车辆初始状态相同的情况下，记录车辆在存在障碍物和不存在障碍物的情况下跟随全局规划路径的运动状态。第2组实验，在障碍物位置相同但因大小、形状的不同，通过膨胀处理后膨胀区域半径不同的情况下，记录车辆跟随全局规划路径的状态。将3种不同障碍物预设写入算法系统中，观测能否解算出偏移量较小的避障跟随轨迹。由此，保持实验车体的初始状态一致，初始速度为2 m/s，初始位置与参考轨迹的偏差为1 m，最大加速度为2 m/s2，生成跟随待选轨迹的曲率，并限制在1 m−1，纠偏时间采样间隔为0.2 s，利用python工具包matplotlib绘制仿真效果图。

如图6—8所示，粗实线为全局参考路径，虚线为车辆最终的跟随轨迹，呈扇形的多条较细实线表示文中算法在规划采样点处求解得到的多条待选轨迹，五角星与虚线圆圈共同表示障碍物的位置与相应的膨胀区域，三角形表示车体在行驶过程中的规划采样点。在参考轨迹一致时，第1组实验中车体的跟随情况如图6～7所示。根据车辆跟随全局规划路径行驶过程中生成的行驶轨迹可知，车体在行驶过程中有效地绕过了障碍物，并有能力平滑跟随全局参考路径。在第2组实验中（图7～8），在相同参考路径和障碍物位置的情况下，将障碍物的膨胀半径分别设置为1 m和2 m，车辆的局部运动决策分别为从障碍物上方通过及从障碍物下方通过。通过分析可知，车辆在面对较大的障碍物时，继续选择上方通过会导致跟随轨迹与全局规划路径的偏差较大，从而求解出向下方通过的运动决策，满足了避障要求的同时，选择了偏移量更小的局部路径。由此可知，求解的最优跟随轨迹随着膨胀区域的变化而变化，车辆行驶能有效绕过障碍物，且平滑地跟随全局路径。

通过上述实验，验证了此避障算法在车辆相对于全局路径存在偏差时，能够有效求解平滑的跟随轨迹，并可根据障碍物的位置从待选轨迹中筛选出更合理的跟随轨迹，来决策控制车辆，能较好地满足路径规划中的避障要求。

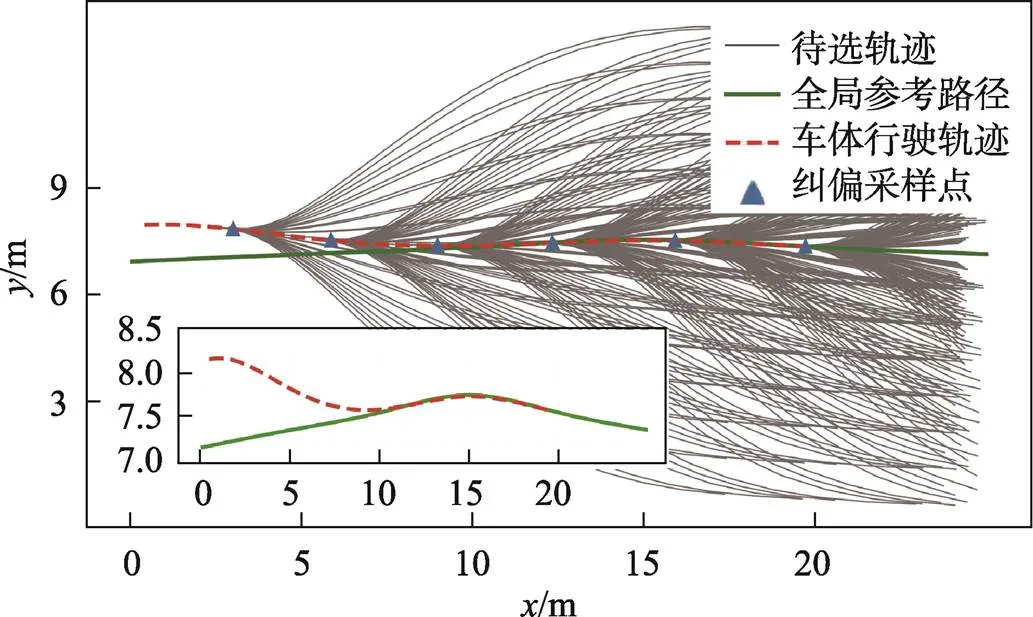
图6 无障碍物时车辆跟踪轨迹

图7 障碍物较小时车辆跟踪轨迹

图8 障碍物较大时车辆跟踪轨迹

5 结语

基于Frenet坐标框架数学模型，利用Frenet坐标系对车辆位姿和参考全局路径的高表达性，在Frenet框架下求解多条待选轨迹，且映射到笛卡尔坐标系中，通过障碍物膨胀来优化算法，筛选出具有避障能力的最优轨迹，进而控制车辆行驶，并进行了实测。

1）算法使得车辆平滑安全地跟随全局参考路径，并自主从起始点行驶到终止点。

2）算法求解的局部跟随轨迹平滑且兼顾避障，解决了车辆遇到障碍物行驶不连贯的问题。

3）通过实验验证，该算法能够使车辆在面对障碍物大小、形状不同的情况下做出相应的决策改变，使车辆面对不同环境具有较好的适应能力。

[1] 袁春, 龚城, 何成诚, 等. Frenet坐标系及凸近似避障原理的无人车局部路径规划[J]. 重庆理工大学学报(自然科学), 2022, 36(4): 59-67.

YUAN Chun, GONG Cheng, HE Cheng-cheng, et al. Local Path Planning for Unmanned Vehicles Based on Frenet Coordinate System and Convex Approximate Obstacle Avoidance Principle[J]. Journal of Chongqing University of Technology (Natural Science), 2022, 36(4): 59-67.

[2] 迟胜凯, 谢永芳, 陈晓方, 等. 基于障碍物代价势场的移动机器人避障算法[J]. 北京航空航天大学学报, 2022, 48(11): 2289-2303.

CHI Sheng-kai, XIE Yong-fang, CHEN Xiao-fang, et al. Obstacle Avoidance Algorithm of Mobile Robot Based on Obstacle Cost Potential Field[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(11): 2289-2303.

[3] 钱东海, 孙林林, 赵伟. 基于三次B样条曲线的叉车型AGV路径规划研究[J]. 计算机测量与控制, 2022, 30(4): 177-181.

QIAN Dong-hai, SUN Lin-lin, ZHAO Wei. Study on Forklift AGV Path Planning Based on Cubic B-Spline Curve[J]. Computer Measurement & Control, 2022, 30(4): 177-181.

[4] 赵明, 郑泽宇, 么庆丰, 等. 基于改进人工势场法的移动机器人路径规划方法[J]. 计算机应用研究, 2020, 37(S2): 66-68.

ZHAO Ming, ZHENG Ze-yu, YAO Qing-feng, et al. Path Planning Method of Mobile Robot Based on Improved Artificial Potential Field Method[J]. Application Research of Computers, 2020, 37(S2): 66-68.

[5] 朱佳莹, 高茂庭. 融合粒子群与改进蚁群算法的AUV路径规划算法[J]. 计算机工程与应用, 2021, 57(6): 267-273.

ZHU Jia-ying, GAO Mao-ting. AUV Path Planning Based on Particle Swarm Optimization and Improved Ant Colony Optimization[J]. Computer Engineering and Applications, 2021, 57(6): 267-273.

[6] 杨明亮, 李宁. 改进A*算法的移动机器人路径规划[J]. 机械科学与技术, 2022, 41(5): 795-800.

YANG Ming-liang, LI Ning. Study on Mobile Robot Path Planning Based on Improved A*Algorithm[J]. Mechanical Science and Technology for Aerospace Engineering, 2022, 41(5): 795-800.

[7] ATIYAH A N, ADZHAR N, JAINI N I. An Overview: On Path Planning Optimization Criteria and Mobile Robot Navigation[J]. Journal of Physics: Conference Series, 2021, 1988(1): 012036.

[8] SATHIYA V, CHINNADURAI M, RAMABALAN S. Mobile Robot Path Planning Using Fuzzy Enhanced Improved Multi-Objective Particle Swarm Optimization (FIMOPSO)[J]. Expert Systems With Applications, 2022, 198: 116875.

[9] 王沙晶, 陈建业. 基于Frenet坐标系的智能车运动规划研究[J]. 移动电源与车辆, 2019(1): 22-29.

WANG Sha-jing, CHEN Jian-ye. Motion Planning of Autonomous Vehicle Based on Frenet Coordinate System[J]. Movable Power Station & Vehicle, 2019(1): 22-29.

[10] 鲍久圣, 张牧野, 葛世荣, 等. 基于改进A*和人工势场算法的无轨胶轮车井下无人驾驶路径规划[J]. 煤炭学报, 2022, 47(3): 1347-1360.

BAO Jiu-sheng, ZHANG Mu-ye, GE Shi-rong, et al. Underground Driverless Path Planning of Trackless Rubber Tyred Vehicle Based on Improved A*and Artificial Potential Field Algorithm[J]. Journal of China Coal Society, 2022, 47(3): 1347-1360.

[11] 魏民祥, 滕德成, 吴树凡. 基于Frenet坐标系的自动驾驶轨迹规划与优化算法[J]. 控制与决策, 2021, 36(4): 815-824.

WEI Min-xiang, TENG De-cheng, WU Shu-fan. Trajectory Planning and Optimization Algorithm for Automated Driving Based on Frenet Coordinate System[J]. Control and Decision, 2021, 36(4): 815-824.

[12] ESHTEHARDIAN S A, KHODAYGAN S. A Continuous RRT*-Based Path Planning Method for Non- Holonomic Mobile Robots Using B-Spline Curves[J]. Journal of Ambient Intelligence and Humanized Computing, 2023, 14(7): 8693-8702.

[13] DURAKLı Z, NABIYEV V. A New Approach Based on Bezier Curves to Solve Path Planning Problems for Mobile Robots[J]. Journal of Computational Science, 2022, 58: 101540.

[14] XU Guo-qiang, JIANG Wei-lai, WANG Zhao-lei, et al. Autonomous Obstacle Avoidance and Target Tracking of UAV Based on Deep Reinforcement Learning[J]. Journal of Intelligent & Robotic Systems, 2022, 104(4): 60.

[15] 聂光明, 谢波, 田彦涛. 基于Frenet框架的协同自适应巡航控制算法设计[J]. 吉林大学学报(工学版), 2022, 52(7): 1687-1695.

NIE Guang-ming, XIE Bo, TIAN Yan-tao. Design of Cooperative Adaptive Cruise Control Algorithm Based on Frenet Framework[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(7): 1687-1695.

[16] 高扬, 徐永贵, 刘江. 基于GPS和视觉同步定位与建图的无人驾驶车辆定位方法研究[J]. 汽车技术, 2021(6): 19-24.

GAO Yang, XU Yong-gui, LIU Jiang. Research on Localization Method for Unmanned Vehicle Based on GPS and VSLAM[J]. Automobile Technology, 2021(6): 19-24.

Adaptive Obstacle Avoidance Algorithm Based on Frenet Coordinate Framework

KUANG Jun1a, YOU Jie1b, ZHONG Xiao-wan2, WAN Ren-zhuo1b, HAN Dong-gui1a, YAN Nu1a*

(1. a. School of Mechanical Engineering and Automation, b. School of Electronic and Electrical Engineering, Wuhan Textile University, Wuhan 430200, China; 2. School of Intelligent Manufacturing, Xiangyang Auto Vocational Technical College, Hubei Xiangyang 441021, China)

The work aims to address the difficulty of ensuring smooth following trajectories and obstacle avoidance at the same time when unmanned transport vehicles are travelling along a global path in the packaging workshop. The Frenet coordinate frame was constructed to describe the relative relationship between the vehicle pose and the global path. A quintic polynomial was adopted to generate multiple local paths to be selected.The obstacle profile of the packaging workshop was fuzzy processed by the obstacle potential field method, and the expansion interval was set. Combined with the collision values calculated for the sampling points of the path to be selected in the obstacle expansion interval, and the deviation values of the sampling points from the globally planned paths, the obstacle avoidance quality of the local paths was comprehensively evaluated to filter out the optimal obstacle avoidance path. According to the size of obstacles, the algorithm could dynamically calculate the local obstacle avoidance path with small offset from the global path and coherent motion. The proposed algorithm makes the vehicle complete the transport task with better effect and higher efficiency.

local path planning; obstacle avoidance algorithm; optimal path; Frenet coordinate system; adaptive

TP242

A

1001-3563(2023)19-0165-06

10.19554/j.cnki.1001-3563.2023.19.021

2022-11-28

国家自然科学基金（51775388）

责任编辑：彭颋