考虑多基地拖轮使用平衡性的重调度优化

钟铭，张梦迪

自动化与智能化技术

考虑多基地拖轮使用平衡性的重调度优化

钟铭，张梦迪

（大连海事大学 交通运输工程学院，辽宁 大连 116026）

解决多停泊基地背景下拖轮与船舶之间供需不匹配、需求响应时效要求越来越高以及各基地拖轮使用不平衡等问题。本文考虑多拖轮基地的影响，在对拖轮线路调度的基础上进行区域调度，采用对拖轮进行跨基地重调度的方法，以总调度成本最小为目标建立拖轮重调度模型。将天津港数据搜集分析作为本文案例对模型进行验证分析，结果显示，采用区域调度后成本低于单纯的线路调度，且拖轮工作时间基尼系数值为0.2～0.3，处于比较公平的状态。此模型有效地降低了拖轮调度成本和在港船舶等待时间，平衡了拖轮使用时间。

多拖轮基地；数据分析；线路调度；区域调度；重调度

如今拖轮基地通常采用离散式布局，将不同马力的拖轮配置在指定的基地。但是在某基地服务的船舶进港时间较密集时，船舶等待时间会增加，若其他基地拖轮空闲，则会存在拖轮使用不均衡的问题，仅靠基地内的线路调度并不能很好地解决拖轮与船舶的供需关系。调度除线路调度外还有区域调度的方式，他们的区别在于线路调度是将各基地视作单独个体，在其内部进行调度。区域调度则将多个基地视作一个整体，可进行基地间的联合调度，这种调度方式可以平衡拖轮利用率，提高服务效率。因此，本研究通过基地间区域调度的方式，对快速响应船舶的需求，提高拖轮工作的灵活性，降低拖轮工作成本具有重要意义。

当前，针对拖轮的研究主要是拖轮资源整体的配置和调度问题。Wang等[1]、Abou等[2]研究了拖轮与船舶的匹配关系及船舶服务顺序。Chen等[3]对拖轮活动特性进行了分析，其研究对拖轮配置、调度等有一定的指导意义。郑红星等[4]、Yu等[5]设计了拖轮配置方案仿真模型。刘春建[6]除了拖轮配置方案还设计了基地选址模型。但如今更多的则是针对拖轮调度的研究。Wu等[7]以作业总成本最小化为目标，利用了分支定界法来解决拖轮调度问题。Kang等[8]在拖轮调度的研究中对船舶等待时间进行了限制。Jia等[9]考虑了泊位计划和可用拖轮的数量限制、船舶停泊和离港延误时间，以及部分船舶无法被服务的情况。Zhang等[10]不仅考虑了船舶等待时间，还考虑了航道占用时间。但大部分的拖轮调度研究是针对一个拖轮基地的，而越来越多的港口已经采用了多基地的经营模式，Wei等[11]对多基地布局方式的经济性进行了分析与肯定。徐奇等[12]最早提出了多基地拖轮调度的意义，以距离最小化为目标研究了2个停泊基地的拖轮调度问题。王巍等[13]设计的模型目标中考虑了最大完成时间和燃油成本。李伯棠等[14]在多基地拖轮调度中考虑了拖轮完成一项任务后可停靠任意停泊基地的情况。大部分的拖轮调度是针对单基地的研究，多基地的拖轮调度研究较少且仍存在一些研究缺陷，其他领域多站点调度的研究可以给予一些借鉴。如王妍妍等[15]在应急物资分配中提出了区域自救与跨区域协同救援的方式，兼顾了效率与公平。Lei等[16]对需求进行了预测，在需求产生之前对车辆进行区域调度。Boujemaa等[17]用两阶段随机规划解决了救护车区域调度问题。

本文根据现有文献的不足，对多基地拖轮调度问题进行了研究。主要贡献如下：针对多拖轮基地的特点考虑拖轮使用不平衡的因素，模型中引入基尼系数的限制；在燃油成本中考虑不同类型拖轮工作成本的不同，并以燃油成本最小化为规划目标；考虑拖轮完成上一任务后可从上一任务完成地点直接到下一任务地点的情况；在线路调度的基础上设计区域调度的方式，并收集天津港真实数据对模型进行验证。

1 问题描述

本文对船舶位置、进/离港需求、船长、船舶类型等进行分析，限制船舶最长等待时间。将任务分配给对应基地的拖轮，若对应基地拖轮在时间限制内不能满足船舶的需求，则进行重调度，将调度任务分配给其他基地拖轮。综上，本文研究的调度问题属于在拖轮线路调度的基础上进行空间重调度，其目标为总调度成本最小。

在港口实际生产作业过程中，按照船舶的船长将其划分为不同的类型。不同类型的船舶所需的拖轮马力数和艘数有着不同的要求，表1表示了拖轮实际作业时与船舶的配比关系。船舶按照船长分为5类，分别代表100 m以下、[100，200)m、[200，250)m、[250，300)m和300 m及以上[18]。拖轮按照功率分为8种类型，所表示的功率分别为1 911、2 352、2 499、2 940、3 675、3 822、4 410和4 777.5 kW。

表1 拖轮与船舶的配比关系

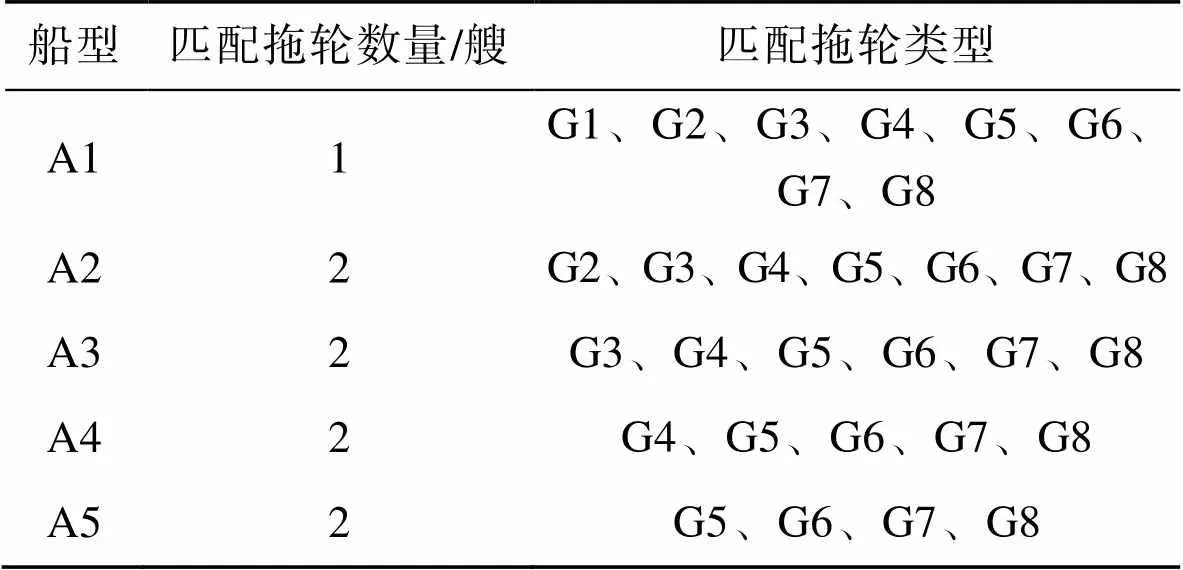
Tab.1 Ratio relationship between tug and ship

2 模型建立

2.1 建立步骤

模型建立步骤如下：

1）获取到港船舶的基本信息并对数据进行处理，确定被服务船舶到港的时间分布和最大等待时间。

2）根据船型划分被服务船舶吨位等级，并确定所需的拖轮数量及马力需求。

3）建立整数规划模型，确定进行重调度的拖轮及其移动方式。

2.2 模型假设

1）考虑靠泊和离泊2个作业过程。

2）拖轮调度涉及的位置包括船舶作业泊位、锚地及拖轮停泊基地。

3）拖轮移动的原则为就近原则，避免对同一拖轮多次或往返移动。

4）拖轮的速度是相同的，与拖轮服务的船舶吨位等级无关。

2.3 参数和变量设定

参数和变量设定如表2—4所示.

表2 集合定义

Tab.2 Definition of sets

表3 参数定义

Tab.3 Definition of parameters

表4 决策变量定义

Tab.4 Definition of decision variables

2.4 调度模型：

目标函数：

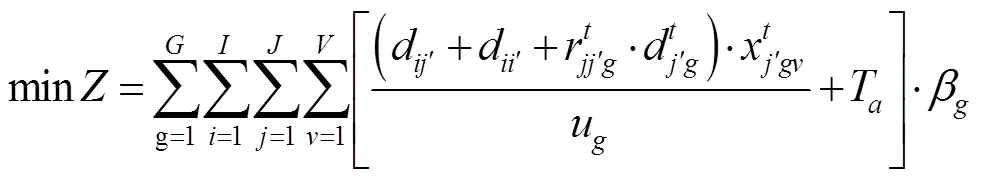
约束条件：

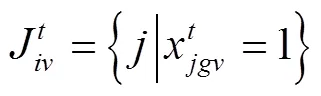
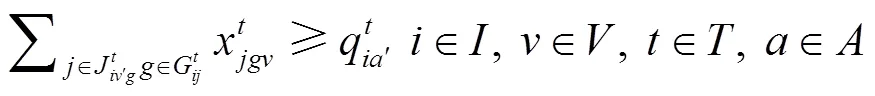
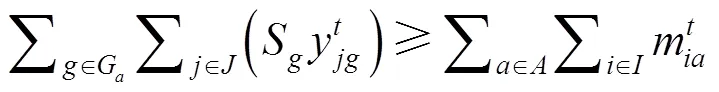
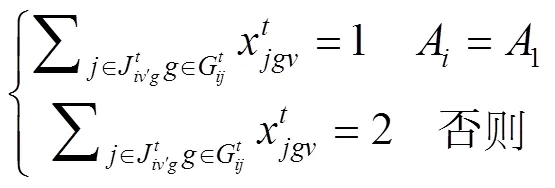
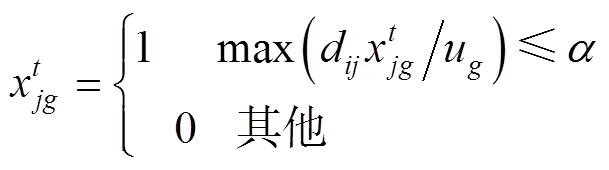
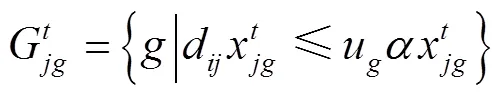
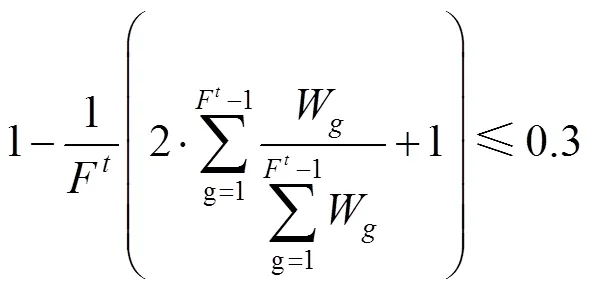
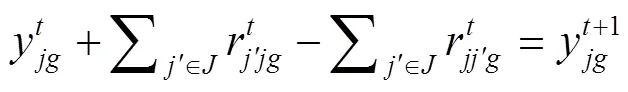
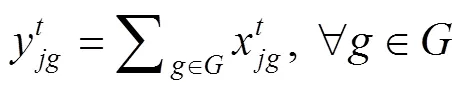
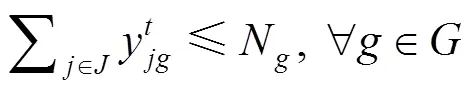
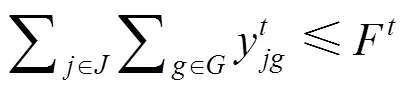
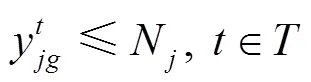
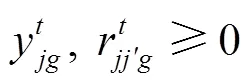
式（1）为目标函数，表示拖轮的总调度成本最小。式（2）～（7）表示在时间能够有足够数量、足够马力的拖轮能够到达作业位置为船舶服务。式（8）引入基尼系数的概念保证拖轮工作的平衡性；式（9）为重调度数量约束，表示经历拖轮的调度后基地的拖轮数量变化，+1时期的拖轮数等于时期；式（10）表示时期在拖轮基地配置的型拖轮艘数；式（11）表示所有基地分配的拖轮数不能超过该类型拖轮的总数；式（12）表示每个时间段分配给各基地的拖轮数量应小于该时间段可用的拖轮数量；式（13）为各基地的容量约束。

3 模型求解

本文研究的多拖轮基地区域调度问题，属于NP-Hard问题，找到精确解会十分困难，而近似优化算法对此问题的求解具有一定的优势。遗传算法的搜索方式灵活，具有结果稳定，求解效率高的优点。综合考虑遗传算法的特点，本文采用遗传算法对模型求解。首先采用双染色体的编码方式对拖轮基地及船舶进出港任务编码，将船舶进出港任务编码分配给拖轮，根据分配的进出港任务编码次序对拖轮调度。解码方法是根据进出港任务编码与基地编码相对应再进行拖轮分配。以拖轮调度总成本最小为适应度函数。通过限制种群中个体的生成方式来满足模型约束，根据个体的适应度大小，用轮盘赌的方法挑选个体，用单点交叉和小概率变异进行遗传操作对模型进行求解。

求解流程是依据先到先服务和大船优先原则选定被服务的船舶，并根据其靠泊区域确定拖轮基地；分析基地能够在时间限制内能为船舶服务的拖轮，根据船舶对拖轮的马力要求确定拖轮的类型和数量，按照燃油消耗成本最小确定具体拖轮，完成一艘在港船舶的服务。

针对被服务船舶：若其所需拖轮数量或等待时间限制不能满足，则需针对拖轮继续决策下一拖轮基地；若要求已满足，则继续依据服务时限和大船优先原则选定下一艘被服务的船舶+1和拖轮，直到将所有被服务船舶均被服务，流程如图1所示。

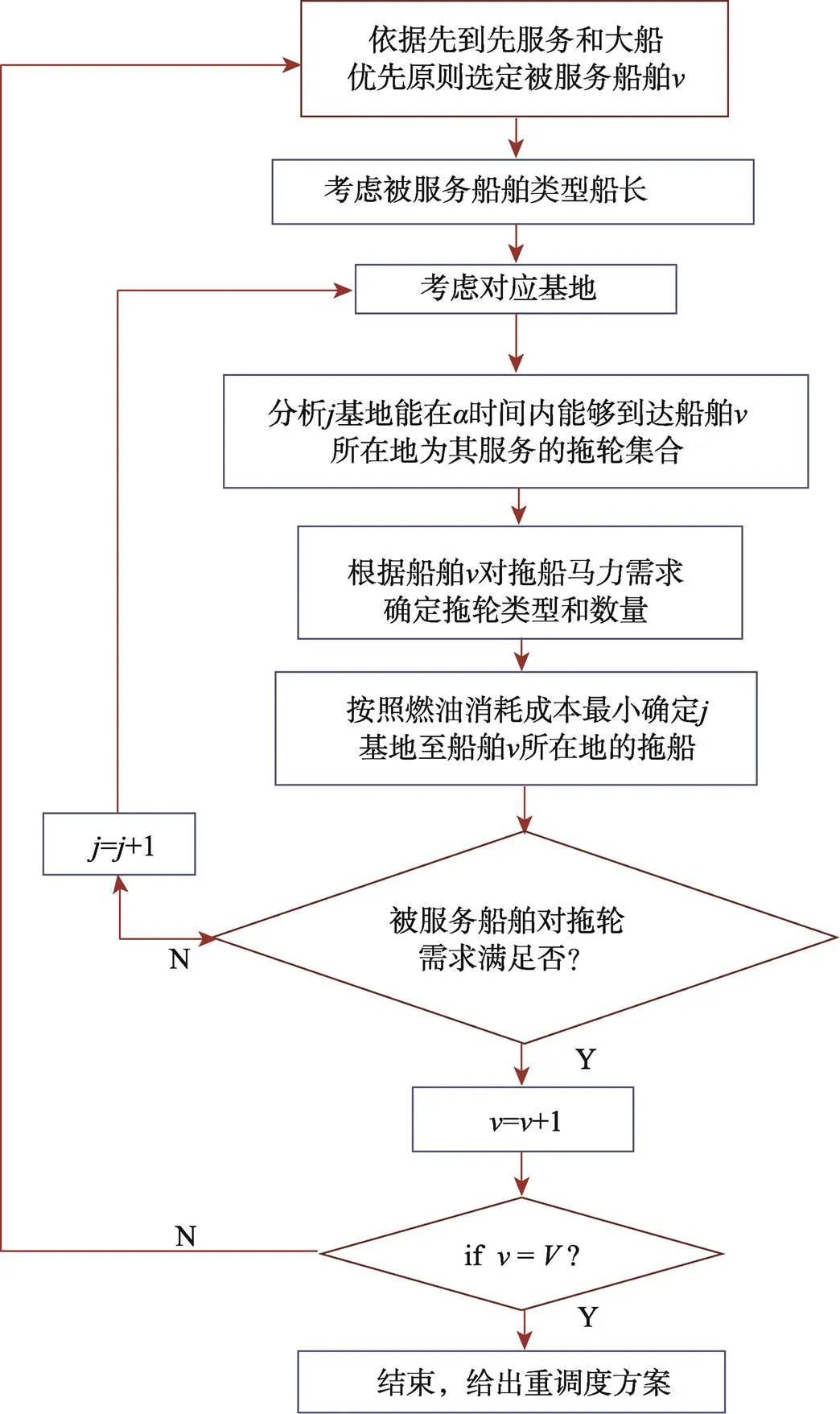
图1 模型求解流程

4 结果与分析

4.1 算例信息

为了便于模型求解，将天津港拖轮分布情况，随机分配在4个拖轮停泊基地，作为拖轮的初始位置，并给各拖轮分配虚拟编号。具体如表5所示。

基地的虚拟编号、容量限制编号以及具体配置情况如表6所示。

表5 天津港拖轮信息

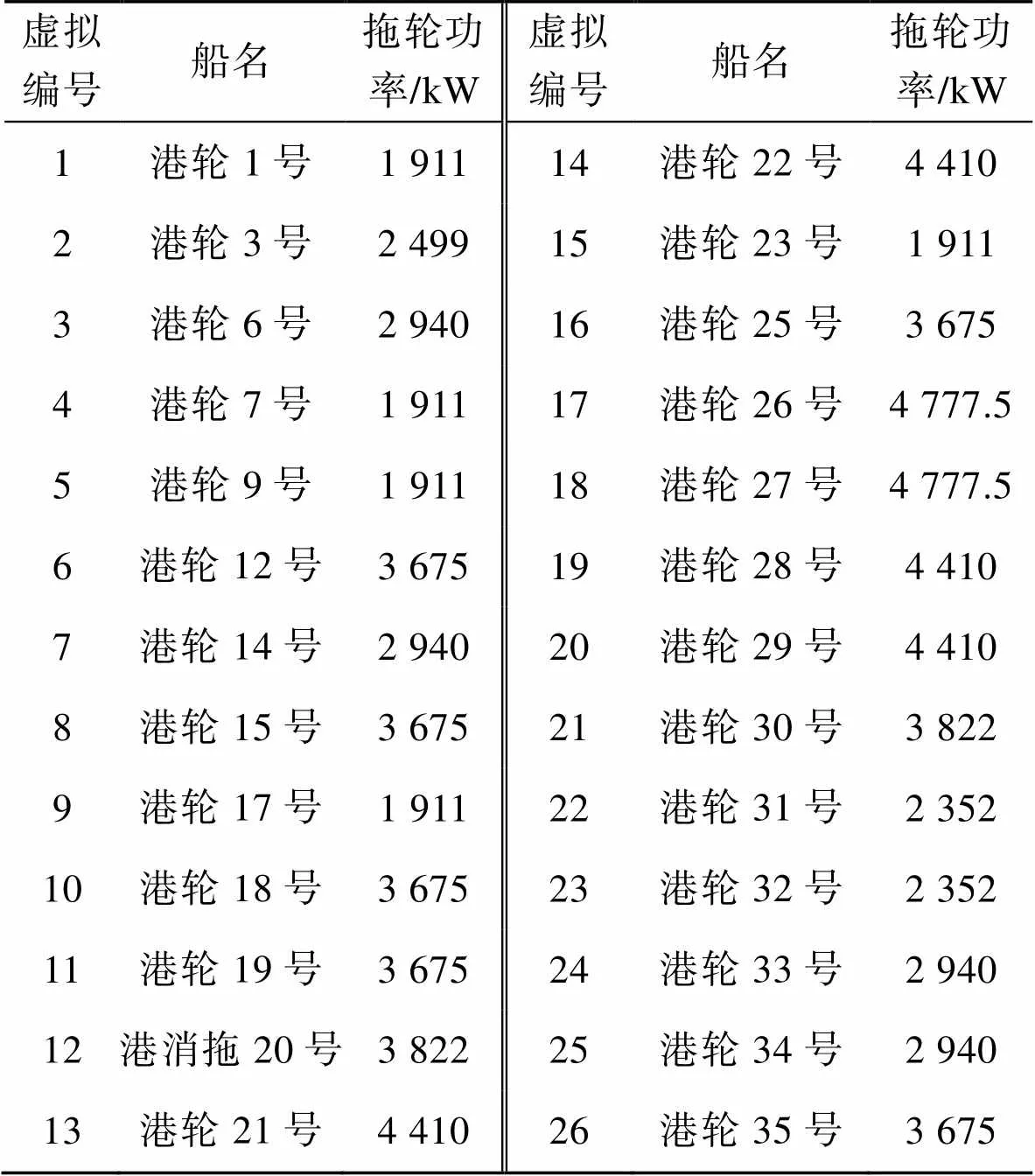
Tab.5 Tug information in Tianjin Port

表6 天津港拖轮基地信息

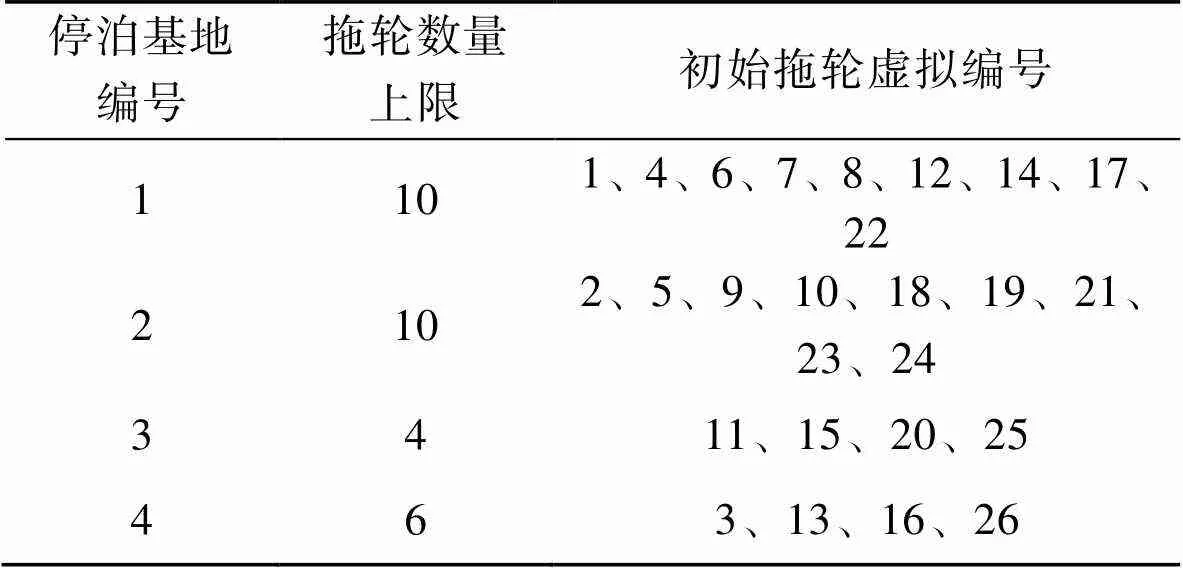
Tab.6 Tug base information in Tianjin Port

提取2021年8月1日0:00至8月2日0:00天津港船舶进出港数据，将处理后的数据作为算例进行研究。由2021年8月天津港船舶在港时间及在泊时间得出船舶平均等待时间为8.64 h，因此取=8.64。图2为本文研究中涉及到的锚地和拖轮停泊基地位置示意。

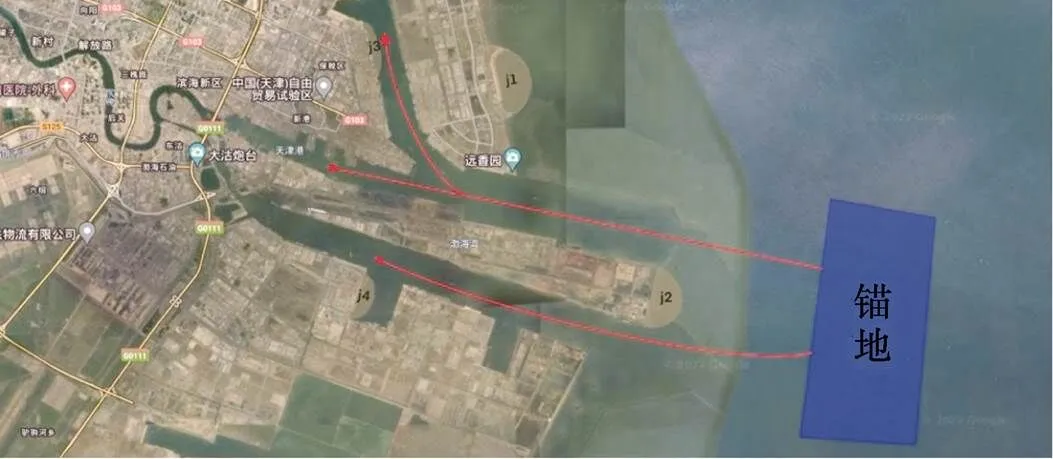
图2 拖轮基地、锚地位置示意图

利用海图数据信息确定锚地、泊位及拖轮停泊基地的位置数据，取锚地边界、各泊位及拖轮基地中心。为了便于问题的求解，将实际问题合理简化，按照在港船舶实际靠泊的地理位置划分区域，为船舶分配虚拟靠泊位置B1～B9，图3为泊位区位置示意。

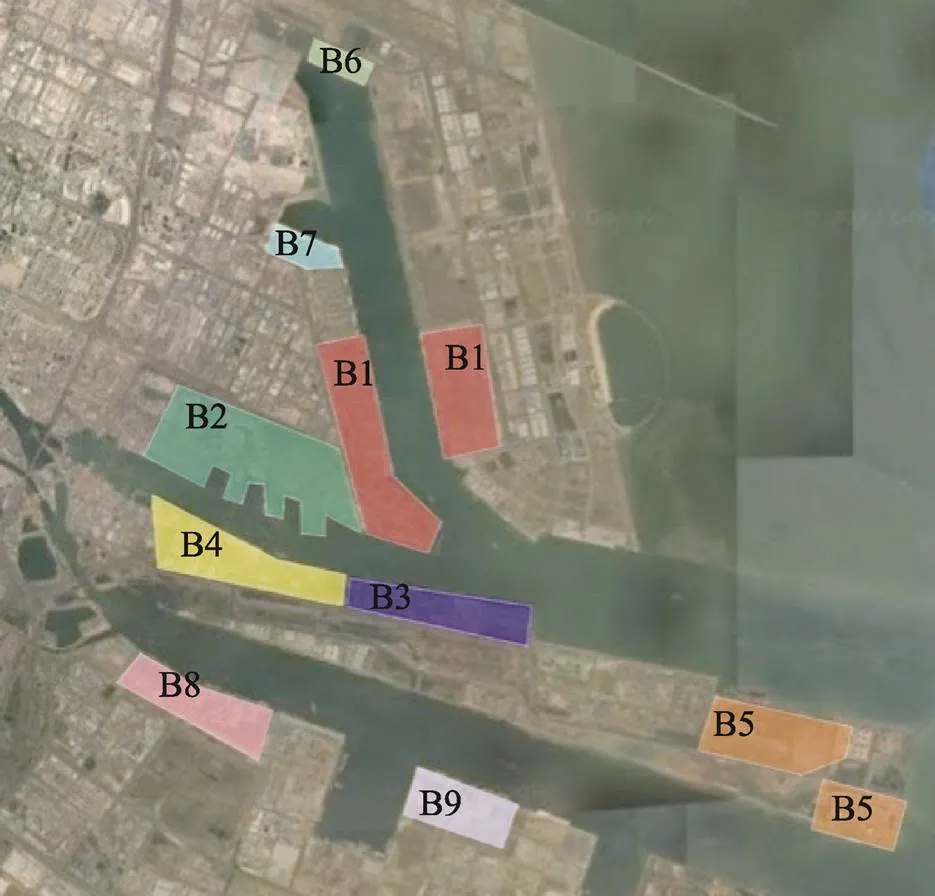
图3 泊位区位置

本文采用计算直角距离的方式来近似替代，取一分纬线距离等于1.86 km，一分经线距离等于1.442 km进行计算。

4.2 实验结果

将设计的模型用Matlab R20212b求解，得到方案：港轮17号在8:00时由基地2调度到基地3，港消拖20号在10:36时由基地1调度到基地2，港轮34号在15:12时由基地3调度到基地1，港轮6号在16:48时由基地4调度到基地2，重调度开始情况如图4所示。各拖轮工作时长如表7所示。

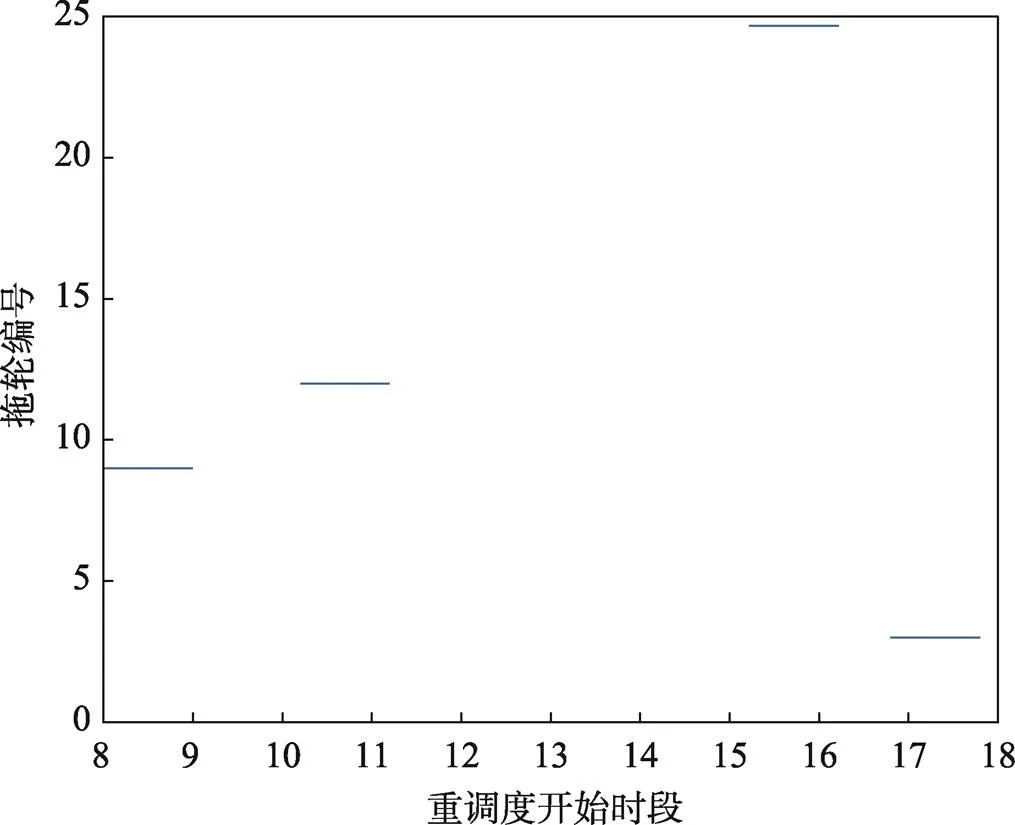
图4 重调度开始情况示意图

表7 拖轮工作时长

Tab.7 Tug working hours

验证计算其基尼系数等于0.281 962 33，其区间为0.2～0.3，从其结果上来看各拖轮工作时长比较公平。由实验结果也可得知，采用动态配置优化后的成本低于不采用动态配置优化的成本，成本结果如图5、图6所示。模型中限制船舶等待时间阈值也使得在港船舶等待平均时间变短。

分析得到该结果的主要原因为港口拖轮资源有限，当在港船舶达到一定数量后，拖轮使用频率增加。若本基地中的拖轮无空闲，在港船舶须等待其完成上一作业任务后再进行作业，此时使用其他停泊在基地中有空闲的拖轮来完成作业，则可减少船舶在港等待时间，且从空闲停泊基地到达作业位置的距离成本会低于本基地拖轮在上一工作地点到达作业位置的距离成本。因此在拖轮调度过程中采用动态配置的方法可以有效减少拖轮作业成本，减少船舶在港等待时间，提高服务效率。

图5 重调度前最优解目标值变化

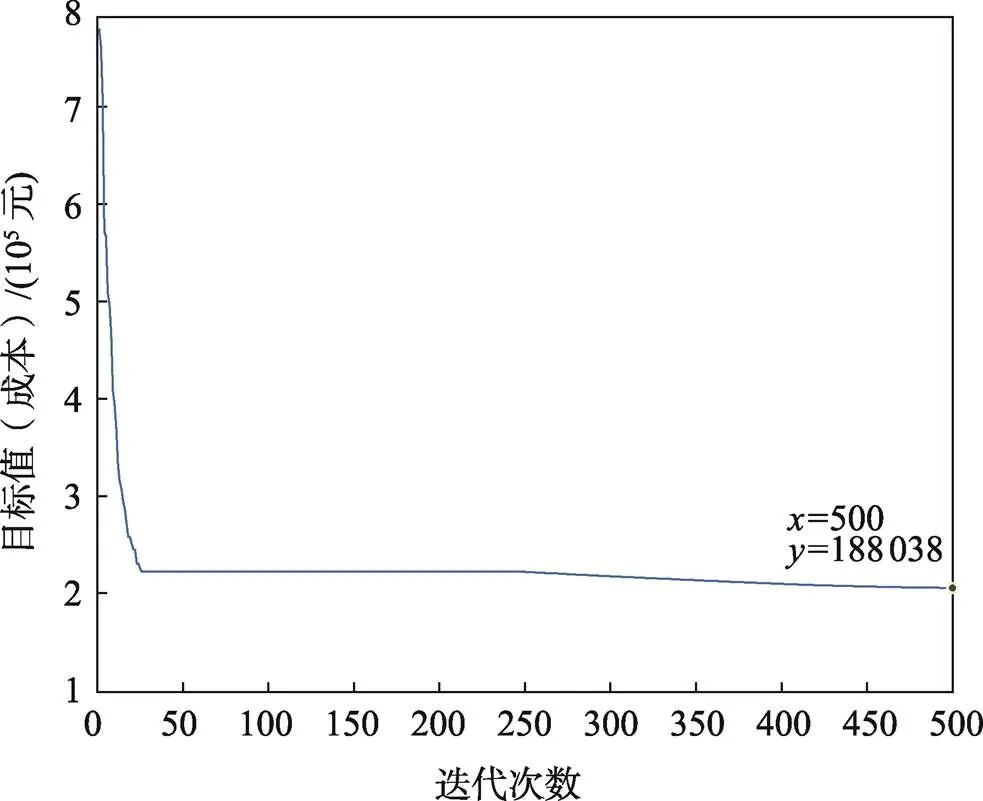
图6 重调度后最优解目标值变化

5 结语

本文构建了拖轮重调度模型，用遗传算法进行求解，选取了天津港水域信息对模型进行实例验证，结果显示此模型有效降低了拖轮调度成本及在港船舶等待时间。主要贡献体现在考虑了各基地拖轮使用不平衡的问题，在拖轮线路调度的基础上进行了区域调度，通过这种方式减少了船舶的等待时间，对拖轮使用不平衡的问题起到了一定的改善作用；从人性化角度考虑也能够平衡引航员之间的工作时长，缩小收入差距。

[1] WANG Su, ZHU Min, KAKU I, et al. An Improved Discrete PSO for Tugboat Assignment Problem under a Hybrid Scheduling Rule in Container Terminal[J]. Mathematical Problems in Engineering, 2014, 22: 1-10.

[2] ABOU K O, DIABAT A, OZBAY K. Vessel Scheduling under Different Tugboat Allocation Policies[J]. Computers & Industrial Engineering, 2023: 108902.

[3] CHEN Shu-kai, WANG Feng, WEI Xiao-yang, et al. Analysis of Tugboat Activities Using AIS Data for the Tianjin Port[J]. Transportation Research Record Journal of the Transportation Research Board, 2020, 2674(5): 498-509.

[4] 郑红星, 徐海栋, 曹红雷. 复式航道港口拖轮配置仿真优化[J]. 重庆交通大学学报(自然科学版), 2017, 36(8): 102-109.

ZHENG Hong-xing, XU Hai-dong, CAO Hong-lei. Simulation Optimization of Compound Channel Port Tugboat Configuration[J]. Journal of Chongqing Jiaotong University (Natural Sciences), 2017, 36(8): 102-109.

[5] YU Wen-hui. Heuristic Algorithm for Simulation and Optimization System of Port Tugboats Allocation[C]// International Conference on Internet Computing & Information Services, IEEE, 2011.

[6] 刘春建. 大连港拖轮停泊基地选址及配置优化研究[D]. 大连: 大连海事大学, 2018.

LIU Chun-jian. Study on the Location and Allocation Optimization of Dalian Port Tugboat Berth Base[D]. Dalian: Dalian Maritime University, 2018.

[7] WU Ling-xiao, JIA Shuai, WANG Shuai-an. Pilotage Planning in Seaports[J]. European Journal of Operational Research, 2020, 287(1) : 90-105.

[8] KANG Liu-jiang, MENG Qiang, TAN K C. Tugboat Scheduling under Ship Arrival and Tugging Process Time Uncertainty[J]. Transportation Research Part E Logistics and Transportation Review, 2020, 144(3): 102125.

[9] JIA Shuai, LI Shu-qin, LIN Xu-dong, et al. Scheduling Tugboats in a Seaport[J]. Transportation science, 2021(6): 55.

[10] ZHANG Xin-yu, LI Rui-jie, CHEN Xiang, et al. Multi-Object-Based Vessel Traffic Scheduling Optimisation in a Compound Waterway of a Large Harbour[J]. Journal of Navigation, 2018, 72(3): 1-19.

[11] WEI Xiao-yang, MENG Qiang, LIM A, et al. Dynamic Tugboat Scheduling for Container Ports[J]. Maritime Policy & Management, 2021, 50(4): 1-23.

[12] 徐奇. 港口拖轮调度优化及其仿真研究[D]. 大连: 大连海事大学, 2012.

XU Qi. Optimization of Port Tugboat Scheduling and Its Simulation Research[D]. Dalian: Dalian Maritime University, 2012.

[13] 王巍, 赵宏, 李强. 面向多停泊基地的港口拖轮调度优化研究[J]. 计算机工程与应用, 2013, 49(13): 8-12.

WANG Wei, ZHAO Hong, LI Qiang. Multi-Objectives Optimization for Port Tugboat Scheduling Considering Multi-Anchorage Bases[J]. Computer Engineering and Applications, 2013, 49(13): 8-12.

[14] 李伯棠, 王智利, 周海英, 等. 港口拖轮调度模糊规划优化模型及算法[J]. 计算机集成制造系统, 2021, 27(5): 1518-1530.

LI Bo-tang, WANG Zhi-li, ZHOU Hai-ying, et al. Fuzzy Programming Model and Algorithm of Port Tugboat Scheduling[J]. Computer Integrated Manufacturing Systems, 2021, 27(5): 1518-1530.

[15] 王妍妍. 地震灾害应急物资多周期分配优化模型研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.

WANG Yan-yan. Study on Multi-Period Allocation Optimization Model of Emergency Materials for Earthquake Disaster[D]. Harbin: Harbin Institute of Technology, 2019.

[16] LEI Zeng-xiang, QIAN Xin-wu, UKKUSURI S. Efficient Proactive Vehicle Relocation for On-Demand Mobility Service with Recurrent Neural Networks[J]. Transportation Research Part C Emerging Technologies, 2020, 117(10): 1-17

[17] BOUJEMAA R, JEBALI A, SONDES H, et al. Multi-Period Stochastic Programming Models for Two- Tiered Emergency Medical Service System[J]. Computers & Operations Research, 2020, 123: 104974.

[18] 徐奇, 邵乾虔, 靳志宏. 基于混合流水作业组织的港口拖轮调度优化[J]. 系统工程理论与实践, 2014, 34(2): 485-493.

XU Qi, SHAO Qian-qian, JIN Zhi-hong. Optimization on Tugboat Operation Scheduling Based Upon the Hybrid Flow Shop Arrangement[J]. Systems Engineering-Theory & Practice, 2014, 34(2): 485-493.

Rescheduling Optimization Considering the Use Balance of Multi-base Tugs

ZHONG Ming, ZHANG Meng-di

(College of Transportation Engineering, Dalian Maritime University, Liaoning Dalian 116026, China)

The work aims to solve the problems of mismatch between supply and demand of tugs and ships, increasing demand response timeliness requirements, and unbalanced use of tugs in various bases. Considering the impact of multiple tug bases, regional scheduling was carried out on the basis of tug line scheduling, and a tug rescheduling model was established with the goal of minimizing the total scheduling cost by adopting the method of cross-base rescheduling. With the data collected and analyzed from Tianjin Port as the case, the model was verified and the results showed that the cost after regional scheduling was lower than that of simple line scheduling, and the Gini coefficient of tug working time was 0.2 ～ 0.3, which was in a relatively fair state. The model effectively reduces the cost of tug scheduling and the waiting time of ships in port, and balances the use time of tugs.

multi tug base; data analysis; line scheduling; regional scheduling; rescheduling

TP391

A

1001-3563(2023)19-0158-07

10.19554/j.cnki.1001-3563.2023.19.020

2023-01-14

国家社会科学基金项目（22BGJ034）

责任编辑：曾钰婵