浅谈整体观下图形变化的层级探究

崔丽楠

摘要：初中阶段，图形的变化主要为折叠（轴对称）、旋转、平移这三类基本的图形运动。“图形的变化”强调从运动变化的观点来研究图形，理解图形在轴对称、旋转和平移时的变化规律和变化中的不变量。图形折叠的相关知识、解题方法等在不同年级和章节比较零散，不够系统全面。大单元教学的核心目标就是将零散的知识进行整合，将知识进行关联。[1]

关键词：整体结构 图形的变化 折叠

在目前的学校教学中，发展学生的核心素养已成为必然趋势。 核心素养具有整体性、一致性和阶段性，在不同阶段具有不同表现。《新版课程标准解析与教学指导（2022年版）》更加强调了知识的整体性和连贯性，到了初中阶段，学生对图形的理解上升到对图形性质、关系、变化规律的理解，因此要培养学生初步的抽象能力、理性思维、几何直观和空间想象力，能在实际情境中，识别出生活中的轴对称、平移和旋转的现象，并能直观感受平移、旋转和轴对称的特征。[2]图形的折叠（轴对称）是几何图形三种图形变换中的一种。北师大版教材呈现的知识结构与各时段的课标要求不同。而九年级时，图形折叠问题综合性比较强，解题思路比较广，解题方法灵活。所以，对图形的变化在不同学段进行不同的渗透是非常有意义的。在学习了角平分线和平行线之后，笔者以折叠中探究平行线性质与判定为例，浅谈大单元教学引导下，在七年级如何渗透图形的变化。

一、教学过程

（一）一次操作，初步感知

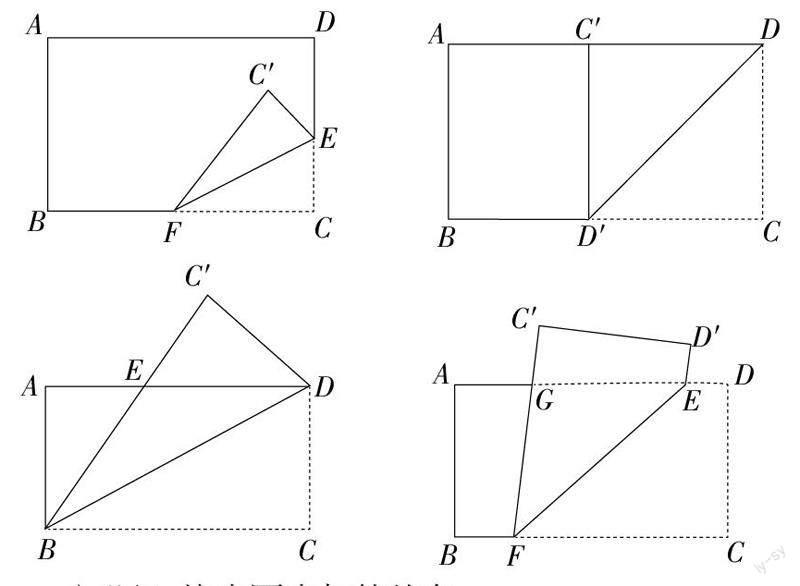
学生动手操作，折叠一张矩形纸片。 观察折叠后相等的角。展示学生的折叠作品如下：

问题1：找出图中相等的角。

问题2：图2中，∠AC′D′的度数是多少？

问题3：图3中，三角形EBD的形状？

问题4：图4中，图中有几组平行线？若∠EFC=40°，则∠GED′的度数？

功能分析：折纸活动对于七年级的学生来说是件有意义的事情，能激发学生的学习积极性。在操作过程中，通过大家不同的折纸方式，首先可以通过操作感受数学中的分类思想。其次，通过观察，直观感受折叠的轴对称作用，从而找到相等的角，利用问题串，将探究的问题一步步加深。问题1通过找相等的角感受折痕的角平分线的作用。问题2感受折叠前后的全等，边相等、角相等。问题3将角平分线与平行线结合，利用平行线的性质，得到∠EBD=∠EDB。

问题4发现存在两组平行线，两组平行线的结合，两组角平分线的结合进行求解。本次操作活动，既发展了学生的动手操作能力，又提升了学生的归纳总结能力。

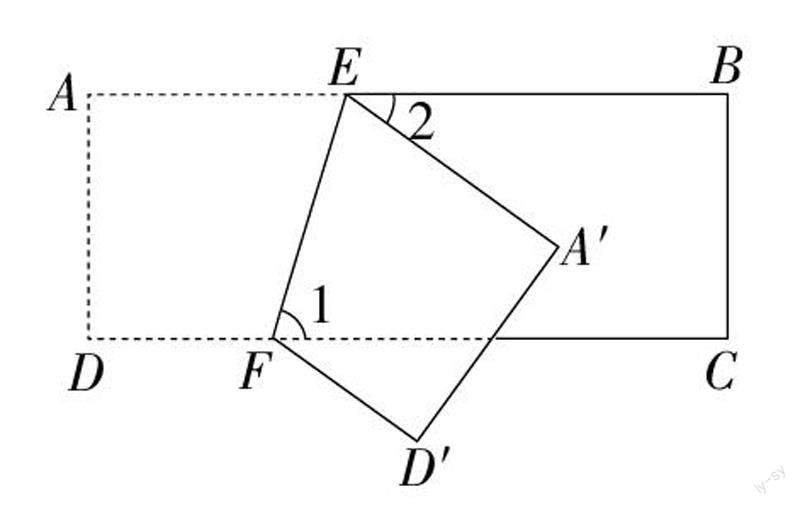
例1：如图，四边形ABCD为一矩形纸带，点E、F分别在边AB、CD上，将纸带沿EF折叠，点A、D的对应点分别为A'、D'，若∠2=35°，则∠1的度数为（）?

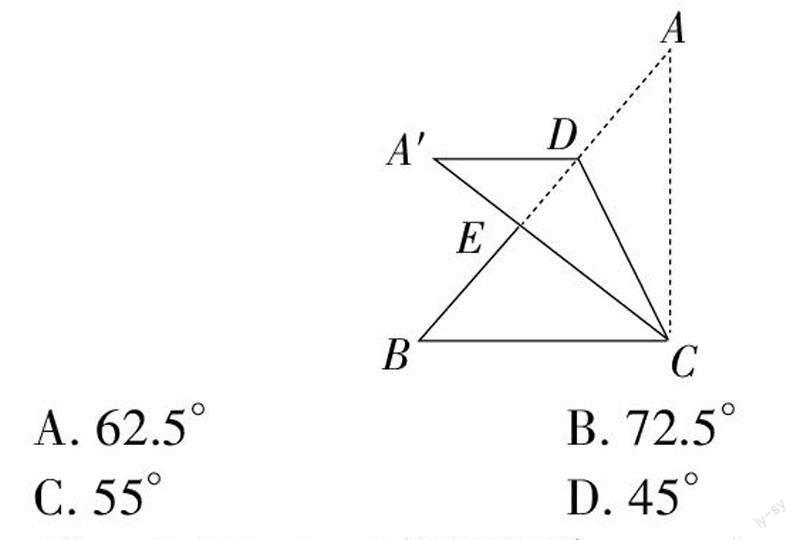
例2：如图，在三角形纸片ABC中，∠ACB=90°，∠A=40°，点D在AB边上（不与A、B重合），连接CD，将△ACD沿CD所在直线折叠得到△A′CD，A′C交AB于点E.如图，若A′D∥BC，则∠ACD的度数为     ；

设计意图：小试牛刀，例1将折叠与矩形结合，既加深折痕是角平分线的作用，又结合平行线的性质来求解。例2通过折叠三角形，巩固折叠前后对应角相等，折痕是角平分线的作用。对学生通过操作观察得到的结论转化为实践探究，发展理性思维能力。

（二）二次操作，总结归纳

例3：如图，长方形纸片ABCD，点E，F分别在边AB，CD 上，连接EF，将∠BEF对折，点B落在直线EF上的B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN，则∠MEN的度数为_________。

功能分析：在活动一中图1的基础之上继续进行操作，通过二次折叠，继续感知折痕是角平分线的作用。 通过实际操作，学生可观察出七年级上册学习角平分线时涉及到的双角平分线模型，此过程学生由实践操作再次进行提炼、归纳总结。

例4：如图，长方形纸片ABCD，将∠ADC和∠ABC分别沿着DD′、BB′对折，使得点A落在边CD上，点C落在边AB上，请问两条折痕DD′、BB′的位置关系如何？为什么？

功能分析：在活動一的图2基础之上继续进行操作，结合七年级所学的平行线知识，将角平分线和平行线相结合。教师在引导学生解题的过程中，领着学生进行分析结论，分析条件。学生经历观察猜想，验证推理的过程。

变式练习：（2023春·太原期中变式）综合与实践

问题情境：

数学课上，同学们以“长方形纸带的折叠”为主题开展数学活动，已知长方形纸带的边AD∥BC，将纸片沿折痕EF折叠，点A，B分别为点A'，B'，线段B′F与DE交于点G。（说明：折叠后纸带的边A′E∥B′F始终成立）

操作探究：

（1）如图1，若B′F⊥AD，则∠EFG的度数为_________°；

（2）如图2，改变折痕EF的位置，其余条件不变，小彬发现图中∠1=∠2始终成立，请说明理由；

（3）改变折痕EF的位置，使点 B'恰好落在线段AD上，然后继续沿折痕MN折叠纸带，点M，N分别在线段FC和B′D上.如图3，点C，D的对应点分别为点C′，D′，点C′，D′均在AD上方，若∠BFE=α，∠CMN=β，当FB′∥MC′时，直接写出α与β之间的数量关系。

例5：如图，把长方形ABCD的两角折叠，折痕分别为EF、HG，点B、D折叠后的对应点分别是B'、D'，并且使HD'与B'F在同一直线上，已知长方形的两组对边分别平行，试找出图中相互平行的直线。

功能分析：难度升级，问题具有开放性。学生自己找出平行线段，首先需要经历直观观察，猜想再进行证明。 此题综合性较强，但还是需要抓住其本质，在折叠过程中，哪些量是不变量，比如∠EB'F=90°，∠HD'G=90°，从而得到EB'∥D'G。 另一方面，折叠过程中，抓住折痕相当于角平分线这一特征，如∠GHD'=1/2∠DHF，∠EFB'=1/2∠BFH。又∠DHF=∠BFH，从而得到EF∥GH。 本节课的探究方式对于后续图形的变化的学习具有方法上的点拨。

变式练习：如图所示，一张长方形纸片ABCD（∠A=∠B=∠C=90°），先将纸片沿EF折叠，再将折叠后的纸片沿GH折叠，使得GD′与A′B′重合，展开纸片后若∠BFE=62°，则∠DGH=_________°。

二、教学思考

（一）整体结构性有助于眼中有木，心中有林

图形的运动，平移、旋转、轴对称对于九年级的学生来说，是至关重要的，并且难度也比较大。 将本节课内容放到整个几何知识板块中，只是一小部分而已。当然，在学习了三角形之后，将折叠与三角形相结合。 学习轴对称之后，折痕还具有中垂线的作用，但是通过本节课的学习，学生在后续的探究中，就会学会从什么角度入手来进行探究。 在初一阶段，将折叠的求角度问题渗透，在八年级学习了勾股定理，将折叠与求边长相结合。 学习了平面直角坐标系，再将图形折叠放到平面直角坐标系中进行研究。九年级学生在进行探究与思考时，对于此类型题目就会游刃有余。 但我们在本阶段教学时一直在强调关键词“角平分线”，并且一直在关注不变量，抓住本质所在。

（二）即时归纳提炼有助于整体知识建构

我们一直想让学生积极参与课堂，努力做到不仅课堂高效，而且学生乐学。本节课重在学生动手操作，独立思考，教师引导。设计体现了操作的本质和特征。重点研究操作前后对应线段、对应角的变与不变。强调由操作得到的图形之间特殊的位置关系和数量关系。此外，教学设计不止于操作，还把操作活动上升到思维层面，把实际问题转化为数学问题。将本质的、共同的、核心的要素进行即时性的归纳总结，培养学生进行直观猜测、数学抽象、逻辑思维等。这种研究图形变化的思想在七年级进行渗透，有助于迁移到今后的学习探究中。

参考文献：

[1]张存敬.第1讲操作性问题[J].中学数学教学参考，2022（3）：51-54.

[2]中华人民共和国教育部.义务教育数学课程标准（2022）版[M].北京：北京师范大学出版社，2022.