小半径弯曲航道整治船模试验及数值模拟研究

蔡创，龚梁爽，杨硕，侯向勇

（重庆交通大学 河海学院，重庆 400074）

1 背景

船舶在内河航道行驶时，有时会遇到弯曲航道，此时船舶的航行会遇到很大的困难，因此对弯道航槽进行船模通航试验及船舶操纵性试验开展模拟研究具有很大的实用性。

湘江是湖南省内的一条非常具有航运价值的河流[1]，水运方面发展有着雄厚的基础。琵琶洲弯道险滩，位于浯溪枢纽库区[1]，它在平面上是典型的回头弯U 型河段。所以，要想在此处确保船舶安全畅通，开展相关自航船模研究十分必要。本文研究的河段主要选取的是琵琶洲急弯河段。

2 船模试验

2.1 船模设计

船模在水中运动时需要满足一定的相似条件[2]。经过量纲分析后，计算出船舶模型的一些重要物理量之间的比尺：

几何比尺：λ=λL=λH=100

时间比尺：λt=λL1/2=10

速度比尺：λv=λL/λt=10

排水量比尺：λΔ=λL3=1000000力的比尺：λf=λL3=1000000

本文船舶模型与实际船舶的有关参数见下表1[3]。

表1 船模与实船参数

船模经过操纵性能率定试验和尺度效应修正后，满足与实船操纵性能相似的试验要求[4]。采用缩小边舵面积的方法[4]，修正后的船舶模型及实际船舶操纵性指数如下表2 所示：

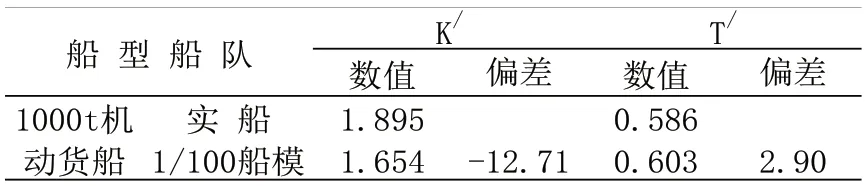
表2 操纵性指数

2.2 试验方案

流量：本论文进行了Q=7550m³/s 的通航试验研究。

航槽布置：

（1）弯曲半径r=360m。

（2）弯曲半径r=440m。

（3）弯曲半径r=480m。

（4）推荐航线，沿缓流区抱凸岸上行、顺江心主流下行。

2.3 船模试验结果及分析

（1）如果船模依照R360、R440 和R480 的布置航槽分别进行航行，船模上、下行的最大舵角都大于25°（见表3)。

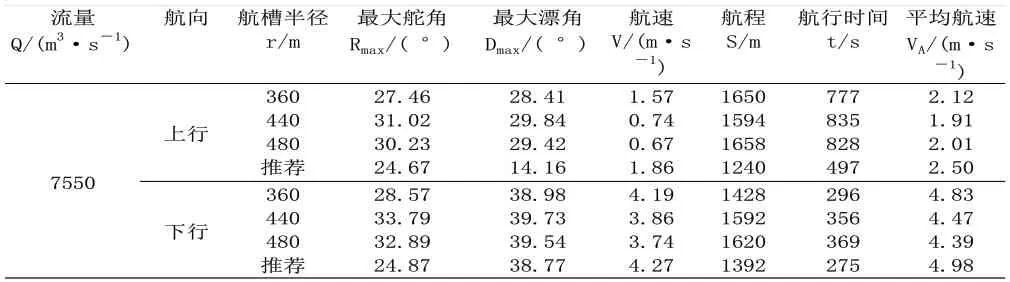
表3 不同航线选择船模试验结果

（2）如果船模选择推荐航槽作为航线，船模上行和下行时的最大舵角值均未超过25°（见表3)，符合安全标准[5]。

3 船舶操纵运动数学模型

3.1 数学模型的建立

（1）MMG 数学模型操纵运动方程

（2）作用在船体上的水动力计算公式

（3）螺旋桨的计算模型

（4）舵的计算模型

3.2 方程求解

船舶操纵运动方程常选择四阶龙格-库塔法[6]来进行求解：

3.3 船舶操纵运动数学模型的检验

根据琵琶洲弯道船舶通航的有关参数，进行船舶操纵运动数学模型的相关检验（图1)：1000t 级货船在静水条件下并满足舵角为25°时，此时定常回转直径达到了3.15L(L 是船长)[7]，符合定长回转直径的规定范围。

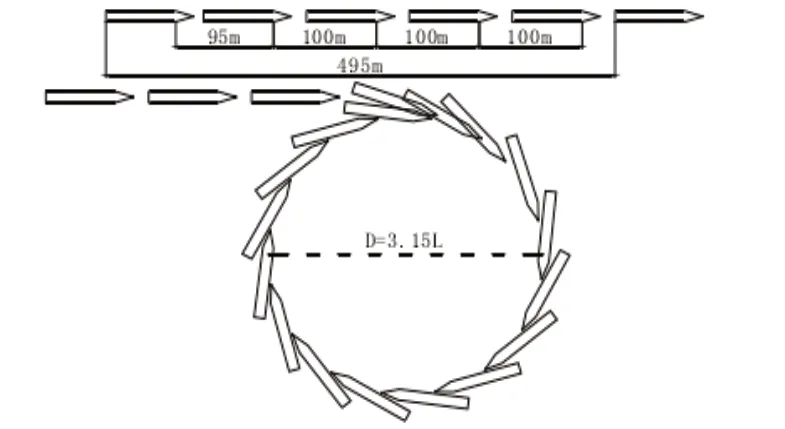
图1 代表船舶推进和回旋性能

4 模型应用及分析

4.1 计算工况

航槽布置：与船模试验航槽布置方案一致

仿真条件：仿真时间、初始船舶速度、初始船舶航向、初始船舶位置、初始水流速度、流向，水深吃水比：深水(见表4）

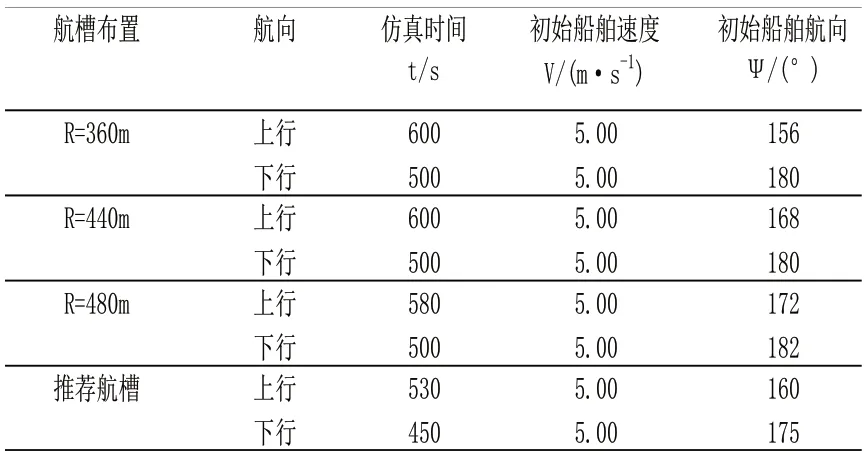
表4 仿真条件

其中：水深吃水比：均为深水；船舶在不同的航线上行时，初始水流速度均为0.2m/s，水流流向为-17°、9°、52°、87°、127°、153°、175°，当船舶在不同的航线下行时，初始水流速度均为0.9m/s，此时水流流向为175°、153°、127°、87°、52°、9°、-17°。

4.2 计算结果与分析

依照布置的四条船舶试验航线，经过仿真计算模拟，得出船舶上行和船舶下行在Q=7550m3/s 流量条件下的试验结果，见表5。

表5 湘江琵琶洲弯道船舶通航试验结果

根据表5 可知：

（1）船舶上行：在Q=7550m3/s 试验流量工况条件下，船舶按照预设的R360、R440 和R480 的固定航槽航行时，最大舵角值不符合安全标准；当船舶按照推荐航线航行时，最大舵角值不超过25°，符合安全标准。

（2）船舶下行：在Q=7550m3/s 试验流量工况条件下，船舶按照预设的R360、R440 与R480 的固定航槽航行时，最大舵角值不符合安全标准；当船舶按照推荐航线航行时，最大舵角值未超过25°，属于安全范围之内。

（3）综合对比，船舶的推荐航线是最良好的一条航线。

5 结论

（1）通过船模试验，可以得知：如果船模按推荐航线行驶时，上、下行最大舵角都在25°范围以内，船模航行安全。所以船模的推荐航线为最佳航线。

（2）本文选择船舶操纵运动数学模型试验来进行有关的仿真模拟计算，可以得知：1000t 自航货船沿着推荐航线行驶时，上、下行的最大舵角值在安全范围之内。很明显，推荐航线就是最优航线。

（3）本文结合船模试验和船舶操纵运动数学模型试验仿真的结果，最终获得一致结论，即船舶的推荐航线为最佳航线。