数学建模方法在施工管理中的应用分析
2023-10-13宫惊立安徽三建工程有限公司建设工程研究院安徽合肥230000
宫惊立(安徽三建工程有限公司建设工程研究院,安徽 合肥 230000)
0 引言
数学作为跨越人生教育十年以上的基础教育学科,其本质是揭示自然界各种量之间的变化关系。数学的诞生和发展就是为了给人类在生产实际中遇到的问题进行解答。随着计算机分析软件的迅速发展,数学建模研究不仅在工程技术、自然科学等领域发挥着越来越重要的作用,而且迅速向经济、管理、金融、生物、医学、环境、地质、人口、交通等各类领域渗透,数学分析技术正在成为重要工具。但另一方面,在建筑施工决策领域,大部分工程管理人员从一开始就失去了对数学的兴趣,认为数学就等于考试,一定程度上阻碍了数学成为建筑企业生产建设决策领域有力分析的工具。
1 浅谈数学建模
所谓数学建模,就是把各类应用题细节化、全面化、现实化,运用量与量之间的变化关系去模拟分析事物的变化规律。数学建模思想方法在各生产制造领域的理论研究已经相当成熟,很多政府层面的政策研究和制定就是建立在数学建模的分析上,但在施工管理决策领域,数学建模思想应用还尚未得到应有的重视。相比BIM 技术的实体建模而言,它是一种虚拟的理论建模分析技术,其本质就是根据各类事物的运行规律去挖掘条件,自己提出问题,定量分析得出一定的最优解决方案,当然这对管理分析者的数学功底和逻辑思维水平提出了较高的要求。全国各理工类高校都有数学建模课程的教学,国家每年也举办数学建模竞赛活动,但数学建模工作似乎只在校园中存在,它往往变成了一种学生装点在校简历的工具,走出校门后很少有人真正坚持把这种思想往生产实践中去探索推广并付诸行动。诚然,要做好这一工作绝非易事,它不但需要长期的理论知识学习积累,还需与具体管理实践相结合,结合建筑施工领域特点,使数学建模可切实地优化生产成本,并为管理决策提供理论层面的指导。
作为工程领域管理者,建模工作的本质仅仅是培养把实际问题翻译为数学语言的能力,现有的文献资料对数学建模在各类工程问题上的理论研究都已比较成熟,但绝大部分都是从纯数学专业角度去介绍建模方法的,公式参数复杂加上语言晦涩难懂,让非数学专业出身的人望而生畏,给实际入门学习带来不小的困难,导致这项具有深刻意义的分析工作无法在实际项目中得到落实推广。下面针对建筑工程中的钢筋下料问题,将其中一些复杂的数学理论本质通俗化、简单化,删去对生产实际无用的繁琐概念,用大众能接受的形式呈现数学建模的用处。
2 钢筋下料成本优化问题
钢筋工程作为建筑主体结构的重要组成部分,其成本造价往往能占到整个项目总造价的三分之一以上,因此对钢筋下料过程加以慎重分析考虑就显得尤其重要,好的决策安排可以做到最大程度地优化材料成本,为企业节省大量不必要的材料浪费,在数学建模领域解决此类问题的知识点被称为多元线性规划(知识点来自运筹学和线性代数)。
2.1 问题定义
钢筋工程大家再熟悉不过,如针对一道梁,根据图纸可以算出此梁所需的各类钢筋工程量(长度),而采购进场的钢筋都有其固定的长度规格(比如9 米定长一根),而配这道梁所需的钢筋有很多种长度,那么这里就存在一个问题,即工人下料钢筋时是怎么拿取原料的。那么有没有一个可行的决策办法做到尽量减少钢筋的浪费?可以这么考虑:例如对一混凝土构件,已算出清单工程量需要1.7m、3.2m、5.5m 和7.6m 四种实际下料长度钢筋各为100 根、80 根、90 根和60根,现场只有足量的定长9m 钢筋,到底最少要多少根定长钢筋可以配好此构件(暂时忽略加工损耗问题)。
每根9m 长钢筋可以被怎样切割利用(使切割后的余料尽可能小),可以把各种切割情况一一列举出来。
下料方案1:每根9m 钢筋用来下料1根7.6m筋,剩下余料1.4m。
下料方案2:每根9m 钢筋用来下料3.2m和5.5m筋各1根,剩下余料0.3m。
下料方案3:每根9m 钢筋用来下料1.7m筋5根,剩下余料0.5m。
下料方案4:每根9m 钢筋用来下料1 根3.2m 筋和3 根1.7m 筋,剩下余料0.7m。
下料方案5:每根9m 钢筋用来下料1 根5.5m 筋和2 根1.7m 筋,剩下余料0.1m。
2.2 建模思路
现在每根9m 钢筋有5 种切割下料选择(实际工程中钢筋种类更多,组合方式种类更复杂),靠人工去一一组合枚举往往无能为力,需要动用分析软件,市面上主流的数学建模分析软件有MATLAB 和LINGO,MATLAB 适用于大型综合问题的编程分析,入门学习和实际推广难度较大这里不做介绍,只讨论LINGO 下面把已列举的下料方案制成表1。
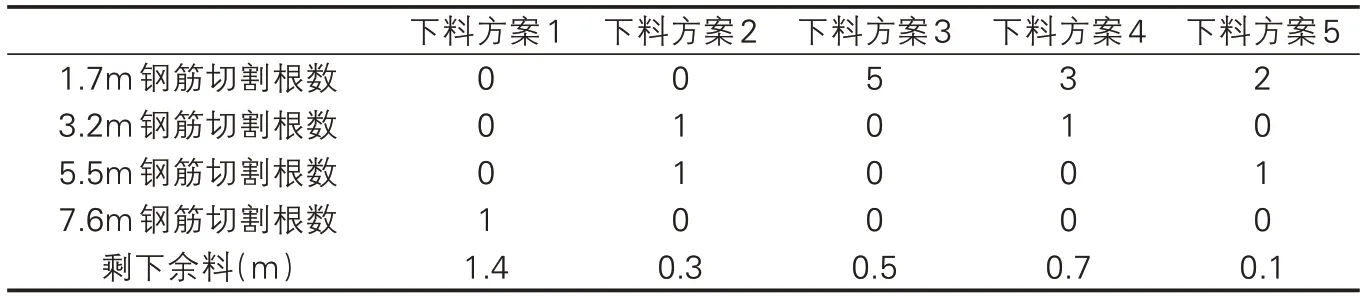
表1 钢筋下料切割方案汇总
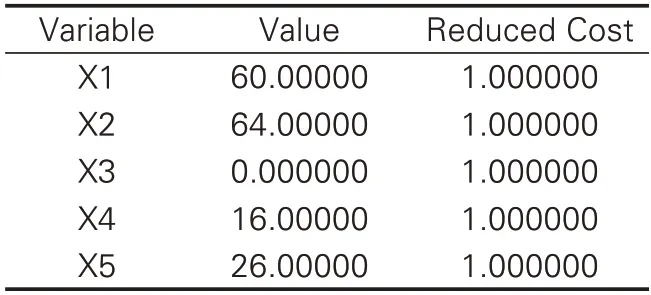
表2 报告部分数据表
在这个问题中,目标是找到满足完成工程量的最少定长钢筋消耗量,而完成工程量所消耗的9m 定长钢筋总量就是这5 种下料方案分别使用的次数总和(称为目标函数),这里设下料方案1-5分别使用的次数分别为x1,x2,x3,x4,x5,即x1+x2+x3+x4+x5。
现在有5 种下料方案,那么每种下料方案各使用多少次(或5 种方案不全用,只用其中的某几个)可完成所需的工作量?这里可以用中小学学过的列方程来表述这一问题,根据所需完成工作量可以列出以下的方程组,
此方程组建立的含义即为所需完成的工程量,1~4 行表示下料方案分别对四种钢筋所生成的总量,例如第一个方程表示5 种下料方案对1.7m 钢筋生成的总量:使用x1次下料方案1会形成0根1.7m 钢筋,使用x2次下料方案2 会生成0 根1.7m 钢筋,使用x3次下料方案3 会生成5 根1.7m 钢筋,使用x4次下料方案4 会生成3 根1.7m 钢筋,使用x5次下料方案5 会生成2 根1.7m 钢筋,而这些使用次数生成的根数总和应不小于1.7m钢筋的所需工程量100 根,后三种钢筋同理。最后行表示这5 类方案使用次数均不为负。
现在这个下料问题就转化成在x1~x5满足上面方程组所列的约束条件下,求表达式x1+x2+x3+x4+x5的最小值。这显然是个五元一次函数求最值问题,若采用笔算则需要数学专业硕士研究生最优化课程相关知识,已经走出校门多年的工程管理者自然没必要再去学习这些较难的理论,有现成的建模计算器来完成结果运算工作。
2.3 利用分析软件进行模型求解
所谓模型求解就是从已找出的各变量约束条件下求出问题答案。对于钢筋这类多元线性规划函数问题,通常使用LINGO 软件进行模型求解(LINGO 专门为求解线性/非线性规划函数最优化问题开发)。
LINGO 对于求解一般线性规划问题容易上手,没有复杂的编程语法语句,基本上和使用计算器输入差不多,打开软件进入输入主界面就可以直接按照数学式的书写样式输入方程组的各行。此问题的输入代码如图1 所示;注意这里是求x1+x2+x3+x4+x5的最小值,称为目标函数放在第一行,前面加上“min=”。代码最后一行的“@gin()”字符串的含义是定义自变量为非负数。输入完毕后点击上方工具栏中的“solve”按钮即可对模型进行求解,结果输出如图2所示,下面将对求解结果文本做一个全面解释。

图2 LINGO12.0模型求解结果报告
2.4 查看求解结果、分析问题
对其结果报告进行分析,并根据报告做出科学合理的管理决策。
结果报告第一行英文意为已找到全局最优解(全局最优解是数学优化分析的专业概念,在钢筋工程优化问题上不必关注)。第二行“Objective value(目标值)”即为建模问题答案,本钢筋下料问题的最优解是完成这一工程量最少需消耗166 根9m 的定长钢筋,也就是在生产实际中任何使用了超过166 根钢筋的行为都必存在不合理的材料浪费,管理者可根据建模求解结果制定现场定量包干包料制度,最大程度的做到节约材料成本。光知道一个结果还不够,还需进一步观察分析各个变量的具体属性。对于钢筋下料工程需重点关注以下部分数据。
前面的Variable 意为全部变量,下面的X1~X5的值即为取得目标最优值时(钢筋消耗最小时)5 个切割下料方案各自的使用次数。后面的Reduced Cost栏数据的实际意义是各变量的取值对目标函数值的影响程度大小,通俗地说就是哪个变量最重要,对建模结果的影响最大。可以看到X1~X5 的Reduced Cost 全为1,说明5 种切割下料方案对建模最终结果的影响程度是相等的,在实际工程中钢筋种类繁多下料方案也更多,各方案的Reduced Cost 值不尽相同,应特别关注那些Reduced Cost值较高的变量,它们往往对问题结果的影响很大,在管理中应予以重视。另外结果中可以看到达到最优解时第3 种下料方案的使用次数为0 且Reduced Cost 值为1,说明这种下料方式不宜采用,而生产实际中这种单独把定长钢筋断为多段小钢筋往往是构件箍筋的下料做法,理论证明这种下料模式达不到钢筋用量的最小化,应采取与其它型号钢筋混合下料的方式。
最后对比一下如果不用数学建模方法,随意采取一个下料方案和建模分析的方案结果有什么不同,假设对1.7m筋,用9m 定长筋下料5 根,总钢筋消耗量为100/5=20 根。对3.2m 和5.5m 筋合并用9m定长筋下料需消耗90根。对7.6m 筋需消耗9m 定长筋60 根。总计消耗20+90+60=170 根,比建模分析的结果(166 根)多消耗4 根,足足36m 长,如果现场实际中再不仔细做好剩余料筋的合理利用工作,仅一个构件就有如此的差距,整个项目整个企业的庞大钢筋工程量造成的消耗差距可想而知。
当然,不管使用什么技术都只是一种辅助手段,最关键的是真正在生产实际中推广落实。像以上的建模问题,要真正落实需要改变钢筋工的下料习惯,并提前说明加上包料监督,这往往需要时间并且存在一定的难度,这对企业的管理水平和力度提出了新的高度要求。
3 结语
目前数学建模在建设施工领域的理论研究成果已经非常广泛,涉及土方工程、现场放线、钢筋下料、塔吊布置、施工方案比选、建设投资预测等很多方面。尤其是钢筋下料问题,其理论背景容易学习理解,并且可和算量软件一样发展为成熟模块化工作。然而这些研究成果很少真正应用在实际项目中。在建筑业市场竞争日益激烈及绿色建造+双碳目标要求日渐严格的环境下,寻求更加科学先进的创新管理方法已成为建筑企业发展的必修课,数学建模研究推广不失为一个非常好的创新发展方向,它更是建筑企业科研项目课题的有力分析工具,建筑企业科研技术部门应予以特别重视,注意培养相关科研人员的数学思维和建模素养。
