考虑风扰的空中机械臂系统力位混合控制
2023-10-13彭定亮郭宇飞李慧子郝志强王志刚
彭定亮,郭宇飞,李慧子,郝志强,王志刚
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.中国舰船研究设计中心,湖北 武汉,430064)
空中机械臂系统主要由旋翼无人机和作业机械臂构成,通常应用于基础设备检测[1-2]、工程辅助[3-4]、生活服务[5-7]等领域。在实施相关作业时,机械臂系统会与外部环境发生物理接触,因此需对其接触力和位置进行精确、有效的控制。机械臂系统与外部环境的物理交互方式可分为准静态接触和动态接触[8]。当机械臂系统相对所接触环境或物体几乎静止时为准静态接触,如物体的抓取[9]和摆放[10],当机械臂系统与所接触环境或物体存在相对运动时为动态接触,如桥梁探伤[1]。
当前,与空中机械臂系统力位控制相关的研究大多针对机械臂系统与外界环境的准静态接触。如Fumagalli等[11]将阻抗控制方法[12]应用于空中机械臂系统的接触式作业控制,借助分级控制结构,将整个系统分为环境系统、无人机系统和机械臂系统等3个子系统并分别设计控制器,研究结果表明,使用该方法既能保证空中机械臂系统的自由飞行稳定性,也能保证其在作业过程中具有较理想的平稳特性。Forte 等[13]利用阻抗控制方法,将空中机械臂系统分为横向、纵向及机械臂等3个控制闭环并分别设计控制策略,同样获得了较好的控制效果。相比之下,与空中机械臂系统动态控制相关的研究较少。孟祥冬等[14]针对空中机械臂系统的动态控制,设计了力位混合控制框架,将整个系统分为2个闭环子系统并对子系统分别进行接触力控制和位置控制,在保证空中机械臂系统平稳移动的同时也能有效控制其接触力。不过,需要指出的是,在已有的研究报道中,无论空中机械臂系统进行准静态接触或动态接触作业,均未考虑不确定风扰因素对机械臂系统整体作业的影响,代波等[15]和Escareo 等[16]涉及风扰因素的研究也仅针对空中机械臂系统中的旋翼无人机部分。为了提升空中机械臂系统在不确定风扰下实施接触作业的控制精度、控制效率和稳定性,本文采用力位混合控制框架[17],将空中机械臂整体系统作业空间分为2个正交子空间并借助比例-微分(PD)加接触力前馈控制方法以及一种固定时间收敛的快速终端滑模控制(FTSMC)方法分别进行接触力控制和位置控制,通过仿真模拟,与采用一般滑模控制(SMC)方法的空中机械臂力位混合控制器[14]控制效果进行对比,以期为风扰条件下的空中机械臂系统力位混合控制研究提供参考。
1 空中作业无人机的动力学模型
1.1 风扰模型
自然风具有突发性、持续性、周期性和不确定性等多种特点,模拟难度极大。粗略建立随机模型来模拟自然风,其风速v由基本风速v1、渐变风速v2和随机风速v3组成[18]。3种风速分别为:
v1=a
(1)
(2)
v3=c·rand(-1,1)sin(2πt+α)
(3)
式(1)~式(3)中,a∈;b∈,t0、t1、t2为时间间隔;c∈,rand(-1,1)为-1到1的随机数。则自然风风速v为:
v=v1+v2+v3
(4)
根据伯努利流体方程,标准风压Pw为:
(5)
式中,r为空气重度,其值为0.01225 kN/m3。
空中机械臂系统在实际风力干扰下的工况极其复杂,此处忽略风扰因素对机械臂控制的影响,仅考虑无人机x,y方向上的二维风,则风扰作用在无人机x、y方向上产生的力Fx和Fy以及力矩Mx和My分别为:
(6)
(7)
式(6)~式(7)中,S为无人机的受风面积,φ和θ分别为无人机环绕x、y轴时的偏转角。此时扰动力矩阵为:
τext=[FxFy0MxMy0 0 0]T
(8)
1.2 风扰下的动力学模型
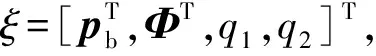
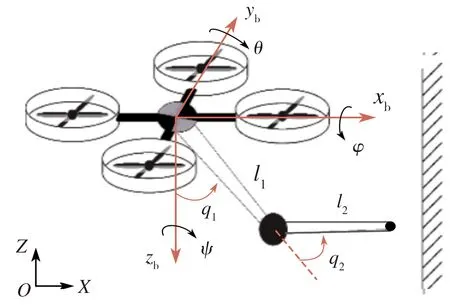
图1 空中机械臂系统示意图
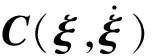
(9)
式中,τ表示系统的驱动力矩,JT表示雅克比矩阵的转置,F表示外界作用于机械臂末端的力,τp表示位置控制系统的驱动力矩,τf表示力控制系统的驱动力矩。本文在考虑风扰对空中机械臂系统控制的影响时,将自然风以扰动力矩阵(式(8))的形式耦合到系统的动力学模型(式(9))中,即风扰因素通过力和力矩作用于系统,这种处理虽然忽略了自然风对机械臂控制的扰动,但因无人机与机械臂之间存在耦合,风扰因素仍会间接影响机械臂的控制。
2 力位混合控制框架
2.1 力位混合控制方案
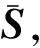

图2 力位混合控制框架
在对空中机械臂系统进行力位混合控制的过程中,欲使系统按照期望的轨迹并获得相应的末端力,需将机械臂部分的关节角位置与工作中的直角坐标相互转换。图3所示为机体坐标系下的机械臂结构图,机械臂在该坐标系下的位置(z1,x1)可表示为:
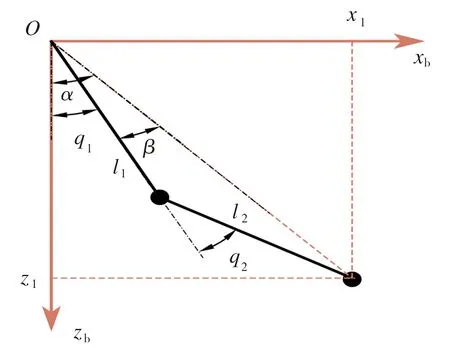
图3 机体坐标系下的机械臂结构
(10)
又有:
(11)
(12)
(13)
由此可得:
(14)
2.2 力控制器设计
机械臂系统力控制采用传统的PD加接触力前馈控制方法。根据胡克定律,机械臂系统与外部环境接触时的测量力F为:
(15)
式中,K为环境刚度。基于图3,可以求出该机械臂的雅克比矩阵J为:
(16)
将机械臂末端所受实际力F与相应期望力Fd进行比较,从而实现力的闭环控制。借助机械臂转置雅可比矩阵JT,可将机械臂工作空间中的力转化为各关节上的驱动力。故驱动力力矩τf=JTF。
2.3 位置控制器设计
2.3.1 固定时间收敛系统
引理1[21]考虑一类非线性系统:
(17)
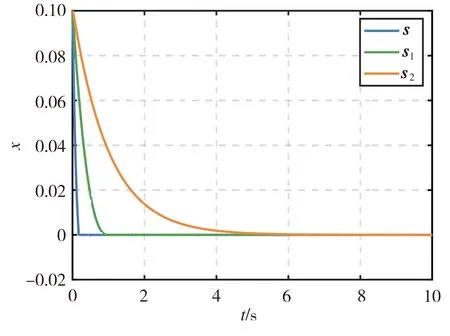
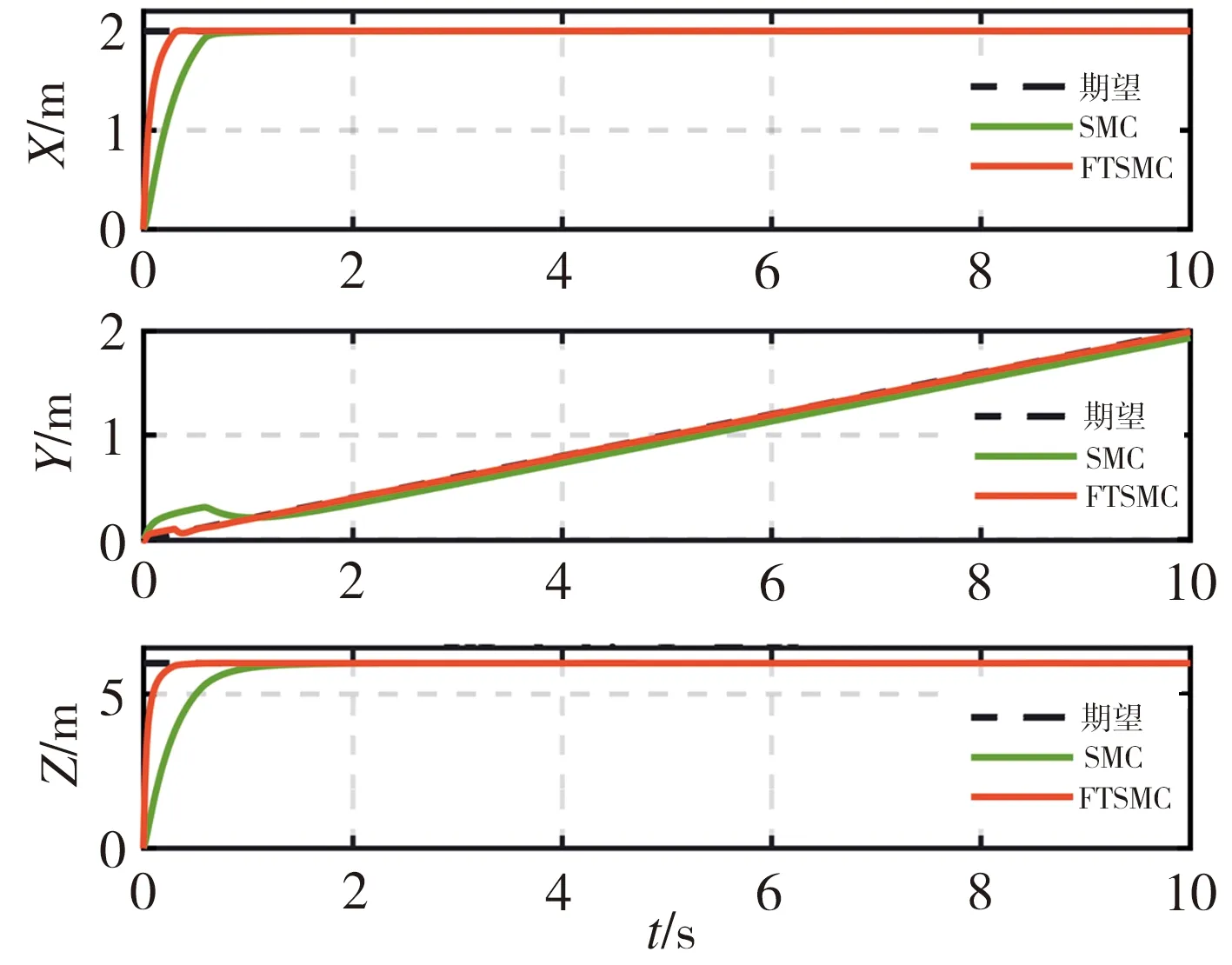
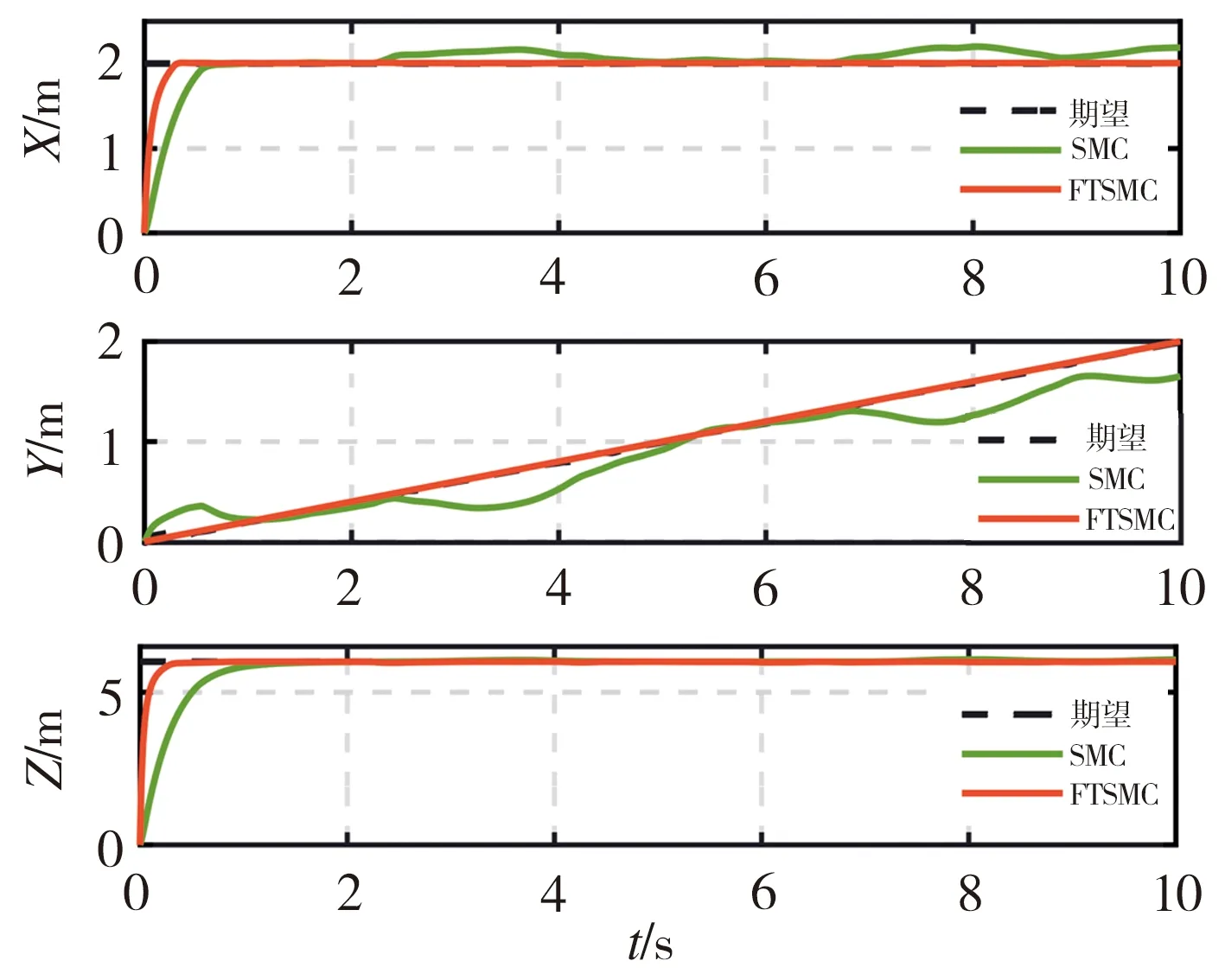
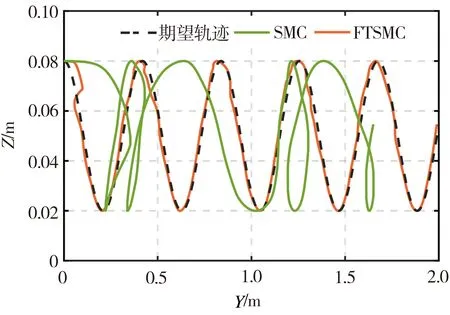
式中,signa1y=|y|a1sign(y),b1>0,b2>0,a1>1,0 (18) 该式中的控制系统收敛时间上界Tmax可通过选择不同的参数a1、a2、b1、b2来确定,并不需要依赖系统初始状态。Zuo等[22]根据这种非线性系统设计的固定时间收敛的滑模控制方法取得了良好的应用效果,但在收敛的速度上还有进一步改善的空间。姚来鹏等[23]设计了一种固定时间收敛的终端滑模控制器并应用于弹药传输机械臂中,其研究结果表明,该方法对不确定干扰具有强鲁棒性,能够对外界扰动下的弹药传输机械臂进行准确定位控制。 2.3.2 基于固定时间的快速终端滑模控制器设计 (19) s=e2+Asignk1(e1)+Bsignk2(e1) (20) 式中,A、B为对称矩阵,k1>1,0 -α1sign(s)α2|s|β1sign(s)-α3|s|β2sign(s)] (21) 式中,α1、α2、α3均大于0,0<β1<1,β2>1。通过分析可知,式(20)滑模面具有收敛特性。当系统状态距平衡点较远时,Asignk1(e1)起主导作用,保证系统快速收敛;当系统接近平衡点时,Bsignk2(e1)起主导作用,保证系统在固定时间内稳定,使系统在整个过程中保持较快的收敛速度。 基于引理1给出的固定时间Ts,对式(9)所示的系统动力学方程采用式(20)所示的滑模面以及式(21)所示的控制律,则系统误差在固定时间内收敛至平衡点,收敛时间T满足: T (22) Bk2diag(|e1|k2-1)e2] =sT[-α1sign(s)-α2|s|β1sign(s)- α3|s|β2sign(s)] ≤sT[-α1|s|-α2|s|β1-α3|s|β2] ≤-α2|s|β1+1-α3|s|β2+1 (23) (24) 由上分析证明可知,系统状态可从任意位置到达滑模面s→0。然后沿着滑模面做趋近运动至平衡点的一个极小邻域内震荡,理想的滑动模态满足: (25) 考虑Lyapunov函数为: (26) 对其求导得: (27) 系统状态在固定时间t2内收敛,即: (28) 综合可得,收敛时间为:T=t1+t2≤Tmax=T1+T2。 对本研究采用非奇异固定时间终端滑模面的优越性进行验证。选取一般滑模面s1和传统非奇异终端滑模面s2进行仿真对比。一般滑模面为: s1=σ1e1+e2 (29) 式中,σ1∈。传统终端滑模面为: s2=σ2e1+σ3signr(e2) (30) 式中,σ2、σ3、r∈。为了便于对仿真结果进行对比,相关参数的取值依次为:σ1=σ2=σ3=1;A=diag([1 1 1 1 1 1 1 1]);k1=3/5;B=diag([20 20 20 20 20 20 20 20]);k2=5/3。则本研究所采用的具有固定时间收敛的快速终端滑模面可表示为: s=e2+Asignk1(e1)+Bsignk2(e1) (31) 选用不同的滑模面,分别在初始状态x(0)为0.1和10时进行仿真模拟,结果如图4所示。由图4可见,无论系统初始状态是在平衡点附近还是远离平衡点处,与采用滑模面s1和s2相比,采用固定时间收敛的快速终端滑模面s明显提高了系统状态的收敛速度,该仿真结果充分证实了采用滑模面s的优越性。 (a)x(0)=0.1 表1 空中机械臂系统主要参数 不考虑外界干扰即τext→0。此时,将位置控制系统中期望位置与实际位置的差值作为反馈信号。根据图1所示的空中机械臂系统结构及仿真设定的期望值可知,对空中机械臂系统进行位置控制时,要求在旋翼无人机向 轴方向移动的同时,由机械臂末端来完成轨迹跟踪和接触力控制。图5和图6所示分别为无外界干扰条件下无人机的位置、姿态以及机械臂末端轨迹的仿真模拟结果。通过分析图5中无人机在X、Y、Z方向上的位置和姿态角变化可知,采用FTSMC方法对空中机械臂系统进行位置控制时,无论在控制精度还是响应速度上均较采用SMC方法时有明显提高,并且图6的仿真结果同时表明,所采用的FTSMC方法在机械臂末端轨迹跟踪方面也有更好的表现。 (a)位置变化 在对空中机械臂系统进行接触力控制时,选择PD控制器和接触力前馈控制来实施对期望力的控制,该控制器将实际接触力与相应期望力的差值作为反馈信号。虽然位置控制系统和力控制系统分开控制,但整个空中机械臂系统是耦合关系,相互会产生影响。无外界干扰条件下,机械臂系统接触力控制的仿真模拟结果如图7所示。由图7可见,随着系统位置控制精度的提升以及响应时间的延长,系统接触力的控制效果也相应提高。 对式(4)所描述的随机自然风进行模拟,结果如图8所示。 在风扰条件下,分别采用FTSMC控制器和SMC控制器对空中机械臂系统进行位置控制,旋翼无人机的位置、姿态以及机械臂末端轨迹的仿真模拟结果分别如图9和图10所示。由图9和图10可见,无论对于无人机的运动轨迹还是机械臂末端执行器的运动轨迹,采用FTSMC控制器在控制精度和响应速度上均比采用SMC控制器时有明显提升,并且采用FTSMC控制器对外界风扰的抗干扰能力也更强。 (a)位置变化 图10 风扰下的机械臂末端轨迹 (1)应用力位混合控制框架将机械臂系统位置控制和接触力控制分解成相互正交的两部分,并分别借助传统的PD加接触力前馈控制和FTSMC进行接触力控制和位置控制。 (2)应用力位混合控制器能够有效抑制风扰的影响,在风扰下实现了对空中机械臂系统的力及位置进行同时控制。 (3)与SMC控制器相比,FTSMC控制器在控制速度/控制精度和抗干扰能力等方面均有明显提升,具有良好的鲁棒性。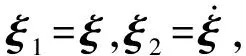
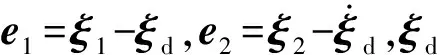
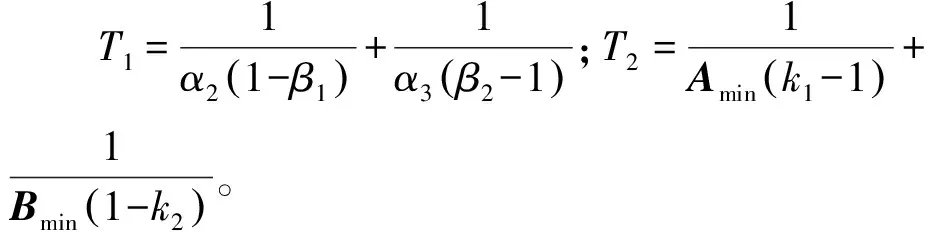
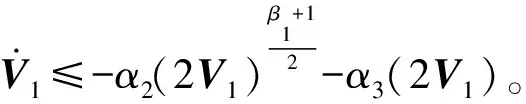
3 机械臂系统力位混合控制仿真分析


3.1 不考虑外界干扰时的仿真结果
3.2 考虑外界风扰的仿真结果
4 结论
