基于GASA-BP的轧辊内部缺陷检测方法

2023-10-13陶海然郭钰瑶张泽琳夏绪辉

武汉科技大学学报 2023年5期

王蕾,陶海然,郭钰瑶,张泽琳,夏绪辉

(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北武汉,430081)

轧辊是轧机的核心部件,直接影响轧机生产效率和产品质量,因此必须对轧辊的各种缺陷进行全面监测。轧辊的表面缺陷可以通过肉眼或机器视觉进行识别,但其内部缺陷无法直接辨别。轧辊内部缺陷主要有裂纹、夹杂、气孔等类型[1],为了不对轧辊自身造成损伤,工业中常用无损检测方法来确定其内部是否存在缺陷[2]。超声检测是一种常规无损检测方法,为了提高超声检测信号的识别精度,研究人员探讨了各种改进措施。唐东林等[3]提出基于比值加权最小误差平方和的判别函数(RWESOS)并应用于变量预测模式识别方法(VPMCD),在对不同缺陷大小的超声检测信号识别中,该方法的识别率比BP 神经网络和采用普通判别函数的VPMCD 方法的识别率分别提高了4%和11%。顾桂梅等[4]针对棒式绝缘子表面缺陷识别问题,采用改进遗传算法优化BP 神经网络(GA-BP),并搭建Opencv仿真实验平台验证了GA-BP的有效性。潘峰等[5]通过经验模态分解(EMD)对管道腐蚀缺陷的超声信号进行时域特征参数提取,并采用PSO-SVM模型来提高缺陷分类效果,实验结果显示该方法对不同深度管道腐蚀缺陷的识别准确率可达到87.5%。Lei等[6]针对平板陶瓷薄膜进行超声检测,采用经过误差补偿的CNN模型识别缺陷信号,识别准确率达到95.63%。Liang等[7]将IAFSA-SVM模型用于井控多管阀的管道超声缺陷识别,通过小波包分解获得信号的特征向量,采用支持向量机和改进人工鱼群算法共同优化参数,实验证明该模型对不同深度的超声信号可达到94.67%的识别率。Pan等[8]提出一种基于多特征融合和多准则特征评价的缺陷识别模型,通过分析超声回波信号数据,采用多种特征提取和融合方法,应用支持向量机(SVM)进行缺陷信号分类,融合D-S证据理论确定最终分类结果,该模型对管道缺陷的识别准确率达到96.29%。

在现有研究的基础之上,本文采用模拟退火算法(SA)优化GA-BP网络模型(记为GASA-BP),对轧辊内部超声检测信号进行缺陷识别。GA算法具有很强的全局搜索能力,但其局部搜索能力相对较弱,通过SA算法优化GA-BP网络模型,能避免GA算法陷入局部最优,并使BP网络模型收敛更快,得到更精确的输出值。本文方法首先要进行信号预处理,采用自适应灰狼优化阈值法(记为AGWO-WT)确定最优的小波阈值后对原始检测信号去噪,然后分别采用三层、四层、五层小波包变换法提取去噪信号的能量特征,最后通过GASA-BP网络模型对所提取的能量特征向量进行分类训练,实现轧辊内部缺陷类型的识别。

1 轧辊内部超声检测信号的分类识别

本文提出的轧辊内部超声检测信号分类识别方法如图1所示。

1.1 基于AGWO-WT的信号预处理

进行轧辊超声波探伤检测时,仪器本身(探头、超声波探伤仪等)会产生杂波信号[9],为消除该部分信号对轧辊内部缺陷识别的影响,需要进行降噪处理。首先对信号进行多尺度小波分解,然后通过AGWO-WT获得最优小波阈值并完成信号去噪,最后对去噪信号进行小波包分解,提取其能量特征。

灰狼算法是受自然环境中灰狼狩猎行为的启发而提出的一种群智能优化算法,其主要特点是狼群按适应度值分为四个层级(首领狼α、协助狼β、听从狼δ、底层狼ω),底层狼ω的数量最多,能够按照上三层狼的命令进行包围、追捕、围剿猎物,用数学式描述狼群包围狩猎的行为,如式(1)和式(2)所示:

D=|2r2·Xp(t)-X(t)|

(1)

X(t+1)=|Xp(t)-(2a·r1-a)·D|

(2)

式中:Xp(t)和X(t)分别代表猎物和狼群的位置;t为狼群位置当前更新的次数;a为收敛因子,其模随t的增大从2线性衰减至0;r1和r2为分量取值在[0,1]区间的随机数向量。

狼群在成功包围猎物后开始靠近猎物,α、β、δ的位置更新公式如下:

(3)

其中

(4)

式(3)～式(4)中:X1、X2、X3分别代表最优三只狼α、β、δ的更新位置;Xα、Xβ、Xδ分别代表α、β、δ的当前位置;Dα、Dβ、Dδ分别代表灰狼个体与α、β、δ的距离;C1、C2、C3分别代表α、β、δ的协同系数向量C;A1、A2、A3分别代表α、β、δ的协同系数向量A。

狼群位置最终由α、β、δ更新后的位置共同决定,如式(5)所示:

(5)

AGWO-WT的基本原理是采用灰狼算法获取最优的小波去噪阈值,其主要通过梯度下降的方法来更新阈值ε[10]:

ε(n+1)=ε(n)+μΔε(n)

(6)

式中:n为梯度下降次数,μ为梯度下降步长,Δε(n)的取值如式(7)所示。

(7)

式中:yi为检测信号的第i个分量;gi为函数估计表达式,这里引入Sigmoid函数作为阈值函数,因此有

gi=φ(dj,i,ε)-dj,i=

(8)

式中:φ(dj,i,ε)为阈值函数,dj,i为j尺度上的小波分解系数,η的取值一般为2。

基于AGWO-WT的轧辊内部超声检测信号预处理的具体步骤如下:

1)对原始超声检测信号进行多尺度小波塔式分解,获取轧辊超声检测信号低频和高频分量及各尺度的小波系数。

2)对于高频系数,应用AGWO-WT获取最优阈值。设定灰狼算法的初始参数,如搜索维度、狼群数量、最大迭代次数、搜索范围等。

3)根据式(6)确定狼群个体适应度,以Δε(n)值作为寻优依据,当Δε(n)最小时,保存当前最好的三个个体作为上三层狼。

4)狼群按式(3)和式(4)接近猎物,按式(5)更新位置。

5)判断迭代是否满足约束条件(达到设定的误差值或迭代次数等),是则结束捕猎并输出最优的小波阈值,否则重复执行步骤3和步骤4。

6)根据步骤5获取的最优阈值修改小波高频系数,得到修改后的高频信号,再与低频信号进行小波塔式逆重构,实现超声检测信号去噪。

7)对去噪后的轧辊检测信号分别进行三层、四层、五层小波包分解。利用有缺陷和无缺陷轧辊的子节点能量差值来构建检测信号能量特征向量Vd的分量Tpq,具体计算如式(9)所示,进而完成轧辊超声检测信号的预处理。

(9)

(10)

1.2 基于GASA-BP网络的轧辊缺陷识别

一般的BP神经网络模型包含由两组权重因子连接的输入层、隐含层和输出层,通过调节权重因子来增强或者减弱该层神经元所占比重,如图2所示。本文按照误差梯度下降法来调整各层的权值和阈值,如式(11)和式(12)所示,通过对数据样本的训练,保留模型误差最小的权值和阈值。其过程分为:数据信号正向传播时,经过隐含层并在输出层映射出结果;数据信号反向传播时,误差数据经过隐含层并在输入层按式(13)计算模型的误差值。

图2 BP神经网络模型

(11)

(12)

式中:θj代表隐含层中第j个神经元的阈值,bm代表输出层中第m个神经元的阈值。

(13)

式中:Ym(n)、Pm(n)分别表示输出层中第m个神经元的输出值和目标值。

GA-BP算法[11]利用遗传算法优化BP神经网络的主要参数,以BP模型的输出误差之和(式(14))作为GA的适应度函数,通过适应度值对染色体进行筛选,适应度越小则染色体越优。

(14)

GA算法的不足之处是其局部搜索能力较差,为此将SA算法引入GA-BP模型[12],根据Metropolis准则决定是否接收GA算法获得的最优解,利用SA在局部搜索方面的优势来减小GA陷入局部最优的概率。

采用GASA-BP模型对轧辊内部超声检测信号进行缺陷识别的主要过程分为三部分:GASA-BP模型的初始参数设置、GASA优化BP网络的权值和阈值、不同轧辊类型的能量特征分类训练及测试。具体步骤如下:

1)将小波包算法提取的轧辊超声检测去噪信号能量特征作为BP神经网络的初始输入参数,并进行数据归一化处理。为提高GASA-BP模型的识别成功率,根据式(15)确定BP神经网络隐含层的最佳神经元个数。

(15)

式中:I、J、M分别为输入层、隐含层、输出层的神经元个数,γ为1～10之间的整数。

2)确定BP、GA、SA算法的初始化参数。依据BP的初始化参数确定GA和SA的初始化参数,如GA的种群规模、SA的初始及终止温度、终止算法的约束条件等。

3)对遗传算法中的染色体进行选择、交叉、变异,根据式(14)计算个体适应度值。

4)进行模拟退火操作。根据步骤2中设定的初始温度、终止温度等参数,按Metropolis准则(见式(16))对步骤3中的染色体适应度值进行更新,获得最优染色体。

(16)

5)若满足SA算法约束条件(迭代次数、误差等达到设定值),则将最优染色体作为BP神经网络的初始权值和阈值;否则继续执行步骤4。

6)在确定好的BP神经网络结构中,以归一化后的能量特征值作为神经网络的训练样本进行训练,使用Levenberg-Marquardt 方法来加快BP网络的训练速度,并根据式(14)计算单个样本的输出误差。

7)若满足BP网络模型约束条件(迭代次数、误差等达到设定值),设定神经网络的权值和阈值,在神经网络的输出层得到计算值,据此判断轧辊内部缺陷的类型;否则继续调整神经网络的权值和阈值,重复步骤6。

2 实验结果及分析

实验数据为自采集的轧辊内部超声检测信号,实验装置包括PXUT-330N型数字超声波探伤仪、双晶直探头DA5P14FS25、若干直径为63.8 mm的轧辊试件以及数字化通讯系统软件等。探伤仪校准及对不同轧辊试件进行超声信号采集如图3所示。获得轧辊检测信号共400组,包含轧辊内部气孔缺陷信号80组、轧辊内部不同夹杂缺陷信号110组、轧辊内部裂纹缺陷信号110组、轧辊内部无缺陷信号100组。本文数据预处理及模型训练等主要采用MATLAB软件。

2.1 轧辊内部超声检测信号预处理

首先通过OriginPro软件将轧辊超声检测信号数据化处理,采样点数设为64,随后进行小波阈值法降噪,最后进行小波包分解,本节以四层小波包分解为例进行分析。综合现有文献,从Daubechies、Symlets和Coifets三类小波基中选取一种最适合本文研究对象的小波函数。修改高频信号阈值时,通过AGWO-WT算法(初始参数设置见表1)寻找最优阈值,并与应用较多的无偏风险估计软阈值法、启发式软阈值法、极大极小软阈值法进行去噪效果对比。随机抽取10组轧辊超声检测数据,不同的小波基和小波阈值法所对应的去噪效果如图4和图5所示。对比图4中10组检测数据的去噪效果后,本文选取的最优小波基为sym7。由图5可见,本文提出的AGWO-WT方法要明显优于对比阈值法。

表1 AGWO-WT算法的初始参数

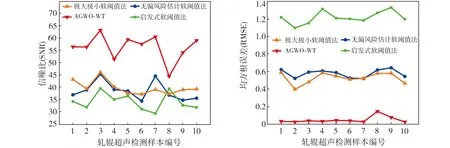
(a)10组轧辊检测信号的信噪比 (b)10组轧辊检测信号的均方根误差

对轧辊超声检测信号数据进行处理后,得到归一化后的轧辊内部无缺陷以及有气孔、裂纹、夹杂等缺陷情况下的去噪信号,如图6所示。分别采用三层、四层、五层的小波包分解,提取出信号去噪后的能量特征值。为提高轧辊超声检测数据的利用效率,按式(9)计算其小波包分解得到的子节点能量特征值,并进行归一化处理,结果如图7所示。

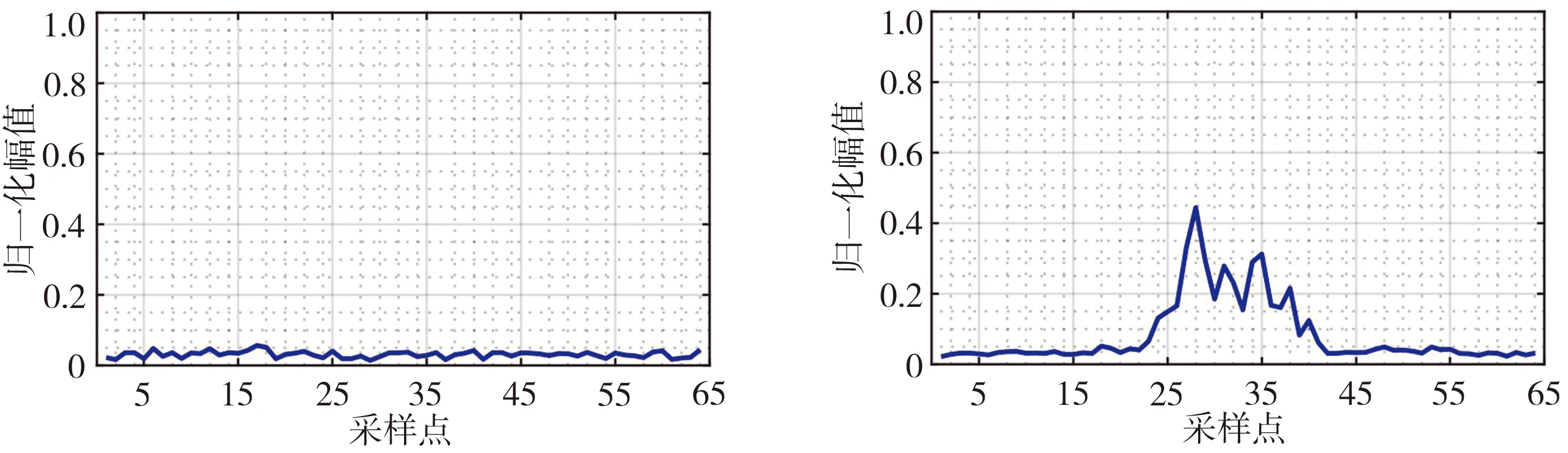
(a)轧辊内部无缺陷 (b)轧辊内部有夹杂

(a)三层小波包分解 (b)四层小波包分解 (c)五层小波包分解

2.2 轧辊内部缺陷的识别

实验过程中,从300组轧辊内部有缺陷的样本数据中随机抽取270组作为训练样本,剩下的30组作为测试样本。采用传统BP神经网络模型和本文提出的GASA-BP网络模型进行对比分析,以小波包分解所得轧辊超声检测去噪信号的能量百分比向量作为两个模型的输入。模型输出层的向量维度为3,将其元素最大值置1,其余值置0,故输出向量可能为[1 0 0]、[0 1 0]或[0 0 1]。用输出向量与列向量[1 2 4]T相乘,得到最终识别结果:结果为 1代表轧辊内部有夹杂,结果为2代表轧辊内部有裂纹,结果为4代表轧辊内部有气孔。

依据BP神经网络初始参数的多次调试结果来确定GA和SA的初始化参数,GASA-BP算法的初始参数设置见表2。输入层的神经元个数由小波包分解层数来决定,三层、四层、五层小波包分解所构建的能量特征向量的维度分别为8、16、32,因此输入层的神经元个数也分别为8、16、32。按式(15)确定隐含层神经元个数取值范围,采用MATLAB进行仿真计算,寻找出最佳的隐含层神经元个数。以五层小波包分解为例,不同隐含层神经元个数的结果对比如图8所示,可以确定最佳的BP、GASA-BP神经网络结构分别为32-7-3、32-12-3。

表2 GASA-BP算法的初始参数

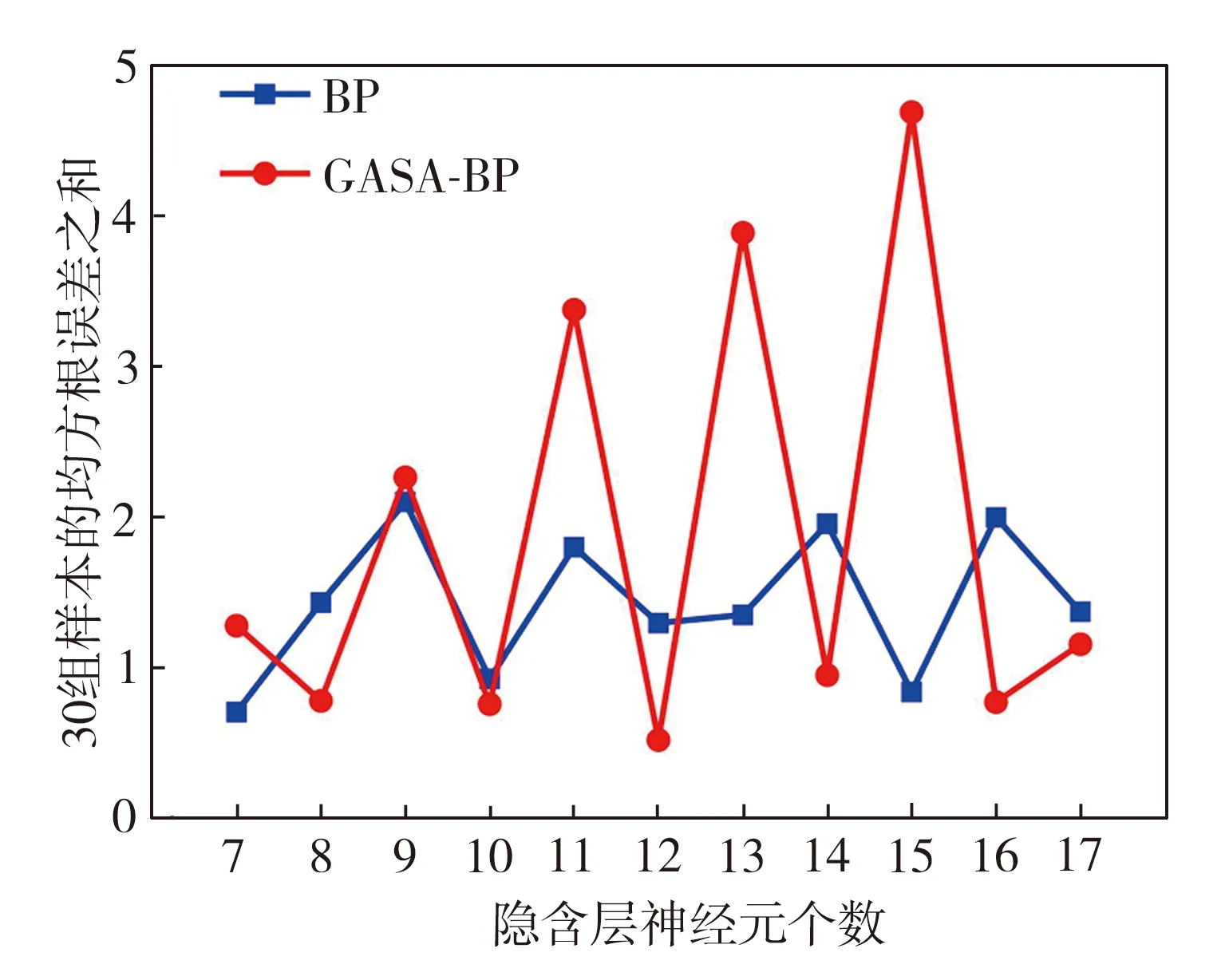
图8 不同隐含层神经元个数的结果对比

2.3 轧辊内部缺陷识别结果分析

对原始信号分别进行三层、四层、五层小波包分解,根据预处理后的数据采用BP和GASA-BP网络模型进行轧辊缺陷识别,其中,基于五层小波包分解所构建特征向量的识别结果及误差(根据式(14)计算)如图9所示,训练样本的误差变化曲线如图10所示。鉴于模型运行结果会有一定的随机性,同时为减少模型训练出现过拟合而对识别结果产生不利影响,让每个模型运行14次,去掉识别准确率最好的2次和最差的2次,取其余10 次运行结果的平均值,不同模型对30个测试样本的识别成功率如表3所示。

表3 不同模型对30个测试样本的识别准确率

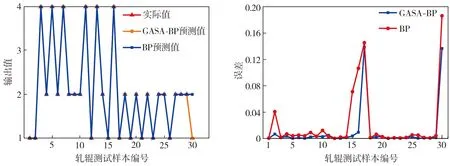
(a)预测结果 (b)预测误差

(a)BP神经网络训练误差 (b)GASA-BP网络训练误差

结合图10和表3进行分析,BP神经网络模型的平均识别准确率为91.97%,迭代5 000次后也没有使模型误差降到10-3,耗时7.618 s;运用改进的神经网络模型GASA-BP进行轧辊缺陷识别,平均识别准确率为95.06%,迭代次数仅为17次,耗时0.455 s,收敛速度约为BP神经网络模型的15倍,识别准确率提高了3.09个百分点,且在网络训练的第9次,误差就已降到10-10。

由表3还可以看到,采用三层、四层、五层小波包分解构建能量特征向量,GASA-BP模型识别准确率都在93%以上,且随着分解层数的增加,识别准确率不断增加,其中,五层小波包分解对应的模型识别效果最好。但另一方面,采用该模型识别三层、四层、五层小波包分解构建的能量特征向量时,所需要的时间分别为0.215、0.358、0.455 s,即小波包分解层数越多,特征向量的维度就越大,模型的收敛时间也就越长。

综上所述,本文构建的GASA-BP模型可应用于轧辊内部缺陷识别,且能在一定程度上满足大部分企业对轧辊缺陷分类精度及效率的要求。