面向复杂空间路径的焊接机器人运动学分析与轨迹规划
2023-10-13任豪豪秦庆平
余 震,任豪豪,秦庆平,胡 柯
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081;3.通标标准技术服务(青岛)有限公司,山东 青岛,266101)
焊接机器人不仅能减轻焊工的劳动强度,还能提高焊接质量与效率[1]。随着智能制造技术及智能装备的发展,复杂零部件的焊接对机器人焊接技术提出了更高的要求。在复杂空间结构焊接过程中,需要不断调整焊枪的位姿以跟随焊缝空间位置变化,如何提高复杂空间路径焊接工件的焊接质量是目前机器人焊接路径规划及焊接运动学研究的方向之一。
关于焊接机器人运动学模型构建和运动学分析的研究成果有不少。朱志明等[2]针对箱型钢结构特征和焊接特点设计了一款五自由度焊接机器人,通过建立的机器人模型推导出焊接机器人各关节变量的解析关系模型,然后对于给定轨迹利用MATLAB进行了仿真分析。程晓飞[3]针对管-管相贯线焊缝设计了一款四自由度焊接机器人,建立了简化的机器人连杆坐标系,推导出机器人焊枪的姿态方程。李向春等[4]为了实现一定范围管径的相贯线焊缝的自动化焊接,通过Pro/Engineer建立五自由度相贯线焊接机器人模型,并推导出模型正逆解。上述研究中的焊接机器人均为专机结构,机器人自由度较少,研究成果对工业上常用的六自由度焊接机器人的适用性不强。宁青杰等[5]以SR165焊接机器人为研究对象进行建模,通过MATLAB中的Robotics Toolbox对机器人手腕末端进行工作空间云图、角位移、角速度和角加速度仿真。冯树先等[6]建立了ABB IRB140型焊接机器人的三维模型,通过Robotics Toolbox对机器人进行点到点和连续轨迹的规划。刘蕊等[7]通过正运动学分析得出焊接机器人的运动学方程,进行逆运动学求解后得到每个关节的函数表达式,进而根据表达式提出求解机器人末端位置所有精确值的算法。何佳斌等[8]针对Motoman-UP6型弧焊机器人建立正运动学模型,利用MATLAB建立马鞍形焊缝坐标系并求得机器人逆运动学解。熊思淇等[9]以ABB IRB1600型焊接机器人为研究对象,利用MATLAB分析其正运动学、逆运动学和轨迹规划问题。这几位研究者在逆运动求解过程中并没有充分讨论解的存在情况,忽略了机器人的奇异位置,求解过程中可能会得到机器人逆运动学的伪解。
对于进行复杂空间路径焊接的机器人来说,其自身结构和关节布置方式的不同增加了机器人运动学分析的复杂度,不同机器人的正逆运动学求解方式也各不相同。本文以ABB集团的IRB 1410型焊接机器人为研究对象,通过改进的D-H参数法(Modified Denavit-Hartenberg,MDH)建立焊接机器人的运动学模型,推导焊接机器人末端相对于基坐标系的位姿变换矩阵,得到焊接机器人逆运动学的解析解,同时设计焊接机器人的逆运动学算法流程,得到机器人逆运动学全部解。由于管-管相贯形成的马鞍形焊缝的坡口角度会随着空间位置的不同而改变,在马鞍形焊缝回转线上的焊缝角度和深度在各个空间位置也不相同,因此本文通过建立的运动学模型,对马鞍形复杂空间焊缝进行等角度插补轨迹规划,经过五次多项式插值对焊接轨迹进行衔接,分析焊接机器人沿轨迹运动的参数变化,以期为面向复杂空间路径的焊接机器人工业应用提供理论依据。
1 焊接机器人空间模型的构建
IRB 1410焊接机器人由连杆和6个转动关节(见图1)串联而成,通过MDH法在各连杆近端建立关节坐标系[10](见图2)。采用连杆长度a、连杆转角α、连杆偏距d和关节转角θ这4个参数构建各连杆间的位姿方程。

图1 IRB 1410机器人的结构图
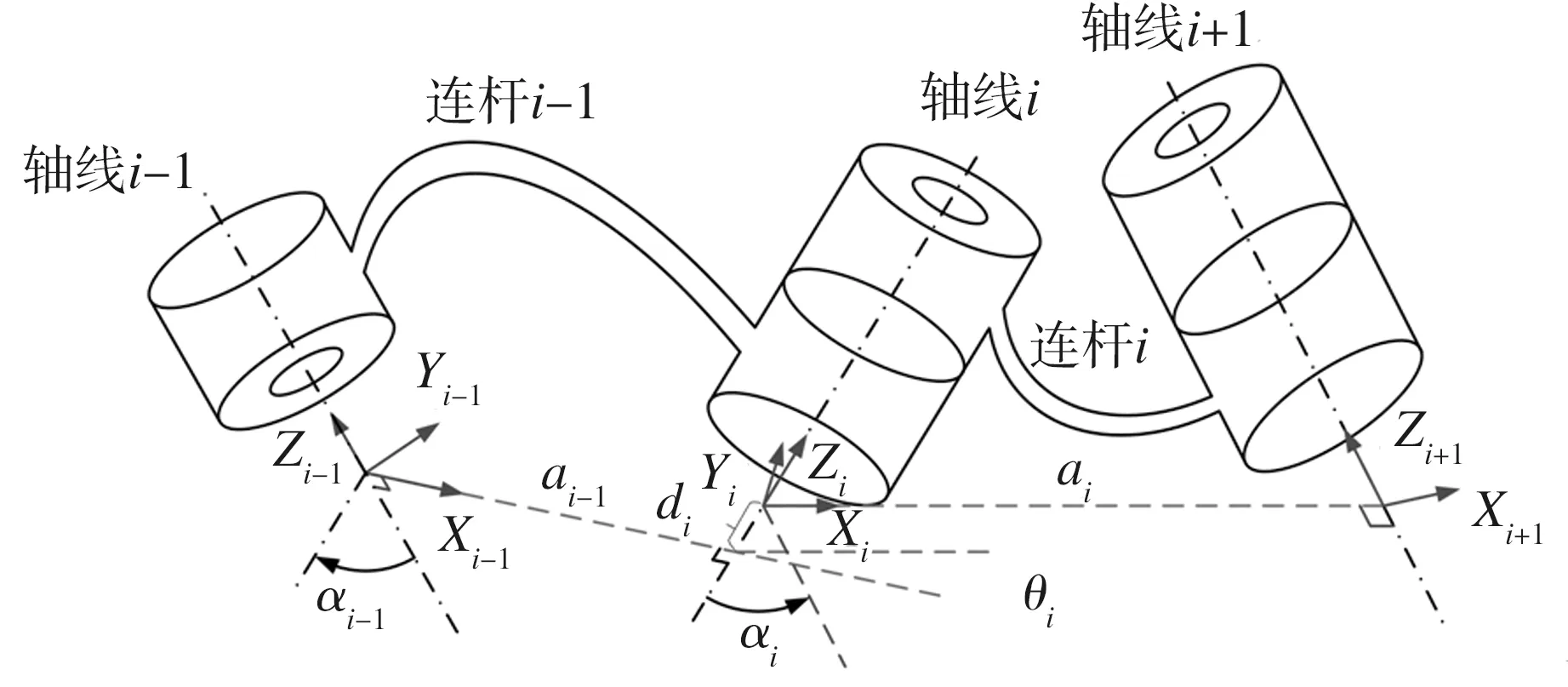
图2 采用MDH法建立的关节坐标系

(1)
式中:RXi-1(αi-1)、RZi(θi)均为旋转变换矩阵,DXi-1(ai-1)、DZi(di)均为平移变换矩阵。矩阵表达式为:
作为六自由度关节型机器人,IRB 1410机器人的6个关节均为旋转副,采用MDH法根据机器人结构尺寸(如图3所示)建立连杆坐标系(如图4所示),MDH参数见表1。

表1 IRB 1410机器人MDH参数
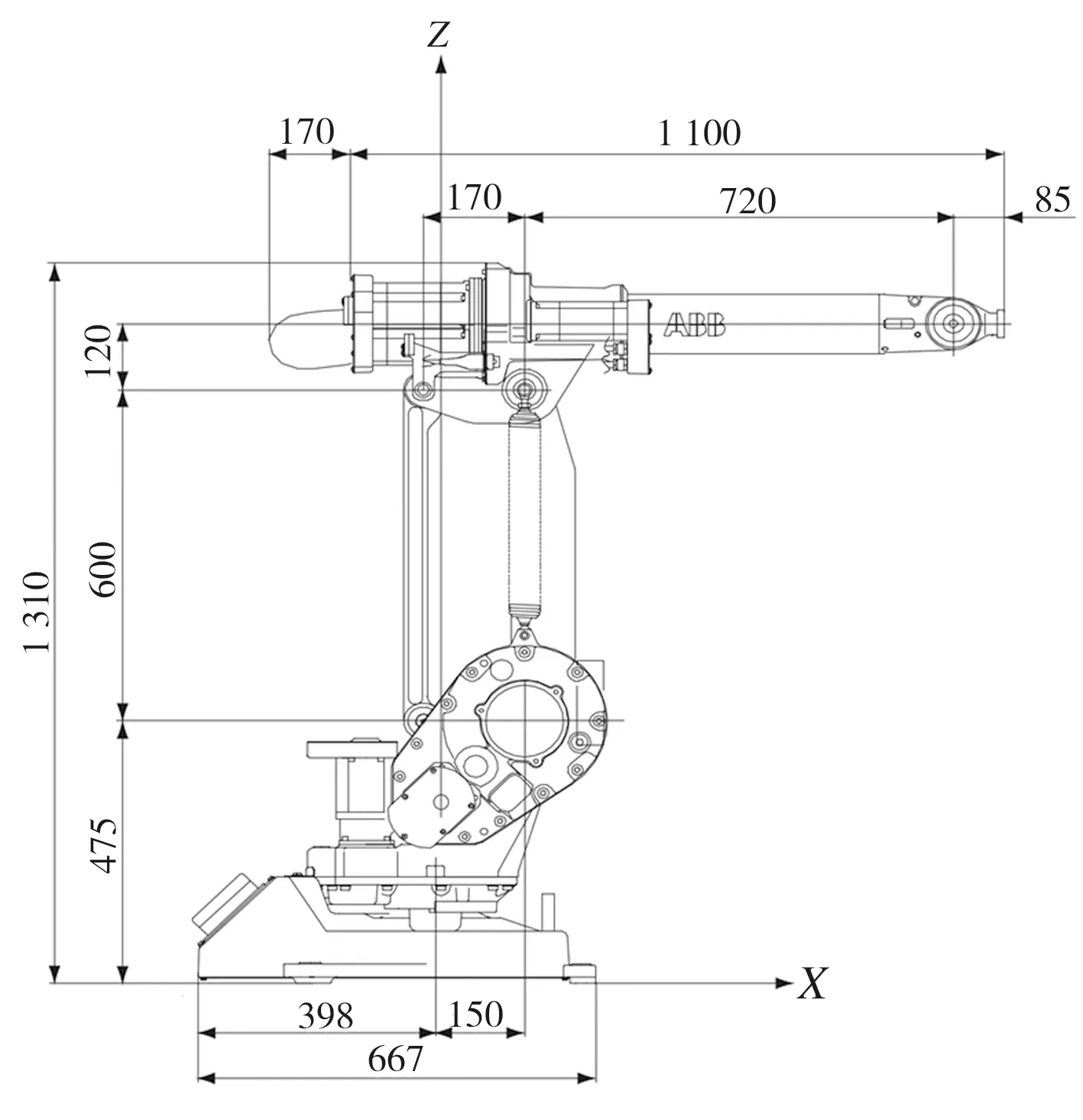
图3 IRB 1410机器人尺寸图(单位:mm)
2 焊接机器人运动学分析及仿真
2.1 焊接机器人正运动学分析及仿真
2.1.1 焊接机器人正运动学分析
焊接机器人正运动学分析目的是通过关节转角或关节移动参数来求解机器人的末端位姿[11]。将IRB 1410机器人的MDH参数代入式(1),求得相邻两杆坐标系之间的变换矩阵:
(2)
继而得到机器人末端坐标系相对于基坐标系的变换矩阵:
(3)
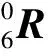
由于IRB 1410机器人结构参数已经确定,相邻两杆坐标系的变换矩阵只与对应的关节转角 相关,通过关节的空间参数即可求得机器人的末端位姿。
2.1.2 焊接机器人正运动学仿真验证
采用ABB集团的RobotStudio离线仿真软件构建机器人模型(如图5所示),通过虚拟示教器FlexPendant来调节机器人关节转角和末端位姿(如图6所示)。

图5 RobotStudio中的IRB 1410机器人模型
在相同的关节转角下,采用不同方式计算机器人末端位姿,通过比较可判断机器人正运动学求解的正确性。随机取10组关节转角数值(见表2),记录RobotStudio中机器人的末端位姿作为仿真值,计算所得的机器人末端位姿值作为理论值。在MATLAB中通过函数rotm2eul(T*rotz(180,′deg′),″ZYX″)将计算所得机器人末端姿态矩阵中的旋转矩阵转换为RobotStudio中机器人末端坐标系下的欧拉角,所得理论值与仿真值的位置和姿态误差绝对值如图7、图8所示。
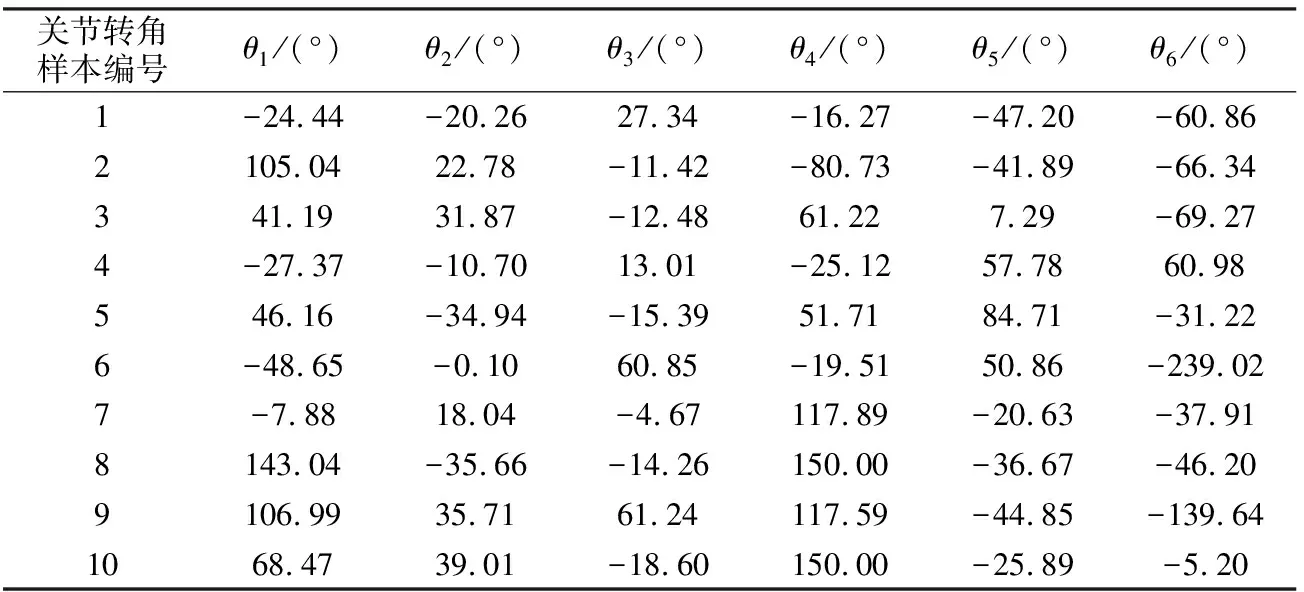
表2 RobotStudio中关节转角的随机取值
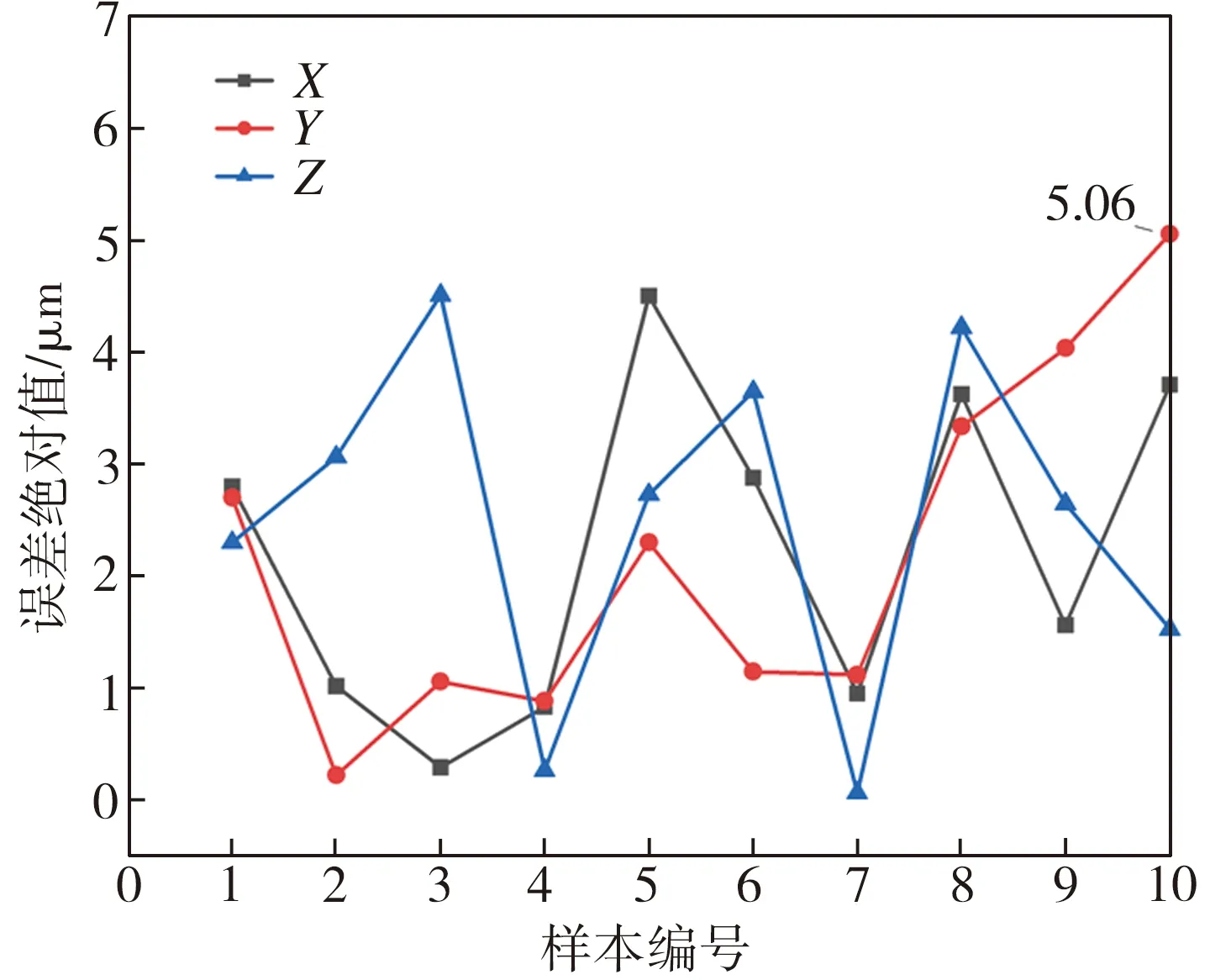
图7 正运动学分析的位置误差

图8 正运动学分析的姿态误差
由图7、图8可知,机器人位置与姿态的仿真值与理论值绝对误差的最大值分别为5.06 μm和0.00474°,位姿误差很小,说明所构建的正运动学模型是合理的。
2.2 焊接机器人逆运动学分析及仿真
2.2.1 焊接机器人逆运动学分析
焊接机器人逆运动学分析是通过机器人末端位姿求解出机器人的关节转角或关节移动参数,逆运动学解可分为解析解和数值解两类。在同一位姿下,机器人的逆运动往往对应着多组关节转角,求解时需要考虑求解速度和计算效率,解析解求解速度快、计算精度高[12],且IRB 1410焊接机器人的4、5、6关节轴线交于一点,符合Piper准则,可以得到机器人运动学问题的封闭解。
(1)求解θ1
(4)
(5)
分析矩阵方程(5)得到:
(6)
其中si和ci分别代表sinθi和cosθi,则得:
θ1(1)=atan2(py-d6r23,px-d6r13),
θ1(2)=atan2(d6r23-py,d6r13-px)
(7)
由式(7)易知θ1有2个可能解且两解相差π。
(2)求解θ3、θ2
(8)
分析矩阵方程(8)得到:
(9)
其中sij和cij分别代表sin(θi+θj)和cos(θi+θj)。
进一步有
(10)
由式(10)可得:
a3c3-d4s3=k
(11)
(12)

据式(12)求得θ3后,结合式(10)可得:
(13)
由θ1和θ3的一组值可以确定θ2的一个解,θ1和θ3有4种组合方式,可得到θ2的4个可能解。
(3)求解θ4、θ5、θ6
由式(6)、式(9)可得:
(14)
当s5≠0时,可求得:
(15)
针对大小相同符号相反的s5,θ4有2个相差π的可能解。确定θ4的值后,由式(6)、式(9)求得:
(16)
其中,当s4≠0且c4≠0时,s5(1)与s5(2)大小相等。
由矩阵方程(5)可得:
(17)
由式(17)可得:
θ6=atan2(r11s1c4-r12s1s4s5-
r21c1c4+r22c1s4s5,r11s1s4s5+
r12s1c4-r21c1s4s5-r22c1c4)
(18)
当s5=0(即c5=1)时,式(14)中分母为零,等式不成立,机器人发生腕部奇异。可通过式(17)求得:
θ4+θ6=atan2(r11s1-r21c1,r12s1-r22c1)
(19)
其中r11、r21、r12、r22已由机器人末端位置确定。
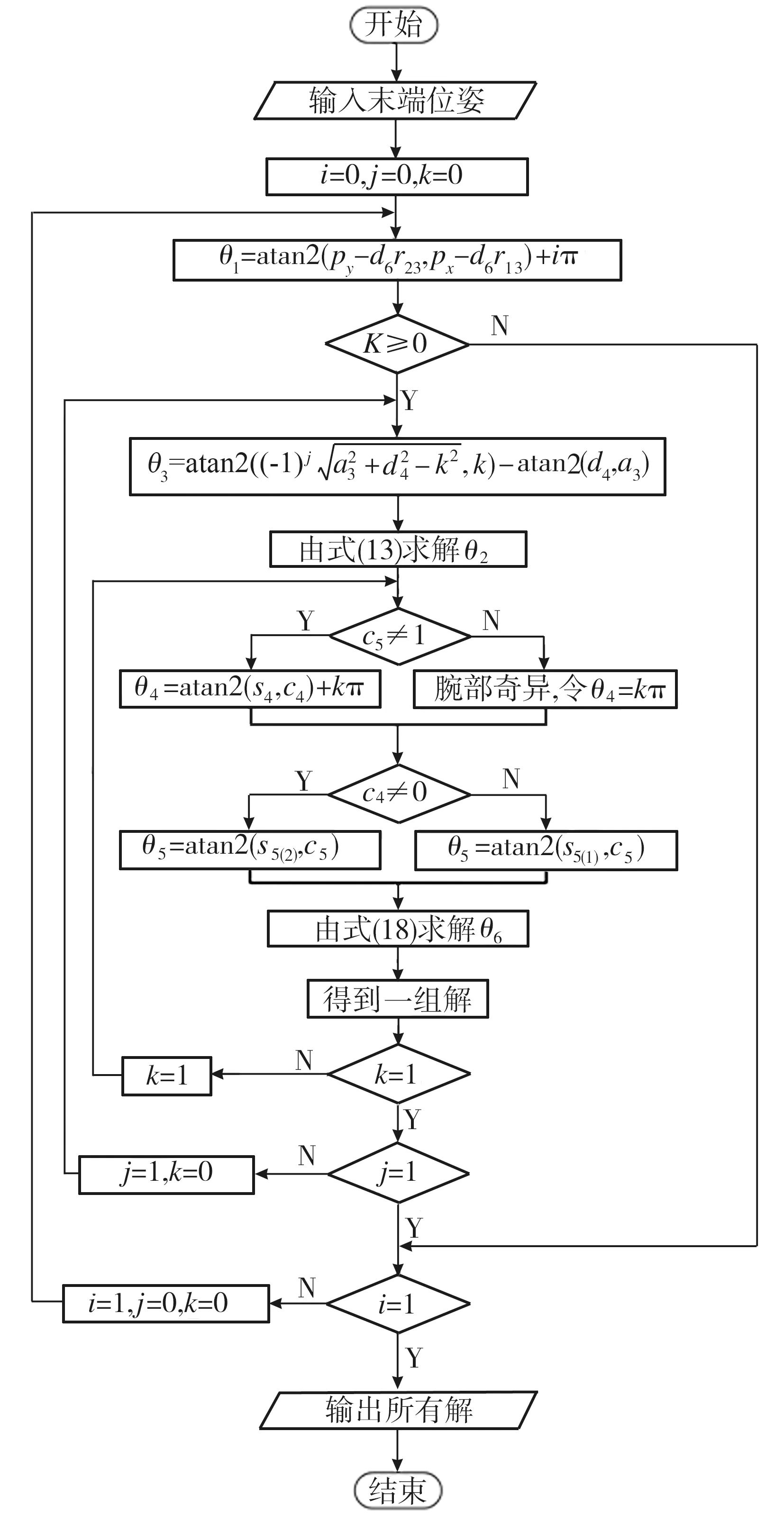
图9 逆运动学算法流程
2.2.2 焊接机器人逆运动学仿真验证
在机器人正运动学求解中,由一组随机关节转角可得到与之对应的唯一末端位姿,将所得末端位姿变换矩阵作为逆运动学模型仿真验证时的输入位姿矩阵,可求得此条件下机器人关节空间的所有解。通过正运动学分析求出多组关节转角各自对应的机器人末端姿态矩阵,与逆运动学输入姿态矩阵对比,来验证逆运动学算法的正确性。
使用Simulink搭建逆运动学验证模型,如图10所示。采用不同的初始种子设置随机信号,作为正运动输入关节转角的数值,采样时间为10 s,采样步长为0.05 s。图10中,Sub1模块用于阻断空解的传递;由于姿态变换矩阵含有16个元素,不易比较,故而通过设置Add和max_matrix_Sub模块求取姿态变换矩阵中元素差值的最大值。通过逆运动学求解得到每组解对应的姿态变换矩阵,取变换矩阵元素差值的最大值作为逆运动学算法检验指标,结果如图11所示。由图11可见,姿态变换矩阵元素误差值非常小,其数量级为10-12,表明本文提出的逆运动学算法是正确的。
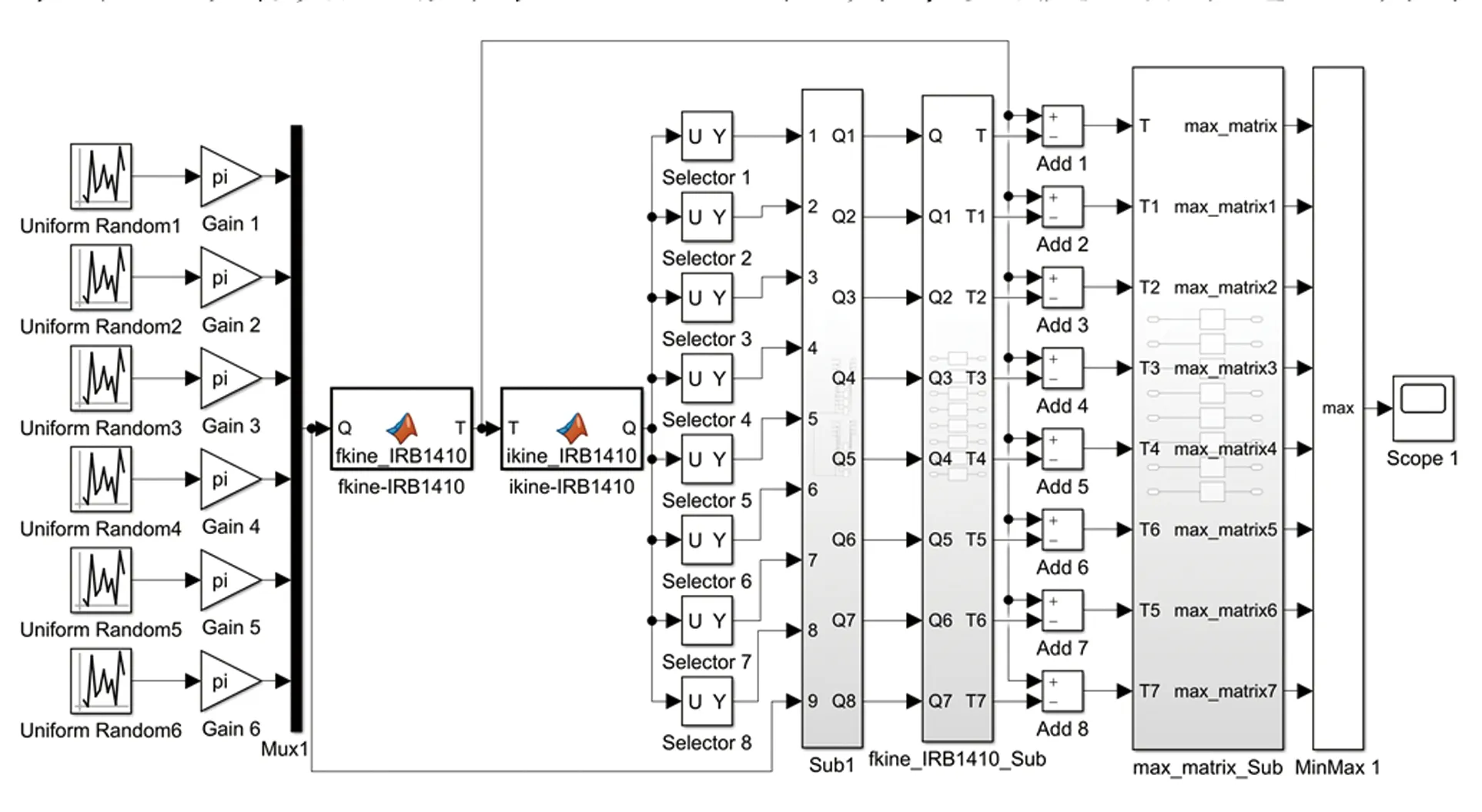
图10 Simulink逆运动学验证模型

图11 逆运动学求解误差
3 面向复杂空间路径的焊接轨迹规划
已知焊接机器人的运动学模型,可根据具体任务对焊接机器人进行轨迹规划,得到其运动过程中的位置、速度、加速度等相关参数。本文以管-管垂直相贯的马鞍形焊缝为对象进行焊接轨迹规划。焊接件模型如图12所示,Oob-XobYobZob为工件坐标系。

图12 焊接件模型
焊接机器人与工件的位置关系如图13所示。整个焊接任务分为3段:①焊接机器人由初始原点出发到达焊接起始点;②由焊接起始点沿马鞍形焊道开始焊接至焊接终止点;③由焊接终止点返回初始原点。在第二段任务过程中焊枪绕Zob轴作回转运动,由于马鞍形焊缝落差的存在,需要在回转的同时沿焊缝进行上下插补运动。焊接机器人位于初始位置时关节转角为[0° -30° 30° 0° 60° 0°]。

图13 机器人与工件的位置关系
实际焊接过程中,马鞍形焊缝通常需要多层多道焊[13],对于多层焊缝并不用多次反复规划,只需规划焊道在坡口截面的位置,然后在焊接过程中通过对焊枪偏移量的适当调整即可实现多层多道自动焊接[14],故本文只规划第一层焊接轨迹。对于马鞍形焊缝,当对应的副管尺寸和壁厚较小而主管尺寸和壁厚较大时,马鞍形焊缝落差较小,两面角和前后倾角对焊缝成形的影响基本可以忽略[13]。焊接过程中,焊枪XtoolOtoolZtool平面过竖管轴线,焊枪相对于焊缝的姿态如图14所示。马鞍形焊接轨迹如图15所示,箭头方向为焊枪Ztool轴所指方向。
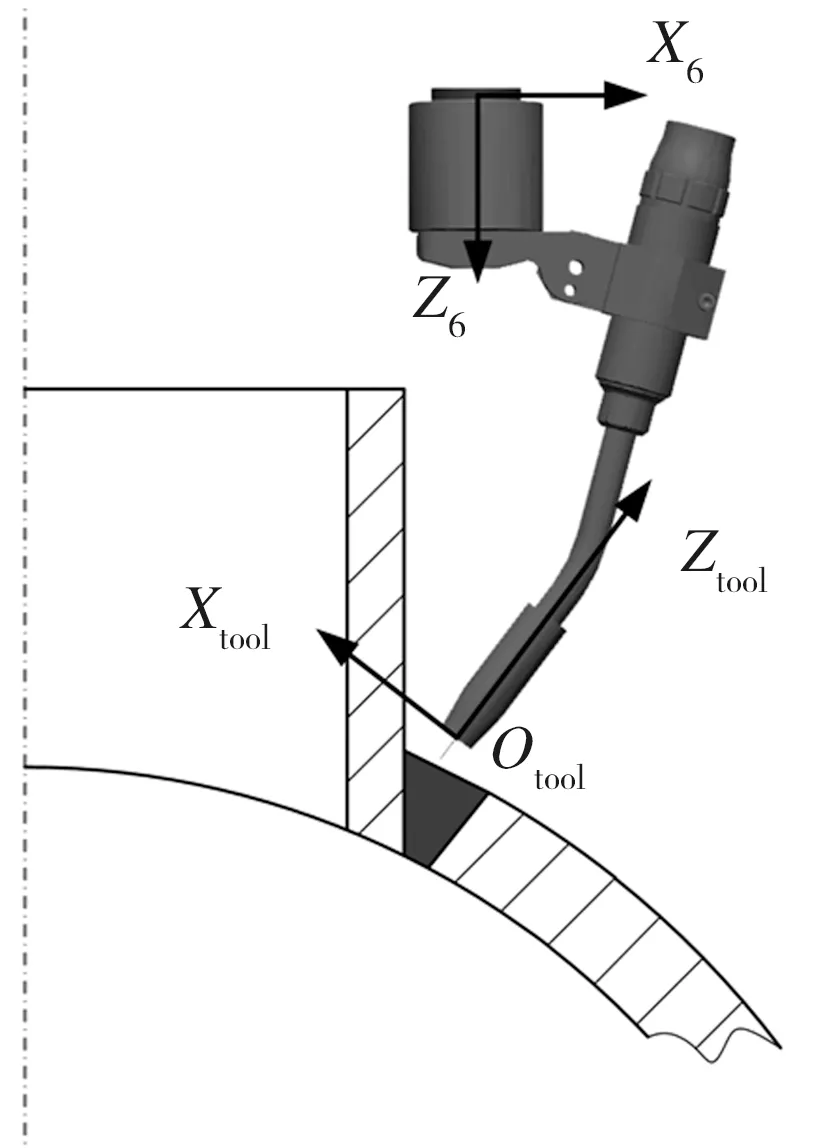
图14 坡口截面焊枪姿态图
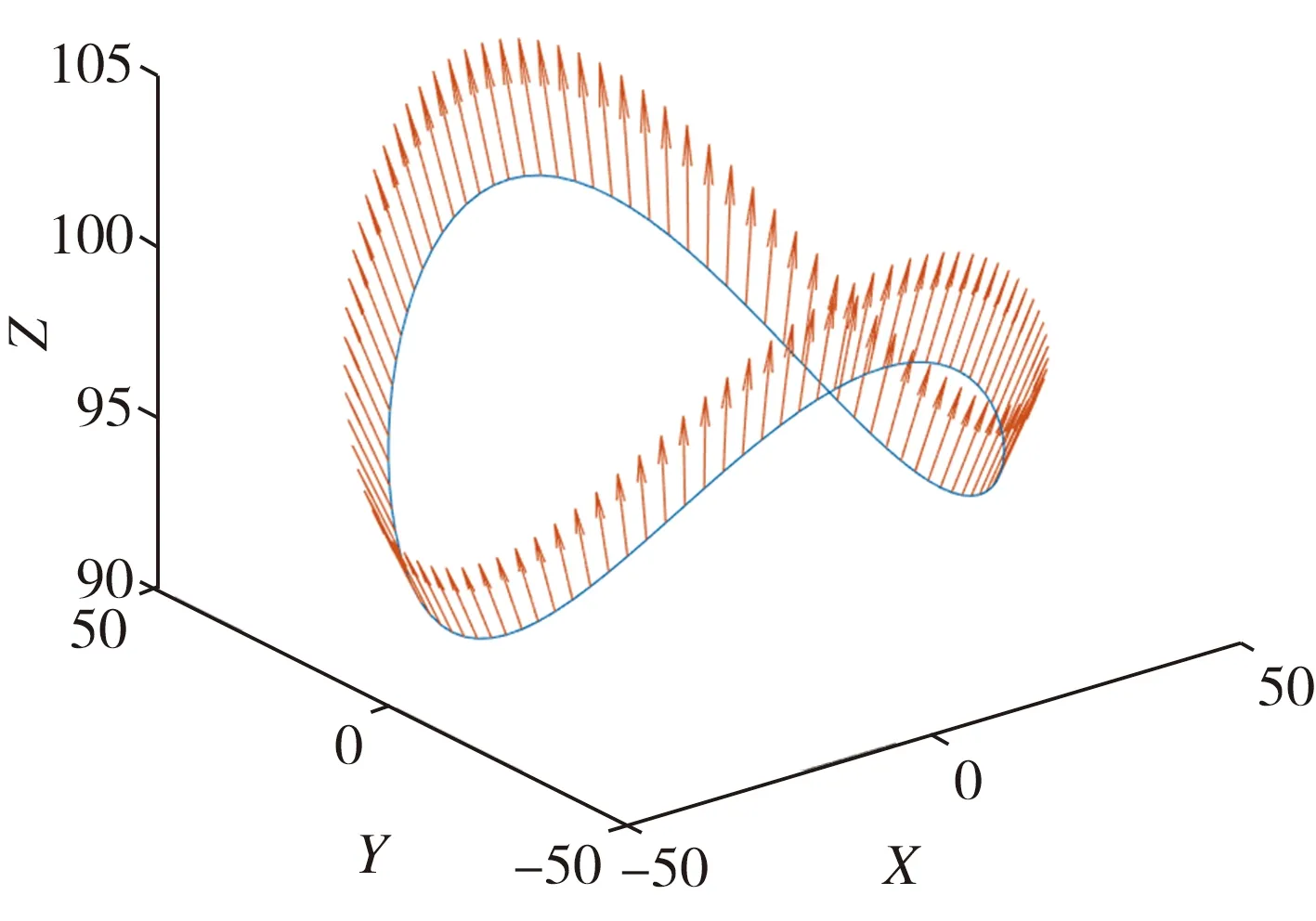
图15 马鞍形焊接轨迹
本文研究的马鞍形焊缝在工件坐标系上的位置解析式为:
(20)
在式(20)中,通过角度参数θ即可在Oob-XobYobZob坐标系上确定一个唯一的位置点,通过恒定的步进角度进行等角度插补,便可求出各个插补点的位置[15]。
(21)
式中:n为插补点的序号;Δθ=2π/N,其中N为插补点个数。

(22)

焊接过程中,焊枪沿马鞍形回转一周用时t=50 s。通过逆运动学模型可求出焊接过程中各关节角度、角速度和角加速度的变化(如图16所示)。
由图16可看出,IRB 1410机器人在对马鞍形焊缝的焊接过程中,各关节角度、角速度和角加速度的变化曲线较为连续平滑,没有突变的情况。然而,在焊枪做回转运动的开始和截止时刻,关节角速度和角加速度不全为零。为了使焊接机器人运动连贯,可通过五次多项式插值算法对焊枪由初始位置至焊接起始点以及由焊接终止点至焊接初始位置的轨迹进行规划,使其与马鞍形焊接轨迹相衔接[16]。
焊接机器人由初始位置经过5 s后到达焊接起始点,通过五次多项式插值得到这个过程中各关节的角度、角速度和角加速度的变化(如图17所示)。由图17可以看出,由初始位置至焊接起始点运动过程中,机器人关节运动参数曲线变化平滑,末端关节的角度、角速度和角加速度能与图16中焊接起始点处末端关节的运动状态衔接,使得机器人在整个焊接任务中的运行轨迹保持平稳连续。
4 结语
本文在对IRB 1410焊接机器人进行结构分析后,采用MDH法建立连杆坐标系,通过矩阵变换求得机器人末端相对于基坐标的位姿矩阵,构建了正运动学模型,并推导出IRB 1410机器人逆运动学的解析解,构建了逆运动学模型。同时,本文还设计了IRB 1410的逆运动学算法,并搭建Simulink仿真模型对逆运动学算法的正确性进行了验证。根据所建立的运动学模型,对管-管垂直相贯的马鞍形焊缝进行了等角度插补轨迹规划,并通过五次多项式插值将焊接机器人由初始位置至焊接起始点的轨迹与马鞍形焊接轨迹相衔接。本文构建的焊接机器人运动学模型较为合理,机器人焊接轨迹连续平稳,研究结论可为焊接机器人的运动学分析及焊接路径规划提供理论与实践依据。
