重载列车作用下新型预应力路基动应力响应规律研究
2023-10-13董俊利冷伍明张期树徐方聂如松
董俊利,冷伍明,2,张期树,3,徐方,2,聂如松,2
(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 中南大学 重载铁路工程结构教育部重点实验室,湖南 长沙,410075;3. 中南林业科技大学 土木工程学院,湖南 长沙,410004)
预应力路基是一种新型铁路路基结构形式,它既适用于新建线建设,也特别适合于既有线的加固与强化[1]。前期既有研究工作主要针对附加应力扩散规律及其分布特征研究、预应力路基边坡稳定性分析方法的构建、合理板间距的初步设计思路、静力性能数值仿真分析以及预应力损失理论研究等方面[2-6]。而对于列车荷载与水平预应力耦合作用下预应力路基的动力响应规律还暂未研究。
众所周知,现场测试、模型试验与数值仿真分析是研究铁路路基动力响应特性的主要手段[7-9]。现场试验可以最真实地反映列车作用下路基的工作状态,但因测试位置常限于路基外轮廓,故难以获得路基内部核心区域的响应特性。模型试验则以小比尺为主,因其相似判据难以一一满足,导致试验结果无法完全映射至实际工况。随着计算机的快速发展,数值仿真方法以成本低、可操作性强、分析工况可控、数据提取全面、模型尺寸可调等优点,成为解决各类工程问题的高效研究手段,并在铁路路基动力响应分析中得到了广泛应用。
近年来,已有大量铁路路基动力响应方面的有限元模型被提出。如:CHEN等[10-11]建立了无砟轨道路基的三维有限元模型,分析表明路基动应力峰值随列车运行速度的增大而增大。庄妍等[12]建立了桩承式路堤三维有限元模型,发现线路竖向速度与加速度从道床顶面到地基顶面均衰减了80%。XU 等[13]基于车辆-轨道耦合动力学理论[14],建立了国内重载铁路典型路基段三维动力有限元模型,指出列车相邻转向架引起的动力响应存在显著的叠加效应。商拥辉等[15]开展了列车-有砟轨道-基床-地基动力系统耦合三维有限元仿真分析,发现重载铁路列车运行时,动应力影响深度达3~4 m,超过基床设计厚度2.5 m。此外,轨道不平顺通过影响轮-轨接触关系而影响路基的动力响应[16-17]。KOUROUSSIS等[18]研究了轮-轨不平顺关系,并总结了轮-轨类型和轮-轨接触状态对振动响应的影响。
综上可知,目前关于铁路路基动力响应特性方面的研究已取得较为丰硕的研究成果,但其分析对象均为常规路基,而新型预应力路基在常规路基中引入了预应力加固结构,是一种全新的路基结构体系,其结构形式必然异于既有研究对象,故现有关于铁路路基动力响应方面的研究成果无法反映预应力路基动力响应规律。因此,目前亟待开展铁路预应力路基在动力性能方面的研究工作,合理探究列车动载、轨道不平顺以及水平预应力耦合作用对路基动力响应特性的影响。本文作者建立列车-轨道-路基(预应力路基和常规路基)三维动力有限元数值模型,并考虑轨道不平顺的影响,对比研究不同列车轴重下,常规路基与预应力路基基床层内动应力响应规律以及预应力路基中核心施力构件(预应力钢筋)的振动响应特性,系统揭示预应力路基结构的瞬态动力响应特性。
1 列车-轨道-路基-预应力加固结构三维动力有限元数值模型
1.1 重载列车模型
为反映前后节车厢相邻转向架的振动叠加效应,本文模型选取2节车厢。其中,车厢、转向架和轮轴设置为刚体。悬挂连接系统采用Cartesian形式的线性弹簧-阻尼单元。建立如图1 所示具有10个自由度的车辆模型。车体和转向架考虑沉浮、点头振动位移,而轮对仅考虑沉浮振动位移[19]。图1中:Mc为车体质量;Jc为车体点头惯量;Mt为构架质量;Jt为构架点头惯量;Mw为轮对质量;Kpz为一系悬挂刚度;Cpz为一系悬挂阻尼;Ksz为二系悬挂刚度;Csz为二系悬挂阻尼。
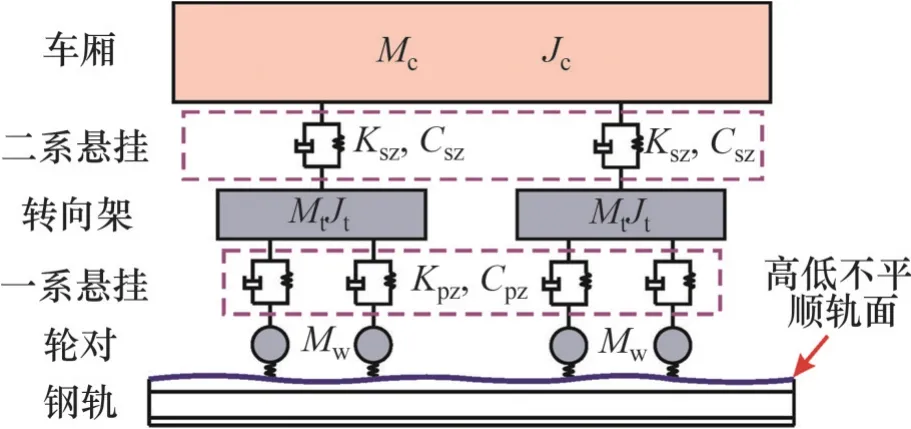
图1 二系悬挂系统力学连接关系Fig. 1 Mechanical connection relation with double suspension system
本文为对比分析大轴重列车作用下常规路基和预应力路基的瞬态动力响应差异,分别选取列车轴重25 t、30 t和35 t共3种工况,具体几何参数如表1所示,其中35 t轴重列车采用C96敞车模拟,敞车结构见图2;车辆结构计算参数如表2所示。

表1 重载列车几何参数Table 1 Geometric parameters of heavy-haul train
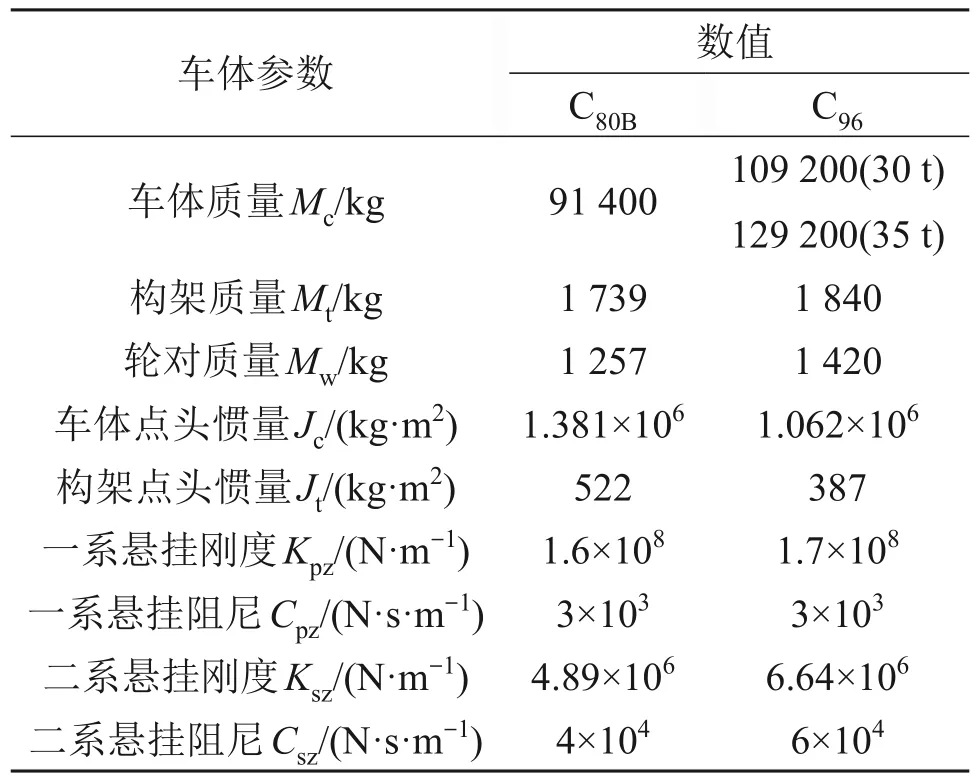
表2 车辆结构计算参数Table 2 Calculation parameters of vehicle structure

图2 列车结构参数Fig. 2 Geometrical specification of train
1.2 轨道-路基-预应力加固结构模型
常规轨道-路基系统主要结构为钢轨、垫板、扣件、轨枕、道砟、路基和地基;而预应力路基则增添了预应力加固结构(即预应力钢筋和侧压力板),如图3 所示。数值模型中,钢轨与轨枕间采用线性弹簧-阻尼连接器模拟二者间的传力模式以替代扣件和垫板的作用,其竖向刚度取100 MN/m,竖向阻尼系数取6×104N·s/m,弹簧-阻尼单元的纵向间距为0.60 m,如图4所示。侧压力板、轨枕及下部结构层均采用C3D8R 单元类型,钢筋选用二力杆T3D2单元。路基体3个结构层(基床表层、基床底层和路基本体)和地基层均采用Mohr-Coulomb本构模型,其余构件如轨枕、预应力钢筋和侧压力板则考虑成线弹性体。本文重点分析2种路基结构在不同轴重列车运行下路基的动应力响应规律,未考虑道砟颗粒如何准确传递列车荷载作用,因此,道砟层也采用线弹性模型。轨枕-路基-地基耦合模型的本构参数取值参照朔黄重载铁路各结构层的相关试验结果[20],具体如表3所示。

表3 轨道-路基-预应力构件的材料参数Table 3 Material properties of track subgrade and prestressed members

图3 预应力路基结构示意图Fig. 3 Schematic diagram of prestressed subgrade structure

图4 钢轨-轨枕间的连接方式Fig. 4 Connection mode between rail and sleeper
为使预应力钢筋达到目标张拉值,不因满足变形协调而出现预拉力损失,本文采用Bolt Load法[21]模拟钢筋预应力的张拉和锁定,如图5 所示。此外,钢筋端部与侧压力板间的连接采用耦合约束替代锚固元件作用,力学模式为平动自由度(U1、U2、U3)受约束,而转动自由(UR1、UR2、UR3),较贴合二者实际工作状态。因侧压力板在正常工作中很难向上滑动,即侧压力板与路基边坡应保持为紧密接触状态,因此,板-土接触关系在法向设置为“硬接触”,而切向设置为“粗糙接触”,以确保侧压力板稳定“趴”于路基坡面。

图5 侧压力板与预应力钢筋Fig. 5 Lateral pressure plates and prestressed steel bars
轨道-路基结构几何尺寸依据重载铁路设计规范中的标准单线断面尺寸建立,具体几何尺寸见表4。其中,侧压力板底面边长设为1.2 m,预应力钢筋直径为25 mm,规格为HPB300热轧光圆钢筋,对应公称截面积为4.098×10-4m2。考虑到预应力钢筋对坡面侧压力板的对拉约束作用,同时也为更好地体现预应力结构的加固作用,本文将常规路基坡率由1:1.5调整为1:1.0。

表4 轨道-路基模型几何参数Table 4 Geometrical parameters of track subgrade model
1.3 轮-轨接触模型
为避免模型网格入侵导致计算不收敛,需合理设置轮-轨接触对中的主从面关系。在此,车轮设为刚体,钢轨为弹性体,轮-轨接触采用面-面接触关系,车轮表面为主面,钢轨表面为从面,具体关系如图6所示。
求解列车与轨道间的动力学运动方程需建立有效的轮-轨力学接触关系。常用的轮-轨接触关系采用非线性Hertz 接触理论和罚函数摩擦(Penalty)模型,分别考虑法向和切向接触行为,其计算精度高且易收敛。因此,本文切向接触关系中的切向摩擦因数取0.2。在轨道平顺条件下,法向相互作用由Hertz非线性弹性接触理论确定[14]:
式中:P(t)表示某时刻t对应的轮轨法向作用力;δz(t)表示某时刻t对应的轮轨竖向相对压缩值;G表示轮轨接触常数。
轮轨接触常数G在针对磨损型踏面车轮时,按式(2)计算取值。
式中:R表示车轮半径。
对于不平顺轨道情形,本文以单节车厢4个轮对为研究对象,则某时刻t对应的轮轨法向接触力Pj(t) (j=1,2,3,4)可按式(3)进行计算。
式中:Zwj(t)、Zr(xwj,t)和Z0(t)分别表示某时间t对应第j个轮对下的沉浮位移、钢轨位移和轨面高低不平顺位移。则据此可得单节车厢4个轮对组与钢轨间的法向接触力。
采用Soft-Contact中的Tabular模式来描述上述轮轨法向接触行为,而定义该行为时需预设接触面的过盈量与接触力的关系,当轮轨脱离产生间隙时,接触压力为0,如图7所示。

图7 轮-轨法向接触模式示意图Fig. 7 Schematic diagram of wheel-rail normal contact mode
1.4 轨道不平顺
轨道不平顺会对行车安全及平稳舒适性构成不利影响。依据激扰方位的不同,轨道不平顺可分为高低不平顺、水平不平顺、轨距不平顺和轨向不平顺。其中,高低、水平不平顺对系统的垂向激扰程度最大,而水平不平顺是由高低不平顺派生而来[22]。因此,本文仅考虑高低不平顺。
徐磊等[23]基于朔黄重载铁路的轨道不平顺检测数据,获得了表征朔黄重载铁路线路不平顺特征的轨道谱函数。本文结合研究重点,采用其高低不平顺的轨道谱建议表达式:
式中:S(f)为轨道不平顺功率谱;f为空间频率;a、b、c和d为谱密度函数的拟合特征参数,各参数具体数值如表5所示。

表5 朔黄重载铁路轨道高低不平顺统计谱特征参数Table 5 Characteristic parameters of vertical irregularity track spectrum of Shenchi—Huanghua heavy haul railway
轨道不平顺常用的模拟方法为逆傅里叶变换法、三角级数法、二次滤波法和白噪声滤波法。逆傅里叶变换可比较真实地再现线路的空间不平顺状态。故本文采用快速傅里叶逆变换(IFFT)方法将不平顺轨道功率谱转化为沿线路纵向的空间分布不平顺幅值。
将上述朔黄重载铁路轨道高低不平顺功率谱利用Matlab 软件转化成沿线路纵向连续随机分布的不平顺幅值,并取空间波长0.5~100.0 m,车辆运行速度v=80 km/h,即可得到左、右高低不平顺样本幅值沿路基线路纵向的空间分布图。轨道高低不平顺建模过程如图8所示。

图8 轨道高低不平顺建模过程Fig. 8 Modeling process of track vertical irregularity
1.5 材料阻尼参数
阻尼决定振动能量衰减的快慢,数值模型中除轨枕、侧压力板和预应力钢筋外,将道砟层、路基结构层和地基均考虑为黏弹性体,采用Rayleigh阻尼模型,其阻尼矩阵C是由质量矩阵M和刚度矩阵K线性组合而成[24]:
式中:αR为质量比例阻尼系数;βR为刚度比例阻尼系数;D为阻尼比;ω1为模型基频;ω2为对路基系统动力响应有显著影响的高阶振型频率。
采用振型叠加法对路基模型进行模态分析,以获得路基结构的振型和固有频率[25]。计算确定该路基模型中的两个目标圆频率分别为ω1=9.815 rad/s 和ω2=15.152 rad/s。本文模型中材料的阻尼比D取值见文献[19],将ω1、ω2和D分别代入式(6)和式(7)可获得各结构层的阻尼系数αR和βR。表6所示为各结构层的Rayleigh阻尼参数。对于模型端部动力边界的处理,由于距离列车动荷载较远,可采用黏弹性人工高阻尼吸能边界,将阻尼比D设置为1.0,以模拟无限远地基吸收动力波并减少边界反射波的影响[19]。

表6 模型材料Rayleigh阻尼计算参数Table 6 Model material Rayleigh damping calculation parameters
路基在列车荷载作用下的应力分量中竖向应力分量最大,且基床层动力响应程度最高[25]。因此,本文重点分析两种路基结构钢轨正下方处的竖向动应力峰值,以此对比二者在动力瞬态响应方面的差异。
1.6 路基模型与分析过程
分别建立常规路基和预应力路基三维动力有限元模型,如图9所示。图中,X轴代表线路横断面方向,Y轴代表竖直方向,Z轴代表线路纵向。由于有限元模型尺寸对计算量和计算精度均有一定影响,故考虑两个路基模型的纵向长为96 m,横向(X向)边界距路基坡脚32.25 m。路基模型深度的设置需结合路基动力响应的衰减情况考虑,重载铁路路基面以下2.5 m深度处动应力衰减量可达60%[13],则文中模型中地基深度设为10 m,模型底部距路基面的距离达到18 m,满足计算精度要求。常规路基模型节点数为685 699个,单元数为567 078 个,网格最大尺寸为11.7 m,最小尺寸为0.013 m;预应力路基模型节点数为719 413个,单元数为590 514 个,网格最大尺寸为11.7 m,最小尺寸为0.013 m。
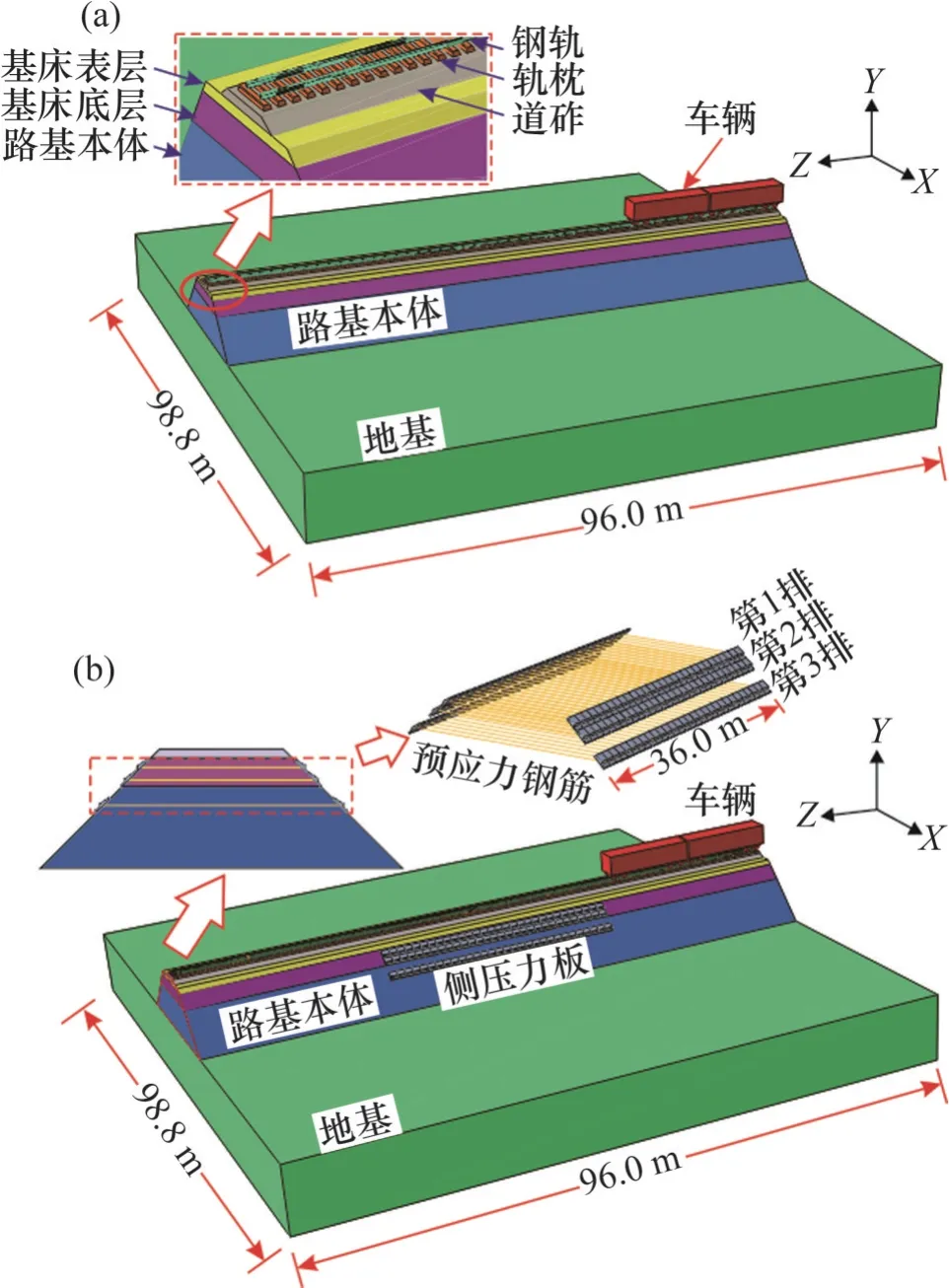
图9 车辆-轨道-路基(预应力路基)三维有限元模型Fig. 9 3D finite element model of train-track-subgrade(prestressed subgrade) system
基床层受列车动荷载影响最为显著,而其围压水平很低,属于病害重点源区。预应力路基具体加固方案为从基床底层底面向上连续布置两排预应力加固结构(第1、2排),另外在路基本体段布置第3排加固结构,为提高预应力在路基内的扩散均匀性,采用1.0倍板宽作为第2、3排加固结构间的上下净间距(见图10)。冷伍明等[5,26]的研究表明,当侧压力板布置在距离坡面路肩小于2.0倍板宽的净距离时,极易引起路肩段土体发生“上拱剪切破坏”,故第1 排钢筋预拉力初始值为其余各排的50%,即第1~3排加固结构的等效预压面荷载分别为50、100、100 kPa。在该种加固模式下,依据预应力路基附加围压扩散理论[5],可计算出双侧预应力加固结构在基床表层对应钢轨正下方位置所产生的附加围压约为30 kPa,由此提高基床层围压水平与侧限作用。

图10 预应力加固结构布置方案Fig. 10 Layout scheme of prestressed reinforced structure
在预应力路基中,每横排沿线路纵向连续布置30 块侧压力板。针对2 种路基结构中间段(36 m长度范围)内的动力响应开展对比分析。模型边界条件设置为:地基底面采用全固定约束,路基纵向两端采用法向对称约束,模型横向两端约束X向位移。表7所示为本文的具体仿真工况。
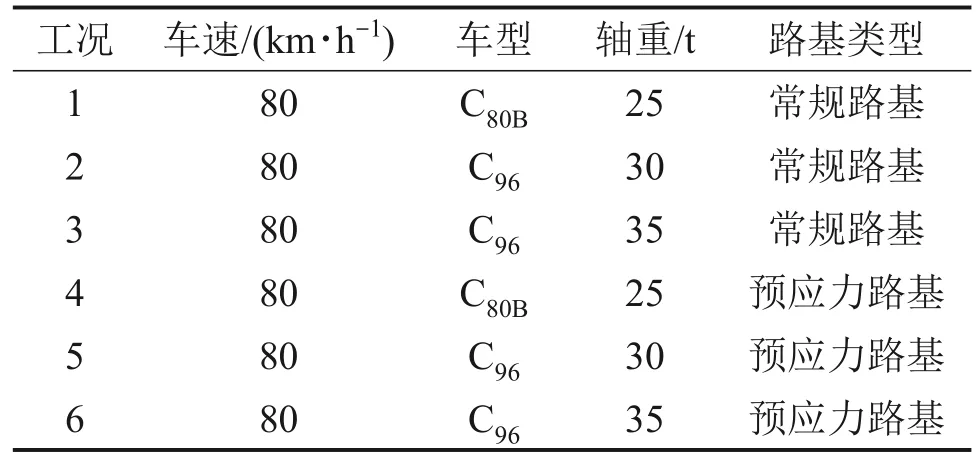
表7 仿真计算工况Table 7 Numerical simulation cases
对2种路基结构开展动力仿真分析时,首先都采用Geostatic 分布步模拟产生初始自重应力场,即施加地基、路基和轨道部分的自重荷载,它可自动清除位移场。对于后续分析步,常规路基仅添加列车移动荷载作用即可;而对于预应力路基,在完成自重应力场分析后,计算预应力加固结构的自重作用,再张拉钢筋至目标预应力,由此形成预应力路基,最后计算移动列车荷载。
2 模型验证
表8所示为文献中有关现场试验[27-30]、模型试验[31]及数值模拟[13,15,32]的结果与本文常规路基数值模拟结果的对比。由表8可知:本文模型动应力峰值结果与既有文献结果位于同一数量级且峰值较为接近,在数值上具有较高的可信度,基本验证了本文数值模拟结果的正确性。

表8 重载铁路路基面动应力峰值统计Table 8 Peak value statistics of dynamic stress on subgrade surface of heavy-haul railway
3 基床层动应力峰值统计分析与正态性检验
3.1 路基面动应力时程特征分析
未经特别指出,文中动应力均指竖直方向的动应力。以线路纵向横断面Z=48 m(沿线路纵向中间截面)为研究对象,提取两种路基结构在不同轴重列车运行条件下,左、右钢轨正下方路基面P1和P2(见图11)的动应力时程曲线,如图12 所示。由图12 可知:两种路基结构下的路基面动应力受列车轴重影响显著,轴重越大,动应力水平越高,且左、右轨高低不平顺使钢轨下路基面动应力也产生了差异。同时,当前后节车厢两个相邻转向架通过时,其动应力水平相对较高,易达到峰值水平,这是两个相邻转向架4个轮对共同作用产生的动力叠加效果。

图11 路基动应力峰值分析位置Fig. 11 Analysis position of dynamic stress peak value of subgrade
对于断面Z=48 m处,在列车轴重为25、30和35 t作用下,常规路基左轨下方路基面动应力峰值分别为67.10、85.21和94.27 kPa,右轨下方路基面动应力峰值分别为67.32、85.38和97.98 kPa;而预应力路基左轨下方路基面动应力峰值在3 种轴重列车作用下分别为66.18、84.11和92.99 kPa,右轨下方路基面动应力峰值分别为65.73、83.47 和95.75 kPa。虽然两种路基结构间的动应力峰值差异较小,但在同一断面处,预应力路基动应力峰值普遍略低于常规路基动应力峰值,且在35 t轴重列车作用下,动应力峰值间的最大差值为2.23 kPa。
图13所示为两种路基结构在不同运行时间下,路基面动应力等值线分布云图(轴重30 t)。由图13可知:左、右轨高低不平顺幅值沿线路纵向存在相对高差,这导致路基面动应力在沿线路中线出现非对称分布特征,且差异化明显。在同一转向架所控制的2个轮载作用下,路基面动应力云图大致呈矩形分布,而2节车厢对应4个转向架在不同时刻下,路基面上的动应力分布表现为动态随机响应,即每个矩形内动应力的分布形态各不相同,且每个矩形内的最大值也存在差别,这与列车运行过程中受轨面不平顺所引起的垂向点头、沉浮运动密切相关,使得路基面动应力峰值的随机分布特点显著。此外,根据应力等值图例可知,2种路基结构在相同时刻下,路基面动应力峰值差异不太显著。具体来说,在t=1.0 s 时,预应力路基动应力峰值略大于常规路基动应力峰值;而在t=2.0 s 时,则是常规路基动应力峰值略高于预应力路基动应力峰值。

图13 两种路基结构在不同时刻路基面动应力云图(轴重为30 t)Fig. 13 Dynamic stress contours of subgrade surface of two subgrade structures at different times (axle load of 30 t)
沿线路纵向逐个提取轨下路基面网格单元的动应力峰值,经数据整理可获得其分布曲线,如图14所示。由图14可知:受轨道高低不平顺的影响,轨下路基面动应力峰值沿线路纵向在一定范围内呈波动分布,具有一定随机性。
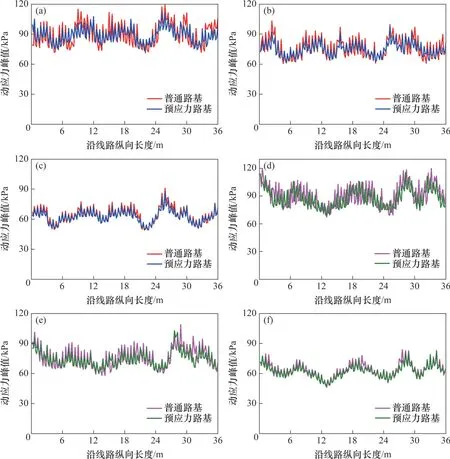
图14 路基面动应力峰值沿线路纵向分布曲线Fig. 14 Distributions curves of peak dynamic stresses on subgrade surface along track
由图14可知:2种路基结构下的动应力峰值随机离散分布程度均随列车轴重的增大而增大;在同一轴重下,预应力路基动应力峰值的整体离散程度相对偏低。以左轨下方路基面为例,当列车轴重为35 t 时,常规路基动应力峰值变动区间为[71.4,119.3] kPa,而预应力路基动应力峰值变化范围为[73.3,111.0] kPa;当列车轴重为30 t时,常规路基动应力峰值波动区间为[60.7,103.3] kPa,预应力路基变化范围为[61.7,97.7] kPa;当列车轴重为25 t时,常规路基和预应力路基下的动应力峰值变动区间分别为[49.4,91.2] kPa 和[49.5,88.5] kPa。综上可知,预应力加固结构在控制路基面动应力离散程度方面具有一定的积极作用,且轴重越大,控制优势越明显。
3.2 基床层内不同深度动应力峰值统计分析
在基床层左、右轨正下方沿垂向提取5个深度处的动应力峰值进行分析(见图11),分别对应路基面以下深度z为0、0.50、1.12、1.76 和2.40 m。图15所示为2种路基结构在不同列车轴重作用下,钢轨下方基床层不同深度处的动应力峰值统计均值。从图5 可以看出:由于预应力加固结构的强化作用,预应力路基的动应力峰值统计均值在不同深度均略低于常规路基的动应力峰值,而2种路基结构在3种不同轴重的列车作用下,基床层内动应力峰值均值沿深度衰减规律基本一致,近似呈负指数衰减。可采用动应力衰减系数η来描述动应力峰值在2种路基结构基床层内的衰减规律。通过对动应力峰值均值与深度进行负指数公式拟合,可获得二者间的具体关系表达式,如图16 所示,决定系数R2=0.99。可见预应力路基基床层内动应力衰减速率略低于常规路基动应力衰减速率。同时,本文数值仿真计算获得的路基动应力平均水平随基床深度的衰减曲线与文献[31]中室内足尺模型试验的实测曲线较为接近,由此也进一步论证了三维动力有限元仿真模型的可靠性。

图15 基床层动应力峰值统计均值Fig. 15 Statistical mean value of dynamic stress peak value in subgrade bed layer
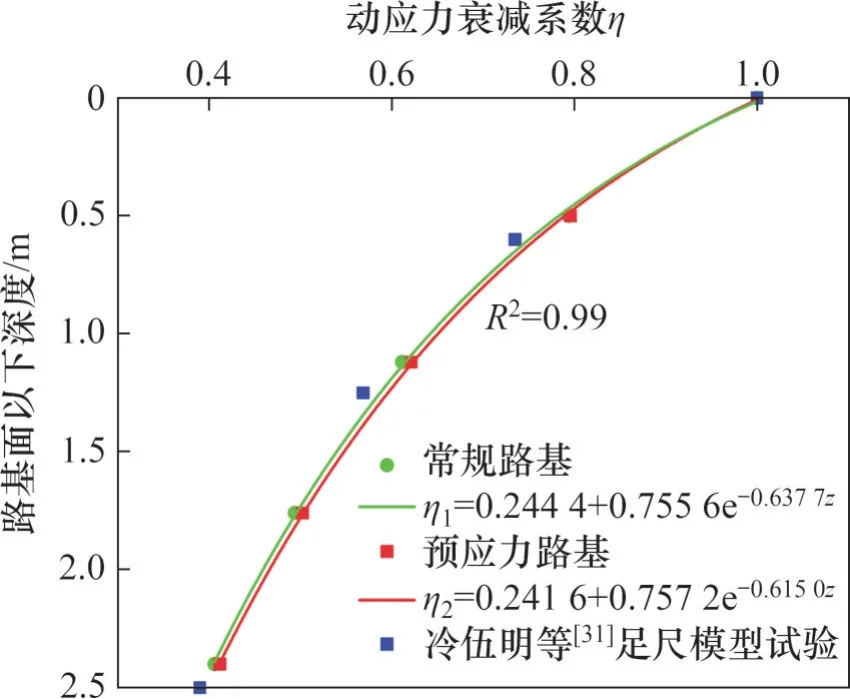
图16 动应力衰减系数沿基床层深度变化的关系曲线Fig. 16 Relation curves of dynamic stress attenuation coefficient along the depth in subgrade bed layer
由于轨道沿线路纵向存在高低不平顺,使路基动应力沿线分布呈显著的随机波动性。对此,采用概率统计学中的“变异系数”对2种路基结构动应力峰值数据的离散性进行对比分析。图17 所示为左、右轨下动应力峰值变异系数随基床层深度变化的统计结果。由图17可知:列车轴重越大,动应力峰值变异水平越高,即动应力波动离散程度越大,表明列车轴重对路基动应力存在变异放大效应,这进一步提升了对线路基础在抗动载方面的性能要求。此外,基床层动应力变异系数同样随深度逐渐衰减,且衰减速率由快及缓,与动应力均值随深度变化规律类似。由于预应力结构的强化作用,基床内的动应力峰值变异性得到了改善,且列车轴重越大,越能体现出预应力加固结构在控制路基动应力离散程度方面的优势。在列车轴重为35 t时,常规路基右轨下方基床内的动应力峰值变异系数范围为5.33%~14.12%,而预应力路基内的变异系数范围为4.95%~12.5%。因此,可认为预应力加固结构对维持路基动应力稳定存在有利作用,可在一定程度上抑制轨道高低不平顺给路基体带来的动力放大效应。
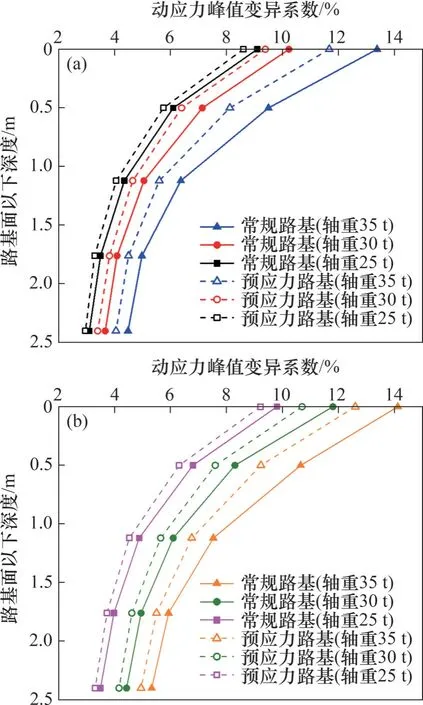
图17 动应力变异系数沿基床层深度变化的统计规律Fig. 17 Statistical law of variation coefficient of dynamic stress along the depth in subgrade bed layer
3.3 基床层动应力峰值正态性检验
文献[33]指出,轮对荷载的分布形式较符合正态分布,而轮载可通过扣件由钢轨传递至轨道结构最终扩散至路基内。对此,可采用柯尔莫哥洛夫-斯米洛夫(K-S)检验法对轨下基床层内的动应力峰值开展正态性检验,具体过程如下。
1) 若有限元仿真计算所得的动应力峰值样本(X1,X2,…,Xn)假定来自于总体样本X,则可求出其较优估计的经验分布函数Fn(σ),而Fn(σ)为理论分布函数,假设基床层内动应力峰值均符合正态分布形式,据此可提出2个相对立的假设,即
H0:动应力峰值样本来自的总体服从正态分布,Fn(x)=F0(x);
H1:动应力峰值样本来自的总体不服从正态分布,Fn(x)≠F0(x)。
2) 取K-S检验统计量:
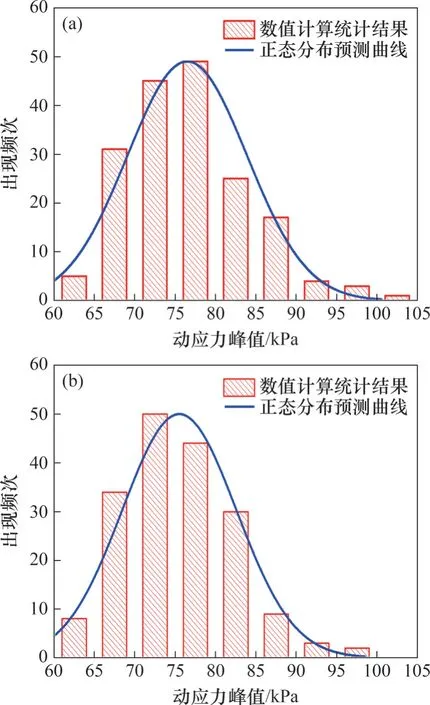
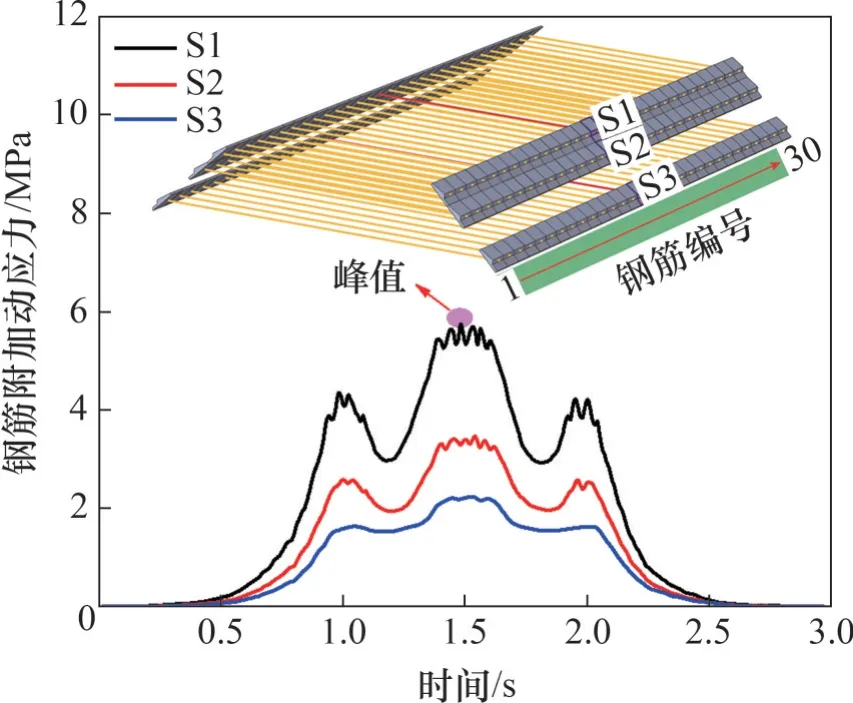
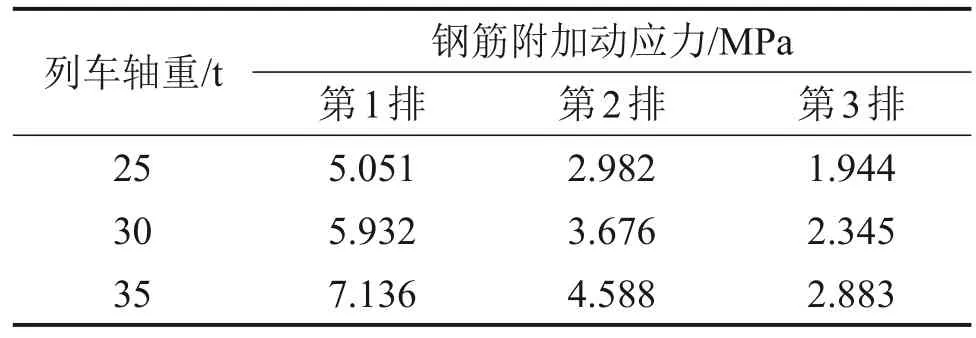
式(8)表示样本所服从的总体分布与理论分布间的最大差值。显然,当2个分布比较接近时,Dn就较小,可认为假设H0成立;反之,认为该假设不成立。具体可采用一个显著性水平α下对应的临界值Dn,α进行判别,当Dn 3) 求取待验证分布列的经验累积分布函数Fn(σi)为 4) 判断沿线路纵向分布的动应力峰值是否服从以下理论正态分布: 式中:为动应力样本均值;S*为标准差。 根据上述检验方法可计算出Dn,本文选取显著性水平α=0.01,查K-S 检验的临界值表[34]可知Dn,α=1.63/(n)0.5,经计算Dn,α=0.121 5。 表9所示为3种列车轴重作用下,左、右轨下方基床内5个不同深度处的Dn。由表9可知:每个深度位置处的统计值Dn均小于临界值Dn,α,表明受轨道不平顺的影响,基床内动应力峰值沿线路纵向均服从正态分布规律。图18 所示为30 t 轴重列车作用下,2种路基结构在左轨下方路基面的动应力峰值沿线路纵向的统计结果及其正态分布预测曲线。可见常规路基的动应力分布域更大,数据相对离散。 表9 基床层动应力峰值正态分布检验统计表Table 9 Statistical table of normality test of peak dynamic stresses in subgrade bed layer 图18 左轨下方路基面动应力频数直方图与预测分布曲线对比(轴重为30 t)Fig. 18 Comparison between frequency histogram of dynamic stress on subgrade surface under left rail and predicted distribution curve (axle load of 30 t) 作为预应力结构中的核心施力构件,预应力钢筋在列车动荷载作用下的内力变化情况可在一定程度上反映出加固结构的整体振动响应特性。对此,着重分析钢筋附加应力的变化情况。 图19 所示为30 t 轴重列车作用下,各横排第15 根预应力钢筋(S1、S2 和S3)的附加动应力时程曲线。由图19 可知:S1 动应力响应程度最高,当转向架通过时,其动应力时程曲线振荡响应相对最大,表明此时钢筋处于受力剧烈变化阶段,且在前后节车厢相邻转向架通过时同样出现了附加动应力峰值;而S2和S3的附加动应力响应程度沿坡面向下逐渐衰减。预应力钢筋S1至S3的动应力时程曲线形态由“三峰式”逐渐过渡为“单峰式”,这是由于路基体存在一定的阻尼耗能作用,使得坡面振动响应从路肩往坡脚逐渐衰减弱化。钢筋附加动应力响应水平由大到小顺序为S1、S2、S3。 图19 预应力钢筋附加动应力时程曲线(轴重为30 t)Fig. 19 Additional dynamic stress time history curves of prestressed steel bars (axle load of 30 t) 沿线路纵向提取路基内各横排预应力钢筋的附加动应力峰值,其分布曲线如图20 所示。从图20 可以看出:列车轴重越大,钢筋附加动应力峰值水平越高。每横排端部预应力钢筋的附加动应力峰值较大,这是由于加固结构端部处于常规路基段与预应力路基段的交界过渡区,该位置加固效果在整个预应力路基段内最弱,当列车经过此端部过渡区时,列车动载对该突变区产生相对较大的冲击效应,增大了钢筋动应力响应水平。此外,第1排预应力钢筋在不同轴重列车作用下所引起的附加动应力差异明显,且各分布曲线沿线路纵向波动幅度相对较大,第2排钢筋在不同轴重的列车作用下对应的分布曲线间差异水平有所下降,而第3排钢筋间的分布曲线差异性最小,且曲线变化相对平稳,这表明动荷载经基床层快速衰减后,到达路基本体上的坡面振动响应已较低且处于相对稳定状态。 图20 预应力钢筋附加动应力峰值沿线路纵向分布曲线Fig. 20 Longitudinal distribution curves of additional dynamic stress peak of prestressed steel bars along track 表10 所示为同轴重的列车作用下,各排钢筋附加动应力峰值沿线路纵向分布的平均值。由表10可知:由于第1排预应力加固结构布置在基床层中部坡面,其动应力峰值水平相对最高,但与钢筋静态目标张拉应力相比,其振动响应程度很低。如在35 t轴重列车作用下,第1排钢筋附加动应力均值仅为7.136 MPa,而目标张拉应力为146.7 MPa,其变化率低于5%,表明预应力钢筋在列车荷载经过时,所受振动影响程度很低,响应偏于缓和。此外,尽管第1、2 排加固结构是沿基床底层坡面紧密布置,但其间的附加动应力均值存在较大差别,表明振动作用在基床层衰减较快;而第3排加固结构因布置在路基本体,钢筋振动响应水平最低,其均值水平仅为第1 排钢筋的26.4%,可见其附加动应力已大幅衰减,表明在路基本体段布置的预应力加固结构受列车动载影响甚微。 表10 预应力钢筋附加动应力峰值统计均值Table 10 Statistical mean value of additional dynamic stress peak of prestressed steel bars 1) 列车轴重越大,基床层动应力水平越高。受轨道不平顺的影响,左、右钢轨下路基面动应力峰值沿线路纵向分布存在显著差异。 2) 路基面动应力沿线路纵向的随机离散程度随列车轴重增大而增大,且预应力加固结构可在一定程度上控制动应力峰值沿线路纵向的离散程度,且轴重越大,控制优势越显著。 3) 采用变异系数和均值对两种路基结构基床层内不同深度处的动应力峰值数据进行统计分析,发现变异系数和平均值沿深度均是逐渐衰减的。在预应力加固结构作用下,预应力路基基床内动应力峰值的变异性得到改善,且列车轴重越大,改善效果相对越显著。 4) 基于柯尔莫哥洛夫-斯米洛夫(K-S)检验法,验证了两种路基在轨下基床层内不同深度的动应力峰值沿线路纵向均具有正态性。 5) 预应力钢筋振动响应程度沿坡面向下逐渐衰减,其时程曲线表现为由“三峰式”过渡为“单峰式”。而钢筋附加动应力远小于目标张拉应力,表明预应力钢筋受上部列车动载的振动影响程度低。
4 预应力钢筋附加动应力峰值统计分析

5 结论
