T型微带线传导干扰的时域建模分析方法

叶志红，张 玉，程亚军，鲁唱唱，李汸阳，詹超然

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引言

随着无线技术的快速发展,小型化和高集成度已然成为集成电路的发展方向。受集成电路电磁兼容性设计要求的制约,集成电路各元件和电路模块之间的互联线呈现多种弯折结构,T型微带线是其中较为常见的一类结构,当干扰信号流经T型微带线时,在连接节点处会出现电荷聚集效应,使得该点的阻抗特性发生变化。因此,开展T型微带线的传导干扰建模分析方法研究,准确计算干扰信号在T型微带线上的瞬态响应,可为集成电路板级信号完整性分析提供重要技术支撑。

目前,国内外学者基于传输线理论,提出了多种高效的数值算法,用于印刷电路板(Printed Circuit Board, PCB)上微带线的传导干扰分析。其中,Baum-Liu-Tesche(BLT)方程方法[1-5]和传输线方程的时域有限差分(Finite-Difference Time-Domain, FDTD)解法[6-10]应用最为广泛。

传统BLT方程方法基于电磁拓扑理论,通过节点和管道的形式建立集总干扰源与微带线连接节点及端接负载响应的联系,并对构建的关系矩阵进行求解得到负载上的电压和电流响应。但是,当集总干扰源为宽频带信号时,计算效率会急剧降低。同时,BLT方程只能获得端接负载上的电压电流,无法求取微带线沿线各点的电压,不利于后续开展二次辐射仿真。尽管频域BLT方程已被部分学者应用卷积运算扩展到了时域,但是卷积运算需要存储大量的历史时刻电压、电流数据,计算过程复杂且效率低下。传输线方程的FDTD解法是一类时域算法,其使用传输线方程构建微带线的传导干扰模型,并对传输线方程使用FDTD[11-12]的中心差分格式进行求解,获得微带线沿线及其端接负载的瞬态响应。然而,该方法尚未用于T型微带线这类特殊微带线结构的传导干扰建模与仿真分析。

因此,本文基于传输线方程,结合电荷守恒定律,并引入高阶FDTD(2,4)方法,研究一种高效的时域混合算法,在避免对T型微带线精细结构直接建模的情况下,实现T型微带线传导干扰的时域快速仿真。

1 时域混合算法理论

时域混合算法实现T型微带线的传导干扰分析,需要将T型微带线进行分解,形成多段独立的直微带线和连接节点结构,并分别使用高阶FDTD(2,4)方法和电荷守恒定律进行传导干扰建模与计算。下面将从直微带线传导干扰的高阶FDTD(2,4)求解和基于电荷守恒的连接节点电压计算两方面,详细阐述时域混合算法的具体实施方法。

1.1 直微带线传导干扰的高阶FDTD(2,4)求解

一般,微带线与接地板之间的距离小于干扰源最高频率对应的最短波长,可以忽略微带线的辐射效应。此时,应用传输线方程构建每段直微带线的传导干扰模型,表示为:

(1)

(2)

式中:I(y,t)、V(y,t)分别表示直微带线沿线各点的电流和电压,C、L分别表示直微带线的单位长度电容和电感,可使用有限元法对直微带线二维横截面进行建模并提取得到。

(3)

Vn+1(k)=Vn(k)-

(4)

式中:k表示各段直微带线上电压和电流沿线各点的位置,取值为2,3,…,N-2。

从式(3)和式(4)可以看到,FDTD(2,4)的迭代方式不适用于直微带线始端和终端的电压,以及始端和终端相邻节点处的电流和电压。因此,对于微带线两端电压需要使用前向差分和后向差分进行处理,其相邻节点处的电压电流,需要采用传统FDTD的中心差分格式进行求解,具体的迭代公式见文献[16]。

1.2 基于电荷守恒的连接节点电压计算

T型微带线的连接节点是各段直微带线的共用端口,节点处的电压无法使用传统FDTD或者高阶FDTD(2,4)的差分格式求解得到。T型微带线连接节点处的电荷守恒应用如图1所示,考虑到节点处的电压是连续的,因此使用电荷守恒定律构建连接节点处电压与各段直微带线上电流之间的关系方程,表示为:

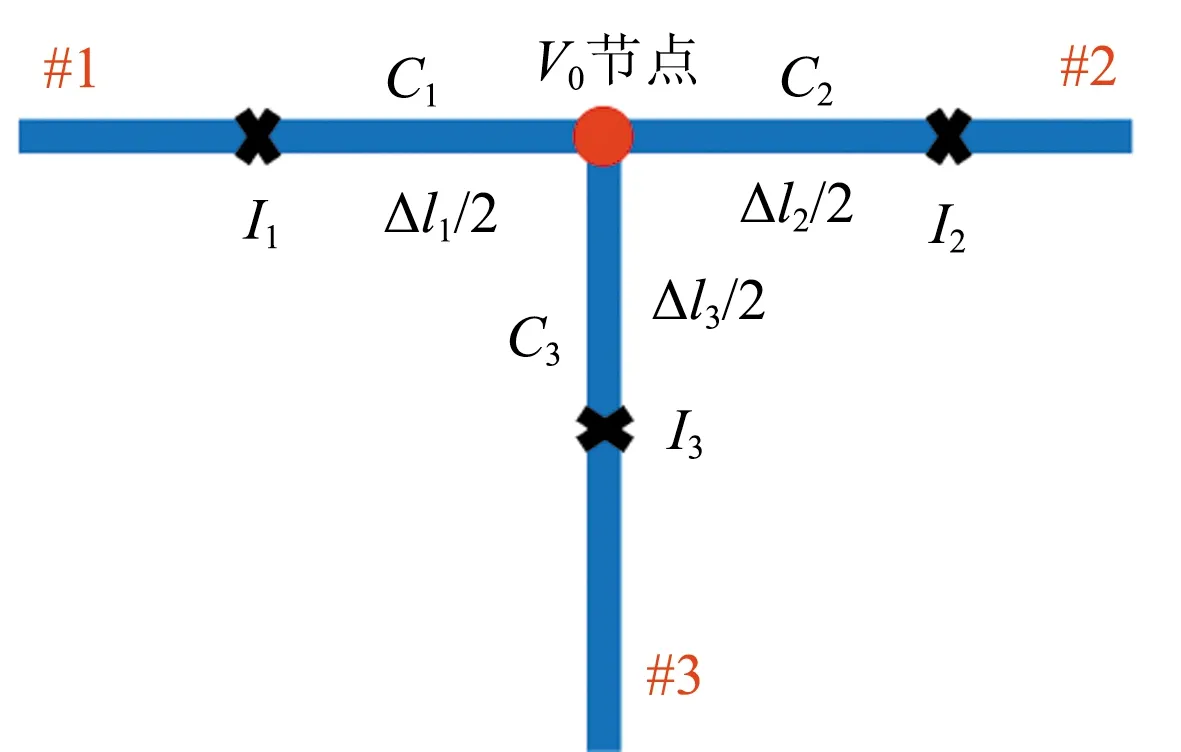
图1 连接节点处的电荷守恒应用Fig.1 Charge conservation application at connecting node

(5)

式中:V0为节点处的电压,Δl1、Δl2和Δl3分别为直微带线#1、#2、#3进行网格划分的空间步长,C1、C2、C3分别为直微带线#1、#2、#3的单位长度电容参数,I1、I2、I3分别为微带线#1、#2、#3上邻近连接节点的电流响应。

采用FDTD中心差分格式对式(5)进行离散,获得T型微带线连接节点处电压的迭代计算式为:

(6)

2 数值仿真分析

使用时域混合算法对单个T型微带线结构和多个T型微带线组成的网络结构进行传导干扰计算,并与BLT方程和电磁仿真软件CST的仿真结果进行对比,验证该算法的计算精度与效率。

单个T型微带线的传导干扰模型如图2所示,接地板设为理想导体,基板大小为5 cm×6 cm,厚度为1 mm,材料的相对介电常数为5。T型微带线位于基板上表面,由3段直微带线#1、#2、#3构成,长度分别为4、2、3 cm,宽度为2 mm,厚度为0.034 mm。微带线#1始端接有高斯脉冲电压源,幅度为10 V,脉宽为4 ns。直微带线#2、#3的端接负载为R1=R2=50 Ω。使用有限元法对直微带线对应的二维横截面进行建模,提取得到的直微带线单位长度电感和电容分布参数分别为L=290.22 nH和C=143.09 pF。

图2 单个T型微带线的传导干扰模型Fig.2 Conducted interference model of a single T-shaped microstrip line

BLT方程、CST和时域混合算法仿真得到的负载R2上的电压响应如图3所示。为了更加客观地评价时域混合算法的精度,使用特征选择评估(Feature Selective Validation,FSV)方法[17-18]对3种方法的仿真结果进行幅度差异分析。BLT方程和时域混合算法的计算结果与CST仿真结果的幅度差异量(Amplitude Difference Measure,ADM)直方图如图4所示。可以看出,时域混合算法与CST仿真结果的幅值吻合度达到很好以上等级的比例为100%,而BLT方程仅为90%,验证了该算法的精度能够与CST全波仿真保持完全相同,且优于BLT方程。

图3 3种方法计算得到的负载R2上的电压响应Fig.3 Voltage responses on the load R2 calculated by the three methods

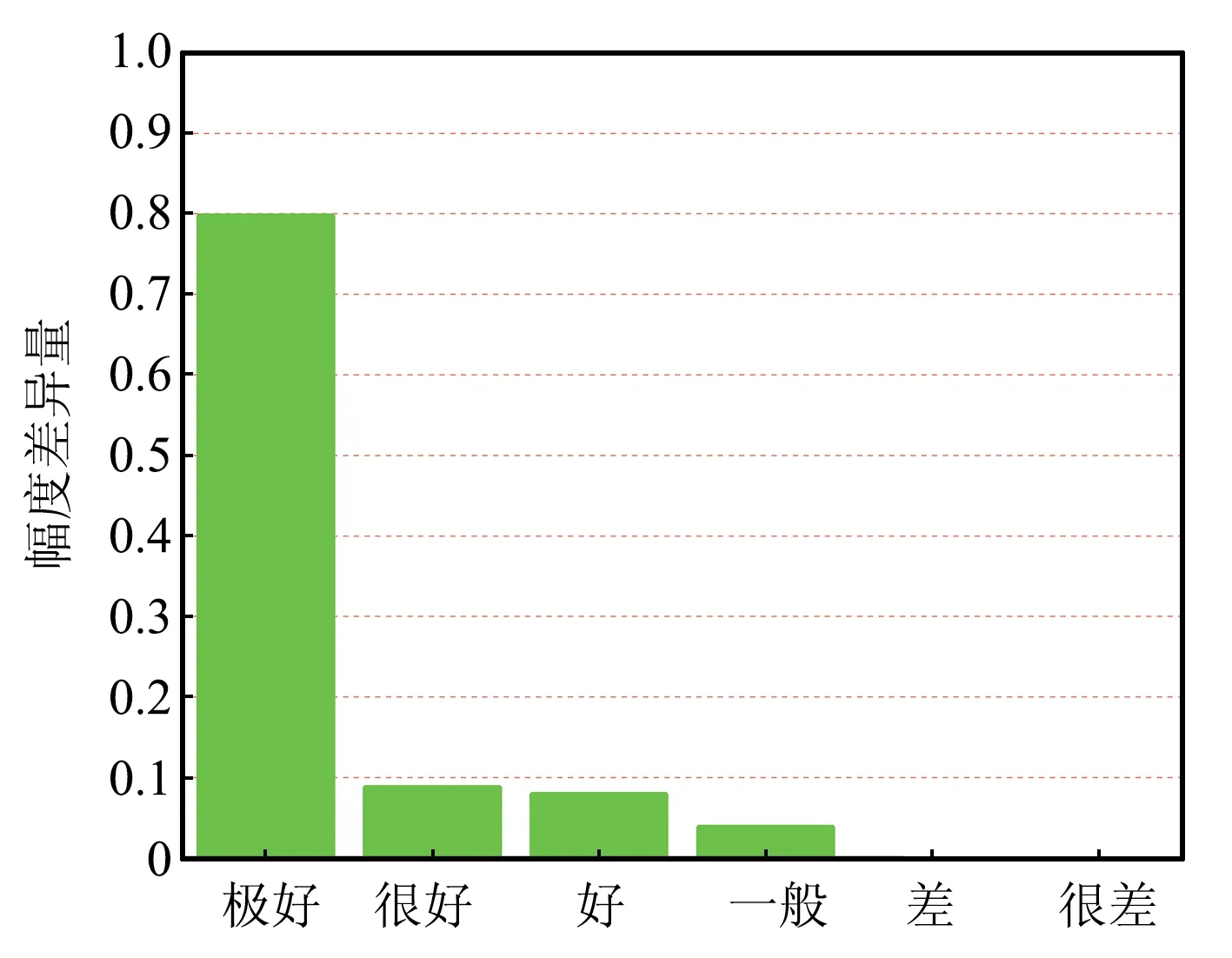
(a)BLT方程与CST仿真结果的ADM直方图

(b)时域混合算法与CST仿真结果的ADM直方图图4 3种方法计算得到的负载R2电压的FSV评估Fig.4 FSV evaluation of the voltages of load R2 calculated by the three methods

由于BLT方程是一种频域算法,对于宽频带串扰问题,需要重复多个频点的计算以后,通过逆傅里叶变换得到负载电压的时域响应,此过程需占用较多无用时间,因此未对BLT方程的计算时间进行统计。CST和时域混合算法计算所需网格量和时间的对比如表1所示,可以看出,在激励源持续时间一致的情况下,时域混合算法的计算时间缩短为CST的1/16。原因是,虽然CST全波仿真使用自适应网格可以减少对PCB基板和微带线精细结构的剖分网格量,但是时域混合算法只需对微带线沿线划分网格,且无需对基板结构直接建模,相较于CST,节省了大量的网格量而大大降低了内存需求和计算时间。

表1 时域混合算法与CST所需网格量和时间的对比Tab.1 Comparison of the grid number and cost time required by the time domain hybrid method and CST

为进一步验证时域混合算法的置信度,将其应用于复杂T型微带线级联网络的传导干扰分析,对应的T型微带线网络的传导干扰模型如图5所示,整体网络按照3个连接节点,可以分解为7段直微带线,标记为#1～#7。介质基板和集总电压源的参数设置均与上述算例相同。微带线#2、#4的长度分别为2、6 cm,其余微带线的长度均为3 cm。网络端接负载为R1=R2=R3=R4=50 Ω。

图5 T型微带线级联网络的传导干扰模型Fig.5 Conducted interference model of T-shaped microstrip line cascade network

时域混合方法和CST计算得到的负载R2和R3上的电压响应如图6所示,同样,采用FSV方法对2种方法的仿真结果进行幅度差异评估,得到对应的ADM直方图如图7所示。可以看出,2种方法的计算结果在幅值吻合度上达到很好以上等级的占比仍能保持100%。

(a)R2上的电压

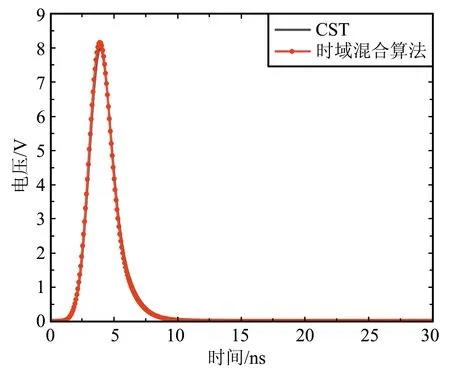
(b)R3上的电压图6 T型微带线网络不同负载的电压响应Fig.6 Voltage responses on different loads of T-shaped microstrip line network

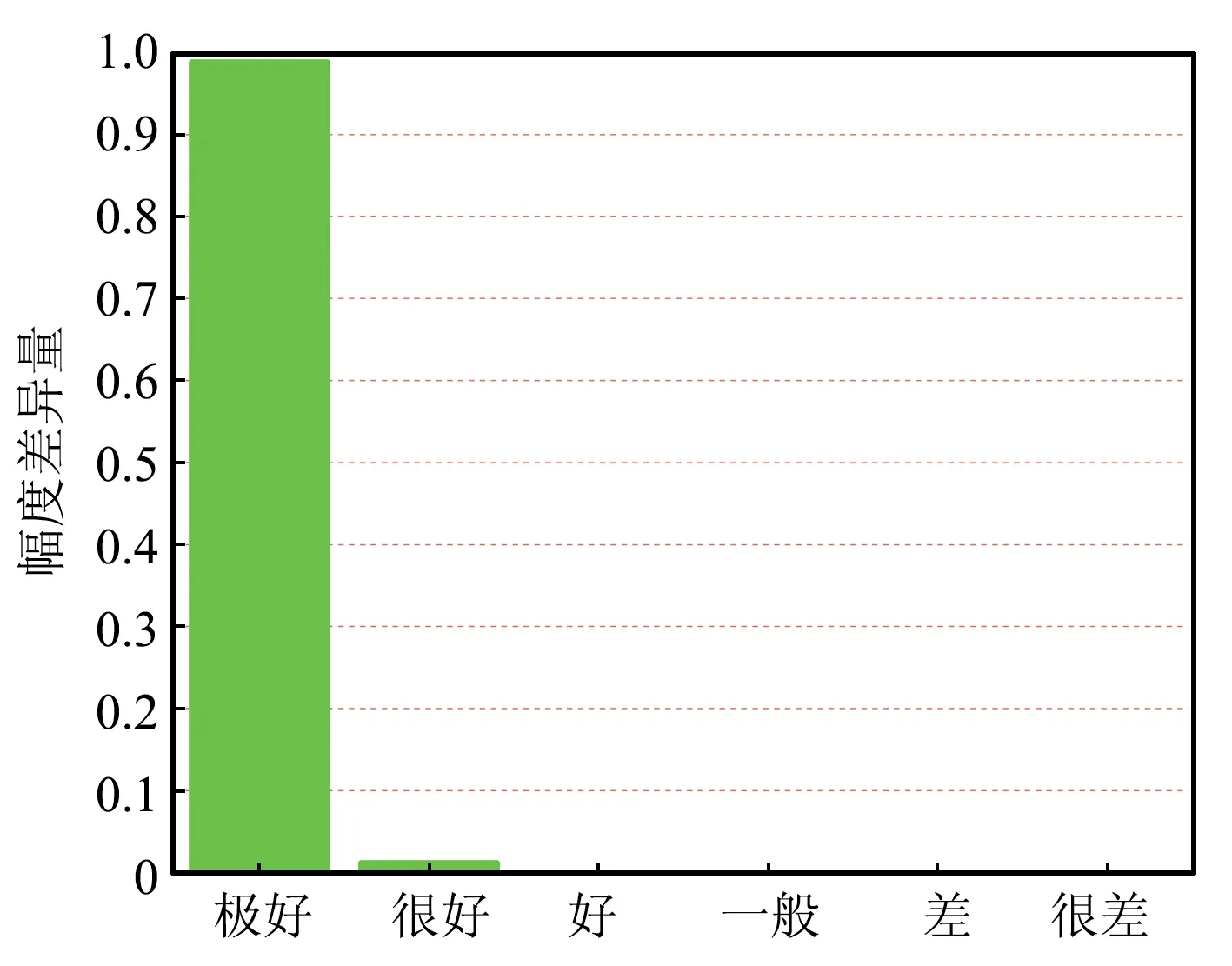
(a)R2上电压的ADM

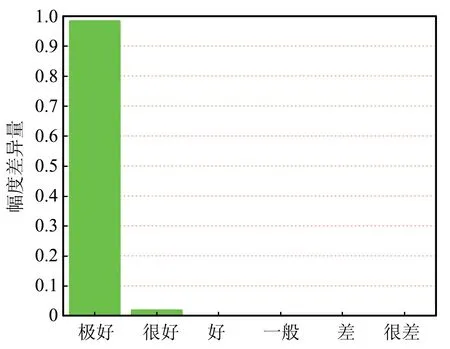
(b)R3上电压的ADM图7 T型微带线网络不同负载电压的FSV评估Fig.7 FSV evaluation of the voltages on different loads of T-shaped microstrip line network

3 结束语

针对集成电路上T型微带线的传导干扰,将传输线方程与高阶FDTD(2,4)和电荷守恒定律相结合,研究了一种高效的时域混合算法。该方法将T型微带线分解成多段直微带线和连接节点,采用传输线方程结合高阶FDTD(2,4)快速求解各段直微带线的传导干扰响应,并在连接节点处应用电荷守恒,求解节点处的电压响应。该时域混合算法能够与CST全波仿真保持相同的计算精度,而且无需对T型微带线的精细结构直接建模,使用高阶FDTD(2,4)的大空间步长进行迭代求解,相较于全波算法可以节省大量计算时间。