基于改进SIFT的无人机影像匹配方法
2023-10-12王瀚铮
王 一,齐 皓,王瀚铮,程 佳
(1.华北理工大学 电气工程学院,河北 唐山 063210;2.唐山市金属构件产线智能化技术创新中心,河北 唐山 063210)
0 引言
近些年,无人机遥感技术广泛应用于城市建模、资源调查和地形勘测等多个领域,具有获取空间影像分辨率高、灵活性强和实时传输等优点[1]。但在航拍过程中,由于无人机受自身飞行高度、相机视角等参数的限制,使得所拍摄的影像视野较小,无法显示更完整的信息,成像视差严重且存在较大的几何变形,从而导致影像匹配的效果不佳,因此如何实现无人机影像的特征匹配具有重要研究意义。现阶段的影像匹配方法主要分为基于区域的方法和基于特征的方法两大类[2]。基于区域的方法利用图像的灰度信息寻找图像中的同名点实现匹配。由于无人机影像数据的不稳定性,通过影像灰度进行匹配往往达不到预期的效果,且计算量大、处理时间过长,对无人机影像不太适用。
基于特征的匹配方法因其稳健、快速被广泛应用于无人机影像的匹配。Lowe[3]提出了尺度不变特征变换(Scale-Invariant Feature Fransform,SIFT)算法,这种算法具有很强的提取特征点的能力,能克服一定的尺度、旋转及模糊变化。然而,SIFT算法最初是针对光学图像开发的[4],直接应用于灰度差异较大的大幅面遥感影像时很难找到足够多的正确匹配对[5]。传统SIFT算法特征描述子过多、计算复杂、耗时巨大,因此Bay等[6]改进了SIFT的描述方式,将128维描述符改为64维,匹配效率有所提高,但其实时性仍无法满足实际场景需求。
针对以上匹配算法运行时间长的问题,Ke等[7]提出PCA-SIFT算法,把SIFT特征描述子从128维降到了20维,速度有所提高但低维度的描述符描述能力较差,应用于高分辨率的无人机影像时准确率较低。上述算法通过减少描述符维度的方式来解决耗时长等问题,但并没有改变浮点型描述符冗余的数据结构。Rublee等[8]在2011年提出ORB算法,该算法采用FAST算子[9]进行检测并在特征描述阶段使用BRIEF[10]二进制描述符,同时利用图像金字塔和灰度质心法实现了尺度、旋转不变性,该算法抛弃了浮点型描述符,采用二进制描述结合汉明距离进行匹配,相比SIFT、SURF算法,ORB算法的匹配速度大大提高[11],然而基于手动设计的二进制描述符区分性比浮点型描述符差,匹配能力欠佳。
为了提高影像匹配的运行效率,一些改进方法被提出用于解决上述问题。马耀名等[12]提出一种基于高斯曲率滤波的无人机航拍图像匹配方法,该方法首先使用高斯曲率滤波构建图像金字塔,提取不同尺度的描述符两两做差,获得了较多的正确匹配点,但只适用于实时性较低的场景。郭丽等[13]提出采用SIFT算法和FSC算法相结合的方式剔除遥感图像局外点,匹配点对分布均匀但数量较少。陈保宇等[14]基于KAZE算法对露天煤矿的无人机影像进行匹配,正确匹配率较高但耗时较长。
无人机影像匹配不仅要保证较高的正确匹配率,还要拥有较快的匹配速度。因此针对无人机影像存在成像视差严重、噪声多的问题,首先采用联合双边滤波对原始图像进行降噪预处理,提高图像质量,并且针对传统SIFT算法在匹配高分辨率无人机航拍影像时运行速度慢、匹配正确率低的问题,提出从SIFT算法中第二组尺度空间进行特征检测;采用基于机器学习的二进制描述算法强化描述符(Boosted Efficient Binary Local Image Descriptor,BEBLID)[15];通过Vicinity-KNN算法对特征点进行粗匹配,减少算法迭代次数,最后引入自适应局部仿射匹配算法[16]进行特征匹配的优化,以提高无人机影像的匹配精度和效率。
1 改进的SIFT算法
1.1 联合双边滤波预处理
在对图像进行特征匹配之前,首先要对原始的图像进行预处理,以消除无关的信息,最大程度地简化数据,使特征点检测更加均匀,便于计算机进行识别和处理[17]。联合双边滤波是一种非线性的滤波器,可以达到保持边缘、降噪平滑的效果。
联合双边滤波可以表示为:
(1)
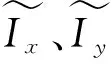
联合双边滤波使用一幅导向图作为值域权重的计算依据。为了提高算法的效率,首先对原始图像进行下采样处理,然后将处理后的图像按照最邻近插值的方式上采样至原图大小,从而快速实现对一幅图像的联合双边滤波。
1.2 SIFT特征提取
在图像预处理的基础上,利用SIFT算法进行特征提取得到稳定准确的特征点。
① 尺度空间的建立
一幅图像的尺度空间L(x,y,σ)是由一个变化尺度的二维高斯函数G(x,y,σ)与初始图像的li=1卷积运算所决定的:
L(x,y,σ)=G(x,y,σ)*I(x,y),
(2)
(3)
式中:σ为尺度参数,(x,y)为图像的像素坐标,*表示卷积运算。
② 改进尺度空间极值点检测
采用高斯微分 (DOG)函数,构建高斯差分金字塔D(x,y,σ)以实现特征点的检测:
D(x,y,σ)=L(x,y,kσ)-L(x,y,σ),
(4)
检测部分与SIFT算法类似,各检测点分别与目标点相邻的26个像素点进行对比。但与SIFT算法不同的是,为提升算法的匹配效率,高斯金字塔的初始层并不采用扩展后的输入图像,而是使用原始图像,并从第2组尺度空间开始进行检测,如图1所示。
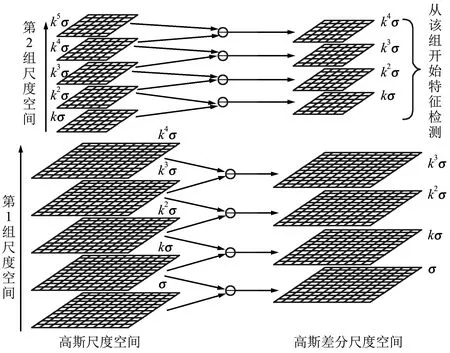
图1 改进尺度空间极值点检测示意Fig.1 Improved schematic diagram of scale space extreme point detection
③ 去除边缘不稳定特征点
主曲率在边缘方向的值较大,因此主曲率可通过Hessian矩阵求出:
(5)

1.3 BEBLID特征描述子
SIFT算法使用一组128维的特征向量来描述关键点,产生特征描述子,进行后续的匹配。但其计算量大,导致特征点冗余、耗时较长,无法满足实时性要求。ORB算法基于手工设计二进制描述子,采样方式的建立依靠经验和实验验证,使其在实际应用中受到了很大的限制。为此,本文首次提出将基于机器学习的BEBLID算子与改进的SIFT算法相结合,提取特征描述符。
为使二进制描述符在获取匹配速度优势的同时具有浮点型描述符强鲁棒性和强区分性的优点,BEBLID使用AdaBoost算法[18]进行改进,在Brown数据集[19]上进行训练,使所有弱学习器共享一个相同的权重进而得到二进制描述符。定义损失函数和特征提取函数如下:
(6)
式中:λ为弱学习器权重,h(x)为弱分类器,其中hk(z)≡hk(z;f;T)由特征提取函数f(x)和阈值T来定义弱学习器。
(7)
(8)
式中:I为任意像素的灰度值,R(p1,s)、R(p2,s)分别为像素点p1、p2在邻域s×s内的灰度值之和。
BEBLID算子提取描述符工作流程如图2所示,使用基于机器学习的采样模板(图中的蓝色和黄色方框)在该邻域内采样,通过特征提取函数f(x)计算蓝色方框和红色方框内像素平均灰度值的差,并与阈值T做比较,若大于T则为1,反之为-1。然后归一化形成具有强描述性的二进制描述符。
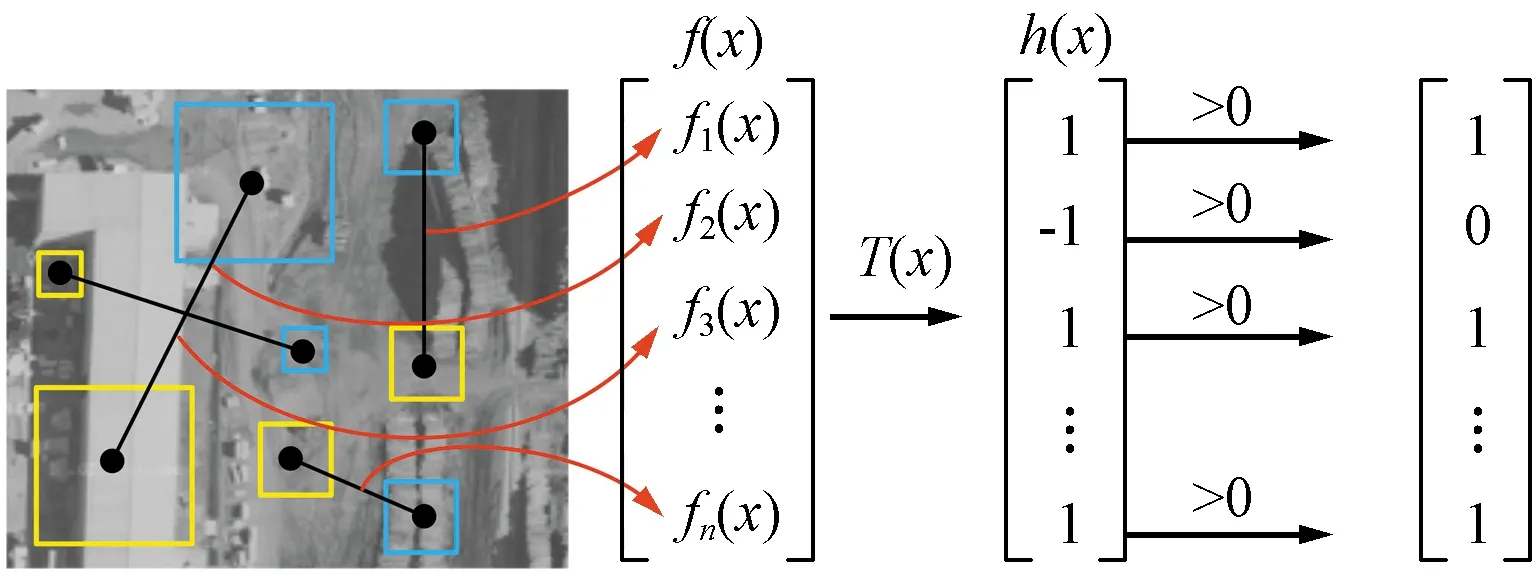
图2 BEBLID提取描述符工作流程Fig.2 BEBLID extraction descriptor workflow
2 特征点粗匹配与误匹配点滤除
2.1 Vicinity-KNN算法粗匹配
传统KNN算法是从所有训练样本中寻找距离未知样本最近的K个样本,将K个样本中出现最多的类别赋给未知样本[20]。然而这种方法需要每次都遍历待匹配图像的所有特征点,耗时较长。
因此,利用图像的邻域信息改进KNN算法,在特征匹配时增加运动平滑性约束,缩小特征匹配区域。正确的匹配在运动空间中是平滑的,运动平稳相邻的特征在运动空间中具有一致性[21],所以相邻特征点对应的匹配特征点的区域也是相邻的。从而,参考图像中的特征点搜索出待配准图像中与之匹配的特征点后,该特征点邻域内的所有特征点只需在待配准图像中匹配点的邻域内进行搜索即可。同时,为方便邻域的选取,在匹配时引入网格结构,将样本图像均匀划分为n×n网络,以网络为单位进行匹配。匹配示意如图3所示,假设特征点A的待匹配点为点B,则与点A在同一邻域内的特征点O只需在特征点B的3×3邻域内搜索匹配点,从而缩短匹配时间,提高匹配速度。

图3 特征匹配示意Fig.3 Feature matching diagram
2.2 匹配点精匹配
粗匹配中存在大量的误匹配点,影响了匹配精度。传统的误匹配剔除算法常采用随机采样一致性(RANSAC)算法[22],但RANSAC计算参数不存在迭代次数的限制,且需要人为设定阈值,容易导致出现错误的结果,为此本文引入一个新的误匹配点滤除算法。
首先需要输入初始假定匹配集合,为每个关键点分配一个置信度分数,然后在半径R内选取具有置信度分数最高的点作为种子点,并为每个种子点都在初始匹配集合中找到相对应的匹配点。
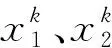
(9)
式中:k为匹配关系,rk为残差值。
算法是对局部邻域内进行仿射变换估计,不同的邻域包含不同的仿射变换模型,所以无法得到一个固定的阈值适用于所有种子匹配点对应的邻域。因此采用一种基于假设检验的方式[23]来判断候选匹配点是否为正确匹配点,假设所有离群点都符合均匀分布,将残差集合R中的残差项rk映射到置信度ck:
(10)
式中:H0是包含统一外点的假设,正样本计数P=|l:r1≤rk|为假设对应k最差匹配关系下的内点的数量,R表示所有候选匹配点残差值集合,从0开始对k进行标序时P=k+1。当置信度超过某个阈值tc时,则判断为正确匹配点,反之进行剔除。在每次迭代过程中都要对上述残差、置信度以及内点进行修正,然后使用先前获得的内点去拟合新的仿射矩阵,再进行检验,直至达到最大的迭代数,最终输出内点。
3 方法验证及分析
实验在AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz CPU,16 GB内存,Windows 10操作系统,Pycharm环境,OpenCV3.4.2计算机视觉库下,实现算法的调试。为了验证所提方法的可行性,将本算法与ORB算法、传统SIFT算法、改进SIFT(ISIFT)算法[24]和改进KAIE(IKAZE)算法在Oxford VGG标准图像数据集和4组典型区域的无人机影像数据进行匹配实验。ISIFT算法将特征点的矩阵区域改为圆形,从而降低了算法的复杂度。
借助绝对距离和余弦相似度进行双重匹配,最后通过RANSAC算法对错误的匹配点对进行过滤。
3.1 标准图像数据集实验
实验采用Oxford VGG标准图像数据集中Wall、Boat、Leuven、Tree和Ubc五组图像作为实验图像,每组图像共6张,变化程度依次不断加强,对应图像如图4所示,其中图4(a)~图4(e)分别表示视点变化、旋转变化、光照变化、模糊变化和JPEG压缩。

图4 Oxford实验图像Fig.4 Oxford experimental images
采用正确匹配率(Correct Matching Rate,CMR)和运行时间等评价指标对图像匹配算法进行综合评价。CMR定义为:
CMR=mc/m,
(11)
式中:mc为匹配正确的点数,m为所有匹配对数。
图5展示了分别使用ORB、SIFT、ISIFT、IKAZE和本文所提方法对图4数据进行匹配的用时和正确率比较。分别用每个数据集的第一幅图像依次与后面5幅图像进行匹配,得到不同算法的平均正确匹配率和平均匹配时间。由图5(a)可以看出,IKAZE算法的匹配时间最长,而本文算法的匹配速度仅次于ORB算法,相比于SIFT算法有较大的优势。这主要是因为在特征提取时,跳过了无用特征点较多的第一组尺度空间,减少了特征提取的计算量,并采用二进制描述子进行描述,同时Vicinity-KNN算法大大减小了算法的复杂度。图5(b)展示了不同算法在不同条件下的正确匹配率,即CMR,正确匹配点数与所有匹配对数之比,CMR越高,代表算法的匹配效果越好。IKAZE算法使用FREAK二进制描述符[25]代替浮点型描述符并通过RANSAC算法剔除错误匹配点,增加了算法匹配效率,但降低了稳定性。本文算法网格密度为10×10,从图5(b)可以看出,本文算法相比于其他几种算法在视点、光照、模糊、图像压缩变化条件下正确匹配率较高。
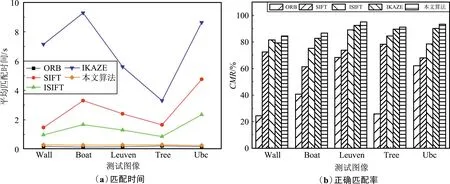
图5 Oxford数据集运行结果示意Fig.5 Schematic diagram of Oxford dataset operation results
3.2 无人机影像匹配及结果分析
影像匹配是无人机影像处理的重要步骤,直接影响后期构建地形图和三维重建的精度。为了测试所提方法在无人机影像匹配中的性能,选取UAV-image-mosaicking-dataset数据集[26]进行匹配实验,该影像由KC1600无人机搭载SonyNEX-7相机捕获,分别包含61、182、51张图像。相机焦距35 mm,每张图像的分辨率为3 680 pixel×2 456 pixel,平均飞行高度为558、405、988 m。选取部分影像如图6所示,其中图6(a)和图6(d)的地形高程变化很明显,而其他2个影像的变化相对较小。图6(a)中的地形高程为62~169 m,图6(b)、图6(c)的高程差小于25 m,图6(d)的高程变化最大,为354~507 m。

图6 无人机影像数据集Fig.6 UAV image dataset
SIFT和本文算法匹配效果对比如图7所示,左图为经RANASAC算法提纯后SIFT算法匹配效果图,右图为本文算法匹配效果图,其中图7(a)~图7(d)分别表示相应变化条件下的匹配效果。从图7可以明显看出,该无人机影像含有较多的相似干扰点,改进前的SIFT算法特征匹配点对较少,尤其是在边缘和细节特征不明显的影像中存在大量的匹配偏差和误匹配,而本文所提方法特征匹配点对分布均匀,能够正确、精准地完成影像的特征匹配。

为了显示所提方法具有明显优势,对本文及其他4种算法所获得的实验数据做进一步的整理和分析。不同算法的匹配时长如表1所示。

表1 不同算法的匹配时长Tab.1 Comparison of matching times for different algorithms 单位:s
为了看起来更直观,图8展示了各种算法运行匹配时间对比折线图。可以看出,对于以上5组数据,ORB算法用时最短,本文算法次之,依次是ISIFT算法、SIFT算法、IKAZE算法。IKAZE算法虽使用二进制描述符但需要迭代计算解非线性方程,因此匹配速度较慢。ISIFT、SIFT算法均采用浮点型描述符,基于欧式距离进行相似性计算,且使用基于KNN的匹配算法,故运行时间较长。ORB算法尺度空间和描述符构建比较简单,匹配速度最快。本文算法从第2组尺度空间开始特征检测与描述,减少了特征提取的工作量。同时,Vicinity-KNN算法减少了搜索特征点的迭代次数。因此,特征匹配的效率得到了显著提高。

图8 无人机影像数据集运行结果示意Fig.8 Schematic diagram of UAV image dataset operation results
图8(b)展示了各种算法在不同场景下运行的正确匹配率,可以看出本文所提方法的效果较好,其中ORB算法的CMR为57.94%,SIFT算法的CMR为69.59%,匹配率均较低。ISIFT算法采用绝对距离和余弦相似度相结合的方式进行匹配,最后通过RANSAC算法进行特征精匹配,匹配率略高于传统SIFT算法,为76.39%。IKAZE算法的CMR为83.54%。本文算法能够在保持较少的运行时间下,使准确率也得到保障,CMR为87.86%,相比于传统SIFT算法提升了18%,为复杂环境下无人机影像配准提供了保证。
4 结束语
针对传统SIFT算法在无人机影像匹配中错误率较高、运行速度慢的缺陷,提出了一种改进SIFT的无人机影像匹配方法。为减少噪声对无人机影像匹配的影响进行联合双边滤波预处理,然后从第2组尺度空间进行特征提取,有效减少了特征提取的计算量;在特征描述方面,首次引入BEBLID与ISIFF算法相结合,显著提高了运行速度;在特征匹配阶段增加运动平滑性约束,利用邻域信息改进KNN算法,对特征点进行初步匹配,结合自适应局部仿射匹配算法实现精匹配,保障了算法的鲁棒性。通过在标准图像数据集和无人机影像数据集上进行多次实验验证,本文算法在保持较高正确匹配率的基础上极大地缩短了运行时间,提取特征点分布更加均匀,可满足无人机影像匹配的需求。
