基于轨迹灵敏度的频率协调控制参数影响分析

田政鳞, 王正宇

(华南理工大学 电力学院,广东 广州 510641)

0 引 言

以风电为代表的新能源通过电力电子装置接入电网,其频率响应特性与常规同步机组相比存在较大差异:一方面,为促进电能的消纳利用,新能源运行于最大功率追踪点,没有备用容量参与系统调频;另一方面,由于转子侧与系统频率完全解耦,其风机的旋转动能完全被隐藏,无法进行惯量响应。随着新能源占比的逐渐提高,系统惯量水平和一次调频能力逐渐降低,系统频率稳定面临巨大威胁。

针对系统惯性支撑不足的问题,以新能源、储能和直流输电为代表的快速频率响应(fast frequency response,FFR)资源能够响应系统频率突然变化而快速调节有功注入,以减小扰动后频率的快速变化,缓解系统一次调频压力［1］。在此基础上,频率协调控制综合了虚拟惯量控制和频率下垂控制,可以同时模拟同步机组的惯量响应和一次调频特性,实现FFR资源惯量响应和一次调频的协调作用,增强高新能源占比电力系统的频率稳定性［2］。

FFR资源的惯量支撑和一次调频能力由频率协调控制的参数所决定。受调频备用容量的限制,参数选择是否合理将直接影响到FFR资源调频性能的发挥。因此,研究控制参数对频率动态特性的影响机理具有重要的现实意义。

关于控制参数对频率动态的影响分析方面,现有研究侧重于通过时域仿真方法展开定性讨论。如文献［3-7］通过对比虚拟惯量控制和频率下垂控制在不同投入情况下的频率动态特性,分析了不同控制策略的影响效果。文献［8-9］进一步研究了虚拟惯量和频率下垂系数对频率动态特性的影响。然而,上述文献并未提出表征参数影响程度的量化指标及量化分析方法。

为此,本文首先建立了考虑频率协调控制的系统频率响应模型,引入了轨迹灵敏度的分析方法,根据轨迹灵敏度在时域上的分布及其变化情况,从影响时间、影响方式和影响程度三个方面分析各控制参数对频率动态特性的影响;然后,基于轨迹灵敏度识别了频率最低点的主导影响因素,并提出了改善频率最低点的控制参数调整策略;最后,基于MATLAB/Simulink程序,验证了所提参数影响分析方法和调整策略的正确性和有效性。

1 考虑频率协调控制的系统频率响应模型

1.1 频率协调控制的控制原理

同步机组转子动能可直接响应系统频率变化,发生有功扰动时,其旋转惯性具有阻尼频率变化的作用。通过引入虚拟惯量控制,FFR资源能响应频率的变化速率,经虚拟惯量系数快速调节FFR资源的有功输出,从而模拟出同步机组的惯量支撑作用。其原理表示为:

(1)

式中:ΔPi为虚拟惯量控制功率;Ki为虚拟惯量系数;Δf为系统频率变化量。

同步机调速系统通过调节有功输出参与一次调频,其功频静态特性反映了一次调频的能力。同理,通过引入频率下垂控制,FFR资源能响应频率的变化量,经频率下垂系数快速调节FFR资源的有功输出,从而模拟出同步机组的一次调频作用。其原理可表示为:

ΔPd=-KdΔf

(2)

式中:ΔPd为频率下垂控制功率;Kd为频率下垂系数。

综上所述,在考虑FFR资源频率协调控制下,将系统等值聚合为单机带集中负荷模型,并保留原动机-调速器系统,可以得到系统频响应模型,如图1所示。

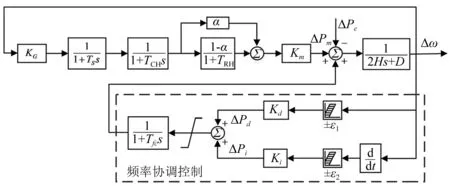
图1 考虑频率协调控制的系统频率响应模型

图1中:KG为功频静态特性系数;TS为调速器时间常数;TCH为蒸汽容积时间常数;α为高压缸功率占比;TRH为再热器时间常数;Km为机械功率增益系数;H为等效惯性时间常数;D为等效阻尼系数;ΔPm为汽轮机机械功率变化量;ΔPe为发电机电磁功率变化量;Tfc为频率协调控制的时间常数;ε为死区环节,取±0.033 Hz。

1.2 系统频率响应模型的等效调频参数

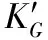
(3)

式中:SB(SG)为常规同步发电机总额定容量;SB(RE)为新能源总额定容量。

频率协调控制所模拟出的惯量支撑和一次调频能力主要由其控制参数决定,其常见的整定方法是模拟同步发电机的惯量响应特性和一次调频特性,原理如下所示。

(4)

通过增大Ki和Kd,频率协调控制理论上可以模拟出比同容量同步机组更大的惯量支撑和一次调频能力。然而,FFR资源需同时提供参与一次调频和惯量响应的有功功率,相比同容量同步机组有更大的备用容量需求。此外,为促进电能的消纳利用,往往会对FFR资源参与调频的备用容量加以限制,因此频率协调控制参数不能进行大范围变化。

2 频率协调控制参数的轨迹灵敏度分析

2.1 轨迹灵敏度与区间轨迹灵敏度

不同于通常在运行点对模型进行线性化的常规灵敏度,轨迹灵敏度是轨迹关于参数的导数,是反映系统中某一参数、结构发生微小变化时动态轨迹的变化程度,常用于分析参数变化所导致的系统轨迹变化。

参数摄动法求解轨迹灵敏度时无需对系统进行线性化处理,可以不涉及系统的物理本质和结构特点,能适用于复杂的黑箱系统,避免了解析法的复杂数值积分计算。其原理如下:

电力系统的动态过程可以用微分-代数方程组描述:

(5)

式中:x为状态变量;y为代数变量;u为系统参数。

假设该系统状态变量的解为:

x(t)=φx(x0,t,u)

(6)

式中:x0为状态变量初始值。对上式关于u进行泰勒展开,并忽略Δu的高阶项,可得:

(7)

式中:xu(t)为状态变量x关于参数u的轨迹灵敏度。

当Δu足够小时,使用中心差分公式可以得到轨迹灵敏度近似计算方法,如式(8)所示。

(8)

当系统参数u在一个区间范围内变化时,可以通过区间平均值的概念描述参数u在区间内变化时对函数x(t)的平均影响程度。将参数u的变化区间［a,b］等分为n个间距点,计算参数u在每个间距点上的轨迹灵敏度,并采用该区间内轨迹灵敏度的平均值来表征参数u在区间内变化时对函数x(t)的平均影响程度。相应地,区间轨迹灵敏度可以定义为:

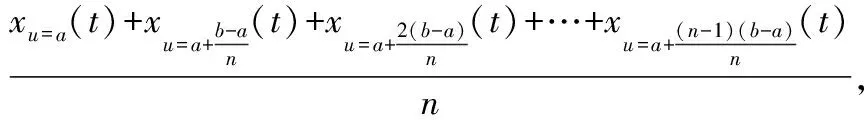
(9)

可以看出,间隔点n的数量越大,区间轨迹灵敏度就能越好地描述参数u在区间内变化时对函数x(t)的平均影响程度,但计算量也会相应增大。

针对舍饲羊群中单体羊只的免疫接种工作一定要做到严格谨慎执行，如临时接种、紧急接种等工作都要按照规章制度实施，保证羊只的免疫情况均实现登记造册，并制定一系列的免疫程序。结合国家的重大动物疫病强制免疫体系进行合理化安排部署，保证舍饲羊群疫病程序化免疫接种工作流程顺利开展。目前，上庄乡专门针对舍饲羊群的羊痘、羊支原体肺炎等免疫疫苗开展接种工作，确保地方舍饲羊群的健康成长。

2.2 频率协调控制的轨迹灵敏度分析

频率响应模型的数学解析计算较为复杂,借助参数摄动法求解系统频率对控制参数的轨迹灵敏度,可以量化分析各控制参数变化对频率动态响应的影响程度。频率协调控制参数的轨迹灵敏度可以表示为:

(10)

式中:δ为步进步长,本文取0.001。

控制参数的轨迹灵敏度可定量表征控制参数变化对频率动态响应特性的影响,其正负号反映了参数变化时频率动态轨迹的变化方向,其大小反映了控制参数变化时频率动态轨迹的变化幅度,其时域分布情况反映了控制参数变化的影响时间。

2.3 考虑频率最低点的控制参数调整策略

电力系统的频率控制中往往最关注频率的最低点,频率最低点受惯量水平和一次调频的共同影响。虽然增大Kd和Ki均能提升FFR资源的调频能力,但受备用容量的约束,控制参数取值具有范围限制。通过合理调整控制参数的取值,可以提高FFR资源的调频效果。因此,基于控制参数的轨迹灵敏度,可以得到针对频率最低点的控制参数调整策略。

(1) 在控制参数的取值区间内,计算频率最低点对各控制参数的区间轨迹灵敏度。

(2) 比较虚拟惯量系数和频率下垂系数的轨迹灵敏度大小,识别对频率最低点影响程度最大的主导影响因素,并优先对主导控制参数进行调整。

若控制参数的取值区间较大,可以将其划分为数个子区间,依次重复上述步骤。

3 仿真分析

3.1 仿真系统

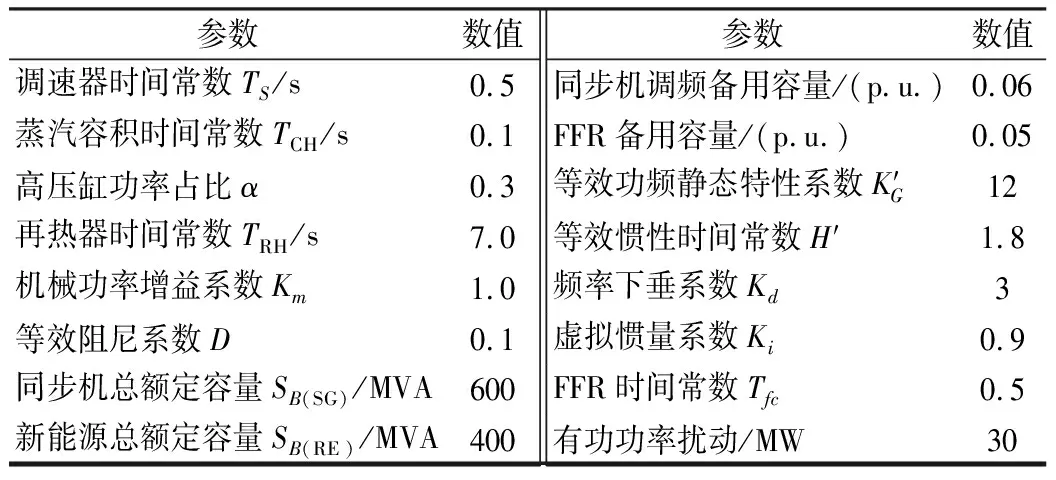
表1 系统频率响应模型参数设置

3.2 案例分析

基于上述仿真系统,分别对无频率控制、仅频率下垂控制、仅虚拟惯量控制和频率协调控制四种FFR资源控制策略下的频率动态特性进行对比分析,结果如图2所示。

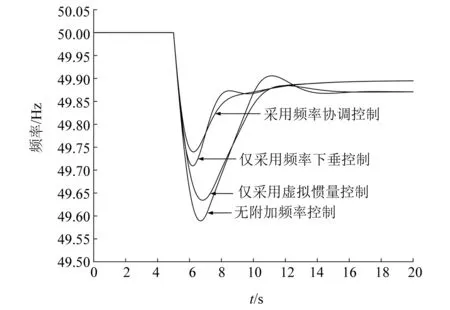
图2 不同控制策略下频率动态特性对比

可以看出,虚拟惯量控制减缓了频率的快速变化,减小了频率跌落速度的同时也减缓了频率的恢复速度,且未能响应频率的稳态偏差;频率下垂控制响应频率的偏差量,对频率的下降和恢复均具有改善作用,同时也能减小频率的稳态偏差。

为进一步揭示控制参数对系统频率动态响应的影响机理,根据式(10)分别计算系统频率对虚拟惯量系数Ki和频率下垂系数Kd的轨迹灵敏度,结果如图3所示。

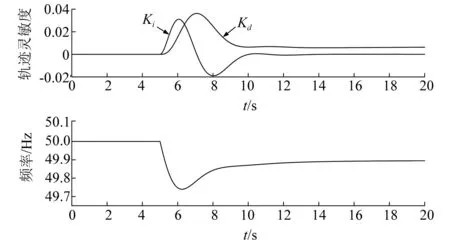
图3 频率协调控制参数的轨迹灵敏度

从轨迹灵敏度在时间上的分布来看,虚拟惯量系数的变化只对频率动态变化过程产生影响,而在频率稳态阶段其轨迹灵敏度为零,不影响频率的稳态特性。通过增大虚拟惯量系数可以减缓频率的跌落速度,但也会减缓频率的恢复速度,增强对频率变化的阻尼作用。频率下垂系数的轨迹灵敏度分布滞后于虚拟惯量系数,主要作用于频率恢复过程直到进入新的稳态。通过增大频率下垂系数可以加快频率的恢复速度并提升稳态频率的幅值。

从参数灵敏度的大小来看,在扰动后频率响应的初期阶段,虚拟惯量系数为频率动态特性的主导影响因素,其大小的改变对频率动态过程的影响程度大于频率下垂系数。随着频率下降速度的减缓和下降幅值的增大,频率下垂系数逐渐成为主导影响因素。尤其当进入新的稳态阶段后,频率稳态特性只受频率下垂系数的影响。

3.3 参数调整效果验证

根据2.3节所提参数调整策略,基于表1所示仿真系统,计算频率最低点对虚拟惯量系数Ki和频率下垂系数Kd的区间轨迹灵敏度,结果如表2所示。

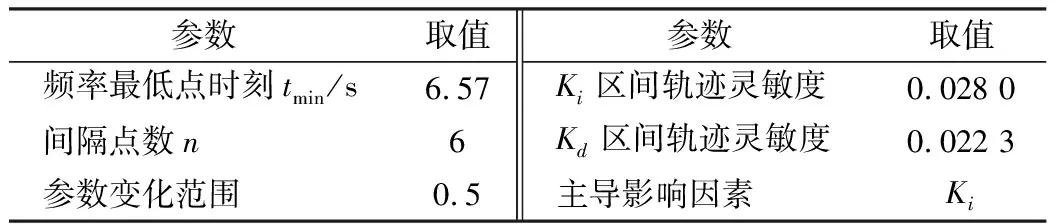
表2 频率协调控制参数的区间轨迹灵敏度

结果表明,Ki的区间轨迹灵敏度明显大于Kd,此时Ki为频率最低点的主导影响因素。以0.5作为参数Kd和Ki的变化量,对比两种参数变化方式下的频率动态特性,如图4所示。

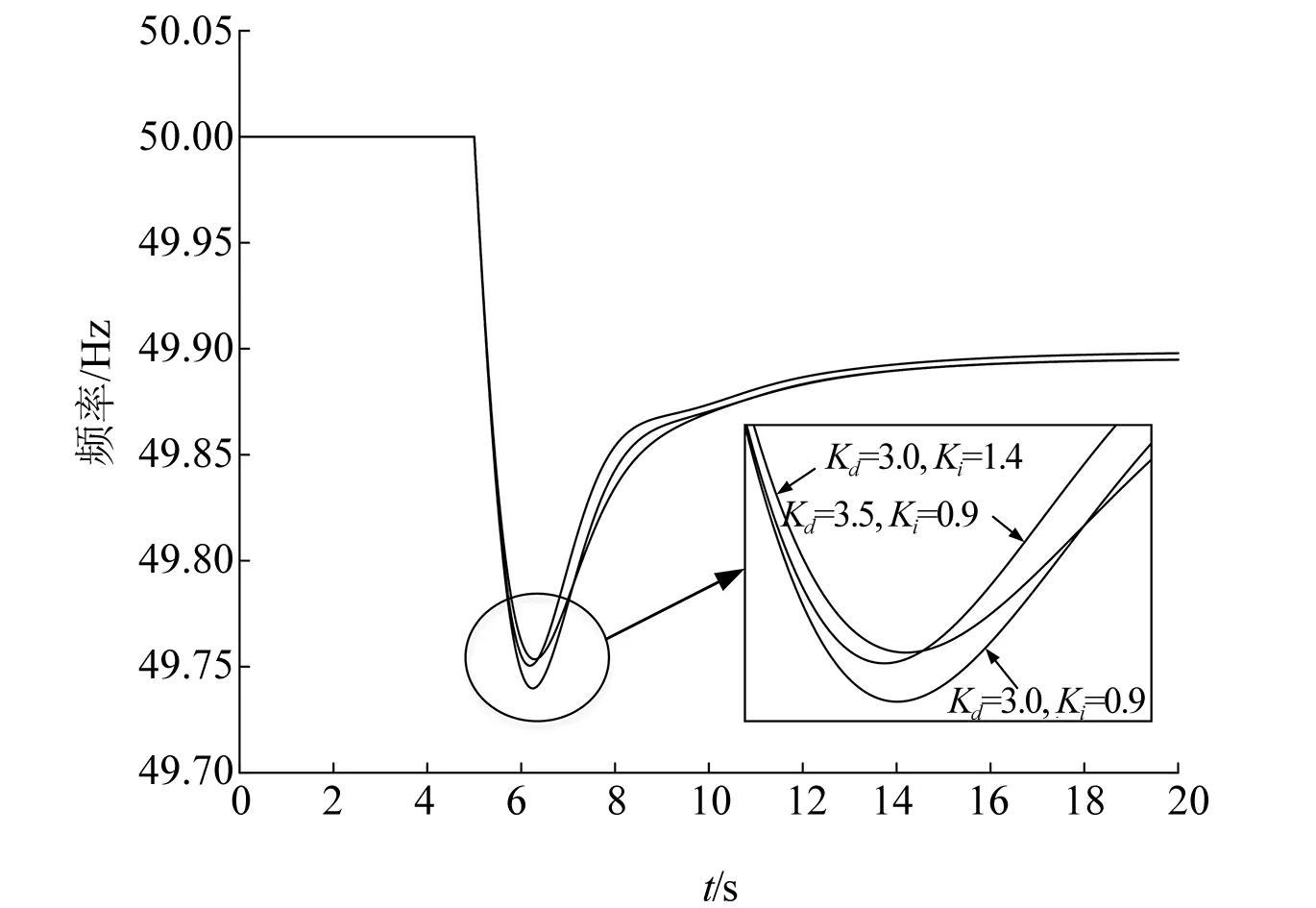
图4 控制参数变化下频率响应特性对比

可以看出,当参数变化相同大小时,调节虚拟惯量系数Ki对频率动态最低点的改善效果较调节频率下垂系数Kd更好,仿真结果与基于参数区间轨迹灵敏度的分析相一致,验证了所提参数调整策略的有效性。

4 结束语

本文研究了结合虚拟惯量控制和频率下垂控制的频率协调控制原理,基于轨迹灵敏度方法,从影响时间、影响方式和影响程度三个方面量化分析了控制参数对系统频率动态特性的影响。在此基础上,针对频率最低点提出了频率协调控制的参数调整策略,进一步提升了快速频率响应资源参与惯量支撑和一次调频的效果,对实际工程具有一定的指导意义,后续将围绕如何基于轨迹灵敏度方法对控制参数进行最优化计算开展进一步研究。