PDC钻头复合冲击钻进动力学研究

2023-10-12邓银江郭正伟魏秦文程泽正向荣洵

石油矿场机械 2023年5期

邓银江, 郭正伟, 魏秦文, 程泽正, 向荣洵

(1.重庆科技学院, 重庆 401331; 2.重庆青山工业有限责任公司, 重庆 402776)

随着浅地层油气资源的枯竭,油气勘探目标逐渐进入到深部地层。据最新勘探结果,国内深层、超深层油气资源达671亿 t油当量,占全国油气资源总量的34%;以塔里木盆地区为例,仅埋深6 000～10 000 m的石油和天然气资源就分别占其总量的83.2%和63.9%,超深层油气占全球资源总量的19%[1]。深地层油气资源储量丰富,但地层温度高、岩石硬度大、研磨性强,常规钻井方式出现进尺慢、钻头磨损快、憋跳严重等系列问题,造成深井油气资源得不到有效开发。PDC钻头传统破岩方式主要可以分为岩石变形、裂纹发生、切削核形成和块体崩裂4个阶段[2],如图1所示,由于深井中的岩石塑性较大,导致钻速降低,钻头寿命短。为提高深井硬岩地层的机械钻速,常采用复合冲击钻井技术,其实质是在常规钻井技术基础上附加冲击载荷,钻头在冲击载荷与旋转剪切力共同作用下破碎岩石。据文献调研发现,复合冲击钻井的机械钻速比常规钻井方式快2～3倍,在中等硬度花岗岩中其机械钻速甚至能够提高7倍以上[3],这对于深井油气资源的开发具有重要意义。

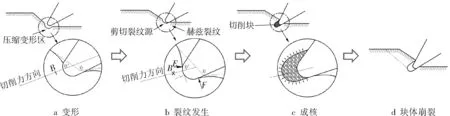
图1 PDC钻头传统破岩方式4个阶段

柳贡慧[4]等人研究了传统轴向冲击钻井和扭转冲击钻井钻头匹配性差和地层适应性差的问题,在2016年首次提出了复合冲击破岩钻井技术,并对复合冲击钻井工具的结构、工作原理、破岩效率影响因素等进行了研究,提出复合冲击钻进时岩石更容易产生体积破碎。Zichen Xu[5]等人提出一种复合冲击器,并完成了该工具设计参数下的数值模拟和试验验证,试验中该工具使平均机械钻速提高150%。闫炎[6]等人研究了复合冲击作用下PDC钻头破岩效果,进行了石灰岩、花岗岩和粉砂岩常规破岩与复合冲击破岩试验,研究了转速、钻压、冲击扭矩和冲击力对PDC钻头钻进速度影响规律,得出复合冲击破岩相比常规破岩能够产生更大粒径的岩屑,破岩效率更高,且冲击扭矩、冲击力与破岩效率呈正相关。彭旭[7]等人研制了复合冲击螺杆钻具,并对冲击螺杆的水力特性、复合冲击动力学特性进行研究,基于复合冲击破岩模型,得出轴向动载荷和轴向静载荷是影响破岩效果的主要因素。研究人员对复合冲击钻井技术的提速效果进行了大量研究,证明了复合冲击钻进技术能够有效提高硬岩地层钻进速度,但对于复合冲击钻进提速机理研究较少。

本文提出了一种轴扭复合冲击破岩工具,如图2所示。建立了PDC钻头钻进理论模型和数值计算模型,分析复合冲击工具配合PDC钻头的轴扭复合冲击破岩机理。如图2所示的轴扭复合冲击工具在泥浆压力驱动下,扭转摆锤周向往复运动并产生扭转冲击,轴向冲锤轴向往复运动并产生轴向冲击,这2种附加冲击载荷直接施加在PDC钻头后端,能够辅助PDC钻头高频切削岩石,进而提高钻进速度。

图2 轴扭复合冲击工具结构示意图

1 PDC钻头破岩模型

1.1 理论模型

在一定钻压下,PDC钻头常规破岩方式主要通过刮切方式破岩。取单颗齿为研究对象,设定切削深度为恒定常数,如图3所示。切削齿破岩过程可以分解为对岩石纯剪切破碎和沿着切削面摩擦2个过程[8],刀具所受的力为作用于切削面上的力Fc与作用于摩擦面上的力Ff的合力,稳定切削时Fc与Ff都可以视为常数,Fc与Ff可以沿刀具运动方向(s向)及运动垂直方向(n向)进行分解,如式(1)所示。

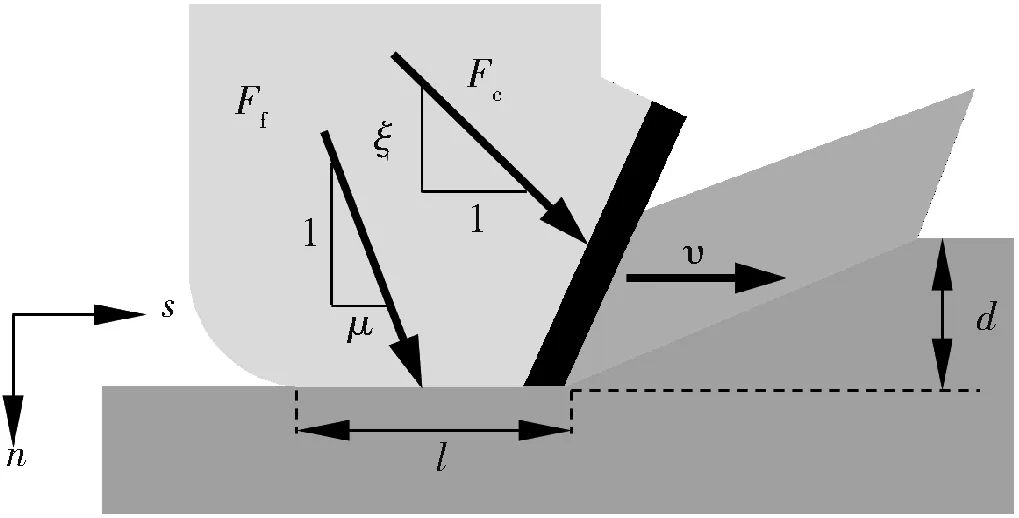
图3 PDC钻头切削齿破岩模型示意图

Fc=(Fcs,Fcn)T,Ff=(Ffs,Ffn)T

(1)

各分力可表示为:

Fcs=εwd,Fcn=ξFcs,Ffs=μFfn,Ffn=σwl

(2)

式中:ε为岩石破碎比能;wd为切削齿有效切削面积,m2;ξ为切削齿运动方向特征量;μ为钻头与岩石间的摩擦因数;σ为切削齿摩擦面与岩石接触面的最大接触压力,Pa;wl为切削齿摩擦接触面积,m2。

钻进过程中的钻柱系统可以简化为扭转摆动模型,如图4所示。

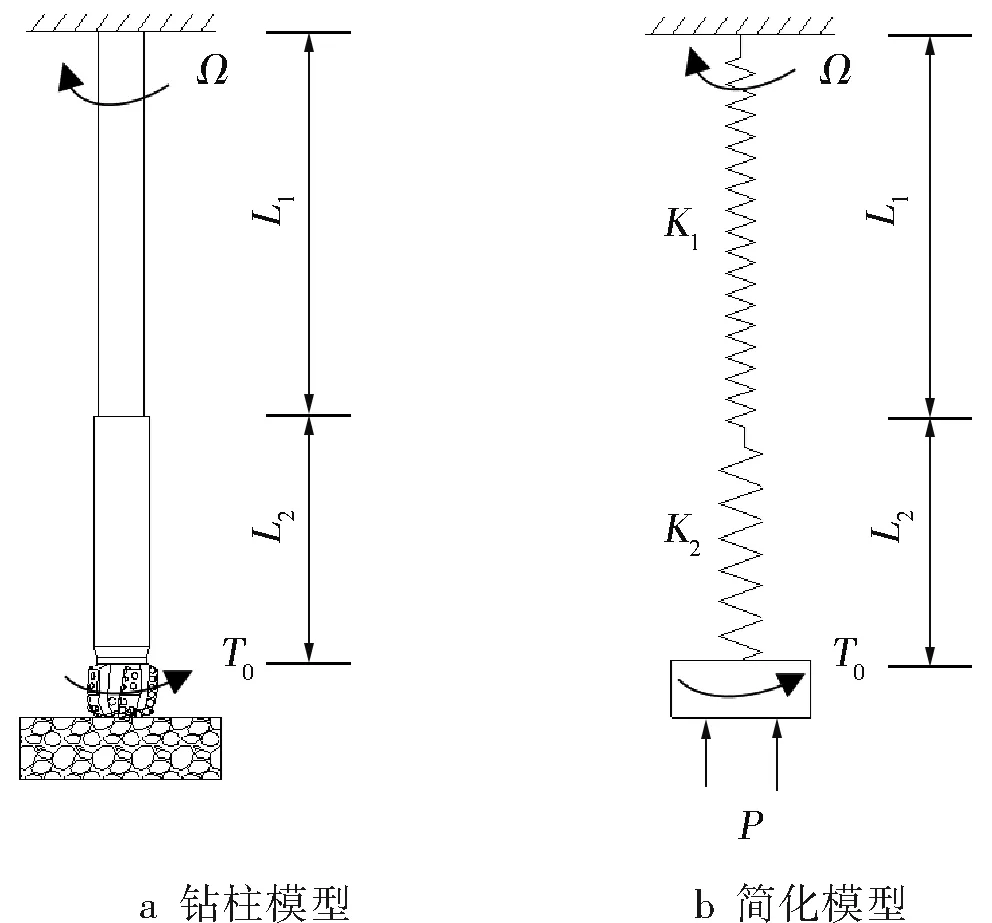
图4 PDC钻头钻进过程钻柱系统简化模型

图4中,Ω为转盘转速;L1、L2分别为钻柱系统钻杆、钻铤长度;K1、K2分别为钻柱系统钻杆、钻铤等效刚度;T0为粘滑振动过程中,钻头转动时受到的反转矩,转动过程中该值为常数;P为转动过程钻头受到的钻压。

对于钻头粘滑振动过程,其受到的反转矩可表示为:

(3)

式中:T为粘滑振动过程中,钻头转动时钻柱系统提供的切削转矩,N·m;T0+ΔT为钻进过程中,钻头受地层的最大反转矩,N·m;ΔT为粘滑振动过程中,钻头静止时所受反转矩与转动时所受反转矩的最大差值,N·m;θ为钻头旋转角度,rad。

当钻头处于粘滞状态时,钻柱系统可以等效为扭摆模型,故钻头运动方程可以表示[10]为:

(4)

式中:J为钻柱系统等效转动惯量,kg·m2;K为钻柱系统等效刚度,(N · m)/rad。

根据钻柱系统模型,钻柱系统等效转动惯量J及等效刚度K可以表示为:

J=ρI1L1+ρI2L2

(5)

(6)

式中:ρ为钻柱材料密度,kg/m3;I1、I2分别为钻柱系统中钻杆、钻铤的截面极惯性矩,m4;L1、L2分别为钻柱系统中钻杆、钻铤的长度,m;G为钻柱材料剪切模量,Pa。

其中,钻杆、钻铤的截面极惯性矩可表示为:

(7)

式中:D1、d1和D2、d2分别为钻杆的外径、内径和钻铤的外径、内径,m。

钻柱粘滑振动是周期性变化过程,假设在t=0时刻,钻头开始滑脱,此时钻柱提供给钻头的转矩一定大于钻头受到的岩石阻力,所以对于式(4)有如下初始条件。

(8)

由式(4)得出钻头在该初始条件下的运动方程为:

(9)

式中:ω0为钻柱系统角频率,rad/s;φ为相位角,rad。

(10)

(11)

对式(9)求导,得出钻头转速方程:

(12)

假设滑脱过程持续时间为t1,即有:

(13)

得出滑脱持续时间t1与钻柱系统参数之间的关系,以及t1时刻钻头角位移。

(14)

(15)

当摩擦力矩再次达到上限,钻头停止转动,此时可由周期性粘滑平衡求解粘滑周期Ts。

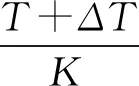
(16)

联合式(11)、式(14)、式(15)、式(16)得出该系统粘滑振动周期Ts。

(17)

得到常规钻井PDC钻头扭转振动动力学方程式:

(18)

复合冲击器主要是为钻头提供轴向和周向冲击载荷,改变钻头原有破岩方式。由于PDC 钻头传统破岩方式不存在轴向冲击,因此钻头轴向冲击频率等于复合冲击器的轴向冲击频率。但是,在周向由于钻头存在粘滑振动,复合冲击器的扭转振动会改变原有钻头的粘滑振动。

1.2 数值分析模型

PDC钻头破岩过程十分复杂,其运动轨迹受岩石属性、地层压力、钻柱长度及井底流场等因素影响。本文主要研究轴扭复合冲击破岩,对模型进行合理简化[9],做出以下基本假设:

1) 岩石为均质各向同性材料,不考虑岩石内部原始裂纹和孔隙压力的影响。

2) 忽略钻头磨损及变形,将钻头定义为刚体。

3) 忽略温度及井底流场对破岩过程的影响。

4) 岩石脱落后立刻消失,忽略岩屑二次破碎。

利用三维建模软件建立钻杆-钻头-岩石几何模型,钻头直径为φ240 mm(9in)。根据常用钻柱尺寸组合[10],取钻铤直径φ177.8 mm(7 in),钻杆直径φ127 mm(5 in)。为减小边界对岩石切削过程的影响,岩石直径取φ700 mm。PDC钻头破岩过程为瞬态过程,其网格质量会直接影响仿真结果,为节约计算成本,对钻头-岩石接触区域进行网格局部加密,得到PDC钻头破岩几何模型、网格模型如图5所示。

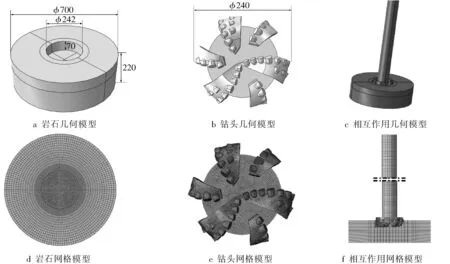
图5 钻头破岩分析模型

岩石本质上属于各向异性材料,其受到外部载荷作用会出现弹性、塑性变形和脆性断裂等力学行为,合理选择岩石本构模型对仿真结果至关重要。Drucker-Prager(D-P)准则能够较好地反映岩石材料特性,在仿真模拟中得到广泛应用[11-13],其屈服面可以为线性、双曲线和指数函数模型。本文采用线性D-P模型来定义岩石,其屈服面如图6所示。

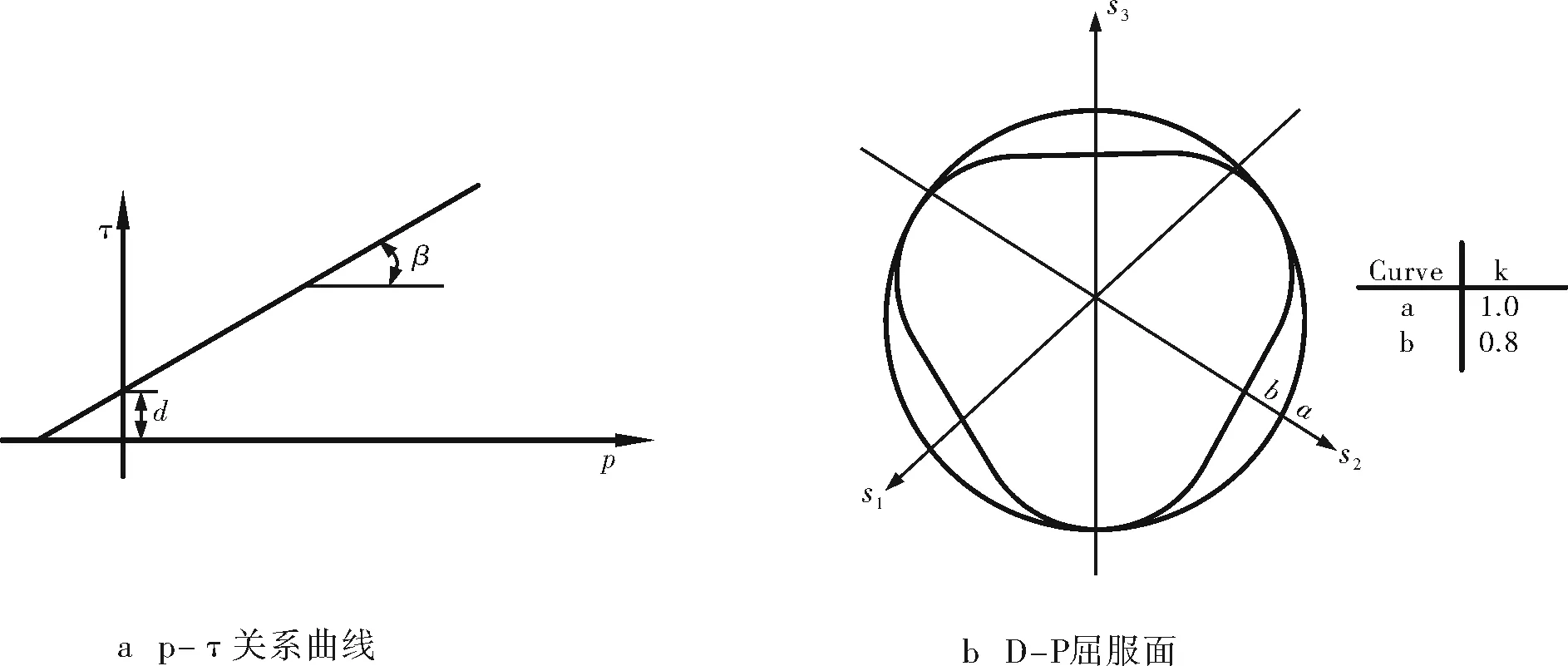
图6 线性Drucker-Prager模型屈服面

其屈服准则函数为:

F=τ-ptanβ-d=0

(19)

式中:p为等效压应力,MPa;β为屈服面应力空间倾角,(°);d为岩石粘聚力,MPa;τ为偏应力,MPa。

(20)

式中:q为等效Mises应力,MPa;k为流应力比;r为应力偏张量第三不变量,MPa。

为反映深井硬岩地层岩石特性,数值分析岩石模型采用花岗岩,其模型材料参数如表1所示。

钻头定义为刚体,不考虑破岩过程中的变形及磨损,其密度为7 850 kg/m3,根据几何模型得出钻头具体参数如表2所示。

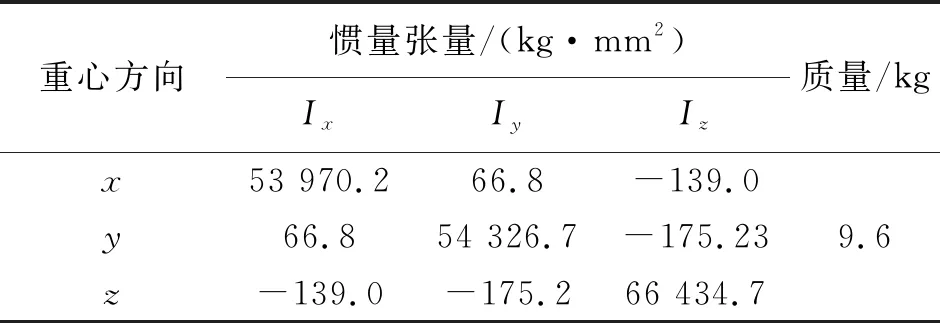
表2 钻头模型参数

注:x、y、z分别为PDC钻头重心矢量方向。

钻杆采用线弹性模型,材料为42CrMo(ISO 683/1 3),其具体参数如表3所示。

表3 钻杆模型材料参数

假设钻井井深2 000 m,岩石上覆地层压力为49 MPa,泥浆液柱压力为22 MPa,岩石围压为11.5 MPa。PDC钻头可用较低钻压钻进,根据克里斯顿金刚石复合片钻头钻压推荐表[15],本文所用钻头钻压取值为15～120 kN。由于模型中钻杆未设置周向约束,取较低钻压值20 kN,钻头转速为120 r/min。根据冲击载荷发生方式,施加载荷为正弦函数[16]。

模型边界条件施加如图7所示。

2 模型验证

本文采用理论模型与数值分析模型结果对比进行模型验证。首先采用数值分析模型计算20 kN钻压情况下,转盘转速31.4 rad/s时PDC钻头钻进情况。再将仿真模型参数代入理论模型进行计算,得出PDC钻头数值分析模型、理论模型转速情况如图8所示,因0～0.1 s仿真模型钻压、转速为匀速加载过程,故取0.1～1.0 s进行分析,其转速平均值误差为0.44%,能够满足工程误差要求。

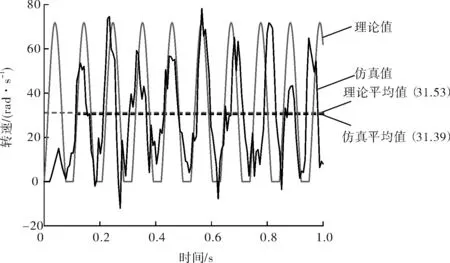
图8 PDC钻头理论、数值分析模型扭转振动对比

3 结果分析

PDC钻头切削过程运动轨迹,如图9所示,常规钻进时PDC钻头吃入岩石阶段周向摆动较大,吃入一定深度后在钻头定心作用下,周向摆动明显下降,钻压作用下钻头轴向进尺较为均匀;复合冲击作用下,钻头整个切削过程较为均匀,轨迹呈螺旋趋势。对比钻进过程钻头轴向进尺,复合冲击钻进相比常规钻进机械钻速明显提高。

图9 PDC钻头不同钻进条件下钻进轨迹

PDC钻头钻进过程中钻杆最大应力(Mises)如图10所示(钻进过程中钻杆发生扭转变形,钻头转角相对于转盘滞后一定角度,为便于分析,取转盘转动角度作为坐标轴),常规钻进时由于PDC钻头吃入深度较小,其钻杆应力变化较为平滑。复合冲击作用下PDC钻头单次进尺大,岩石切削反力大,但在扭转冲击作用下PDC钻头能够快速破碎岩石,使钻杆应力呈波动状态。

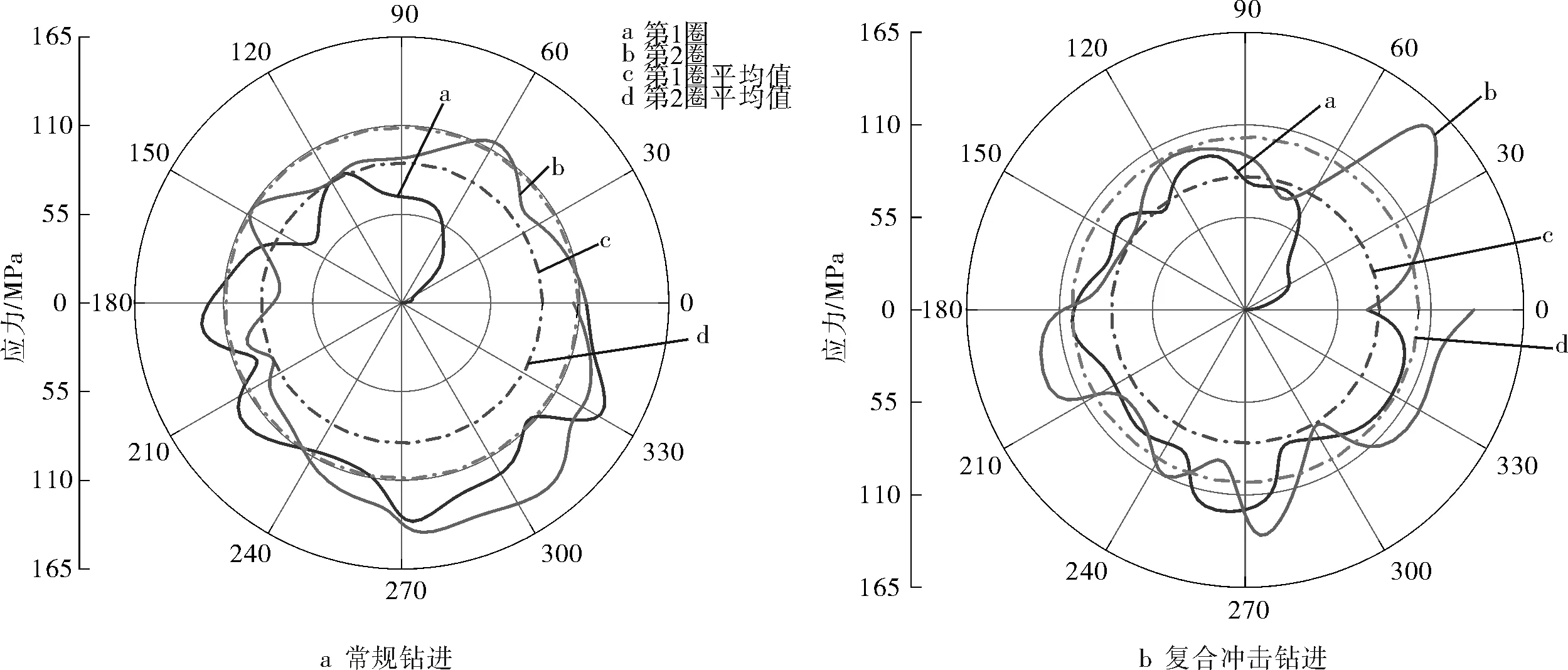
图10 PDC钻头钻进过程钻杆最大应力情况

提取岩石圆周节点处(路径位置如图11所示),常规钻进和复合冲击钻进岩石破碎过程最大主应力值(拉应力为正,压应力为负),PDC钻头破岩过程为圆周运动,不同时刻圆周节点最大主应力分布如图12所示。

图12 不同时刻岩石节点处最大主应力分布图

由图12可知:

1) 0.1 s时。岩石处于变形阶段,此时岩石所受最大主应力基本为负值,即主要受压应力,发生弹性变形。在常规钻进和复合冲击钻进作用下,圆周路径上岩石单元应力分布大致相同。由于复合冲击钻进存在轴向和扭转冲击载荷,其应力波动略大于常规钻进。

2) 0.2～0.3 s时。岩石处于裂纹发生阶段,该过程中岩石单元所受应力出现大量正值,即岩石所受应力大多为拉应力。复合冲击钻进过程中拉应力圆周分布更加密集,且应力幅值较大,其原因为复合冲击钻进过程中,PDC钻头在钻压、转速作用下,额外受到轴向和扭转冲击作用,辅助载荷作用下PDC钻头更容易吃入岩石地层形成有效切削。

3) 0.4 s时。复合冲击作用下岩石已经开始破碎,出现较小的破碎坑,部分区域已形成稳定切削,应力波动明显降低,此时常规钻进还处于裂纹发生阶段,应力波动较大。

4) 0.5 s时。复合冲击作用下,岩石已经形成较大的连续破碎,此时常规钻进才刚开始出现破碎坑。

5) 0.6 s时。复合冲击作用下,岩石已经发生大量破碎,仅有个别网格未发生破坏,此时常规钻进才刚开始出现较小的零散破碎坑。

6) 0.7 s时。复合冲击作用下,岩石已经完全破碎,而常规钻进直至1 s时才完全破碎。

通过对比分析可以得出,复合冲击作用下岩石裂纹发生快,且更容易产生体积破碎,钻进时间相对于常规钻进可提速30%左右,岩石表面能够形成连续均匀的破碎坑,故复合冲击钻进机械钻速高于常规钻进,且能够形成平整的井底形态。