基于智能变后缘的超微型无人机高度控制研究

杜昊炜，刘 振，康子晗，李世琪

（西安交通大学航天航空学院，西安 710049）

1 引 言

微型无人直升机具备体积小、灵活、低成本和安全可靠的特点，可以在多种环境下完成任务，在军用、民用方面受到广泛欢迎［1-2］。相应地，如何对微型飞行器在低雷诺数下进行有效的控制也成为了当前研究的重点［3］。研究表明［4-5］，通过在旋翼后缘安装襟翼可以有效改善飞行器气动特性。传统的离散式后缘襟翼通过机械结构驱动后缘偏转，可以有效提升旋翼的悬停效率［6］。离散式后缘襟翼主要包括格尼襟翼［7-8］、自适应襟翼［9-10］、多片后缘小翼［3］等，但由于离散式后缘襟翼涉及较为复杂的机械结构并且自身质量较大，往往不适合用于微型旋翼上。近年来学者提出连续后缘襟翼（Continuous Trailing-Edge Flap，CTEF）的概念，对柔性材料施加外部激励，使其实现连续变形。Shen［11-12］等以压电纤维复合材料作为驱动材料，基于VR-18翼型设计了CTEF，用于直升机主旋翼飞行控制；美国国家航空航天局兰利研究中心［13］基于NACA0015 翼型设计了CTEF。实验结果表明，采用CTEF会使得翼型具有更高的升力系数及更高的升阻比，因此CTEF十分适合应用在微型旋翼上。

由于连续后缘襟翼可以有效改变桨叶气动特性，并且具有质量较小，不涉及复杂的机械结构等优点，同时目前国内外针对微型旋翼的连续后缘襟翼方面的研究比较少，因此本文将连续后缘襟翼应用于微型旋翼飞行器上，使用智能材料建立一个带有连续后缘襟翼的微型旋翼模型，同时实现其有效控制，最终实现垂直升降功能，并通过数值仿真研究该种襟翼对于微型桨叶推进性能的提升效果。本文研究内容包括：

（1）微型桨叶推进特性研究。建立微型桨叶的气动仿真模型，计算旋翼转速为6000 rpm 时，不同攻角下旋翼的气动系数。并利用拉力系数、品质因数等判断依据确定典型安装角，在此基础上建立连续后缘襟翼的气动仿真模型。

（2）基于P（VDF-TrFE）的连续后缘襟翼设计。在典型攻角下，选取桨叶材料，设计带有连续后缘襟翼的桨叶结构，通过仿真实现后缘变形。在此结构的基础上，通过对后缘襟翼施加不同的电压，利用单向流固耦合的方法研究后缘襟翼偏转对旋翼推进性能的影响，并建立电压与气动升力之间的拟合关系。

（3） 基于比例、积分、微分（Proportional Intergral Derivative，PID）控制器的无人机高度控制系统设计。在第三章中建立的电压与旋翼拉力之间拟合关系的基础上，利用PID 控制器，设计微型无人机高度控制系统，从而实现微型桨叶的智能控制，使这种带有连续后缘襟翼的微型旋翼可以带动无人机实现高度控制。

2 微型旋翼推进特性研究

2.1 微型旋翼流场模拟

如图1所示，本文使用的微型旋翼模型由一对展长32.5 mm，弦长14.8 mm，厚度0.3 mm 的微型桨叶组成。以该模型为基础，使用滑移网格法绘制结构体网格。考虑到旋翼下游存在尾迹区与叶尖涡等复杂流场，选择圆台形作为微型旋翼的流场计算区域。如图2 所示，将整个流场区域分为两个部分，内部是包含旋翼的旋转区域，为运动部分；外部是包含运动部分的区域，为静止区域，两部分的几何尺寸如表1、表2所示。

图1 微型旋翼模型Fig.1 Micro rotor model

图2 流场结构划分Fig.2 Flow field structure division

表1 旋转区域几何参数Table 1 Geometric parameters of the rotation region

表2 静止区域几何参数Table 2 Geometric parameters of the rest region

本文采用结构化网格划分旋翼流场，因为其具有网格质量高、计算速度快等优点。本文主要采用了O 型拓扑结构的网格，其目的是减小流场上、下表面网格扭曲程度。图3、图4 分别为内、外流场的区域拓扑划分，在内流场和旋翼内部划分O 型网格拓扑结构。由于旋翼结构较为简单，故沿旋翼展向没有进行过多的划分。但由于旋翼弯度较大，为了更好地拟合旋翼几何形状，沿旋翼弦向进行了多次划分。

图3 内流场拓扑划分Fig.3 Topological division of internal flow field

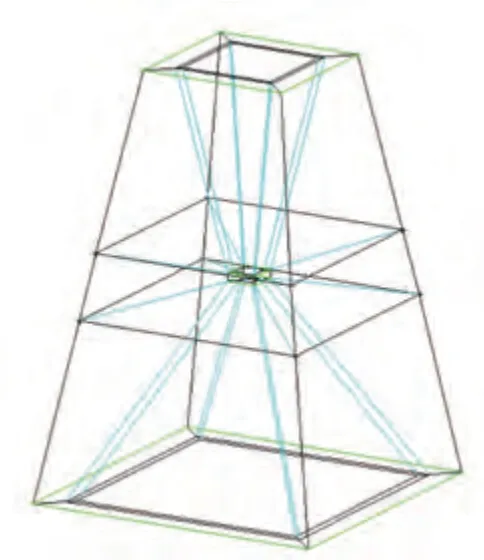
图4 外流场拓扑划分Fig.4 Topological division of outflow field

在网格拓扑结构划分的基础上，进行网格节点布置，进而完成网格绘制。在绘制过程中，考虑到旋翼翼尖处存在翼尖涡等现象，流场较为复杂；翼根处转速较低，但由于尾迹区的存在，流场情况也较为复杂；前缘为迎风面，压力梯度较大；后缘压力梯度较小，但存在涡脱落等现象。因此为了更好地模拟流场特性，在上述部位分别进行了网格加密，加密后旋翼表面网格如图5 所示。由于旋翼旋转时的雷诺数较小，黏性效应较为显著，故需对旋翼壁面附近的边界层处的网格加密。根据Y+原则，由于湍流模型选取Laminar模型，通常令Y+的值为1.0。图6 为边界层网格，当 Y+的值为1.0 时，靠近旋翼壁面第一层网格厚度为0.02 mm。整体网格图如图7所示，内流场网格数量110 万，外流场网格数量50 万，网格质量在0.6以上。

图5 旋翼表面网格Fig.5 Rotor surface mesh

图6 边界层网格Fig.6 Boundary layer grid

图7 整体网格图Fig.7 Overall grid diagram

针对旋翼悬停状态进行流场模拟，开展旋翼推进特性研究。

（1）求解方式

采用压力基求解器，差值格式为coupled 算法，以二阶迎风作为求解精度。

（2）湍流模型

采用Laminar模型进行稳态求解。

（3）流体属性

空气密度为1.1241 kg/m3， 粘性系数为1.8489e-5kg/（m·s），均由测量当地空气系数得出。

（4）边界条件

速度入口：外流场上表面与圆台的周面，入口速度为0.002 m/s，沿Z轴负方向。

压力出口：外流场下表面，以大气压强作为静压。

动区域：旋翼绕Z轴负方向旋转，转速6000 RPM。

交界面：旋转的旋翼区域与外部静止区域通过交界面进行连接。

2.2 数值模拟结果分析

在12°～30°范围内改变桨叶安装角，得到一系列不同安装角下的微型旋翼模型，以2.1 章节中的网格绘制方法为基础绘制一系列不同安装角下的旋翼流场网格，通过Fluent 计算出不同安装角对应的旋翼拉力以及扭矩，如表3所示。

表3 不同安装角旋翼的拉力及扭矩Table 3 Tension and torque of rotors with different installation angles

由表3 可以得到旋翼拉力与安装角的关系，如图8 所示。可以看出安装角范围在12°～30°时，旋翼没有明显的拉力损失。为了更好地分析仿真结果，将拉力、扭矩无量纲化，定义拉力系数、功率系数、品质因数，其中品质因数Qf是理想旋翼诱导功率Pi与旋翼功率P的比值，表征了旋翼的悬停效能［14］。旋翼的拉力系数CT为

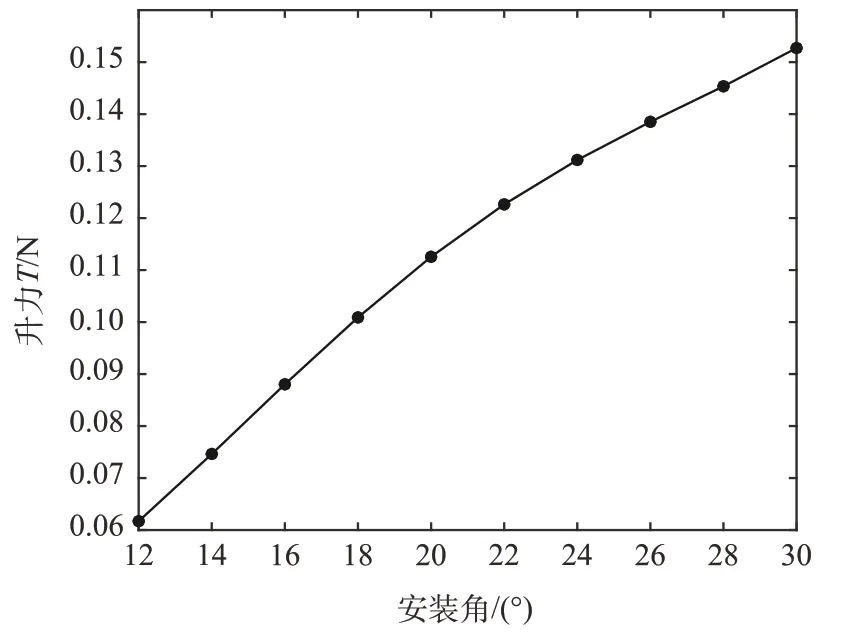
图8 拉力随安装角的变化Fig.8 Lift varies with installation angle

其中，T为旋翼拉力，ρ为流体密度，A为旋翼桨盘面积，R为旋翼半径，Ω为旋翼旋转速度。功率系数CP为

其中，Q为旋翼扭矩。品质因数Qf为

由上述三式可以得到品质因数Qf与安装角的关系。如图9 所示，品质因数Qf最大值在旋翼安装角为18°时出现，表明采用这一安装角时，旋翼工作效率较高。因此选取18°为典型安装角，以安装角为18°的旋翼为基础设计CTEF。

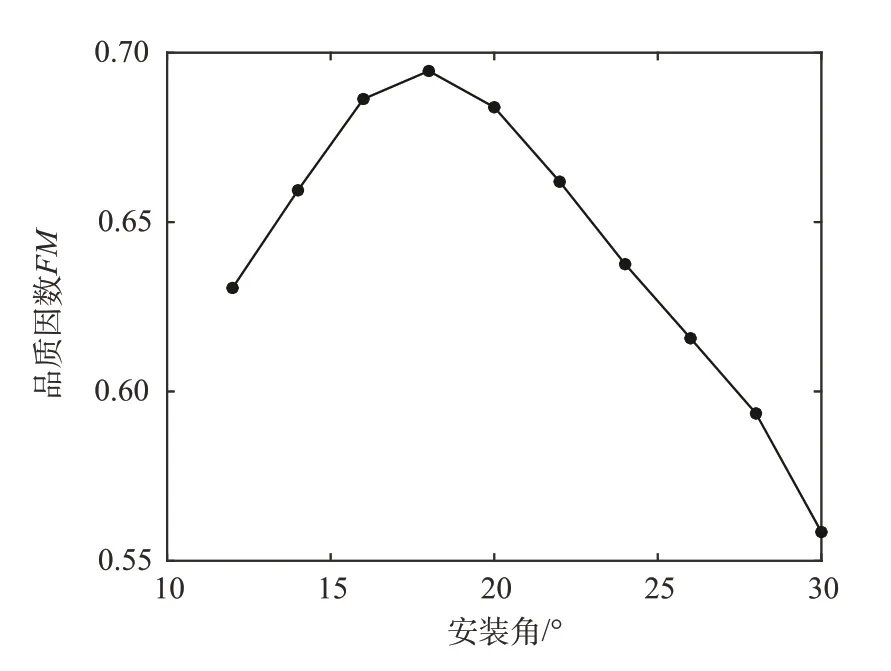
图9 品质因数随安装角的变化Fig.9 The quality factor varies with the installation angle

3 基于P（VDF-TrFE）的CTEF设计

3.1 P(VDF-TrFE)材料本构关系

利用聚偏氟乙烯共聚物［P（VDF-TrFE）］可以制成一种柔软、质轻、高韧度的薄膜，它在电压驱动下可以发生较大的变形。本文使用的P（VDF-TrFE）材料来自Zhang［15］等的研究成果，利用通过原子层沉积生长的新型核壳结构的CNTAl2O3纳米颗粒来改善P（VDF-TrFE）的机电性能。添加1.1 wt%的CNT-Al2O3纳米复合材料的横向诱导应变比规整的P（VDF-TrFE）提高600 %。在相同的诱导应变下，纳米复合材料所需的驱动电压可有效降低高达200 %。P（VDF-TrFE）的性能参数如图10～11 所示。后文中的P（VDF-TrFE）材料均特指添加1.1 wt%的CNT-Al2O3的P（VDFTrFE）材料。由P（VDF-TrFE）驱动的后缘襟翼可以发生连续变形，达到改变旋翼推进特性的目的。因此准确计算P（VDF-TrFE）材料在电场作用下的变形十分重要。

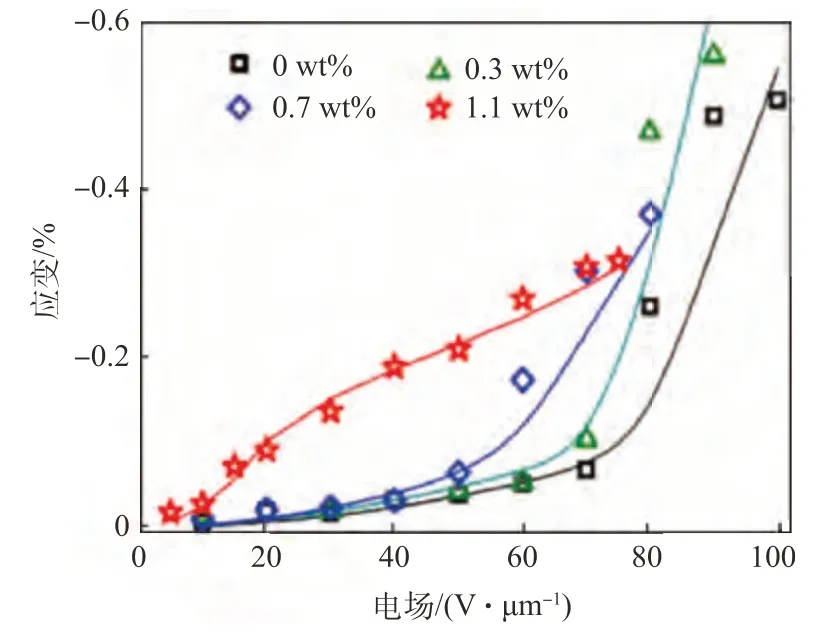
图10 应变-电场关系[15]Fig.10 Strain-electric field relationship[15]

在外加电场作用下，P（VDF-TrFE）材料产生的应变由电致伸缩应变和麦克斯韦应变组成［15］

式中，St是外加电场方向上的总应变，SM是麦克斯韦力引起的应变，SE是电致伸缩效应引起的应变，Y是材料的杨氏模量，ε0是真空介电常数，εr是材料的相对介电常数，E是外加电场的电场强度，Q是材料的电致伸缩系数，P是电场强度为E时材料的极化强度，μ是材料泊松比。

当压电晶体受到外力而发生形变时，在它的表面上出现与外力成线性比例的电荷积累，这个现象称为压电效应［16］。本文将P（VDF-TrFE）材料的电致伸缩效应和麦克斯韦应力等效为压电效应进行仿真模拟。压电效应的应变表达式为

式中，T是应力向量，D是电位移向量，S是弹性应变向量，sE是电场强度恒定时的弹性矩阵，d是压电应变矩阵，εT是机械应变恒定时的介电常数矩阵，E是电场强度向量。

由于式（4）与式（7）构造形式相似，故可以将P（VDF-TrFE）材料由于电致伸缩效应和麦克斯韦力引起的应变等效为由压电效应引起的应变。当材料在Z 轴方向上存在处处相等的电场时，式（4）可被表示为

式中，d33即压电常数，表示在Z轴方向上施加单位电场强度，材料在Z轴方向上发生的应变。由应变和材料泊松比可进一步得出，

式中，d31和d32分别表示在Z轴方向施加单位电场后，材料沿X轴、Y轴方向发生的应变。

由于电致伸缩效应和麦克斯韦应力不产生剪切力，故压电应变矩阵的其他项均为0。压电应变矩阵D可被表示为

利用式（11），即可模拟材料本构关系，进而在有限元软件中进行P（VDF-TrFE）材料的模拟仿真。

3.2 P(VDF-TrFE)材料仿真模拟

通过在有限元软件中对P（VDF-TrFE）材料进行仿真模拟，作为后续设计连续后缘襟翼的基础。由于P（VDF-TrFE）材料受到电场作用时发生形变，造成翼型弯度变化，进而改变旋翼拉力，故对所使用的P（VDF-TrFE）材料进行准确的仿真模拟十分重要。P（VDF-TrFE）材料的应变-电场关系如图10 所示。模拟仿真的目的是利用式（11），计算出在不同电场作用下材料的应变，将其与图10 进行对比，观察两者之间的匹配程度，若两者比较接近，则可近似认为模拟的P（VDFTrFE）材料与实际的P（VDF-TrFE）材料力学性能相同。

为了实现这一目的，需要获得任意电场强度所对应的极化强度，利用式（9）与式（10）计算出相应的压电系数，得到模拟材料的压电应变矩阵D。因此需要准确拟合出材料的极化强度-电场关系。使用Getdata 软件，从图11中的曲线上提取了若干个数据点所对应的数据，如表4 所示。以表4 中的数据为基础，用matlab 软件进行数据拟合，即可得到极化强度-电场表达式。

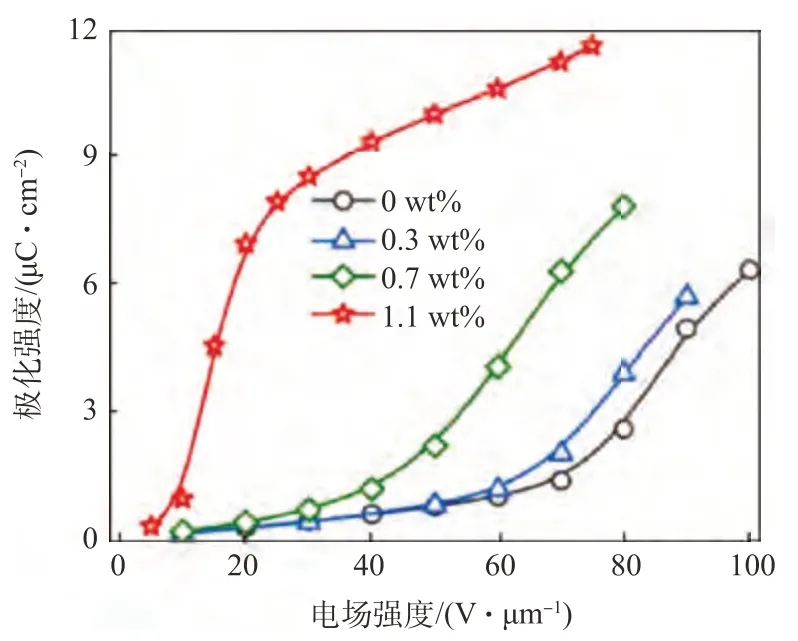
图11 极化强度-电场关系[15]Fig.11 Polarization intensity-electric field relationship[15]

表4 电场强度对应的极化强度Table 4 The electric field strength corresponds to the polarization strength

将表4中的数据进行高斯拟合，得到电场强度E与极化强度P的关系式为

式中，a1=10.38；b1=79.04；c1=18.42；a2=8.381；b2=52.33；c2=17.62；a3=6.28；b3=30.83；c3=13.81；a4=2.766；b4=20.82；c4=6.791；a5=1.329；b5=15.07；c5=4.037。

电场强度与极化强度关系如图12 所示。将拟合关系与添加1.1 wt%的CNT-Al2O3的P（VDFTrFE）材料的极化强度-电场强度关系进行对比，如图13 所示。发现在电场强度小于75 V/µm 的范围内，拟合的极化强度-电场强度关系与实际极化强度-电场强度关系基本一致。从图12 可以看出，电场强度大于75 V/µm 时，拟合曲线出现了下降的趋势，但由于对实际材料进行测试时，作用在材料上的最大电场即为75 V/µm，当电场强度继续增加时，材料会出现击穿现象。故电场强度大于75 V/µm 时材料的极化强度不具有过高的研究价值。因此，可以认为曲线拟合结果与试验测量结果基本一致。

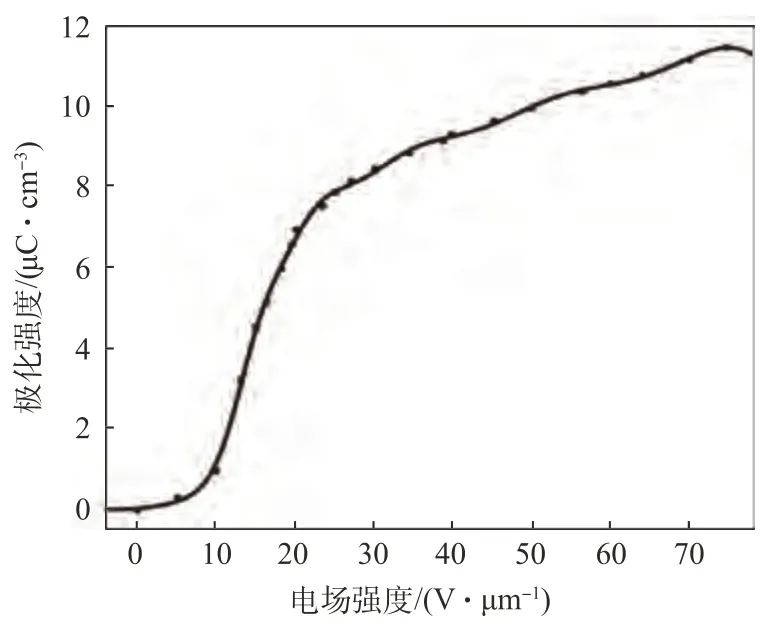
图12 极化强度-电场强度拟合关系Fig.12 Fitting relationship between polarization intensity and electric field intensity

图13 极化强度-电场强度对比Fig.13 Comparison of polarization intensity and electric field intensity

得出材料的电场强度-极化强度关系后，需要计算在不同电场下材料的应变，并将其与图10 进行对比，若相似度较高即可认为模拟材料与实际材料相同。由式（9）与式（12）可以计算得出任意电场强度所对应的压电系数d33，又由式（10）与式（11）可以得出相应电场强度下材料的压电系数矩阵D。本文通过上述方法计算得出的压电系数如表5所示。

表5 P(VDF-TrFE)模拟材料压电系数Table 5 P(VDF-TrFE) to simulate the piezoelectric coefficient of the material

通过表4中的数据计算模拟材料作用于不同电场下的应变。在Ansys 软件中建立一个几何模型，本文采用的模型为一个半径10 mm，高25 µm的圆柱形薄片，其表面网格绘制如图14 所示，通过不断改变薄片上、下表面电压，从而改变薄片内部沿Z轴方向的电场强度。结合表5中的数据，即可计算出材料在不同电场下的应变，如表6所示。

图14 仿真模型网格划分Fig.14 Simulation model meshing

表6 P(VDF-TrFE)模拟材料应变Table 6 P(VDF-TrFE) to simulate the piezoelectric coefficient of the material

由表6中的数据，可以得到模拟材料应变与电场强度之间的关系，如图15所示。在图16中，将拟合关系与添加1.1 wt%的CNT-Al2O3的P（VDFTrFE）材料的应变-电场强度关系进行对比，可以看出拟合的应变-电场强度关系与实际应变-电场强度关系基本一致，因此可以认为模拟材料能够在有限元软件中表征实际材料的力学性能。

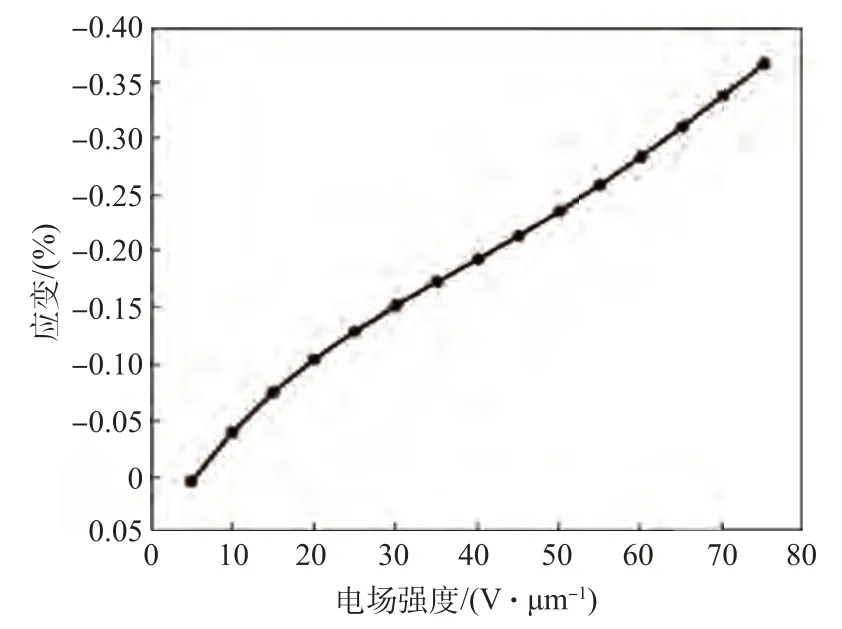
图15 应变-电场强度拟合关系Fig.15 Strain-electric field strength fitting relationship

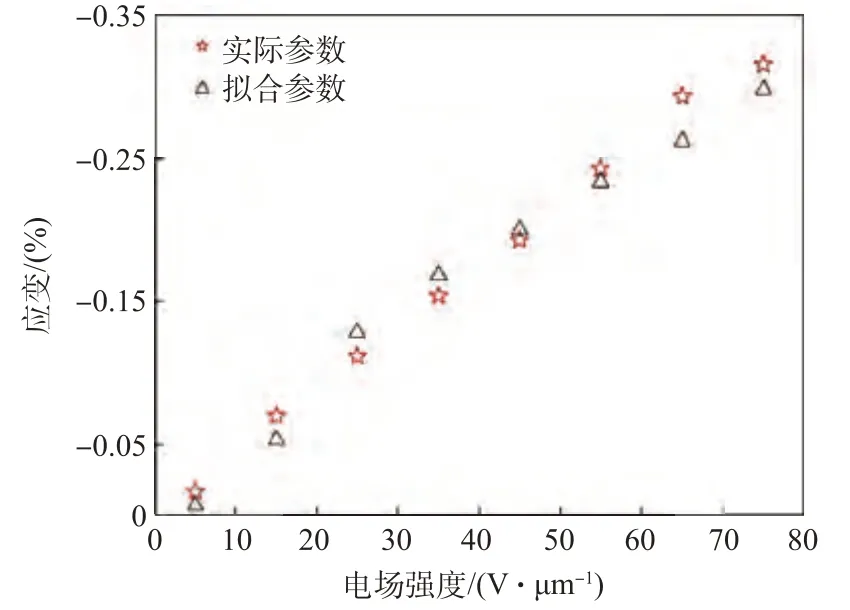
图16 应变-电场强度对比Fig.16 Strain - electric field intensity comparison

3.3 CTEF仿真模拟

设计带有CTEF 的微型桨叶结构，利用P（VDF-TrFE）材料制作后缘襟翼，对后缘襟翼施加电压即可实现变形［17］。桨叶结构如图17 所示，区别于常规的后缘襟翼，连续后缘襟翼与桨叶本身形成一个整体，通过电压驱动压电材料变形，实现襟翼偏转。桨叶弦长14.8 mm，厚度0.3 mm。桨叶基体用碳纤维材料制作，襟翼选用P（VDFTrFE）膜，从0.5 倍弦长处开始，沿桨叶中弧线延伸到桨叶后缘。由于碳纤维材料强度较大，变形能力较弱，若在其表面布置P（VDF-TrFE）膜，会限制P（VDF-TrFE）膜的变形。故选用变形能力较强的柔性材料作为基底，在其表面布置P（VDF-TrFE）膜，柔性材料与P（VDF-TrFE）膜之间铺设一层复合材料，固定P（VDF-TrFE）膜的下表面。在P（VDF-TrFE）膜上、下表面施加电压，膜内部出现沿厚度方向的电场。根据式（9）及式（10）可知，此时P（VDF-TrFE）膜会沿弦向、展向、厚度三个方向产生形变，由于P（VDF-TrFE）膜下表面固定在复合材料层上，产生变形较小，当P（VDF-TrFE）膜的上表面沿弦向产生形变时，桨叶弯度发生改变，进而实现了改变旋翼拉力的目的。

图17 桨叶弦向结构Fig.17 Chord structure of blade

聚二甲基硅氧烷（Polydimethylsiloxane，PDMS）材料是一种高分子聚合物，这一材料主要应用于硅芯片中，将其与硅基体相结合，提高整体结构的可变形能力，从而使电子器件在保持高性能的同时提高其延展性和韧性［18］。本文选用这一材料作为柔性材料基底，从而提高后缘襟翼的变形能力。桨叶基体选用碳纤维材料，P（VDF-TrFE）与PDMS 性能参数如表7所示。碳纤维是各向异性材料，其性能参数如表8所示。

表7 P(VDF-TrFE)与PDMS性能参数Table 7 P(VDF-TrFE) and PDMS performance parameters

表8 碳纤维性能参数Table 8 Performance parameters of carbon fiber

3.4 连续后缘襟翼流固耦合分析

弹性固体在流体载荷作用下发生变形，固体变形又会对周围流体分布产生影响，为了解决这一问题，本文采用了流固耦合仿真的分析方法。根据流固耦合机理的不同，流固耦合分析可被分为两大类［19］：

第一类耦合的特征是流固耦合仅发生在结构与流体的交界面上，物理量间的关系由两相耦合面上的平衡关系所确立，比较典型的实例有气动弹性、水动弹性等。

第二类耦合比较复杂，其特征是结构与流体之间存在部分或完全重叠，无法单独分开。使得需要针对特定的物理现象来单独构造本构方程之类的物理方程，通过微分方程来进行求解。

本文针对微型旋翼开展的流固耦合分析属于第一类耦合。流固耦合仿真分为单向流固耦合和双向流固耦合两种方法，考虑到双向流固耦合虽然计算结果较为精确，但计算效率较低，计算资源耗费大，对计算机性能要求较高，因此本文采用单向流固耦合的方法。工作流程如图18 所示，首先建立一个带有连续后缘襟翼的微型旋翼模型，在后缘襟翼表面施加电压，得到电场作用下发生变形的旋翼模型，对这一模型进行网格绘制、流场计算，得到模型表面的气动载荷分布，将气动载荷以及旋翼旋转时的离心力施加在旋翼表面，得到受气动载荷和离心力作用而发生变形的旋翼模型，对这一模型进行网格绘制、流场计算，并对旋翼进行流场分析及推进性能分析。

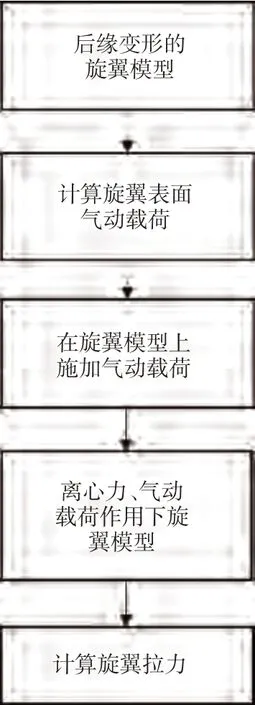
图18 单向流固耦合工作流程Fig.18 Unidirectional fluid-structure coupling workflow

下面以在电场强度为75 V/µm 作用下的微型桨叶为例介绍单向流固耦合的过程。首先进行模型的静态驱动仿真。静态驱动仿真是指在没有气动载荷的条件下，研究驱动电压对连续后缘襟翼的变形影响［20］。如图19、图20所示，桨叶基体部分固定，在PVDF膜的上、下表面施加电压，襟翼内部会出现沿厚度方向的电场。受到电场作用，微型桨叶后缘发生变形。以这一模型为基础在ICEM 软件中绘制网格，网格绘制过程与第二节中介绍的方法相同。

图19 变形前的微型旋翼Fig.19 Miniature rotors before deformation

图20 电场作用下的微型旋翼Fig.20 Miniature rotors with an electric field

依照第二节中的Fluent 参数设置方法，在Fluent 中进行流场计算，得到旋翼表面的气动载荷，将气动载荷与离心力施加在受电场作用而发生变形的旋翼模型上，得到离心力、气动载荷作用下的旋翼模型如图21 所示。对比图20 与图21，可以看出由于气动载荷和离心力的作用，后缘襟翼的变形效果受到了一定的影响。后缘整体位移有所下降，叶尖处受到的影响尤为显著，这一效果最终会导致后缘襟翼对旋翼拉力的控制能力有所下降，因此需要考虑气动载荷与离心力对旋翼气动性能的影响。对图21 中的模型进行网格绘制，在Fluent 中进行流场计算，可以得到该模型的拉力、力矩等气动参数，并对其进行流场分析与推进性能分析。

图21 离心力、气动载荷、电场作用下的旋翼Fig.21 Rotor under centrifugal force, aerodynamic load,electric field

3.5 推进性能分析

改变作用于桨叶上的电场强度，获得一系列变形程度不同的旋翼模型，按照第二节中介绍的网格绘制方法以及Fluent参数设置，在Fluent中进行流场计算，得到相应电场强度下的微型旋翼拉力（如表9 所示）以及旋翼扭矩（如表10 所示）。从表9 中的数据可以看出，当电场强度为75 V/µm时，旋翼拉力为13.29 e-2N，与未加电场时相比，拉力提高了约40%。由于桨叶变形时弯度发生改变，因此本文以等效安装角的方式表征桨叶的变形能力。将表3 中的数据在Matlab 中进行数据拟合，可以得到未安装连续后缘襟翼时，旋翼拉力f与安装角A之间的关系

表9 不同电场作用下的旋翼拉力Table 9 Rotor tension under different electric fields

表10 不同电场作用下的旋翼扭矩Table 10 Rotor torque under different electric fields

式中，p1=1.637e4，p2=-4480，p3=562.9，p4=-9.665。通过式（13），可以得到未安装连续后缘襟翼时，任意旋翼拉力所对应的旋翼安装角。将表9 中不同电场下的旋翼拉力代入式（13），即可得到后缘襟翼偏转产生的等效安装角，如表11 所示。从表11 可以看出，后缘襟翼偏转产生的最大拉力相当于旋翼安装角为24.44°时产生的拉力，因此后缘襟翼所产生的最大等效安装角为24.44°。

表11 后缘襟翼偏转产生的等效安装角Table 11 Equivalent mounting angle produced by deflection of trailing edge flaps

3.6 仿真结果分析

根据表9中的数据，即可得到旋翼拉力与电场强度之间的关系，如图22 所示，对其进行数据拟合即可得到旋翼拉力与电场强度的拟合关系，

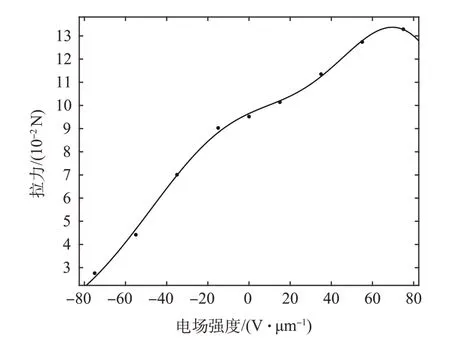
图22 电场强度与旋翼拉力关系Fig.22 Relationship between electric field strength and lift

式中，a1=11.27，b1=79.28，c1=48.81，a2=8.863，b2=-2.905，c2=64.9。利用式（14），即可设计飞行器高度控制系统，通过控制施加在后缘襟翼表面的电压实现无人机高度的控制。

4 基于PID控制器的无人机高度控系统设计

如图23 所示，本文以一种微型共轴双旋翼无人机作为物理模型，整机质量为10 g。共轴双旋翼飞行器有以下优点［21］：

图23 微型共轴双旋翼无人机Fig.23 Miniature coaxial twin-rotor UAV

（1）布局紧凑，纵向尺寸小，飞行器抗风扰能力较强；

（2）整机尺寸小，机械结构简单，适合飞行器微型化；

（3）拉力由上、下两个旋翼共同提供，因此在承受相同载荷时，旋翼直径可适当缩小，符合微型飞行器的要求。

本文使用PID 控制器设计飞行器高度控制系统。PID控制器由比例环节、积分环节和微分环节构成［22］，其结构简单、可靠性高且易于实现［23］。控制系统闭环框图如图24所示。

图24 控制系统闭环框图Fig.24 Closed-loop block diagram of control system

图24中的高度控制系统由以下几个部分组成：

（1）位置控制器

高度控制器以当前的高度、Z轴方向速度为输入，输出当前所需的升力。由基于欧拉角的飞行控制模型

可以得到无人机高度通道模型

由式（14）以及期望高度动态［24］

可以得到飞行器期望升力fd表达式［24］

由此，得出了无人机期望升力fd与位置、速度信息之间的关系。高度控制器闭环框图如图25所示。

图25 高度控制器闭环框图Fig.25 Closed-loop block diagram of height controller

（2）控制分配器

控制分配器的任务是利用表9 中的旋翼拉力-电场强度关系，将期望升力fd转化为电场强度信息，再结合电池最大电压，输出油门指令σ，因此需要以旋翼拉力作为自变量，得到电场强度随旋翼拉力的变化关系。利用表9 中的数据可以得到电场强度与旋翼拉力之间的关系，如图26所示。

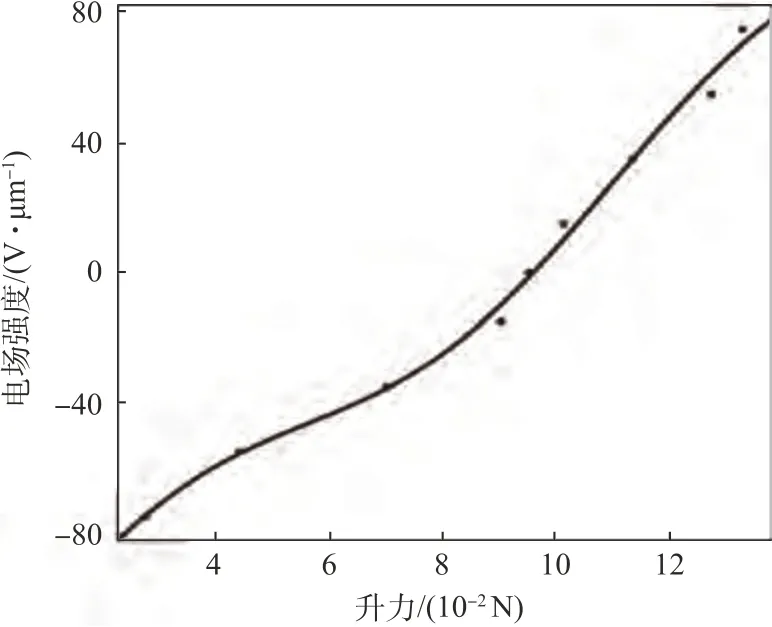
图26 拉力与电场强度关系Fig.26 Relationship between lift and electric field strength

式（14）已给出电场强度为自变量时，旋翼拉力与电场强度间的关系，但由于式（14）非线性较强，很难利用式（14）反解出以旋翼拉力作为自变量时，电场强度随期望升力的变化关系。因此对图26 中的数据进行拟合，可得旋翼拉力f与后缘襟翼内部电场强度E关系式

式中，a1=1468，b1=0.009406，c1=6.199，a2=11.39，b2=0.5865，c2=6.108。近似认为上、下两旋翼提供拉力相等，根据式（19）设计的控制分配器simulink 模型，如图27 所示，升力-电场转换模块如图28所示。

图27 控制分配器Fig.27 Control distribution unit

（3）电源控制器

电源控制器依照输入油门指令σ驱动电池放电，使后缘产生偏角，进而改变无人机升力，电源控制器信号传递图如图29 所示。电源控制器simulink模型如图30所示。

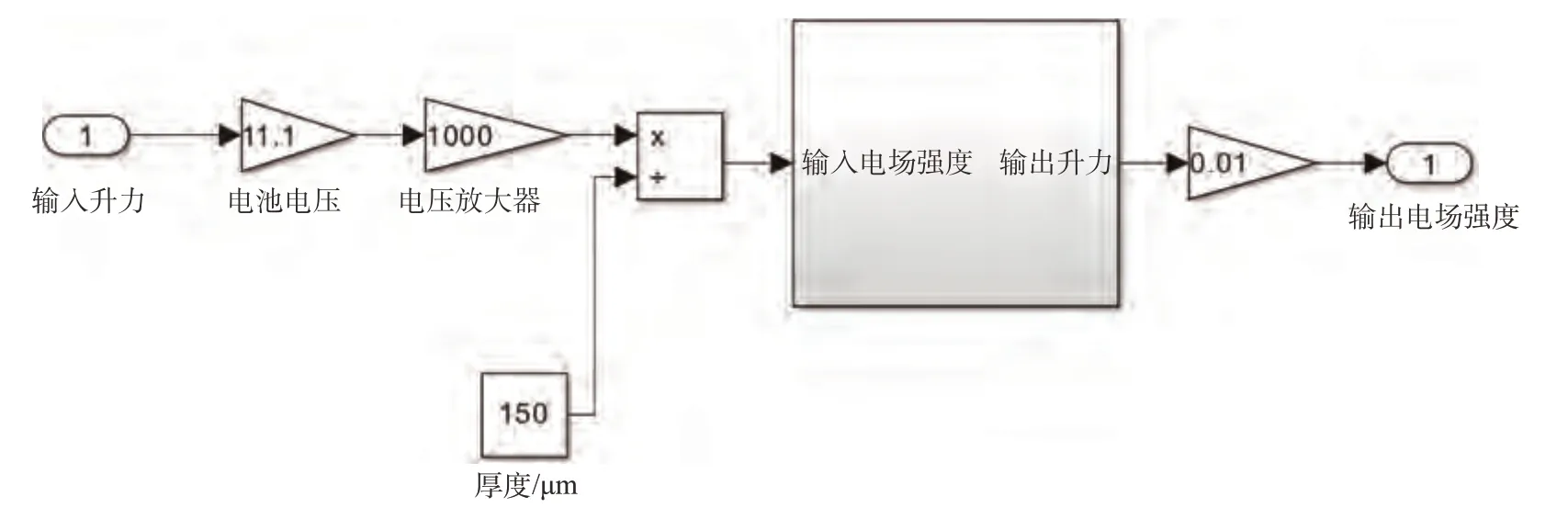
图30 电源控制器simulink模型Fig.30 Power controller Simulink model

（4）无人机部分

无人机部分以当前时刻无人机升力为输入，经过加速度计算以及若干个积分环节，输出无人机当前的加速度、高度以及速度信息。无人机部分的simulink 模型如图31 所示。整个系统的整体仿真图如图32所示。

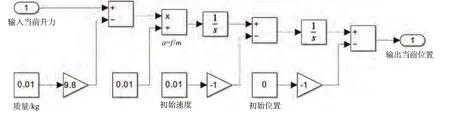
图31 机体部分simulink模型Fig.31 Body part simulink model

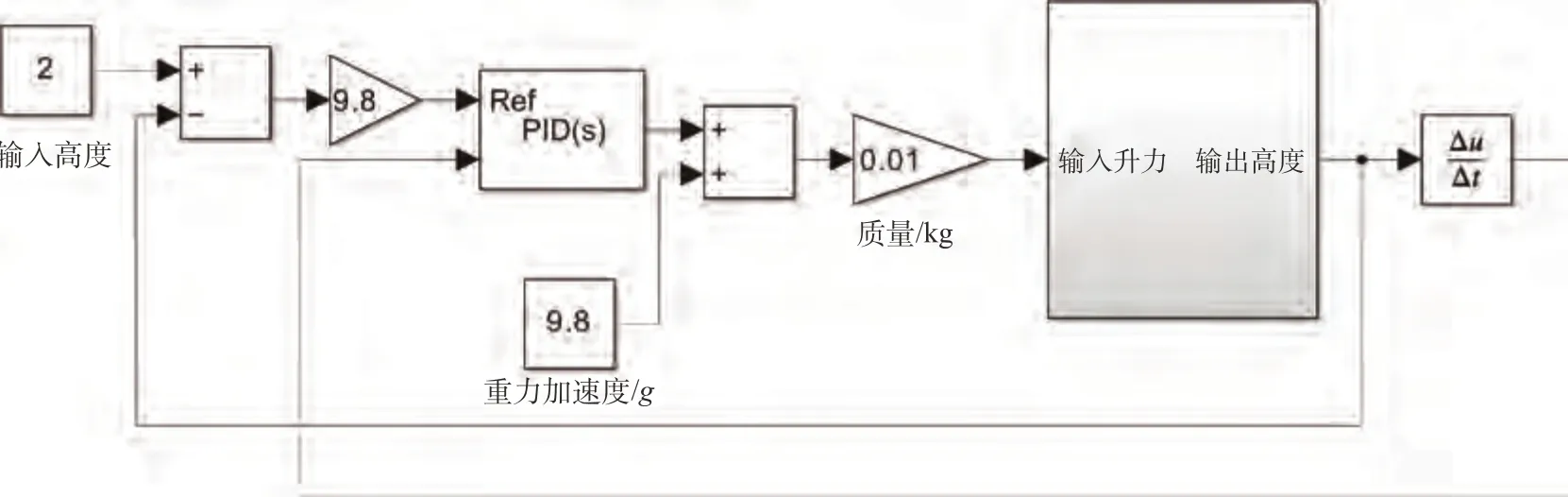
图32 整体仿真图Fig.32 Overall simulation diagram

该系统的初始值参量设置为：初始高度0 m，高度方向初始速度0 m/s，后缘襟翼表面初始电压0 V，目标高度2 m。

飞行器位置响应曲线如图33 所示，动力系统输出电压变化如图34 所示。可以看出，在PID 的控制作用下，无人机的高度以及电源输出电压经过一定时间的调整，都能达到期望的稳定状态，并且超调量较小，响应时间较短，可以实现无人机高度通道的有效控制。

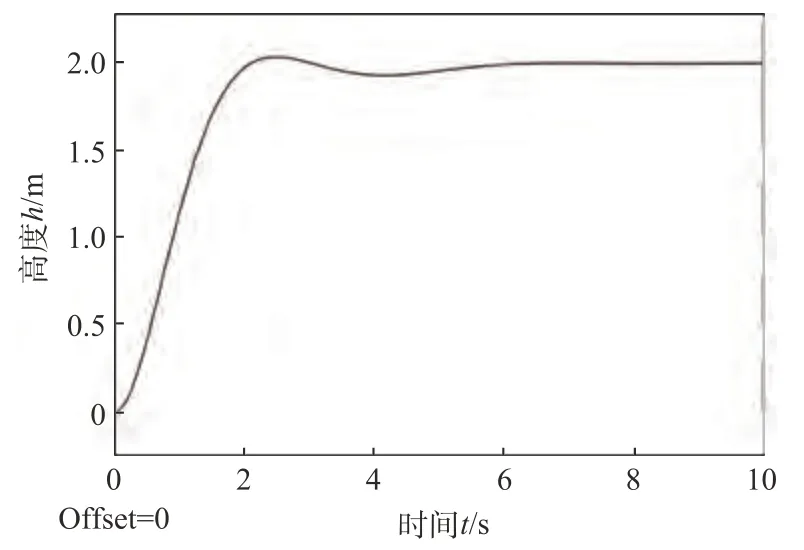
图33 高度响应曲线Fig.33 Height response curve

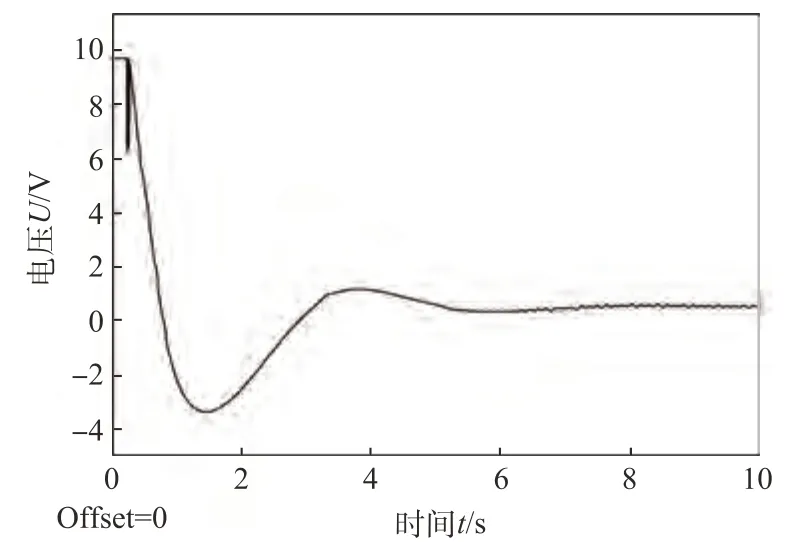
图34 动力系统输出电压Fig.34 Power system output voltage

5 结 论

本文提出了一种新型的旋翼飞行器控制方法，将用P（VDF-TrFE）材料制作的CTEF应用于微型旋翼无人机上，建立一个带有CTEF的微型旋翼模型，采用基于单向流固耦合的方法对其进行推进性能分析，并利用PID 控制器实现旋翼智能控制，实现了智能旋翼飞行器的垂直升降功能。主要得出的结论如下：

（1）对于没有安装CTEF 的微型旋翼，其质量因数随安装角增大，呈先增后减的趋势，在18°安装角处取得最大值；

（2）以P（VDF-TrFE）作为CTEF 的制作材料，在有限元软件中完成仿真模拟。对旋翼施加电压，得到了外加电场与旋翼拉力之间的关系；

（3）利用外加电场与旋翼拉力之间的关系以及PID 控制器建立了高度控制系统，通过改变作用在CTEF表面的电压，实现对无人机高度的有效控制。

同时，本文针对所做工作以及智能变后缘方式存在的一些问题，提出了以下几点展望：

（1）本文在进行流场计算，分析模型推进性能时采用的均为层流模型，但实际情况中，旋翼在旋转时，其表面会存在一部分湍流，这种情况下采用层流模型会造成计算结果不准确，采用转捩模型可以提升流场计算与分析的准确度。

（2）本文在进行连续后缘襟翼仿真模拟时采用的电固耦合方法，无法模拟变电场强度下P（VDF-TrFE）的受力与形变。可以考虑研究变电场强度的P（VDF-TrFE）的电固耦合模型。

（3）本文采用的PID 控制器无法实现参数在线调节，当工作状态发生改变时，控制器无法自动调节参数，使其达到最佳工作状态。可以考虑采用基于模糊PID 算法设计的控制器来解决这一问题，实现PID参数在线调节。

（4）利用柔性材料制作后缘襟翼，可以有效提升后缘襟翼的变形能力，但同时由于受到气动载荷的作用，其控制效果会有一定程度的降低。可以考虑采用优化后缘襟翼结构，或改变后缘襟翼材料的方式解决这一问题，提高后缘襟翼的控制效果。