三维装载约束下基于运输资源共享的车辆路径问题

王 勇,魏远晗,蒋 琼,许茂增

(重庆交通大学 经济与管理学院,重庆 400074)

0 引言

随着城市物流市场需求规模的不断增长和有限的物流配送设施间矛盾的日益凸显,城市物流配送在资源协同性和时间紧迫性上提出了更高的要求,而随着共享运输经济、互用配送模式和共享配送联盟等新兴物流运营模式的兴起,城市物流运输行业在整合物流基础设施资源和提高配送车辆使用率方面进行了有益的探索和应用[1-2]。研究三维装载约束下基于运输资源共享的车辆路径优化问题,有助于完善三维装箱调度理论体系构建以及提高物流资源的集约化利用和促进城市物流系统的绿色可持续发展。国内外学者在三维装载约束下的车辆路径问题相关研究主要集中在三维装箱问题和基于运输资源共享的车辆调度问题两个方面。

在三维装箱问题研究方面,郑炜等[3]研究了考虑货物在车厢中不同摆放状态的三维装箱问题,并设计了一种基于车厢空间分割的启发式算法用于求解问题。吴蓓等[4]为了满足客户不同规格的货物需求,建立了多箱型的三维配载模型并设计了混合启发式算法用于模型求解,有效提高了货箱的空间利用率和配送效率。BORTFELDT等[5]在考虑了三维装箱中的货物重量限制、支撑约束以及卸载顺序等约束,建立了三维装载约束下的车辆路径优化模型,并设计了混合启发式算法求解模型。靳志宏等[6]从三维装载约束的实际出发,考虑了配送车辆的载重约束以及车厢的三维尺寸大小等约束,建立了货物装载与车辆配送路径组合优化的数学模型,并设计了基于CW(Clarke-Wright)节约算法和蚁群算法的交互式混合算法求解模型。FENG等[7]在三维装箱问题中考虑了货箱空间划分策略,建立了以货箱数最少为目标的三维装箱模型,并设计了一种新的混合遗传算法用于模型求解。LI等[8]为了最大化利用车厢空间,研究了货物不同摆放方位的三维装箱问题,构建了以车厢空载体积最小化为目标的三维装载模型,并设计了一种差分进化算法进行模型求解。由上述文献可知,当前关于三维装箱问题的研究主要集中在考虑相关装载约束的模型构建和算法设计方面,且混合启发式算法常被用于研究三维装箱问题,而三维装箱问题为三维装载约束下基于运输资源共享的车辆路径问题研究提供了研究方法切入。

在基于资源共享的车辆调度问题研究方面,王万良等[9]为了解决配送中心车辆不能即时满足客户配送需求的问题,引入车辆共享机制,使得配送中心通过车辆租赁的方式实现了车辆资源的共享,进而实现了物流资源的合理化配置。刘家利等[10]针对企业自身运力有限的情况,提出一种基于车辆租赁的运输资源共享策略,构建了以配送成本最小化为目标的混合整数规划模型,设计了基于CW节约算法的混合遗传算法用于模型求解。ZHANG等[11]针对物流配送网络中的协同运输问题,提出一种基于共享运输资源和客户信息的物流网络协同优化机制,进而降低了运输成本和提高了物流资源利用率。LI等[12]为节约运输资源和提高配送效率,提出通过共享仓库资源实现物流网络的合理化资源配置,进而降低了运输距离和减少了车辆使用数。DENG等[13]提出一种基于物流设施服务能力、运输车辆和客户信息共享的集成优化策略,并证明该策略可以有效降低物流网络运营的总成本和车辆使用数,从而实现物流资源的合理化配置。由上述研究可知,物流企业可以通过车辆租赁、增加车辆使用频次、共享客户信息以及共享仓库资源等方式实现物流资源的共享,进而降低物流运营总成本和节约运输资源,这为车辆调度问题研究中资源共享模式的选择和优化方法的提出提供了理论参考和决策支持。

在三维装箱与运输资源调度组合优化的问题研究方面,GUENTHER等[14]研究了三维装箱和车辆调度的组合优化问题,建立了以最小运输成本为优化目标的数学模型,并设计了基于CW节约算法的蚁群优化算法用于模型求解。章勋宏等[15]为有效降低运输车辆的使用数和提高运输资源利用率,将三维装箱问题与车辆循环取货调度优化问题相结合,建立了多目标优化模型和设计了用于模型求解的启发式算法。王超等[16]研究了三维装箱问题与车辆调度问题的多目标组合优化问题,建立了运输车辆最小化和配送距离最小化的双目标优化模型,并设计了两阶段混合算法进行模型求解。BORTFELDT等[17]构建了混合整数规划模型用于研究运输车辆调度和三维装箱约束的组合优化问题,并提出一种基于遗传算法的混合启发式算法求解模型。吴倩云等[18]研究了装配车间物料配送的集成调度问题,构建了三维装载与车辆运输调度相结合的组合优化模型,并设计了遗传算法进行模型求解,进而提高了车辆的装载能力并节约了运输资源。由上述文献可知,关于三维装箱与运输资源调度问题的组合优化方面取得了一定的研究进展,但将三维装载约束的车厢空间区域划分模式与运输资源共享调度相结合问题的研究方面还有待进一步拓展。

本文考虑了三维装载约束的车辆空间区域划分模式,研究了三维装载约束下基于运输资源共享的车辆路径优化问题。首先,结合客户的多个服务时间窗需求特征,确定客户的多个服务时间周期,并根据客户不同规格的货物需求,选择合理的配送车辆车厢空间区域划分模式;然后,构建了包含配送中心固定成本、配送车辆运输成本、维修成本、租赁成本和违反时间窗惩罚成本的物流运营总成本最小化和车辆使用数最小化的双目标优化模型;其次,设计了一种基于k-means时空聚类算法的Clarke-Wright—非支配排序遗传算法(Clarke-Wright—fast elitist Non-dominated Sorting Genetic Algorithm,CW-NSGA-II)求解模型,该算法引入CW节约算法以提高初始解的质量,并结合NSGA-II算法提高了混合算法寻找优化解的全局和局部空间搜索能力;最后,通过实例分析探讨了三维装载约束下基于运输资源共享的车辆路径优化前后,以及不同车厢空间区域划分模式下的物流运营总成本、车辆使用数、平均装载率和车辆平均使用频次的变化情况,进而为城市三维装载约束下的物流配送问题提供新的研究思路。

1 问题描述

三维装载约束下基于运输资源共享的车辆路径优化问题需要考虑车辆的三维装载约束、客户需求货物类型和客户服务需求时间窗等条件进行运输资源共享调度和车辆路径优化的一类问题。在三维装载物流配送过程中,由于客户的需求货物类型存在差异,且存在多个服务需求时间窗长短不一的现象,导致当前的配送模式存在车辆装载率低、车辆使用数过多和物流运营总成本较高等问题。为了提高车辆装载率,增加车辆使用频次和降低物流运营总成本,需要有效整合物流资源进行合理的货物装载和配送调度,进而结合三维装载约束、车辆载重和客户访问时间窗等约束条件构建物流运营成本最小和车辆使用数最小的双目标优化模型,研究三维装载约束下基于运输资源共享的车辆路径优化问题。为了更清楚地说明三维装载约束下基于运输资源共享的车辆路径优化问题,本研究结合调研数据绘制了一类基于运输资源共享的三维装载物流配送优化方案前后对比图,如图1所示。

图1 基于运输资源共享的三维装载物流配送优化前后对比

图1a表示基于运输资源共享的三维装载车辆路径优化前,配送中心服务客户配送线路的各服务时间窗存在时间交错和重叠等现象,且存在交错运输和较多违反服务时间窗的客户点,进而导致配送车辆使用数较多和物流运营成本较高等现象。图1b表示基于运输资源共享的三维装载车辆路径优化后,具有相近服务时间窗的客户在一个聚类单元内接受配送服务,结合客户不同规格的货物需求进行车厢分区和货物装载方式优化,进而提高了车辆使用频次,且消除了违反时间窗的惩罚成本。假设单位时间的配送成本为40元,违反时间窗的单位时间惩罚成本是15元,车辆的租赁费用为100元/辆。基于假设数值并结合考虑运输资源共享的三维装载车辆路径优化前后路段通行时间、违反时间窗时间和车辆使用数,计算得到基于运输资源共享的三维装载车辆路径优化前后配送时间、车辆数量和运营成本等指标的比较结果,如表1所示。结果表明基于运输资源共享的三维装载车辆路径优化后有效降低了物流运营总成本,减少了共享车辆使用数和配送线路数,消除了违反时间窗的客户点,降低了车辆配送时间和配送成本,增加了车辆平均使用频次。

表1 基于运输资源共享的三维装载车辆路径优化前后对比

2 模型建立

2.1 符号定义

本文研究涉及到的一些变量和符号定义如表2所示。

表2 变量定义

2.2 模型构建

本文以配送中心的物流运营成本Z1最小化和配送车辆使用数Z2最小化为优化目标,建立了具有普适性的三维装载约束下基于运输资源共享的车辆路径优化模型。

(1)

(2)

约束条件：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

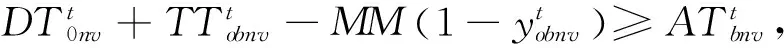
(11)

(12)

(13)

(14)

(15)

(16)

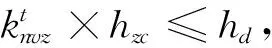
(17)

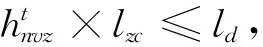
(18)

(19)

(20)

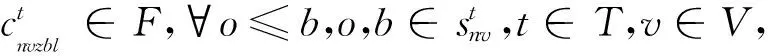
(21)

(22)

(23)

(24)

(25)

其中：式(3)表示服务周期t内每个客户点仅接受一辆配送车辆服务;式(4)表示每个客户在服务周期t内仅接受一条配送线路服务;式(5)表示配送车辆将货物送达客户后必须离开;式(6)表示消除子回路约束;式(7)表示服务周期t内配送车辆v的使用次数等于其配送线路数之和;式(8)表示在服务周期t内配送车辆v上各区域内货物数量的约束;式(9)表示在服务周期t内配送车辆v上装载货物的总重量不超过配送车辆的最大装载量;式(10)和式(11)表示配送车辆到达客户点的时间,式(12)和式(13)表示配送车辆离开和到达配送中心的时间必须在其服务时间窗内;式(14)～式(16)表示货物必须摆放在车厢内;式(17)～式(19)表示配送车辆任何区域内装载货物长宽高的加和不能超出区域长宽高的限制;式(20)表示后服务客户的货物不能压在先服务客户货物的上面;式(21)表示后服务客户的货物不能挡在先服务客户货物的前方;式(22)～式(25)表示变量约束。

3 CW-NSGA-II混合算法

3.1 算法过程描述

本文设计了基于k-means时空聚类的CW-NSGA-II混合算法求解三维装载约束下基于运输资源共享的车辆路径优化模型。首先,结合客户的服务时间窗,利用k-means时空聚类算法[19]确定客户的多个服务周期,在相应服务周期内,选取k个聚类中心,计算每个客户点到聚类中心的时空距离,并将客户点指派到最临近的聚类中心;然后,结合帕累托优化原理设计适应度函数并计算适应度函数值[20-21],并应用CW节约算法[22]生成初始的配送方案;最后,应用NSGA-II算法[23]进行配送方案优化和非支配排序优化,进而生成配送路径和三维装载方案。CW节约算法和NSGA-II算法的集成旨在利用CW节约算法获得质量较好的次优解,进而提高混合算法寻找优化解的全局和局部空间搜索能力,从而更有效地收敛到最优解。在混合算法设计过程中集成了聚类算法和智能算法间的选择性赋予机制,进一步提高了算法的寻优能力。基于k-means时空聚类的CW-NSGA-II混合算法的流程图如图2所示,具体算法步骤如表3所示。

表3 基于k-means时空聚类的CW-NSGA-II混合算法步骤

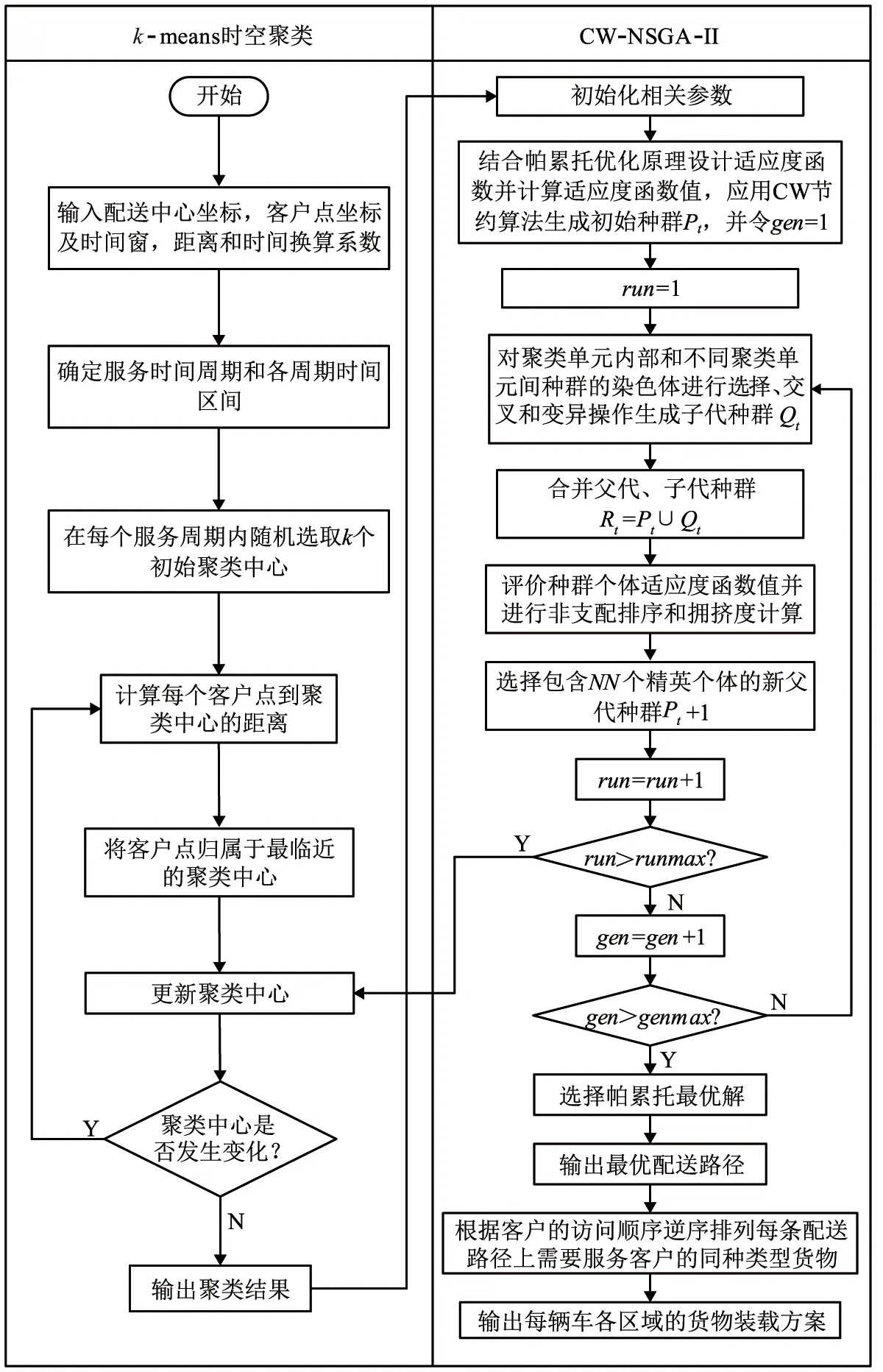
图2 混合算法流程图

3.2 基于k-means的时空聚类

客户聚类是获得更好的物流网络配置和确保货物高效配送的方法[19]。k-means算法传统上是基于欧几里得距离、余弦距离等对客户进行聚类,本文在传统k-means算法的基础上结合客户服务时间窗设计了距离函数,首先在时间范围[t1,t2]内对客户进行聚类,然后再考虑空间范围,将客户点指派到最临近的聚类中心,如图3所示。

图3 k-means时空聚类示意图

客户点间时空距离的计算如下：

Dob=|xo-xb|+|yo-yb|+δ|t1o-t1b|+
δ|t2o-t2b|,o,b∈O。

(26)

式中：x,y表示地理坐标;t1,t2表示时间窗;δ表示距离与时间的转换系数。

3.3 CW-NSGA-II混合算法设计

本研究设计了CW-NSGA-II混合算法用于求解三维装载约束下基于运输资源共享的车辆路径优化模型。NSGA-II是一种基于群体的启发式算法[24-25],通常用于解决多目标问题,CW算法用于生成初始种群,整个优化过程在NSGA-II算法的基本框架上进行设计,并通过帕累托前沿进行双目标解的帕累托优化解排序,进而通过排序选取帕累托优化解并输出双目标最优解,这样既能保证初始解的质量,又可以很好地解决本文提出的双目标模型。

3.3.1 编码方式

针对三维装载约束下基于运输资源共享的车辆路径优化问题,本研究采用整数编码的方式构造共享车辆的配送路径染色体。假设配送中心为6个客户提供配送服务,其初始配送安排如图4所示。其中0表示配送中心,其余整数表示各客户。根据配送车辆空间各区域装载货物的最大数量、车辆最大载重能力以及客户的时间窗等约束,用自然数0对染色体进行解码,形成相应的子路径。由图3可知,该染色体可解码为[0,2,4,3,0]与[0,6,5,1,0]两条子路径,即配送车辆V1的配送路径为：配送中心0→客户2→客户4→客户3→配送中心0;配送车辆V2的配送路径为：配送中心0→客户6→客户5→客户1→配送中心0。

图4 染色体编码和路径解码说明

3.3.2 交叉操作

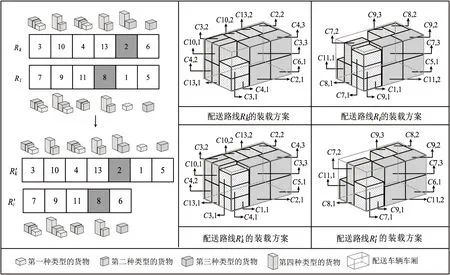
图5 2-opt*交叉操作过程

3.3.3 变异操作

变异操作是在选择、交叉生成的种群中随机选择一条染色体,并使染色体上随机选择的两个基因发生突变,产生新的染色体的过程。其步骤如下：首先,根据突变概率值Pm随机选择父代中的一个染色体;然后,在父代染色体中随机选择两个基因进行交换,交换后产生一个新的子代染色体。变异操作后,判断配送车辆路径所对应的车辆装载方案是否符合相关约束条件,若不符合,则应重新进行变异操作。变异过程如图6所示。

图6 变异过程

3.4 算法检验

将CW-NSGA-II混合算法、多目标和声搜索算法(Multi-Objective Harmony Search Algorithm,MO-HSA)[27]和多目标蚁群算法(Multi-Objective Ant Colony Optimization,MO-ACO)[28]进行比较,实验数据是在所罗门数据集基础上增加客户货物需求个数而来,具体实验数据参数如表4所示。算法参数设置如下：CW-NSGA-II、MO-HSA和MO-ACO算法中的种群规模popsize=100,最大迭代次数maxgen=200,精英迭代次数maxrun=20,精英染色体个数NN=30,选择概率Ps=0.9,交叉概率Pc=0.9,变异概率Pm=0.1;MO-HSA算法中和声库大小HMS=100,和声记忆库保留概率HMCR=0.9,扰动概率PAR=0.1,音调微调幅度BW=0.000 5;MO-ACO算法中信息素重要程度α=1,启发式因子重要程度β=10,信息素蒸发系数ρ=0.5。将每种算法分别运行30次,选取最优的物流运营总成本和车辆使用数以及对应的求解时间,如表5所示。

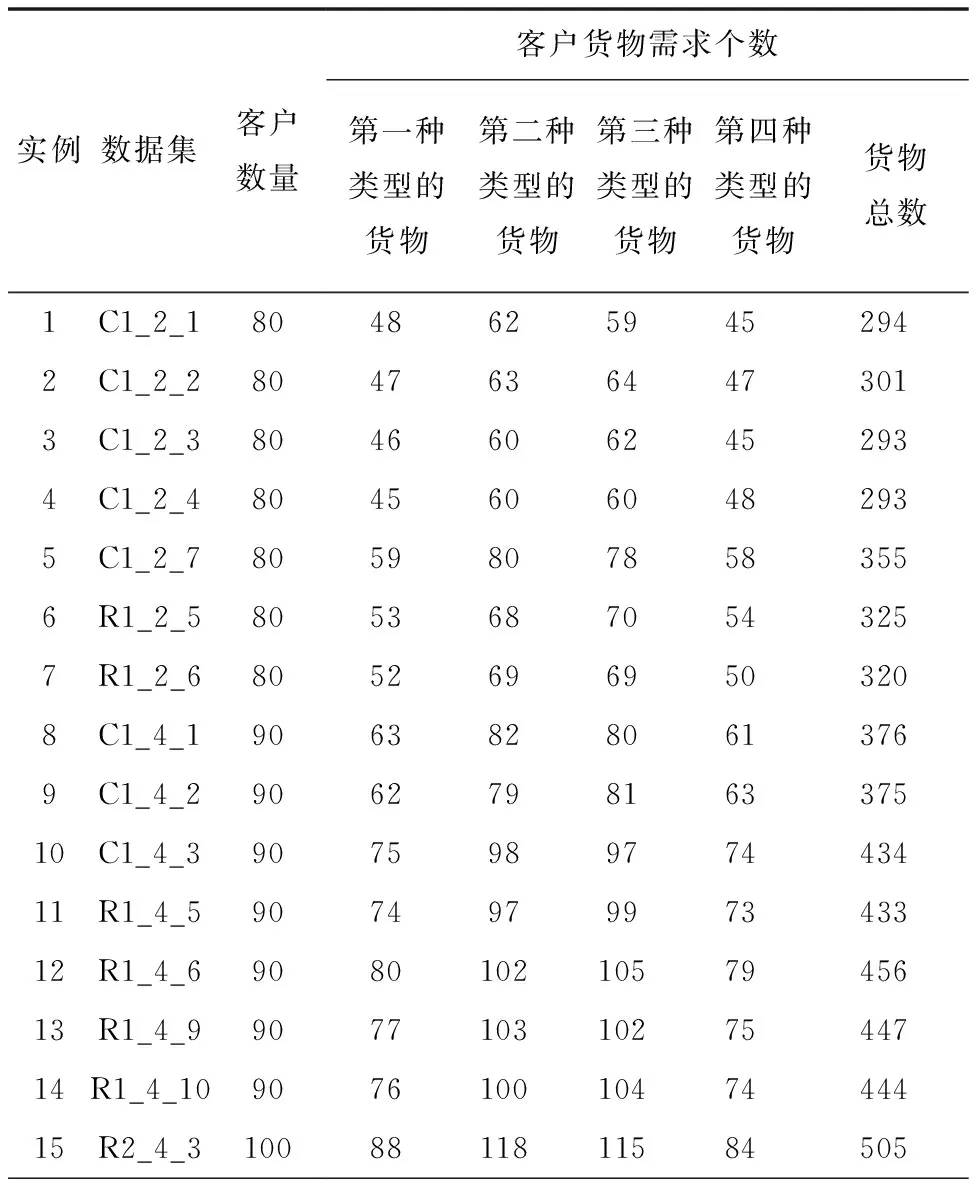
表4 实验数据参数表

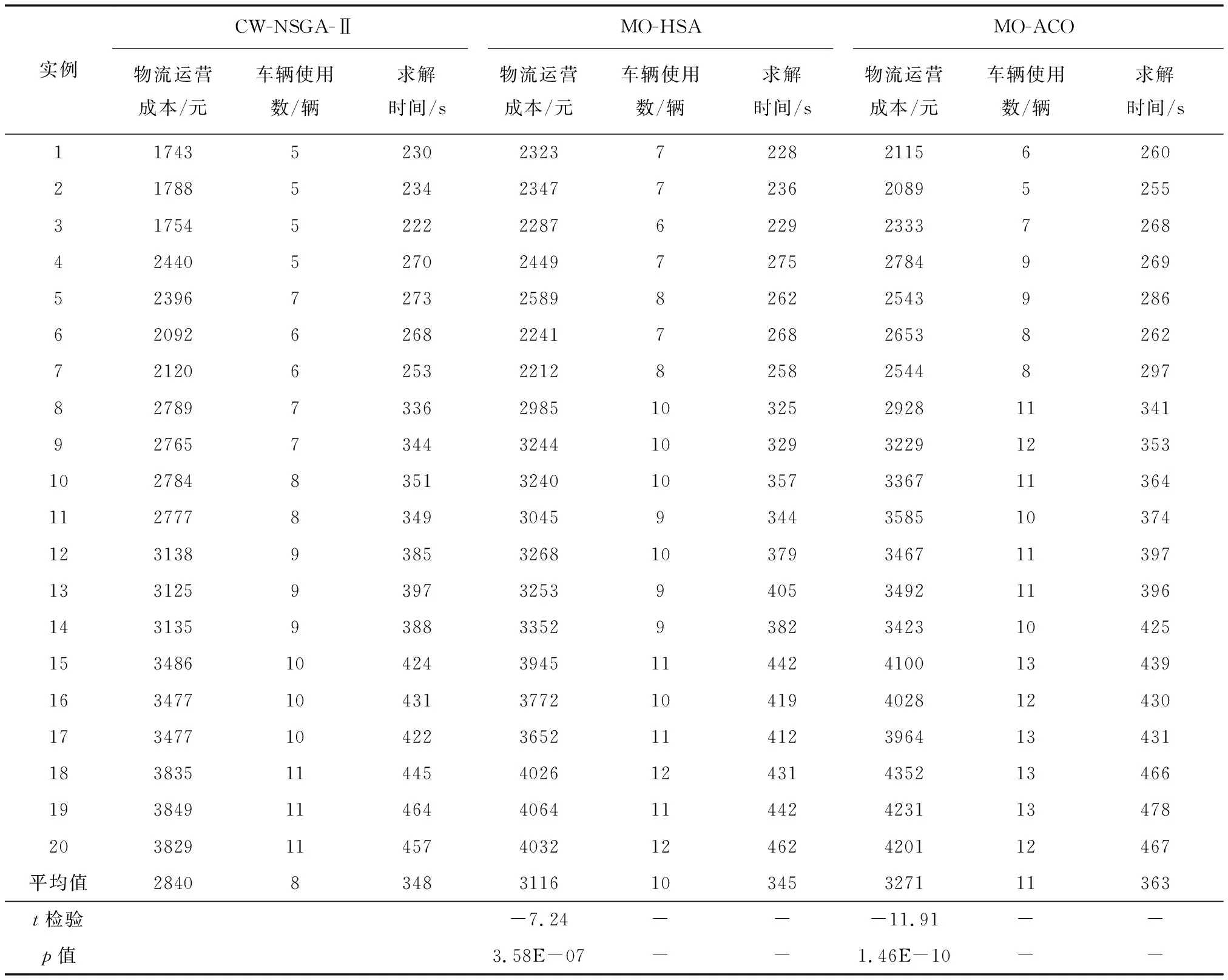
表5 不同算法优化结果的比较

由表5可知,CW-NSGA-II算法、MO-HSA算法与MO-ACO算法的最小物流运营成本的t检验和p值的比较结果表明,CW-NSGA-II算法的最小物流运营成本与其他两种算法相比具有显著差异性。此外,在物流运营成本和车辆使用数方面,CW-NSGA-II算法均优于MO-HSA算法和GA-ACO算法,CW-NSGA-II混合算法计算的物流运营成本平均值比MO-HSA降低了8.86%,比MO-ACO降低了13.18%。在20组实例的求解平均时间方面,CW-NSGA-II混合算法比MO-HSA多耗时3 s,但是物流运营成本和车辆使用数均优于后者。

4 算例分析

4.1 算例相关数据

以重庆市某配送中心(DC)及其服务的120个客户点(C1～C120)为例进行研究,相应的地理位置分布如图7所示。配送中心所服务客户的商品需求类型存在差异,且其中一部分客户有多个服务时间窗,具体如表6所示。配送中心负责配送的货物类型有4种,相应的车厢空间根据货物规格大小划分为4个区域,各个区域大小、每种类型货物的规格、重量和每个车厢区域可装载的货物数量如表7所示。

表7 各个区域大小及其装载货物的规格、重量和可装载的货物数量

图7 配送中心与客户点地理位置分布图

4.2 结果与分析

在现有文献[29-30]和多次实验计算的基础上,相应参数设置如下：车厢长L=4 m,车厢宽W=2 m,车厢高H=2 m,车辆最大载重量Q=700 kg,车辆最大装载体积V=16 m2,车辆租赁成本rv=100 元/辆,车辆维修成本mv=30 元/辆,单位体积固定成本f=0.2 元,配送车辆单位距离行驶成本cv=0.8,车辆数V=12,车辆早到单位时间惩罚系数λ1=15,车辆晚到单位时间惩罚系数λ2=20。如表8所示为三维装载约束下基于运输资源共享的车辆路径优化前后运营成本、车辆使用数以及车辆平均装载率等的变化情况。

表8 三维装载约束下基于运输资源共享的车辆路径优化前后结果对比

由表8可知,车辆路径优化前后,车辆使用数减少了68.42%,车辆租赁成本降低68.42%,配送线路数减少5.3%,车辆平均使用频次提高200%,时间窗违反时间减少84.62%,违反时间窗惩罚成本降低84.29%,配送时间减少了9.8%,配送成本降低了27.97%,物流运营成本节约了48%,平均装载率提高8.69%。此外,本文选取了车辆使用数、平均装载率、违反时间窗的惩罚成本,物流运营成本和车辆平均使用频次等指标,绘制了各个指标优化前后的对比图,如图8所示。由图8可知,优化后车辆使用数、违反时间窗的惩罚成本和物流运营成本均大幅减少,而平均装载率和车辆平均使用频次有所增加。

本文将客户时间窗划分为3个服务周期进行研究,在每个服务周期内,应用CW-NSGA-II混合算法求解了三维装载约束下基于运输资源共享的车辆路径优化问题,求得各服务周期的优化配送方案,各共享车辆的平均装载率以及不同共享频次的车辆平均装载率,具体结果如表9所示。

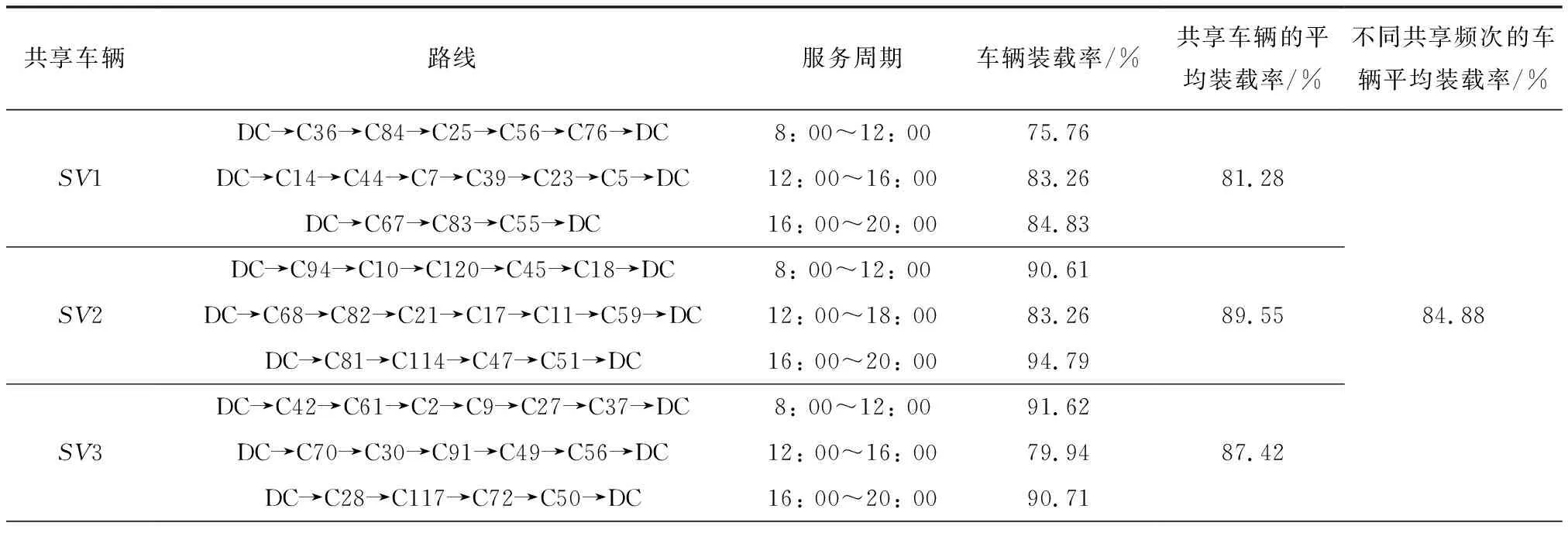
表9 三维装载优化后共享车辆配送方案

续表9

由表9可知,以物流成本最小化和车辆使用数最小化为目标进行优化研究,优化后的配送方案中,配送中心需要派遣12辆车对120个客户进行配送服务。在三维装载优化过程中,配送车辆SV1～SV10均在3个服务周期进行了车辆共享,而配送车辆SV11和SV12均在2个服务周期进行了车辆共享。此外,3个服务周期内共享车辆(SV1～SV10)的平均装载率为84.88%,2个服务周期内共享车辆(SV11和SV12)的平均装载率为80.92%。

此外,本研究选取了车辆在共享次数为3情况下平均装载率最高的共享车辆9和车辆在共享次数为2情况下平均装载率最高的共享车辆11,分别绘制了它们在各个服务周期的三维装载图,如图9和图10所示。共享车辆9和11在各服务周期的各区域装载率和整车厢装载率如表10和表11所示,并绘制了共享车辆9和11在各服务周期的各区域装载率和整车厢装载率的对比图,如图11和图12所示。

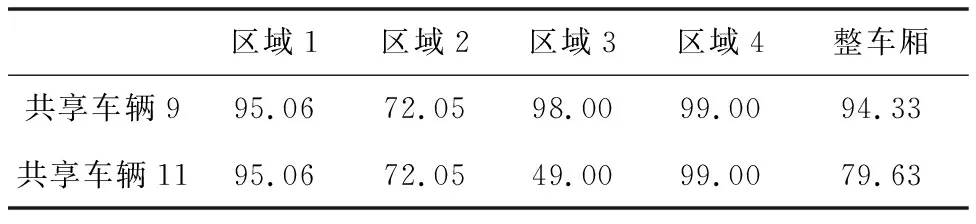
表10 第一服务周期[8,12]内SV9和SV11的装载率对比 %

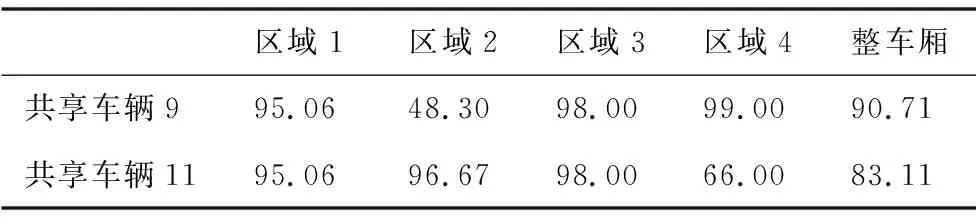
表11 第二服务周期[12,16]内SV9和SV11的装载率对比 %

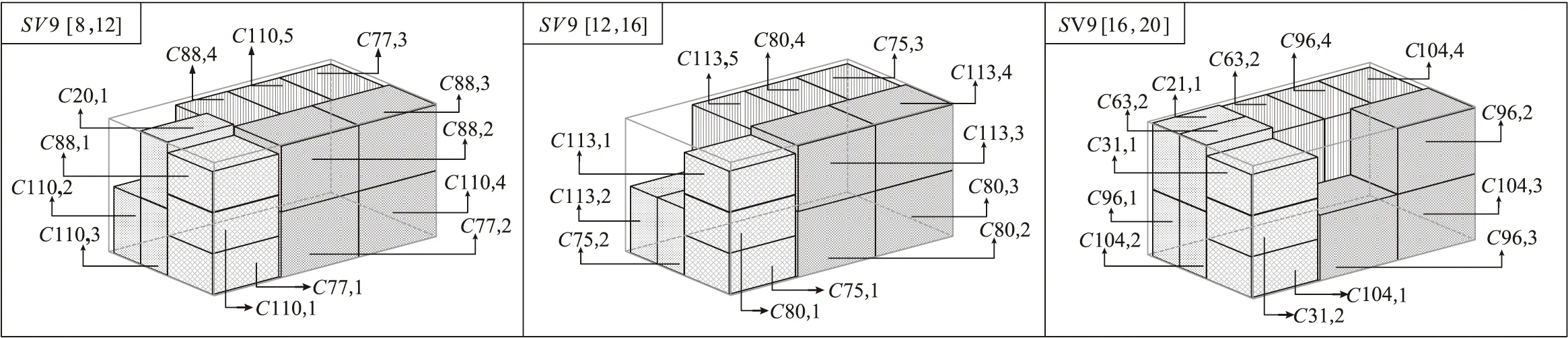
图9 SV9在各服务周期配送方案的三维装载图

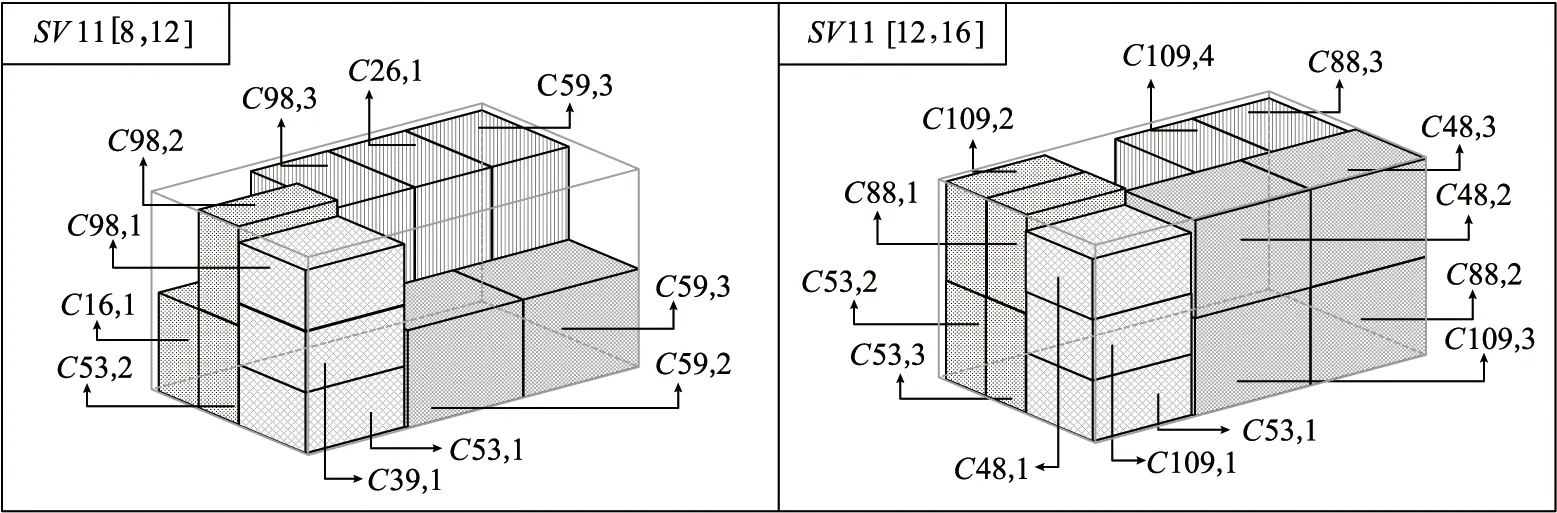
图10 SV11在各服务周期配送方案的三维装载图

图11 第一服务周期[8,12]内SV9和SV11的装载率对比

由图11可知,共享车辆9和共享车辆11在第一服务周期内,区域1的装载率均为95.06%,区域2的装载率均为72.05%,区域4的装载率均为99%,共享车辆9区域3和整车厢的装载率比共享车辆11分别高49%和14.7%。由图12可知,共享车辆9和共享车辆11在第二服务周期内,区域1的装载率均为95.06%,区域3的装载率均为98%,共享车辆9区域2的装载率比共享车辆11低48.37%,而区域4和整车装载率比共享车辆11分别高出33%和7.6%。综上所述,共享车辆的区域装载率和整车厢装载率会随着服务周期和车辆使用频次的改变而发生变化,且提高共享车辆的使用频次可以有效提高共享车辆的平均装载率。

4.3 分析与讨论

三维装载约束下基于运输资源共享的车辆路径优化问题是以物流运营成本和车辆使用数为优化目标,不同车厢空间的分区模式通过影响货物在车厢中的装载方式,进而影响车辆使用数和物流运营成本。为了进一步研究不同车厢空间分区模式对优化目标的影响,本文假定车厢空间平均分成2个区域、3个区域、4个区域和按货物规格大小分成4个区域4种模式,考虑到车厢分区会增加配送车辆上的操作时间和成本,本研究假定车厢最大的空间区域划分数为4,不同车辆空间分区模式如图13所示。4种模式下平均装载率,物流运营成本,车辆使用数和车辆平均使用频次的变化情况,如表12所示。不同车厢空间分区模式下平均装载率、物流运营成本、车辆使用数以及车辆平均使用频次的对比如图14所示。

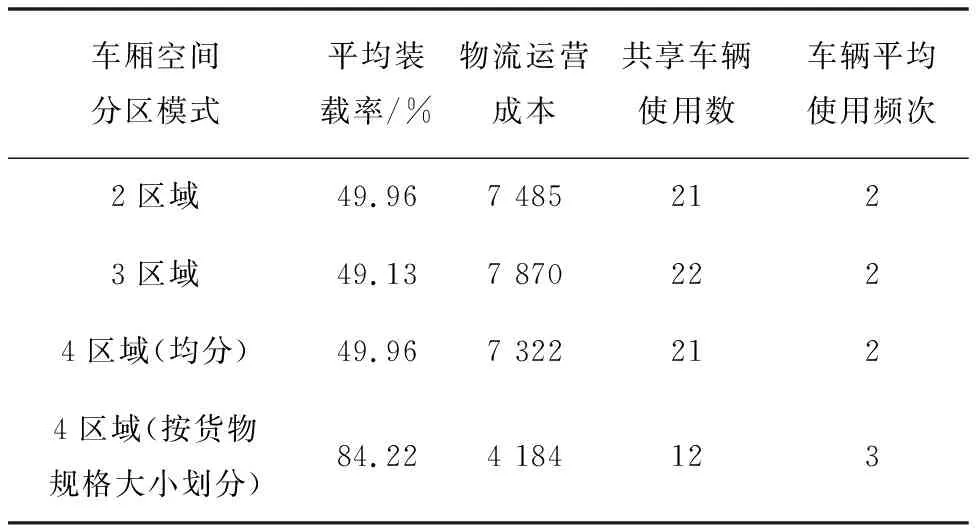
表12 不同车厢空间分区模式下优化结果对比

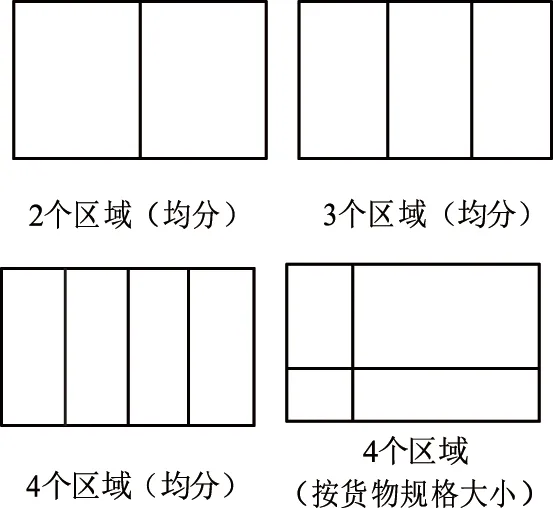
图13 不同车厢空间分区模式

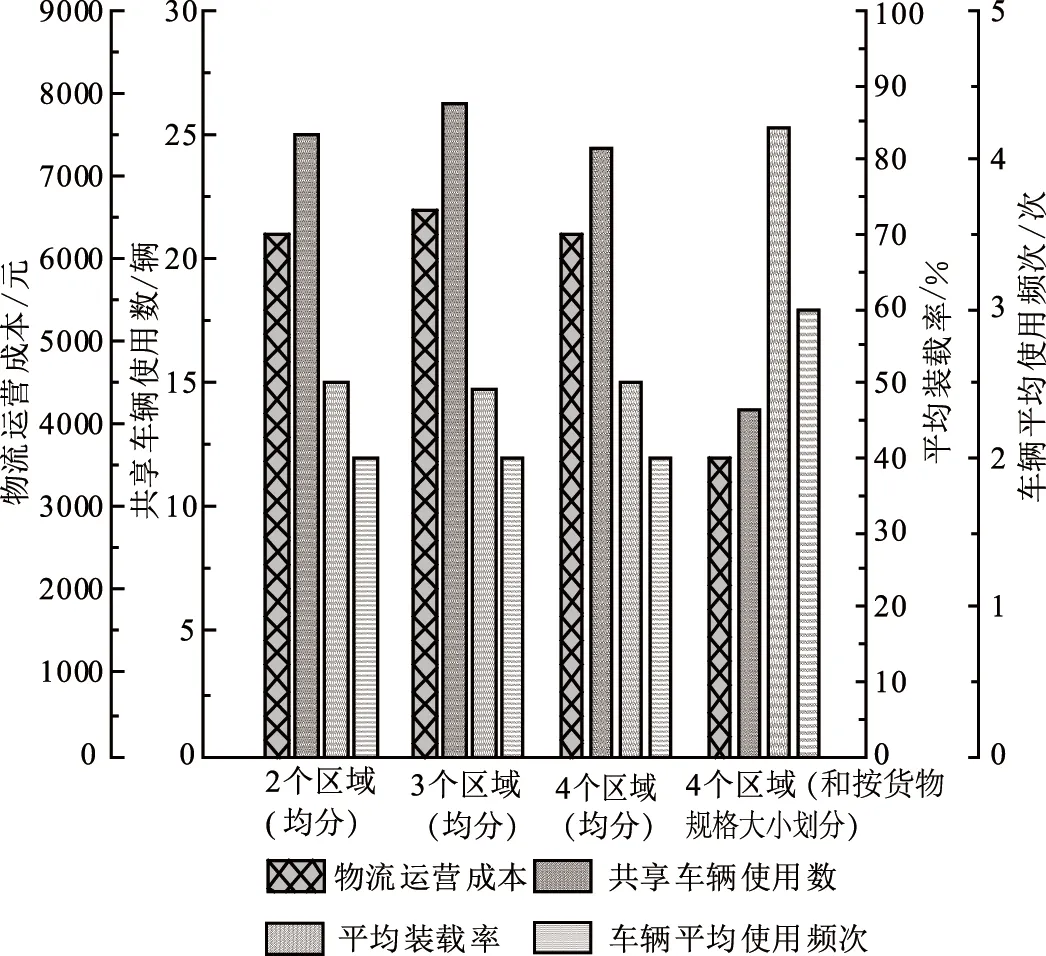
图14 不同车厢空间分区模式下优化结果对比

由表12和图14可知,当共享配送车辆的车厢空间按照货物规格大小分为4个区域时,可得到最少的车辆使用数、最低的物流运营成本、最高的车辆平均装载率和最多的共享车辆使用频次。而将车厢空间平均分成2个区域,3个区域和4个区域3种情况相比于车厢空间按货物规格大小分成4个区域,物流运营成本分别增加了3 301元、3 686元和3 138元,车辆使用数分别增加了9辆、10辆和9辆,平均装载率分别减少了34.26%、35.09%和34.26%,车辆平均使用频次均减少了1次。综上所述,按货物规格大小进行合理的空间区域划分可以有效地降低物流运营成本,减少车辆使用数,增加车辆平均装载率和提高车辆使用频次。

5 结束语

本文研究了三维装载约束下基于运输资源共享的车辆路径优化问题,首先,结合客户多个服务时间窗的需求和空间地理位置进行合理的服务周期划分和k-means时空聚类,并在每个聚类单元内根据客户不同规格货物需求和服务时间窗进行合理的配送车辆调度和货物装载方式优化。其次,建立了包含配送中心固定成本、配送车辆运输成本、维修成本、租赁成本和违反时间窗惩罚成本的物流运营总成本最小化和配送车辆使用数最小化的双目标优化模型。然后,设计了一种基于k-means时空聚类的CW-NSGA-II混合算法求解模型,该算法引入CW节约算法以提高初始解的质量,并结合NSGA-II算法提高了混合算法获取优化解的全局和局部空间搜索能力,并在混合算法过程中设计了聚类算法和智能算法间的选择性赋予机制,进一步提高了混合算法的寻优能力。最后,将CW-NSGA-II混合算法与MO-HSA混合算法、MO-ACO混合算法进行了对比分析研究,验证了本研究提出的混合算法的有效性和合理性。

本文结合重庆市某配送中心的三维装载物流配送实际数据,通过模型求解对各类不同需求客户的货物运输配送路线和装载方式进行了联合优化,进一步验证了模型与算法的可行性。计算结果表明,相对于优化前的车辆路径方案,三维装载约束下基于运输资源共享的车辆路径优化方案的物流运营成本和车辆使用数分别减少了48%和68.42%,违反时间窗的惩罚成本降低了84.29%,平均装载率提高了8.69%。本文在实际算例的基础上探讨了不同空间分区模式下物流成本、车辆使用数、平均装载率以及共享车辆使用频次的变化情况。研究表明,根据客户需求货物种类数和不同种类货物的规格大小划分配送车辆车厢空间区域,能有效降低物流运营总成本,减少配送车辆使用数,且提高共享车辆使用频次可以有效提高车辆平均装载率。本研究为基于运输资源共享的三维装载物流网络优化问题研究提供了相应方法借鉴,未来研究将结合收集装载问题、客户动态需求装载问题以及多车型协同调度装载问题研究三维装载约束下基于运输资源共享的车辆路径问题,进而丰富三维装箱调度理论并拓展其应用领域。