滑块式球形转子泵的振动抑制研究

李世林，白国长

(郑州大学机械与动力工程学院，河南郑州 450000)

0 前言

球形泵属于回转式容积泵，其转子的形状为球形，可实现超微型化、高可靠性的容积式动力机械，在压缩机和液压泵领域得到了相当广泛的应用。滑块式球形动力机械理论体系及知识产权体系，是由王陆一、李正平[1]原创发明的、具有颠覆性意义的动力机械原理的开拓性发明成果；利用此原理研制出来的球形微型液压泵结构简单，运行稳定、变工况性能好，能实现超小体积、高压力，可用于机器人、工程机械、机床工业、航空航天、VR装备等产业。

但是由于滑块式球形泵的旋转盘做往复式运动，在工作时会产生陀螺力矩，是球形泵机械振动的主要来源。而且，滑块式球形泵的容积效率高，一周双排量的特性，产生较大的流量脉动，必然会造成振动加剧，降低驱动的平顺性，影响泵的性能和使用寿命，对滑块式球形泵的振动进行研究尤为必要。目前国内外对球形泵的研究相对较少，西安交通大学的GUAN等[2]对一种偏置转子式球形泵的运动学和动力学进行了深入研究，结果显示由于没有往复运动的部件，球形泵的噪声只有传统电磁泵的1/4。南洋理工大学的CHEN等[3]研究了柱塞泵的动态振动特性，发现机械振动幅值随着转速和扭矩的增大而增大。康考迪亚大学的BAHR等[4]建立了一个数学模型来研究恒功率调节斜盘轴向柱塞泵的振动特性，发现在横向力矩的激励作用下，比例阀芯以与力矩相同的频率周期性振动。本文作者研究的滑块式球形泵存在往复运动件，采用双泵抵消力矩的方法减小机械振动，并研究双泵对流量脉动的影响。

1 球形转子泵的振动机制

球形转子泵的核心是转子机构，主轴上沿径向有一条滑槽，旋转盘下端的滑块插入滑槽形成平面副，旋转盘通过销轴与活塞连接，活塞顶部的轴与缸盖孔连接，活塞的轴相对于垂直方向有一个角度α，称之为活塞角。主轴驱动旋转盘，旋转盘带动活塞绕其自身轴线旋转。而旋转盘的运动是两种运动组合的结果：一个是围绕着主轴轴线的旋转，另一个是相对滑槽面的往复摆动，造成机械振动。

缸盖、缸体和球形转子形成密封空间，当主轴转动时，容积腔体积变化，起到吸排液体的作用[2]。由于球形转子运动的非线性，流量并不是均匀的，产生流量脉动。

图1 球形转子泵

2 球形泵动力学分析

2.1 动力学建模

根据滑块式球形泵的结构和工作原理，其结构简化模型见图2。活塞绕轴线2旋转；旋转盘的运动可分解为两种：(1)绕旋转轴1做角速度为ω的匀速转动，其为绝对运动；(2)滑块在滑槽平面以点O为圆心做往复钟摆运动，轨迹为A″-A1-A′，其为相对运动。建立两个原点都位于球心点O的空间直角坐标系xyz和x′y′z′，x′y′z′坐标系是xyz坐标系绕x轴旋转角度α得到[2，5]。

A是旋转盘滑块中心，B是销轴轴线的外端点，销轴半径r，且OA=OB=R，R是球形转子的半径。假设滑块中心在z轴上时为球形泵的参考起始状态C-A1-B1-D，驱动主轴从C-O′-A1转到C-O″-A，在平面xoy上的角位移记为θ，销轴从O-B1旋转到O-B，在平面x′oy′上角位移记为φ。OB与z轴夹角为σ1，OA与z轴夹角为旋转盘摆角σ2。

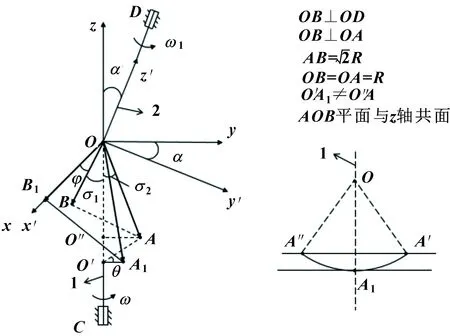
图2 球形转子泵简化模型

在xyz坐标系中，点A的位置可以表示为

(1)

点B在x′y′z′坐标系的位置可以表示为

(2)

将式(2)通过坐标变换方法用xyz坐标系表示为

(3)

同时zB可以用σ1表示为

zB=-Rcosσ1

(4)

联合求解式(3)和式(4)可以得到：

σ1=arccos(sinφsinα)

(5)

又因为OB与OA呈90°，所以σ1+σ2=90°，解得摆角σ2为

(6)

当旋转主轴以等角速度ω旋转时，活塞也将以角速度ω1运转，且ω1的大小会随着旋转主轴的转角θ的改变而改变[6]，则有：

(7)

将上式(7)对时间t进行求导，且dθ/dt=ω，可以得到活塞的角速度ω1：

(8)

对式(8)的角速度ω1再次求导就是活塞的角加速度ε1：

(9)

将式(7)代入式(6)中，并对σ2关于时间t求导可以获取滑块摆角的角速度ω2和角加速度ε2：

ω2=

(10)

(11)

2.2 转子力矩分析

2.2.1 活塞的惯性力偶矩

周期性变化的角速度ε1的存在，使得活塞需要承受相应的惯性力偶矩M2的作用，力矩方向沿活塞轴2，则根据活塞的运动特性，活塞的惯性力偶矩M2[7]可以表示为

(12)

式中：J2是活塞对转轴2的转动惯量。

2.2.2 旋转盘陀螺效应分析

当高速转动部件的转动轴在空间中改变方位时，转动部件必对约束部件作用一个附加力偶，影响系统的稳定性，这种现象称为陀螺效应，附加力偶的矩称为陀螺力矩[8-9]。由上一节的分析可知，旋转盘的运动存在陀螺力矩，建立研究其陀螺力矩的动力学模型，如图3所示。

图3 旋转盘陀螺效应动力学模型

旋转盘滑块的点A绕着其旋转轴3，以角速度ω2做自转运动，点A的轨迹为图3圆弧4上的a0-a1段；旋转轴3绕旋转轴1以角速度ω做匀转速运动，此为旋转轴3的公转，旋转轴3在过原点O且与轴1垂直的平面5上。旋转盘在运动过程中有图3所示的陀螺力矩M1产生，与轴线1和轴线3垂直。

根据陀螺力矩的计算公式推导出该球形泵的陀螺力矩M1：

M1=J1×ω×ω2

(13)

式中：J1是旋转盘对旋转轴3的转动惯量。

研究式(13)可知，当J1为定值时，旋转盘的陀螺力矩M1由旋转盘滑块的摆角速度ω2和ω决定，而根据式(10)，ω2的大小跟ω有关，所以陀螺力矩M1的大小取决于主轴转速ω的值。将ω和ω2代入，得到陀螺力矩：

M1=J1·

(14)

2.2.3 空间力矩的合成

利用解析法将陀螺力矩M1和惯性转矩M2在xyz坐标系上分解[7]：

(15)

(16)

根据合力矢投影定理：

(17)

则可以得到合力偶矩矢的大小：

(18)

a、b、c分别是合力矩矢M与x、y、z轴的正向夹角，则合力偶矩矢的方向：

(19)

力矩分布曲线如图4所示，活塞惯性转矩为正弦周期分布。在转角θ为90°和270°时的陀螺力矩M1是最小值为0；在0°和180°时达到最大值，且M1(0°)=M1(180°)。合成力矩M基本上与陀螺力矩M1曲线重合，说明球形泵整体所受力矩的大小主要取决于旋转盘陀螺力矩M1的值。

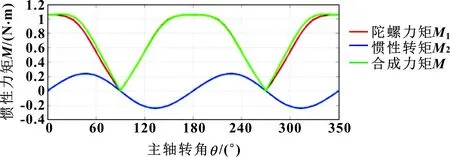
图4 力矩曲线

3 球形泵容积

根据主轴转角、转盘偏角、活塞转角3个参数，可推导出工作腔(容积腔)张角，进而求得工作腔容积的变化规律[10-12]。该模型工作腔结构比较规范，工作腔容积与夹角成正比，可以直接通过夹角计算出体积，如式(20)所示：

V=Kβ

(20)

式中：V为工作腔容积，mm3；K为转换系数，mm3/rad ；β为工作腔张角，rad。

K代表工作腔内每单位角度内的容积，表征了工作腔的容纳能力，大小与球形泵的结构有关，K可以确定为

K=π/270(R2-r2)3/2

(21)

由空间机构运动、动力分析得工作腔张角：

(22)

4 减振措施

在球形泵工作过程中，惯性力矩和流量脉动是振动产生的主要源头。可以通过减小主轴转速ω和活塞角α，缩小球形转子半径R以降低转动惯量，但会影响泵的容积率，增大加工难度。作者采用成对球形转子泵对称安装的措施，来抵消力矩，并研究对流量脉动的影响。转子陀螺力矩M1比活塞惯性转矩M2大得多，优先减小陀螺力矩。

如图5所示，两泵对称安装，分别建立直角坐标系x1y1z1和x2y2z2。两陀螺力矩矢量方向相反，且大小相等，全部抵消。两惯性转矩大小相同，分别沿O1D1和O2D2方向。经空间矢量分解，合成整体力矩。

(23)

图5 双泵安装示意

4.1 ADAMS振动仿真分析

球形转子泵的力矩和运动都是周期性的，存在周期变化的激振力，导致系统发生受迫振动。ADAMS的Vibration插件可以分析系统在频域的强迫振动响应特性，通过采用虚拟激振器来替代物理实验装置。同时，也可以利用ADAMS/View进行时域的振动分析[13]。设置激振力是正弦扫频信号(文中的转速n=6 000 r/min，频率f=n/60=100 Hz，周期T=1/f=0.01 s)，然后运行分析[13-14]。经过后处理，系统主轴质心点处的位移、加速度的时域响应和频域响应如图6所示。

图6为振动的幅频和相频曲线，3个波动区域即3阶固有频率[12]，工作频率100 Hz位于2阶频率和3阶频率之间，不会因为共振带来重大损害，且振动幅值响应很小，保证了系统运行的稳定性。

图6 频域响应

图7(a)、(b)分别为单泵和双泵振动位移的时域响应，周期为0.01 s的正弦曲线。单泵时的振动位移幅值为0.91 mm，双泵时的振动位移幅值为0.000 7 mm，机械振动大幅度降低。

图7 振动位移响应曲线

4.2 流量曲线分析

对容积V用插值法取得工作室容积的导数，即球形泵的流量变化，可以用来分析流量波动的大小[12]。单泵和双泵合成时的流量曲线如图8所示。

流量脉动的大小可以用波动率表示，波动率δ=(Q最大流量-Q平均流量)/Q平均流量×100%。由图8可以得到单泵的流量波动率约45%，相比之下，双泵组合的波动率只有约 18%，相比降低了60%。

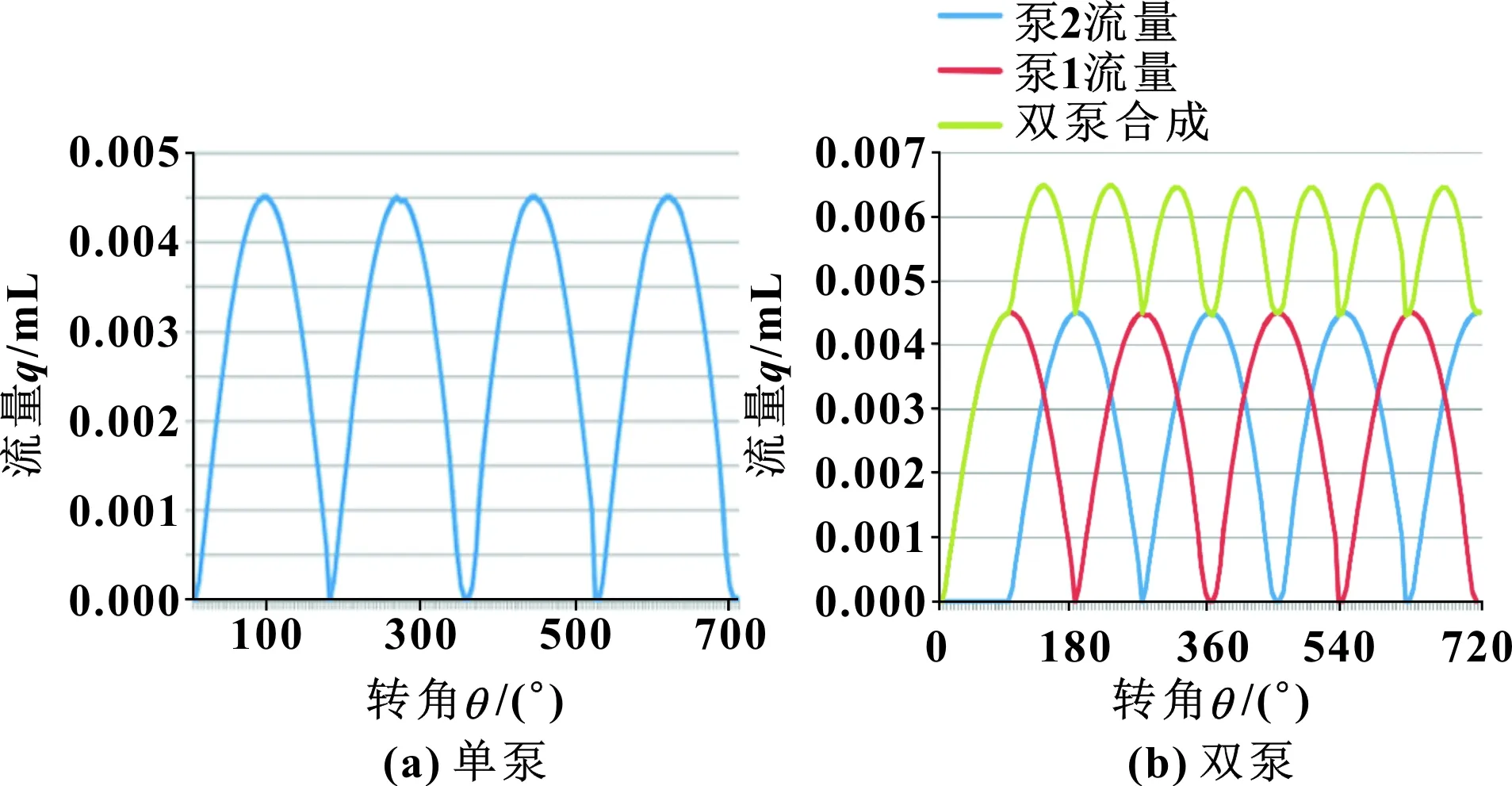
图8 流量波动曲线

通过仿真分析，对比单泵和双泵的机械振动和流量脉动，证明了双泵对机械振动和流量脉动的抑制成效显著。实际工程项目中的多泵采用这种方式，可以很大程度上减小系统振动，提高工作的稳定性。

5 结论

振动会对球形泵造成损伤，并且带来噪声，因此研究泵的机械振动和流量脉动是必须的。对球形泵进行动力学建模，求解旋转盘和活塞的角速度和角加速度，得到活塞的惯性力矩和旋转盘的陀螺力矩。将球形转子的力矩进行合成分析可知，球形泵所受惯性力矩的大小主要取决于旋转盘的陀螺力矩。本文作者在不改变结构参数的前提下，采用多泵减振的方案，抵消力矩和流量脉动。通过ADAMS对球形转子泵进行振动仿真，频域曲线证明了球形泵在激振条件下受迫振动的稳定性。建立球形泵的容积腔变化公式，插值法取得容积变化曲线的导数即球形泵流量，并使用MATLAB生成单泵和双泵的流量曲线。对比单泵和双泵的机械振动位移和流量波动率，双泵状态的振动位移幅值和流量波动率皆大幅度减小。综上结果分析，采用多泵安装既抵消了大部分力矩，又减小了流量脉动，增加球形泵的工作寿命和平顺性。