卷烟烟气成分烟支截留的近似模型

2023-10-12郭吉兆刘瑞红谢复炜张晓兵于宏晓

烟草科技 2023年9期

郭吉兆，刘瑞红，岳勇，刘雨，谢复炜*，尚斌，聂聪，张晓兵，于宏晓*

1. 中国烟草总公司郑州烟草研究院，郑州高新技术产业开发区枫杨街2 号 450001

2. 山东中烟工业有限责任公司技术中心，济南市历下区经十路11888 号 250014

卷烟烟气成分在燃烧锥形成后，经烟丝段和滤嘴段截留，形成主流烟气，因此，烟支的截留作用是影响主流烟气释放量的重要因素。烟草行业已广泛开展了卷烟滤嘴对烟气的截留实验研究［1-3］。高明奇等［4］研究表明丝束规格、压降和通风等滤嘴参数对细支烟烟碱过滤效率均有影响。于涛等［5］考察了醋纤滤嘴对7种酚类成分的过滤效率，表明醋纤对单酚的选择性过滤明显大于苯二酚。胡少东等［6］考察了烟气成分分子量与选择性截留的关系，结果表明，随分子量的减小，烟气成分的选择性截留系数呈升高趋势。在烟丝段截留研究方面，Fordyce 等［7］和Townsend 等［8］考察了不同长度的截留烟丝段对主流烟气烟碱和焦油释放量的影响，表明烟丝段对卷烟烟气也具有非常显著的截留作用。

开展卷烟烟气截留的数学模型研究、定量预测烟气成分的截留率对于卷烟设计具有重要价值。目前，相关研究主要集中在滤嘴对烟气气溶胶颗粒的过滤方面［9-11］，基于纤维材料对气溶胶颗粒的截留机制，建立了烟气气溶胶颗粒过滤的数学模型，实现了对气溶胶颗粒截留率的预测［12］。然而，大多数烟气成分在传输过程中既存在于气溶胶粒相，也存在于气相，颗粒截留模型不能完全解释烟气成分的截留现象，如滤嘴对部分烟气成分的选择性过滤作用［13］。因此，本研究中从烟气的传输机制出发，基于不同的截留过程假设，推导出了卷烟烟气成分烟支截留的数学模型，旨在深入掌握烟支对烟气成分的截留规律，为卷烟的数字化设计提供技术支撑。

1 模型建立

基于对传输过程烟气成分存在形态、不同存在形态间的转化等方面的不同假设，建立了3种烟气成分烟支截留的数学模型。

1.1 模型1

假设初始烟气在燃烧锥产生后，瞬间冷却形成气溶胶，烟气成分x的一部分进入气溶胶颗粒相（以下简称粒相），剩余部分以气态形式仍存在于气相；烟气在向嘴端传输过程中，气溶胶颗粒和气相成分同时被烟丝截留，气相成分不再被气溶胶颗粒捕获，截留机制见图1。其中，N总为燃烧锥初始产生的x的分子数，Nv代表气相中x 的分子数，Na代表粒相中x的分子数，Nd代表沉积在烟丝上的x的分子数。

图1 模型1的烟气截留机制示意图Fig.1 Schematic diagram of smoke retention mechanism for Model 1

进一步假设单位长度烟丝段对气相和粒相烟气成分的截留量分别与进入该段的气相成分量和粒相成分量呈正比，即截留过程符合一级动力学过程，其截留系数分别为k1和k2，可得截留过程的微分模型方程（1）～（3），其中，L为截留烟丝段长度（mm）。

设初始气溶胶形成时，烟气成分x进入气溶胶粒相的比例为a，留在气相的比例则为1-a。可得模型的初始条件：L=0时，NvL=0=（1-a）N总，NaL=0=aN总，NdL=0=0。

由方程（1）和初始条件可得：

由方程（2）和初始条件可得：

由方程（3）～（5）可得：

将初始条件代入公式（6），得C1=N总，故

长度为L的烟丝段对烟气成分x的截留率：

故，烟气成分x经过长度为L的烟丝段后的穿透率为

1.2 模型2

假设卷烟烟气在燃烧锥产生后，烟气中沸点较低的成分x并非瞬间进入粒相和气相，而是在传输过程中随着烟气进一步冷却逐渐进入气溶胶粒相；且烟气传输过程中，气溶胶颗粒和气相成分同时被烟丝截留，截留机制见图2。

图2 模型2的烟气截留机制示意图Fig.2 Schematic diagram of smoke retention mechanism for Model 2

同样，设烟丝段对气溶胶颗粒和气相成分的截留以及气相成分向粒相的转移均符合一级动力学过程，其截留和转移系数分别为k1、k2和k3。可得截留过程的微分模型方程（10）～（12）：

根据假设，模型2的初始条件为L=0时

由物质守恒原理可得Na=N总-Nv-Nd，代入方程（12）可得：

由方程（10）和初始条件可得：

将公式（14）代入方程（13），得：

解该微分方程，得解析解：

其中，C2为常数，将初始条件代入，可得：

代入公式（16），两边均除以N总，得到长度为L的烟丝段对烟气成分x的截留率：

故对应的穿透率为

1.3 模型3

假设卷烟烟气在燃烧锥产生后，瞬间冷却形成气溶胶，烟气成分x 进入气溶胶粒相的比例为a，留在气相的比例则为1-a；在传输过程中，气相中的x可进一步进入到粒相；烟气传输过程中，气溶胶粒相和气相成分同时被烟丝截留，截留机制见图3。

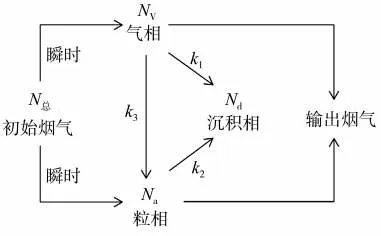
图3 模型3的烟气截留机制示意图Fig.3 Schematic diagram of smoke retention mechanism for Model 3

从假设条件可知，该截留过程的微分模型与模型2相同，但两个模型的初始条件不同。模型3的初始条件为L=0时，NvL=0=（1-a）N总，NaL=0=aN总，NdL=0=0。

由方程（10）和初始条件可得：

将公式（20）代入方程（13），得：

解该微分方程，得解析解：

将初始条件代入到公式（22），得：

将其代入公式（22），两边再均除以N总，得到长度为L的烟丝段对烟气成分x的截留率：

故穿透率为

2 结果与讨论

2.1 3种截留模型比较

比较3 种截留机制下烟气成分的截留率公式（8）、（18）和（24），可以看出，3 种模型的截留率均为双指数函数，其共同的形式为

进一步观察可发现，公式（8）、（18）和（24）中的两个指数系数和均为1，即A+B=1。3 种模型的kB均为粒相截留系数k2。对于模型1，kA=k1，即气相截留系数；对于模型2和模型3，kA=k1+k3，即气相截留系数k1与气相向粒相的转化系数k3之和，因此，kA可统称为气相衰减系数。公式（8）的两个指数项分别代表成分x气相穿透量和粒相穿透量占x产生量的比例，公式（18）和（24）的两个指数项并没有明确的物理意义。

从模型的假设机制看，模型1和模型2均可用模型3参数极端取值进行描述。当模型3的假设中，初始气溶胶形成时烟气成分x进入气溶胶粒相的成分比例a为0 时，其假设机制与模型2 相同。当模型3的假设中，传输过程气相中x进入到粒相可忽略，其假设机制与模型1 相同。从截留率模型公式（8）、（18）和（24）中也可以看出，当公式（24）中a=0 时，其可转化为公式（18）；当k3=0 时，其可转化为公式（8）。因此，模型3可被称为通用模型。

烟气传输时烟支不同位置存在温度差异，烟气成分的冷凝、吸附和颗粒过滤等多种过程均不同程度受温度的影响，3种模型的建立未考虑烟支内温度分布的影响，为近似的简化模型。

2.2 烟丝段截留数据拟合

杜有美等［14］将抽吸1 口后的卷烟烟蒂分切成多个小段，测定了每段烟气成分的截留量，数据分析显示烟丝段对烟气成分的截留作用不能用粒相截留的一级动力学模型描述，作者将原因归于烟气成分的截留同时包括粒相截留和气相截留。采用公式（26）对文献［14］中32种烟气成分的烟丝段截留数据进行拟合，取粒相截留系数kB=0.003 9 mm-1［15］。表1为32种成分截留数据拟合而得的模型参数和相关系数。可以看出，除了对二甲苯外，31种成分的模型拟合相关系数均达到0.95 以上。将糠醛和苯酚等6 种成分的拟合结果作图，如图4所示。可以看出，公式（26）可以较好地拟合糠醛和苯酚等成分在烟丝段的截留数据。这一结果表明，将烟气成分的烟丝段截留区分为气相和粒相的共同截留是合理的，推导出的双指数模型可以用于描述烟丝段对烟气成分的截留。

表1 烟气成分烟丝段截留数据［14］模型拟合结果①Tab.1 Fitting results of retention data［14］of smoke components by tobacco rod

图4 烟气成分烟丝段截留数据［14］的模型拟合曲线Fig.4 Model fitting curves of retention data［14］of smoke components by tobacco rod

2.3 滤嘴截留数据拟合

进入滤嘴的烟气成分也可能同时存在于气相和粒相，且气相和粒相成分均可分别被滤嘴截留，滤嘴内气相成分也可以向粒相转化，滤嘴对烟气成分的截留也符合模型假设条件，因此，这些模型应该也可以用于滤嘴对烟气成分的截留描述。费婷等［16］将卷烟抽吸后的滤嘴分切为多个小段，测定了每段滤嘴中6种酚类化合物的截留量，获得了不同滤嘴长度的截留率。采用公式（26）对滤嘴截留数据进行拟合，取滤嘴的粒相截留系数kB=0.025 mm-1［17］，拟合结果见表2。6 种成分的模型拟合相关系数均达0.95 以上，验证了双指数模型可以用于描述滤嘴对烟气成分的截留。

表2 烟气成分滤嘴截留数据［16］模型拟合结果①Tab.2 Fitting results of retention data［16］of smoke components by filter

2.4 滤嘴选择性过滤

滤嘴对某一成分的过滤效率大于对总粒相物的过滤效率，就认为滤嘴对该成分具有选择性过滤作用［18］。假设滤嘴对总粒相物的截留率近似等于其对气溶胶粒相的截留率，令公式（8）中a=1，可得总粒相物截留率（RTPM）的计算公式：

通过比较总粒相物和烟气成分x的截留率大小，即判断式（28）是否成立，可判断滤嘴是否对x具有选择性过滤作用。

对公式（28）进行化简，可得

也就是说，只要滤嘴对烟气成分x的气相截留系数与气相向粒相的转化系数之和大于粒相截留系数，则滤嘴对x具有选择性过滤作用。当气相向粒相的转化可忽略，即k3=0时，公式（29）表示滤嘴对烟气成分x的气相截留系数大于粒相截留系数，即可满足选择性过滤条件。这一推论是显而易见的，因为成分x分布在气相和粒相，烟气气溶胶粒相是作为整体被截留的，x 粒相部分的截留率与总粒相物相同，只要其气相部分的截留率大于粒相的截留率，该化合物总的截留率即大于总粒相物的截留率，表现为选择性过滤。

根据选择性过滤系数Sx定义［18］，结合公式（24）和（27）可得选择性过滤系数与模型参数之间的关系。

公式（30）可以用于计算成分x 的选择性过滤系数。可以看出，选择性过滤系数Sx与模型参数a、k1、k2、k3和截留长度L均相关。定性地，如果有k1+k3>k2，当气相比例1-a增加时，化合物的选择性过滤系数Sx增加；当k1增加时，Sx增大；当k2增加时，Sx减小；当L增加时，Sx也增加。一般认为，如果滤嘴对一种烟气成分存在选择性过滤，进入滤嘴时该成分应该有相当比例存在于气相，而且滤嘴材料对该成分有亲和性［19］，这两个条件分别对应于模型中气相比例1-a较大、k1较大，与从公式（30）得出的定性结论一致。

2.5 滤嘴分段过滤效率差异

费婷等［16］将卷烟抽吸后的滤嘴分切为多个小段，测定了每小段滤嘴中苯酚的截留量，计算了不同段单位长度滤嘴的截留率，发现靠近烟丝端的滤嘴对苯酚的单位长度截留率高于嘴端滤嘴。可用截留率公式（24）对该现象进行解释。

对公式（24）进行整理，可得：

对于同一滤嘴的各等长度小段，公式（31）中L、k1、k2、k3均相同，则右端前3项为相同值，不同小段的截留率差异取决于第4项值的大小。由于醋纤滤嘴对苯酚具有选择性过滤作用，根据公式（29），k1+k3>k2成立，如果进一步有k1>k2，则公式（31）右端第4项小于零；k1+k3>k2，也意味着气相损失比粒相损失快，靠近烟丝端的滤嘴小段遇到的烟气中x气相比例大于靠近嘴端滤嘴小段遇到的烟气，即随着烟气向嘴端传输，粒相比例a逐渐增加。由于公式（31）中的第4项为负值，a越大，其值越小，因此，同一滤嘴的等长度小段越靠近嘴端，其截留率Rx越小。