局部相位量化在模糊图像识别中的研究进展

刘靖丹,逯 洋,王 淳

(吉林师范大学 数学与计算机学院,吉林 四平 136000)

图像处理技术是利用计算机处理图像来进行科学研究的一门新兴科学。图像处理技术[1]的研究内容十分广泛,包括图像处理的基础,图像处理的研究方法等。图像处理技术的主要内容之一是图像识别。图像识别在图像采集过程中容易受到干扰(如尺度[2]、光照[3]或噪声[4]等),使得这项工作具有极大的挑战性,在其领域中一个较少被研究的性质是模糊[5-6]。环境中运动和大气湍流、低质量的图像系统很可能会产生图像的模糊不清。模糊图像会使图像效果恶化,对图像数据的收集造成障碍。所以,模糊图像特征辨识的方法有着重大研究价值,已成为有关学者探讨的焦点问题而受到了普遍重视。对此,2008年Ville Ojansivu[7]提出了一种用于纹理描述的模糊不敏感纹理分类方法,称为局部相位量化(LPQ)。该方法已经被证明比LBP算子[8-10]对模糊的容忍度更高。之后Timo Ahonen[11]将此方法引用到模糊人脸识别领域,大大提高了人脸识别效率,同时提高了图像处理的效率。后来LPQ算法在人脸识别领域中被不断改进,在局部特征提取方面取得了很好的效果,获得了很大的成功。LPQ算法也被应用于其他领域,如手势识别、面部识别和掌纹识别等。因此,有必要对该方法的相关研究成果进行全面的综述和讨论。

本文系统综述了局部相位量化方法在处理模糊图像上的研究进展,进一步深入研究局部相位量化并以求为拓展其应用领域奠定基础。本文从介绍LPQ算子的起源开始,阐述了不同实验研究的动机、原理、优缺点,揭示了各种方法之间的差异和联系,最后思考了该方法的发展方向。

1 模糊不变的局部相位量化方法

模糊不变的局部相位量化方法的优势有以下五点:(1)在处理图像时不需要加入特征点;(2)不需要对图像进行分类;(3)不需要新建模型,对已有的旧模型进行训练,计算结果与模型的性能指标保持一致;(4)可以作为快速处理的对象和模型;(5)在处理过程中具有可扩展性。在LPQ方法中,可以直接在计算机上用LPQ方法对图像进行分类。

基于二维离散傅里叶变换[12](DFT)的LPQ算子,使用短期傅里叶变换(Short-Term Fourier Transform,STFT)计算像素点局部邻域内的相位信息。

1.1 离散傅里叶变换(DFT)

在数字图像处理中,模糊图像g(x)可以通过原始图像f(x)和点扩散函数(PSF)卷积构成,其表达式如下:

g(x)=(f*h)(x)

(1)

将其进行傅里叶变换转变到频域,则式(1)转化为:

G(u)=F(u)·H(u)

(2)

其中G(u),F(u)和H(u)分别是g(x)、f(x)和h(x)进行离散傅里叶变换(DFT)后的结果。可以将(2)式的幅值和相部分开,得到如下相位关系表达式:

|G(u)|=|F(u)|·|H(u)|和

∠G(u)=∠F(u)+∠H(u)

(3)

假设模糊点扩散函数h(x)是中心对称的,即h(x)=h(-x),如果傅里叶变换总是得到实值,那么它的相位只是一个二值函数,如式(4)所示:

对于规则的点扩散函数,使得当所有H(u)≥0时都有:

∠G(u)=∠F(u)

(5)

这一关系就为模糊不变特征提取奠定了理论基础。

1.2 短期傅里叶变换(STFT)

STFT是由(6)式定义的f(x)的每个像素位置x处的M·M邻域Nx上计算的,其中Wu是频率u的二维DFT的基向量,fx是另一个包含来自Nx的所有M2图像样本的向量。

可以看出,实现STFT的一种有效方法是对所有u使用二维卷积。

4个频点u1=[a,0]T,u2=[0,a]T,u3=[a,a]T,u4=[a,-a]T通过局部傅立叶系数计算,a表示范围很小,a=1/M。每个像素位置通过向量表示,如式(7)所示:

Fx=[F(u1,x),F(u2,x),F(u3,x),F(u4,x)]

(7)

傅里叶相位系数可使用各部分的实数和虚数的符号来表达,如式(8)所示。

gj是向量G(x)=[Re(Fx),Im(Fx)]的第j个部分。然后qj对其进行二进制编码,如式(9)所示。

LPQ(x)表示窗口尺寸为M×M的算法,图1中是窗口为5×5的LPQ算法实例。

图1 LPQ算法

2 LPQ算子的研究概况

2.1 针对灰度图像的LPQ算子及变体

LPQ算法大多针对灰度图像,研究内容大多是以人脸和纹理图像为研究对象来进行归纳。不同的实验研究使用了不同的数据集,包括Outex、YALE、AR和ORL等。

2.2 对单一图像模糊不敏感纹理分类方面的研究

Ville Ojansivu等人[7]提出了一种用于纹理描述的模糊不敏感纹理分类方法,称为局部相位量化。其研究重点是模糊不敏感的纹理分类,相比之下,LPQ比LBP对模糊的容忍度更高。Timo Ahonen等人[11]将LPQ算子用于模糊人脸的识别,通过向LPQ添加一个去相关来达到要求。通过对不同区域直方图的连接,完成人脸的全局描述,提高了算法识别率。朱长水等人[13]提出将局部二值模式和LPQ进行融合的人脸识别方法,具体算法如图2所示。该方法比较直方图的相似性,根据最近邻原则进行识别,提高了算法的鲁棒性。

图2 LBP/LPQ算法

Xiao等人[14]提出局部相位量化加(LPQ+),将LPQ嵌入到Fisher向量(FV)中,利用FV增强模糊图像识别性能,并且LPQ+直接量化STFT的局部相位。该方法有更强的局部模式表征能力,可以提高模糊图像的识别性能。Zhu等人[15]对LPQ+进行改进,提出一种判别模糊不敏感的纹理描述符,称为局部相位量化加加(LPQ++)。该方法是在STFT产生的归一化模糊不敏感特征映射之间,建立空间信道相互作用以增强描述能力,同时保持对模糊的不敏感。

陈晓文等人[16]提出用高斯拉普拉斯边缘检测和局部相位量化增强结合的模糊图像识别算法MrELPQ和MsLoG(Multi-resolution ELPQ and Multi-scale LoG)。通过正负量化和幅值量化的操作,得到具有互补符号特征的ELPQ_S和幅值特征的ELPQ_M,将特征直方图进行串联,得到增强的局部相位量化模式,该算法增强了模糊的鲁棒性,并且具有更好的识别性能。

Ojansivu等人是最早专门针对模糊图像进行研究的,后来的研究者都是以他们的研究为依据不断改进,以达到更好的效果。这是当时最具代表性和最具影响力的研究成果,也为识别模糊图像打开了新篇章。Ahonen是首个将LPQ方法应用于人脸识别领域的,研究成果是LPQ算法应用人脸识别领域的开端。他的实验巧妙地在LPQ上使用去相关来进行改进算法,最后发现LPQ不仅可以很好地处理模糊,而且可以很好地处理现实图像中的其他干扰,实验更加验证了LPQ在识别模糊图像上的优越性。朱长水基于Ahonen的实验进行画面分块,发现这个技术还存在着一定的局限,需要重复试验计算以确定最合适的大小来达到较好的识别率。以上实验都是针对简单的模糊图像,遇到复杂的图像时,只通过LPQ单一方法不容易得出好的结果。Xiao等人创新了人脸识别方法,借助FV在BoW模型中获得新的模糊图像,改变LPQ对STFT操作过程,从而获得更强的局部表征能力。同时针对多种不同数据集进行试验,做了大量改进工作,实验结果很好,但主要问题是对不同纹理的辨别能力没有得到充分利用。Zhu等人发现LPQ+忽略了STFT特征图中不同频率点之间的空间和通道相关性,可能导致某些具有内在价值的纹理线索被忽略,所以进行再次改进,过程中发现归一化STFT系数特征图之间的通道梯度可以从本质上帮助区分特定图像中的边缘和平坦区域,这对于模糊纹理的识别是至关重要的。

2.3 结合旋转变化和图像模糊不敏感纹理分类方面的研究

图像去模糊工作复杂且困难,为预防图像处理工作受到其他外部因素的影响,Ville Ojansivu等人[17]提出一种新的模糊和旋转不敏感纹理描述子,称为旋转不变局部相位量化(RILPQ)方法,是对模糊不敏感的LPQ纹理描述子进行旋转不变的扩展。通过估计局部特征方向并计算有向二值描述子,使其在旋转模式下表现更好。

2.4 结合尺度变化和图像模糊不敏感纹理分类方面的研究

图像处理过程容易受到尺度变化的影响,朱长水等人[18]提出尺度不变特征转换(SIFT)和LPQ结合的人脸图像识别方法。SIFT算法检测并获取所有人脸图像特征点,统计所有特征点邻域的LPQ数据并显示成直方图序列,该方法是计算特征点邻域距离比得到的,在尺度、旋转、明暗等方面存在着一定的鲁棒优势,具有较好的识别效果,能有效降低面部信息的维度。提取的特征点主要集中在眼睛、鼻子和嘴巴上,这些点与面部特征相匹配,可以实现快速识别。以上基于LPQ方法的优缺点及其工作原理,如表1所示。

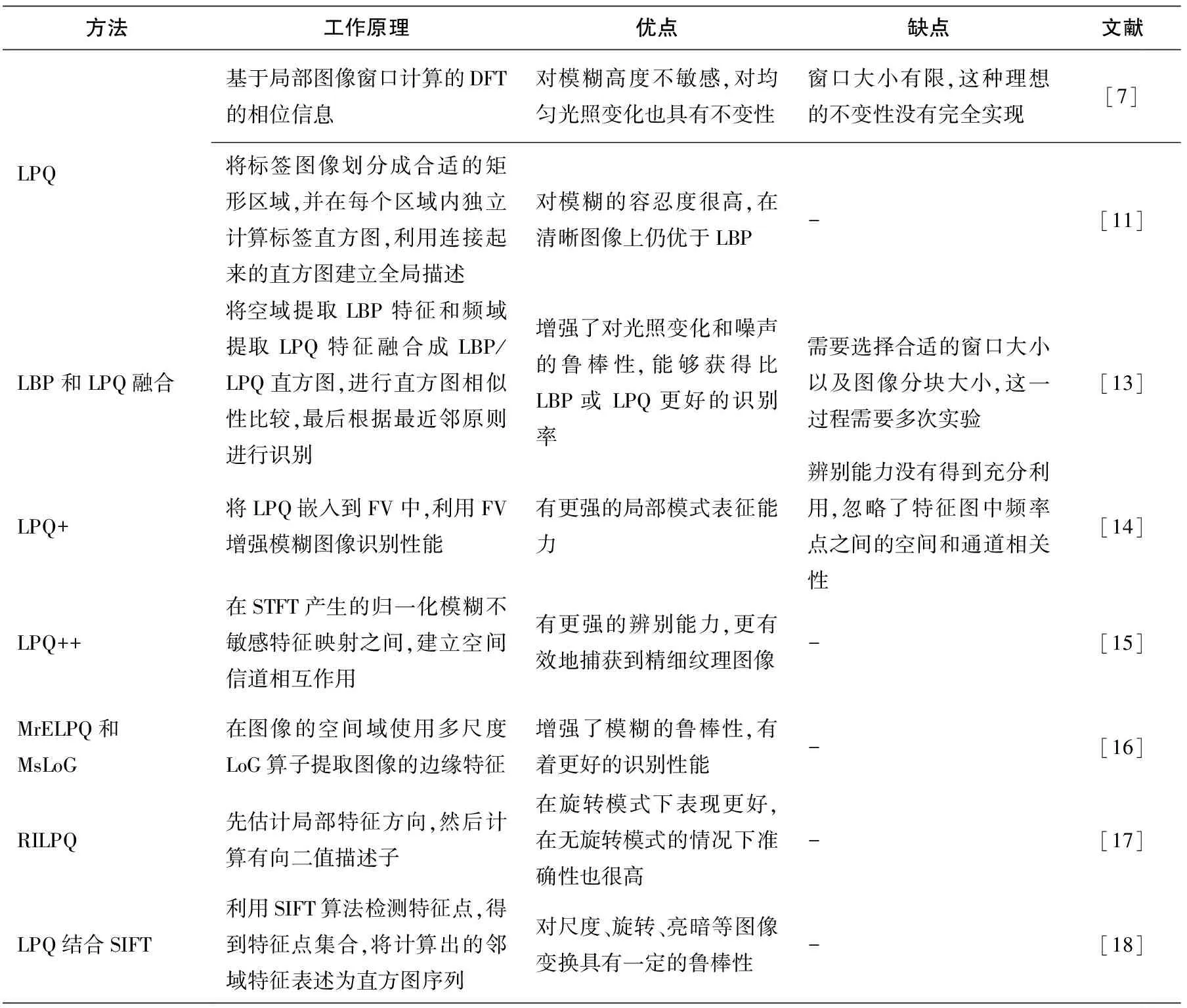
表1 基于LPQ方法的优缺点及其工作原理

2.5 针对彩色图像的LPQ算子

上述实验数据集大多是对灰度图像进行识别,而现如今获取到的人脸图像多为彩色图像,一些研究者会将彩色图像转化为灰度图像,这也将大大增加工作量,更加费时费力。想要实现符合现代的人脸识别技术,Matteo Pedone等人[19]提出针对处理彩色图像的LPQ描述符的扩展方法,该方法是利用颜色值的多向量表示得到的,是一种基于克利福德代数的LPQ描述子颜色扩展方法,该方法在模糊和非模糊纹理分类中具有较好的鲁棒性。LPQ描述符仅限于灰度图像,该描述子比灰度描述子和其他颜色纹理描述子具有更高的精度。此外,它的光照不变特性保证了在具有挑战性场景中的卓越性能,而无需用颜色不变算法预处理纹理。该算法也解决了分类的图像可能会经历的辐射失真、噪声和模糊等原因导致的退化。

3 拓展LPQ方法应用领域

上述内容研究领域单一,依据本身对模糊不敏感的独特特征,一些学者将此算子拓展到其他领域,扩大了算法的通用性,以下内容对此进行了列举。

3.1 在掌脉识别中的应用

在手掌静脉识别系统中,因为人类手掌生理构造特点易产生影像模糊,使得识别精度降低。林森等人[20]提出了基于子区域LPQ鲁棒识别问题的方法。通过建立一个LPQ特征提取模型,将掌脉图像分为几个子段,提取并集成每个分区的LPQ特征,最后利用卡方距离匹配识别。该方法具有良好的手掌图像模糊强度,有效提升了手掌静脉识别系统的性能。

3.2 在人耳识别中的应用

现实中获得的人耳图像数据往往具有不同程度的信号退化,最典型的信号衰减类型是模糊和热噪声。为改善这一问题,黄冠等人[21]比较人耳图像识别过程中三种不同的图像识别算法的影响,分别用到方向梯度直方图(HOG)、LPQ和 LBP方法进行实验,经过对比LPQ算法对模糊性有很好的识别能力,LBP算法如图3所示。

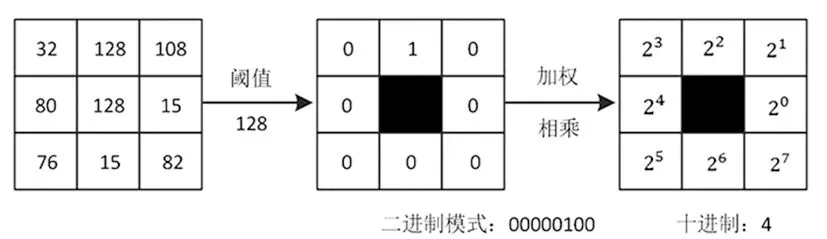
图3 LBP算法

3.3 在车标识别中的应用

贺敏雪等人[22]提出基于抗模糊特征的车标识别方法,以解决标识图像上的图像模糊问题。通过构建标志图像金字塔模型,利用LPQ算法提取车标图像的抗纹理和抗边缘模糊特征,并且使用典型相关分析(CCA)以促进后续的降维和分类。该方法结合两种抗模糊特征,具有较好的识别效果和较强的鲁棒性和抗模糊性。

3.4 在森林火灾图像识别中的应用

为减少森林大火的误报概率和提升火灾报警效率,李巨虎等人[23]提出火焰独特色彩和纹理特征的火焰识别算法,将LBP和LPQ直方图特征融合到了分块中。算法将图像变换到YCbCr颜色空间,根据LBP与LPQ算法提炼所有疑似火灾区的图像与数据,并且利用支持向量机(SVM)识别火焰纹理。该算法提高了识别率,能成功区分红叶林与火焰,可以快速预测火灾。

3.5 在维吾尔文离线手写签名中的应用

为了提高离线手写签名识别的精确性,张淑婧等人[24]提出基于纹理特征的维吾尔文离线签名识别方法。提取多尺度块LBP和LPQ纹理特征,通过随机森林(RF)对图像进行分类识别。该方法对签名识别具有较好的准确性。针对不同实验基于LPQ方法的图像识别效果如表2所示。

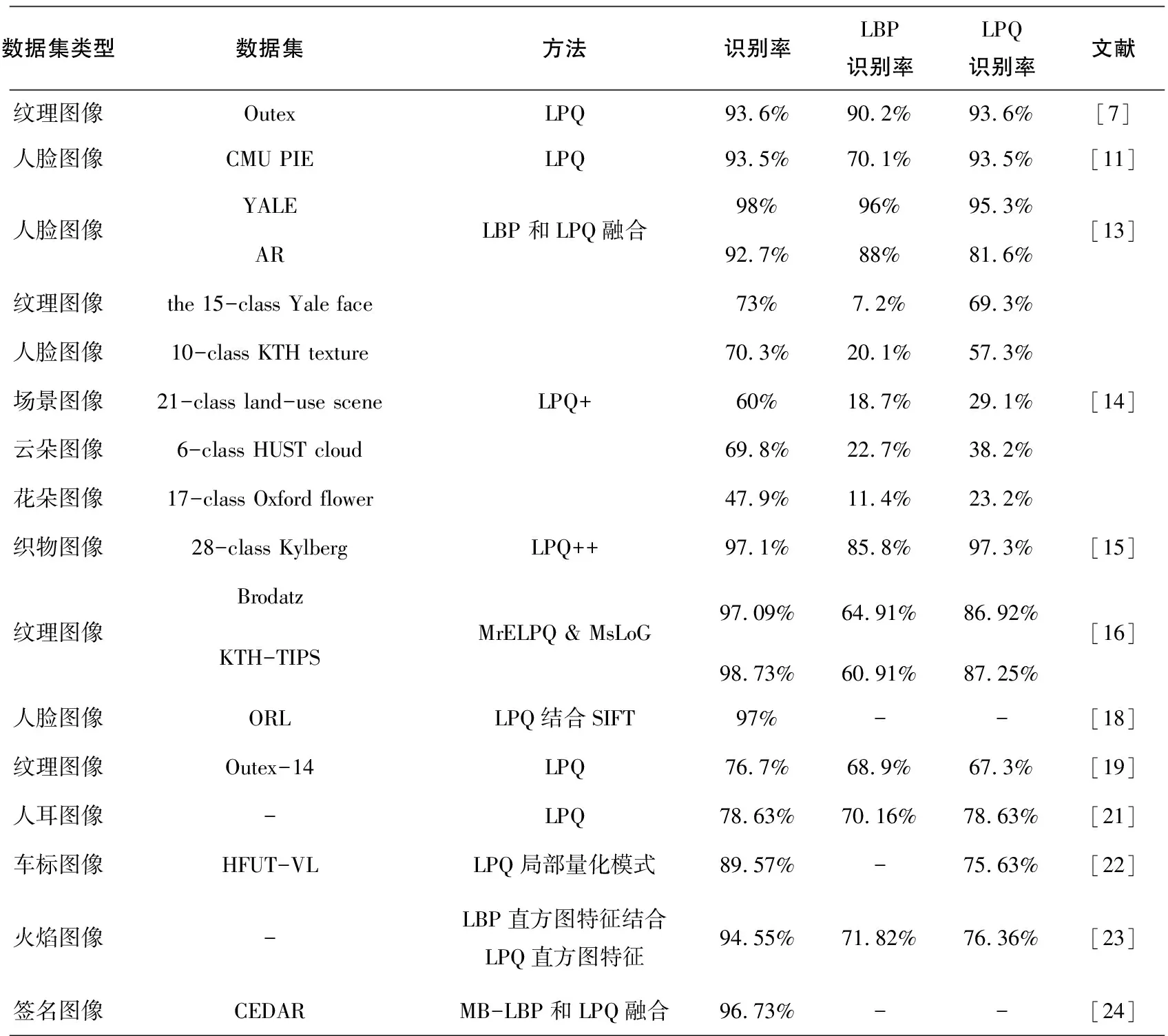
表2 不同实验基于LPQ方法的图像识别效果

4 结语

通过介绍模糊图像基于LPQ方法的研究进展情况,可以看出基于LPQ方法的图像处理是一种有效的方法。可见LPQ算法及其变体在图像处理、计算机视觉领域提供了一类重要的特征提取方法,并且LPQ算法通用性强,不局限于灰度图像,甚至在多个领域图像识别结果中都有着极高识别率。

LPQ方法具有强大的应用价值与广泛的应用前景,对纹理特征提取过程中解决模糊因素影响的研究方法越来越丰富。因此,在实际操作中研究者应该对基于LPQ的图像处理方法进行不断的改进与完善。一方面,可以结合多种影响因素进行纹理特征提取,以获取更全面、准确的特征信息;另一方面,也可以改进现有的相关方法或者寻找更加合适的模糊度量方法,从而提高算法的精度和鲁棒性。这些改进措施可以大幅提升算法的性能,使其在实际应用中表现更加优越。

在研究LPQ这类问题过程中发现,处理模糊图像也能够通过深度学习的方法得到解决。关于深度学习方法来解决图像模糊的问题,后续会进行深入研究并继续扩展LPQ的应用领域,尝试对图像进行分割处理来有效地提取图像信息,从而能够更好地解决模糊图像处理中复杂系统的不确定性的难题。