装配式建筑竖向接缝剪力墙抗震性能研究

张成利 ,刘 峰

(1.连云港开放大学 工程技术学院,江苏 连云港222062;2.辽宁科技学院 资源与土木工程学院,辽宁 本溪 117004)

0 引言

现阶段我国正处于产业结构调整的关键时期,建筑产业化发展可以实现资源的优化配置、改善施工质量和效率,顺应国家可持续发展的战略目标[1-2]。传统的基于钢筋混凝土现浇施工体系存在的经济成本高、施工难度大、施工周期长、质量难以保证等问题逐渐得到重视,而装配式剪力墙建筑结构因房间中不外露梁、柱棱角等而提高了房间的审美效果,因此成为住宅产业化发展的主要结构形式[3-4]。装配式剪力墙在进行相邻墙体的拼接安装时,墙体之间在竖直方向上形成竖向接缝,竖向接缝的稳定性直接影响剪力墙结构的整体性能。装配式建筑的竖向接缝结构主要依靠接合筋抵抗剪力,可以通过解决新旧混凝土界面的抗剪问题来改变接缝性能以提高界面的抗剪承载力[5]。为探究装配式建筑竖向接缝剪力墙结构的抗震效果,设计不同的竖向接缝剪力墙试件进行试验,探究其受力性能,并将其与现浇混凝土的装配式剪力墙结构进行比较。然后构建有限元分析模型对竖向接缝剪力墙的抗震性能进行模拟分析,以期实现对竖向接缝剪力墙的结构分析,不断优化其施工工艺和质量,提高建筑的抗震效果。

1 装配式建筑竖向接缝剪力墙抗震实验设计

1.1 竖向接缝剪力墙的拟静力试验

为研究竖向接缝剪力墙建筑的抗震性能以及在地震等外力作用下竖向接缝的受剪能力,研究设计四种竖向裂缝的剪力墙试件,并对其进行拟静力试验分析。以剪跨比和轴压比为研究参数对其进行实验设计,试件分别定义为SW-1、SW-2、SW-3、SW-4。其中,S表示试件的剪切破坏发生在试件的弯曲破坏之间,W表示预制的剪力墙。所有试件均由上部加载梁、中间墙体以及底部的底梁三部分结构组成,试件端部为边缘构件,大小为 130 mm×130 mm,配筋率为 1.270%[6]。SW-1为弱连接、强墙肢。SW-2为弱连接、强墙肢、锚固板均无翼缘,SW-3 凹口处锚固板上下伸入预制墙,SW-4 竖向接缝与 SW-3 试件结构一致,不同之处在于SW-4试件结构设置为弱连接,依据水平承载力相等原则连接墙肢与墙体结构[7]。竖向接缝剪力墙试件的制作主要分成两个阶段,第一阶段将试件边缘所需的构件纵筋、箍筋以及水平分布筋进行固定,组成盲孔预制墙钢筋模型,对该钢筋模型进行混凝土浇筑,当混凝土达到所需要的强度后取出钢筋模型,完成盲孔预制墙的制作。第二阶段即制作剪力墙的整体试件,将预制的钢筋模型插入底梁钢筋笼的指定位置[8],完成浇筑混凝土,当混凝土达到预定强度后对加载梁钢筋笼、支设模板等进行固定。最后对纵向孔洞、横向的孔洞以及加载梁混凝土进行浇筑,完成试验试件的制作。竖向接缝剪力墙试件均使用C30混凝土材料,试验前对试件的受力性能进行测试,预制混凝土试件轴心平均抗压强度如公式(1)所示。

fc=0.76(δpfcup,m+δcfcuc,m)

(1)

公式(1)中:δp表示剪力墙试件预制混凝土的体积占比;δc表示剪力墙试件后浇混凝土的占比;fcup,m表示预制混凝土试件抗压强度的平均值;fcuc,m表示后浇混凝土试件抗压强度的平均值。

在对竖向接缝剪力墙进行加载试验时,利用底梁两侧的压梁以及水平限位装置对剪力墙试件进行固定,试验采用的加载装置是最大加载力为3 000 kN的竖向千斤顶对其施加轴向的压力[9]。为使竖向接缝剪力墙受力均衡,研究在加载梁的上方设置分配钢梁用于荷载分配,试验采用位移加载,拟静力试验的加载条件如图1所示。

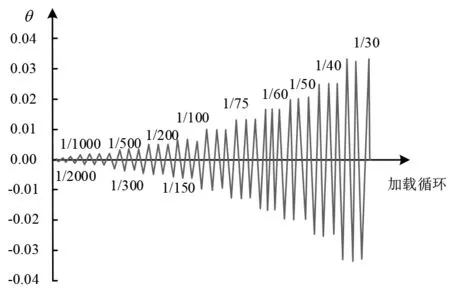
图1 拟静力试验的加载的过程

在正式加载之前,需要对试件进行预加载。一般取竖向荷载的50%左右,水平荷载施加 50 kN,往返一次,观察采集系统是否正常。采集系统正常采集以后,施加竖向荷载。在加载过程中,加载方向为东时定义为正向加载,加载方向为西时定义为负向加载,θ表示加载点的位移角度[10-12]。水平荷载每级增加25 kN,每次循环都要观察试件裂缝。裂纹出现后,试验改用施加水平位移进行控制加载。当荷载加载至峰值力的85%左右或者试件出现破坏以后,整个试验结束。利用载荷传感器以及指针位移测量计对试验载荷、位移等受力变化进行测量。

在对竖向接缝剪力墙结构的抗震性能进行评价时,现有的相对通用的标准是在较小地震发生时,剪力墙结构无任何损坏。在中等强度地震发生时,剪力墙可能出现非结构性的损坏。在大地震发生时,出现结构性和非结构性损坏,但建筑结构不发生倒塌[13]。仅以改变剪力墙结构的承载力来提高抗震性能的方法不适用于大地震,因此,剪力墙结构应当同时具备合适的承载力和屈服后的塑性变形能力才能达到抗震的效果[14]。剪力墙结构的屈服后的塑性变形能力为结构的延性,一般采用位移延性系数衡量钢筋混凝土结构的延性能力。如公式(2)所示。

(2)

公式(2)中:μΔ表示位移的延性系数;Δy表示屈服位移;Δu破坏的位移,在弹性受力条件下,Ke表示剪力墙结构的竖向接缝产生水平单位位移时对应的剪力初始刚度,初始刚度的计算公式如式(3)所示。

(3)

公式(3)中:P表示结构顶部水平集中力;Δ表示水平位移;β为相对刚度,即装配式建筑竖向裂缝剪力墙与整体剪力墙结构初始刚度之间的比值。如公式(4)所示。

(4)

公式(4)中:Ke0表示整体剪力墙的初始刚度,如公式(5)所示。

(5)

公式(5)中:hw表示剪力墙墙体截面而对高度;H表示结构高度;EI表示墙体界面的抗弯刚度。

1.2 装配式建筑竖向接缝剪力墙有限元模拟

在对竖向接缝剪力墙进行拟静力试验外,再使用有限元模拟对其进行数值模拟。研究采用ABAQUS有限元软件对竖向接缝剪力墙的受力性能进行模拟分析。在建立装配式建筑竖向接缝剪力墙的有限元模型之前,需要对剪力墙中所使用的钢混材料的性能进行分析。研究采用的钢筋的屈服点fc=445 MPa,弹性模量Ec=2.0×105MPa,泊松比vs=0.3。由此得到钢筋材料的应力变化关系如图2所示。

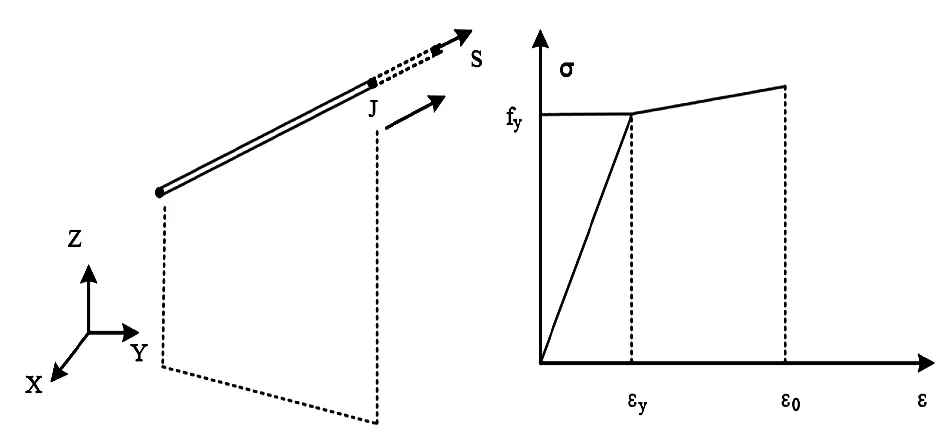
(a)钢筋实体单元示意图 (b)钢筋应力应变关系图2 钢筋材料的应力应变关系

塑性损伤模型是ABAQUS有限元分析模型中的一种混凝土本构关系模型,该模型在充分考虑混凝土材料的自身特征的同时,可以有效地提高计算的精度,对钢筋混凝土墙体的有限元分析时需要考虑非线性问题,通过对模型参数不断进行调整,将误差结果降到最小[15-16]。在定义装配式建筑竖向剪力墙的混凝土弹性行为时,其弹性模量Ec的计算过程如公式(6)所示。

(6)

公式(6)中:fcu表示混凝土材料的抗压强度标准数值,根据混凝土材料的受压以及受拉应力应变来计算其应力和应变,并将其转化为真实的应力和应变。真实应力σtrue如公式(7)所示。

σtrue=σn(1+εn)

(7)

公式(7)中:σn表示名义上的应力值,实际应变如公式(8)所示。

εtrue=ln(1+εn)

(8)

竖向接缝剪力墙的混凝土材料受到不同的外力作用时,对材料的性能影响较大。根据剪力墙受到的外界压力,受压时的损伤因子如公式(9)所示。

(9)

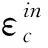
(10)

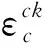
图3 基准试件SPW-5的有限元模型

有限元模型的各个组成部分主要分为混凝土和钢筋类。为保证剪力墙的计算精度, 需对有限元模型进行密度较高的网格划分,划分网格时将加载梁划分单元格长度为80 mm的正六面体,墙体划分单元格长度为50 mm正六面体。模型中各个接触面通过部件之间的相互作用连接在一起。

2 剪力墙竖向接缝结构抗震效果分析

2.1 有限元模拟结果分析

根据装配式建筑竖向裂缝剪力墙的破坏形态,以1个现浇整体剪力墙作为对照试件(SW-5),对试验试件的刚度进行模拟计算,结果如表1所示。从表1来看,试验试件的初始刚度模拟计算值与试验结果相差较大,是由于在实际试验中,受竖向裂缝位移变化的取值方式所影响。在不同纵筋条件下,试件的初始刚度和相对刚度差异明显。剪力墙竖向接缝相对刚度的计算结果与试验结果之比在0.85～1.05范围内,两者的符合程度较高。

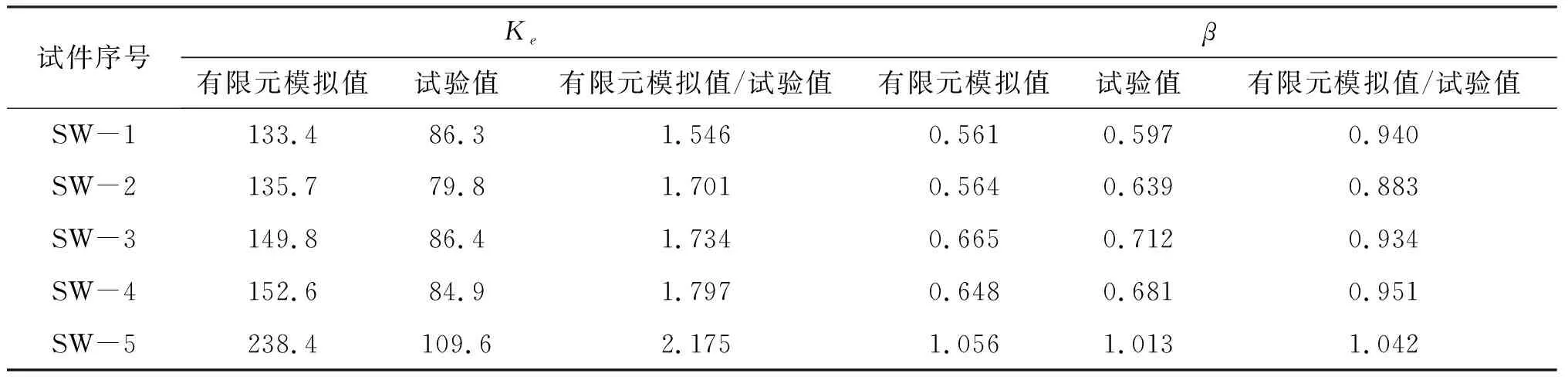
表1 各个试验试件的初始刚度、相对刚度值比较

采用有限元方法对竖向接缝不同部位的受力进行分析。以基准试件为例,对基准试件的顶点处的位移以及内力变化进行计算,结果如图4所示。从图4(a)来看,在距离基地相对高度高于0.8 m时,竖向接缝受到的剪力的实际结果略低于有限元分析结果。同时在相对高度低于0.3 m时,实际的剪力大小也略低于有限元分析结果,但整体的剪力变化趋势一致。从图4(b)来看,竖向接缝的墙肢轴力的实际大小与有限元分析结果高度吻合。在图4(c)中,墙肢弯矩的实际受力大小与有限元分析结果的变化趋势一致,但是有限元分析结果呈现的墙肢弯矩的变化范围略大于实际变化范围。在图4(d)中,墙肢剪力的实际受力大小与有限元分析结果高度一致。因此,整体来看,有限元方法的计算结果与试验结果基本吻合。

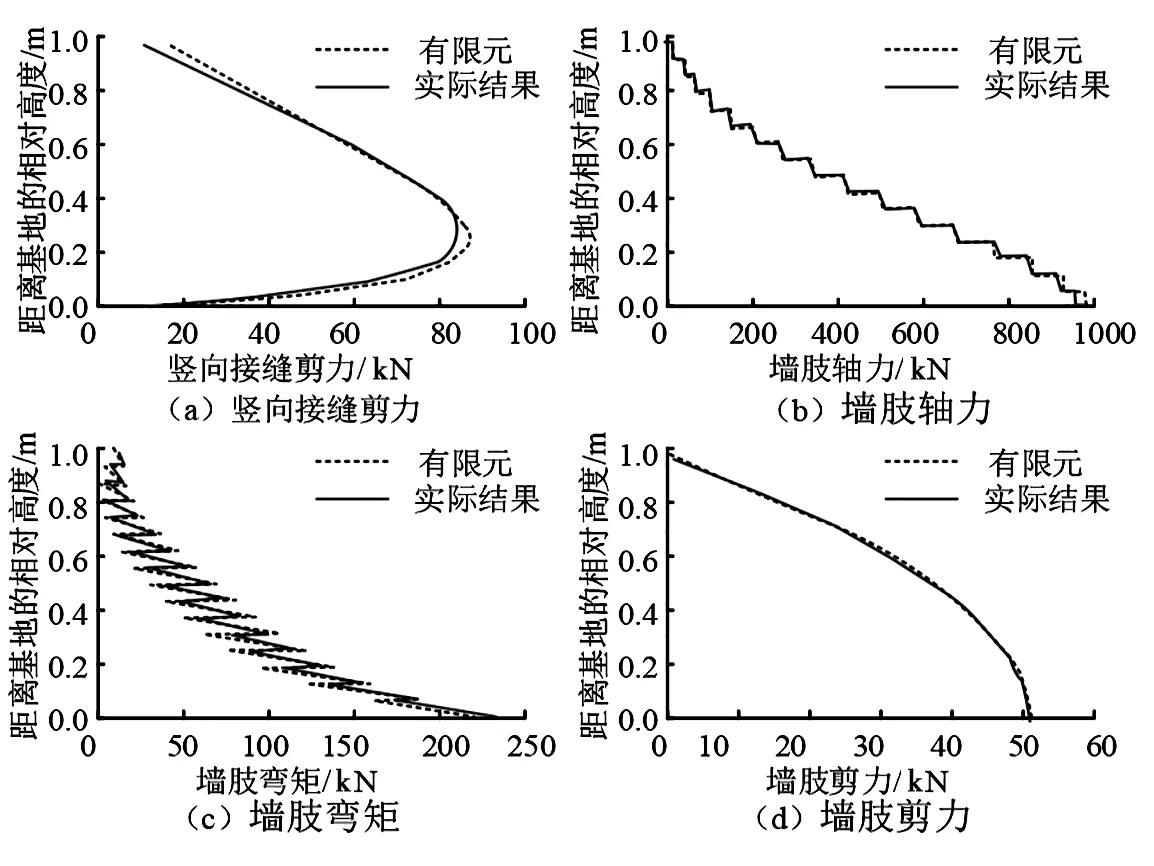
图4 模型的内力比较

2.2 竖向接缝剪力墙抗震性能分析

为验证竖向接缝剪力墙抗震性能,研究构建了4种竖向接缝装配式剪力墙试件,并对试件的破坏形态、荷载-位移曲线、承载力等主要性能进行分析。同时以 1 个现浇整体剪力墙作为对照试件。试件的骨架曲线是荷载-位移曲线在循环过程中滞回曲线达到最大值的外包曲线,可用于表示剪力墙竖向接缝结构发生形变之后的荷载-位移变化,反映剪力墙结构的开裂以及延性强度等变化,不同试件的骨架曲线变化如图5所示。从图5来看,根据各个试件的整体骨架曲线变化来看,所有试件在开裂之前均处于弹性状态。在开裂到屈服强度之前,试件初始刚度差异较小,开裂到屈服强度时,试件整体刚度出现差异,但差异相对较小,在达到屈服强度之后,试件的刚度逐渐降低,荷载水平开始稳定增加。当试件的荷载水平达到最大值之后,承载力开始缓慢下降。其中,SW-1、SW-2和SW-3的骨架曲线重合度较高,SW-1的荷载能力高于SW-2和SW-3,但是,SW-3的极限变形能力高于SW-1 ,即在凹口处深入剪力墙,提高墙肢的完整性可以有效地改变装配式剪力墙的极限变形能力。与SW-4相比,装配式剪力墙的荷载水平显著降低,说明纵筋率对竖向剪力墙结构的稳定性有直接影响。

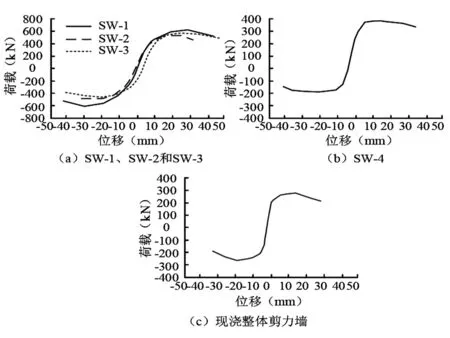
图5 不同试件的骨架曲线比较

研究对竖向裂缝剪力墙试件的竖向钢筋应变分布进行分析。以试件的正向加载为例,分别选择竖向裂缝剪力墙的开裂点、位移控制的屈服点、2倍位移的屈服点以及剪力墙受破坏情况下水平承载力的峰值点的应变大小进行分析,分析结果如图6所示。在图6中,不同试件开裂点的应变均不显著,SW-4 的开裂点应变在截面位置500 mm处发生轻微变化。屈服点的应变同样无显著变化,仅在SW-4中截面位置500 mm处急剧增加到16 000×10-6kN。2倍位移的屈服点应变随着截面位置的变化发生不同程度的改变。SW-1中,2倍位移的屈服点的最大应变20 000×10-6kN。SW-2中,2倍位移的屈服点的最大应变16 000×10-6kN。SW-3中, 2倍位移的屈服点的最大应变18 000×10-6kN。SW-4中, 2倍位移的屈服点的最大应变17 000×10-6kN。在屈服后,试件的竖向分布筋应变明显,竖向裂缝剪力墙墙底发生内力重新分布现象。

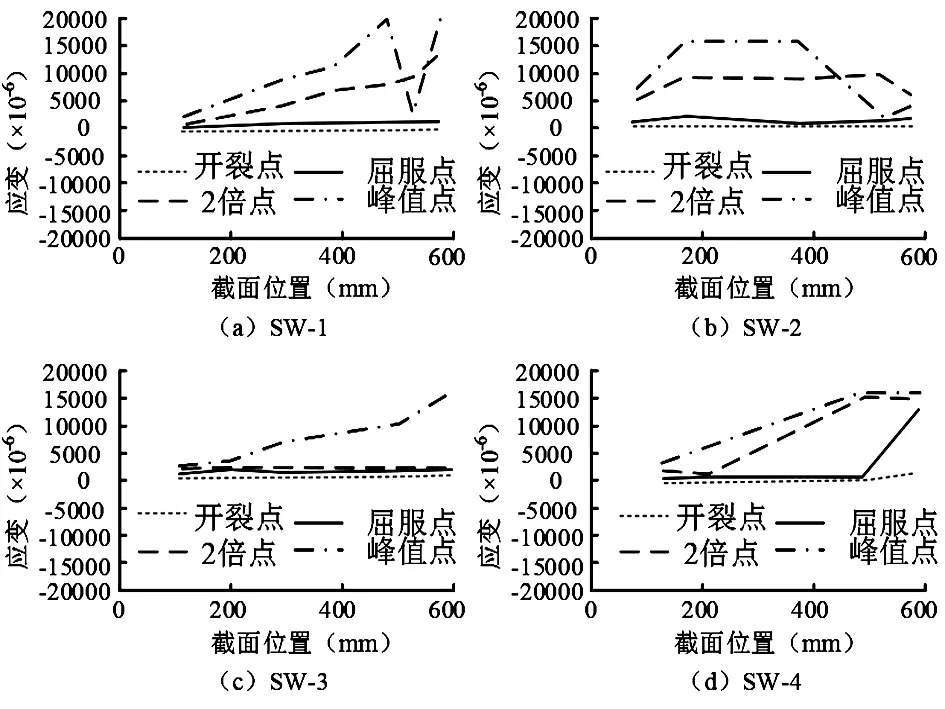
图6 竖向裂缝剪力墙墙底截面钢筋应力分布

3 结论

通过对装配式建筑技术不断地深入探索和研究,使得相关的建筑施工技术越来越成熟,而剪力墙的抗震性能是施工过程中需要重点考虑的问题之一。为深入探究装配式建筑竖向接缝剪力墙的抗震性能。研究设计4种不同条件的竖向接缝剪力墙试件,对其进行拟静力试验来探究竖向接缝剪力墙的抗震效果。在此基础上,构建基于有限元模型的竖向接缝剪力墙的受力性能参数分析。试验结果显示,SW-1、SW-2和SW-3的骨架曲线重合度较高。SW-1的荷载能力高于SW-2和SW-3。但是,SW-3的极限变形能力高于SW-1 ,即在凹口处锚固板深入预制剪力墙中,提高墙肢的完整性可以有效地改变装配式剪力墙的极限变形能力。与SW-4相比,装配式剪力墙的荷载水平显著降低,说明纵筋率对竖向剪力墙结构的稳定性有直接影响。屈服点的应变同样无显著变化,仅在SW-4中截面位置500 mm处急剧增加到16 000×10-6kN。2倍位移的屈服点应变随着截面位置的变化发生不同程度的改变。由此说明,凹口处锚固板上下伸入预制墙能改善试件的极限变形能力及延性能力。与相同配筋率的现浇整体剪力墙相比,竖向接缝的装配式剪力墙的初始刚度有所减小,刚度退化规律基本一致,承载力基本相同,极限变形能力、延性性能普遍较好。即装配式建筑竖向接缝剪力墙的受力效果较好,有较好的抗震效果。但是,研究仍存在不足。针对不同宽高比条件下的竖向接缝剪力墙的受力变化没有进行试验。在后续研究中,需要对该内容进行深入研究。