2023年高考甲卷理数解析几何大题的深入探究

安徽省合肥市肥东县城关中学(231600) 王东海

直线与圆锥曲线的位置关系问题一直是高考的热点和难点,在这类考题的命题中往往都是探求一些特殊结论,这些结论看似特殊,实则往往都具有普遍性. 我们在解答考题后要深入拓展到一般情况,还要注意探寻其它圆锥曲线的对偶性质. 下面以2023 年高考全国甲卷第20 题的圆锥曲线试题的探究为例进行说明.

1 真题呈现

题目 (2023 年甲卷理数第20 题)已知直线x -2y+ 1 = 0 与抛物线C:y2= 2px(p>0)交于A,B两点,且

(1)求p;

(2) 设C的焦点为F,M,N为C上两点,面积的最小值.

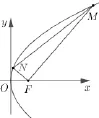
图1

易得第(1)问y2= 4x. 第(2)问求面积最值可用点参法、焦半径公式、极坐标方程解答,得试题平中见奇,内涵丰富,是具有研究性学习价值的好题.

2 一般性探究

细品解题过程,笔者发现结论值得探究. 能否将试题第(2)问中的特殊抛物线推广至一般的抛物线? 基于以上思考,可以得到以下一般性结论:

结论1已知C:y2= 2px(p>0)的焦点为F,M,N为C上两点,则∆MNF面积的最小值为

证明以F点为极点, 以x轴正向为极轴方向建立极坐标系, 则y2= 2px极坐标方程为:设故而

将定点F推广成x轴上其它定点,比如坐标原点,则可得以下结论:

结论2已知C:y2= 2px(p>0), 坐标原点为O,M,N为C上两点,面积的最小值为4p2.

证明以O点为极点,以x轴正向为极轴方向建立极坐标系,则y2= 2px极坐标方程为:ρ2sin2θ= 2p·ρcosθ,即故而

将∆MFN面积推广成四边形面积时, 又可得以下结论:

结论3已知C:y2= 2px(p>0)的焦点为F,过焦点作抛物线的两条互相垂直的弦AB,MN,则四边形AMBN的面积最小值为8p2.

3 类比推广

如果将抛物线类比推广至椭圆及双曲线,第(2)问可类比成以下一般性的结论:

令sinθ-cosθ=t,则

证明以O点为极点,以x轴正向为极轴方向建立极坐标系,则椭圆C极坐标方程为:设故

结论6已知的左右焦点分别为F1,F2过右(或左)焦点作椭圆的两条互相垂直的弦AB,MN,则四边形AMBN的面积最小值为其中p表示焦点到对应准线的距离.

证明以F2点为极点, 以x轴正向为极轴方向建立极坐标系, 则椭圆C的极坐标方程为:

结论9已知双曲线的左右焦点分别为F1,F2, 过右(或左) 焦点作双曲线的两条互相垂直的弦AB,MN则四边形AMBN的面积最小值为其中p表示焦点到对应准线的距离.

结论7、8、9 证法类似于4、5、6,从略. 结论1,4,7,其实能变成统一结论:

结论10已知圆锥曲线C的焦点为F,M,N为圆锥曲线C上两点,则∆MFN面积的最小值为其中p表示焦点到对应准线的距离.

结论3、6、9 也可以成统一结论:

结论11已知圆锥曲线C的焦点为F,过F点作圆锥曲线的两条互相垂直的弦AB,MN. 则四边形AMBN的面积最小值为其中p表示焦点到对应准线的距离.

4 拓展延伸

结论12已知C:的左右焦点分别为F1,F2,过焦点F1,F2作椭圆的两条互相垂直的弦AB,MN,且AMBN是凸四边形(AB,MN的交点位于椭圆内部),则四边形AMBN面积最小值为其中p表示焦点到对应准线的距离.

证明由上知,以F1点为极点,以x轴正向为极轴方向建立极坐标系, 则椭圆C的极坐标方程为:因所以

从而