利用通用F-展开法求解ZK-BBM方程

陈 南

(厦门工学院,福建 厦门 361021)

0 引言

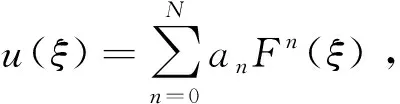
F′(ξ)=k+F2(ξ);

有椭圆方程:

F′2(ξ)=PF4(ξ)+QF2(ξ)+R.

在此基础上,把F-展开式F=F(ξ)所满足的方程推广到一般椭圆方程:

φ′2=c0+c1φ+c2φ2+c3φ3+c4φ4.

(1)

其中,ci(i=0,1,2,3,4)为参数.

通过研究一般椭圆方程(1)由系数之间的联系所求出的解,并借助这些解把F-展开法推广到一般椭圆方程的情形,称之为通用F-展开法[4].

本文对ZK-BBM方程进行研究,ZK-BBM方程的表达式如下:

ut+cux+a(u2)x+b(uxt+uyy)x=0.

(2)

目前,学者们对方程(2)进行了研究,分别运用F-展开法[5]、含负次幂项的F-展开法[5]、同伦摄动法[6]、G′/G展开法[7]、广义tanh函数法[8]、Sine-Cosine函数法[9]等方法,取得了不同类型的精确解.赵娟等[10]对ZK-BBM方程进行了扰动分析.本文选择扩展的椭圆方程方法(通用F-展开法)对ZK-BBM方程进行求解.

1 应用扩展的椭圆方程方法

对ZK-BBM方程作行波变换,u(x,y,t)=u(ξ),ξ=x+y+vt,则方程(2)变为

vu′+cu′+2auu′+b(v+1)u‴=0,

对上式积分得到

(v+c)u+au2+b(v+1)u″+k=0,

(3)

其中,k为积分常数.

假设方程(3)具有如下形式的解:

(4)

其中,n,ai(i=0,1,…,n)为待定常数,且φ(ξ)满足一般椭圆方程(1).

利用齐次平衡原则,可得n=2.故式(3)的解为

u(ξ)=a0+a1φ(ξ)+a2φ2(ξ),

(5)

其中,φ=φ(ξ)满足式(1),则有

(6)

利用式(1)(5)(6)可得

u′=a1φ′+2a2φφ′.

(7)

(8)

将式(5)(8)代入式(3),并令φi(i=0,1,2,3,4)的系数为零,得到关于a0,a1,a2,k,a,b,v,c的方程组:

(9)

φ3:2aa1a2+b(v+1)(2a1c4+5a2c3)=0,

(10)

(11)

φ:(v+c)a1+2aa0a1+b(v+1)(a1c2+3a2c1)=0,

(12)

(13)

解该方程组,得到

(14)

将式(14)代入(12)(13)可得c0,c1所满足的关系式.

2 ZK-BBM方程的精确解

(i)在式(1)中取c3=c0=c1=0,此时求解得到

(15)

(16)

(17)

将式(15)(16)(17)代入(5),得到方程(2)的具有扭状孤子解、三角函数和有理函数解:

(18)

(19)

(20)

将式(18)(19)代入(5),得到方程(2)的具有扭状孤子解、三角函数解:

(iii)在式(1)中取c3=c1=0,求解得到

(21)

(22)

(23)

在式(21)(22)(23)中,cn、sn、dn为Jacobi椭圆函数,m(0

将式(21)(22)(23)代入(5),得到方程(2)具有三种Jacobi椭圆函数解:

下面根据文献[4],运用Maple软件获得一般椭圆方程(1)在情况(iv)的四组新解.

(24)

(25)

(26)

(27)

将式(24)(25)(26)(27)代入(5),得到方程(2)的精确解:

3 结语

本文利用通用F-展开法对ZK-BBM方程进行求解,得到了ZK-BBM方程组的12组不同类型的解,包括孤子解、三角函数解、有理解和Jacobi椭圆函数解,进一步丰富了ZK-BBM方程的解系.后续工作可推广至其他方程.