面向多受灾区域与受限应急中心的双层耦合动态应急调度任务分配模型

段在鹏,俞思雅,黄月铃*,阳富强

(1.福州大学经济与管理学院,福建 福州 350108;2.福建省应急管理研究中心,福建 福州 350108;3.福州大学环境与安全工程学院,福建 福州 350108)

近年来,频发的事故灾害给现代社会系统提出了巨大的挑战[1],高效的应急救援是减少人员伤亡和财产损失的重要措施。Kemball-Cook等[2]于1984年首次提出应急物资调度的概念,之后应急物资调度优化问题已成为国内外学术界研究的热点问题。不同于一般的物资调度,灾后物资调度具有强时效性和弱经济性等特点[3],并且灾害初期,公众对物资调度的时效性和物资分配的合理性较为敏感,快速、高效地调配应急救援物资对应急资源调度尤为重要。基于此,多数的研究主要集中在应急物资调度模型的优化设计方面[4-5]。如:Yao等[6]为了优化传统车辆的调度,将路径不可靠性最小和车辆总体调度时间最少作为目标,构建了多目标应急车辆调度优化模型;Bodaghi等[7]以最小化调度完成时间和救援响应时间为目标,构建了双目标混合整数规划模型;Zhang等[8]通过引入分配公平性和需求紧迫度,构建了应急资源调度模型,旨在使物资短缺的损失最小化;王付宇等[9]考虑灾害初期资源稀缺性、运输路径破坏随机性、救援公平性等要素,建立了应急调度总成本最低及灾民满意度最大的多目标应急资源调度优化模型。除了以时间、成本最小或者需求满足率最大为研究目标外,也有学者认为在应急救援过程中应关注灾民的心理因素。如:王治莹等[10]考虑舆情传播中群众的风险感知能力,构建了以能力扩充为特色的0-1混合整数非线性模糊规划调度模型;宋英华等[11]通过设置最小化灾民痛苦心理效应目标,进而构建了应急资源分配-路径选择决策模型;王熹徽等[12]利用数值评定量表构造痛苦函数,估算了灾民的痛苦感知成本,并将该痛苦函数引入应急避难所选址-物资分配优化模型中。随着计算机技术的广泛应用,多种智能算法被开发出来,并成功应用于应急救援调度研究中。如:黄彩霞等[13]设计并改进了飞蛾扑火算法用于求解多目标应急资源调度模型;刘姝昱等[14]构建了多供应点-多需求点的应急食品供应优化调配模型,并借助Gurobi求解器编程对模型进行了求解;唐红亮等[15]为了实现多目标的并行协同优化,构建了多目标非线性离散混合整数规划地震应急物资调度模型,并利用自适应多目标粒子群优化算法对模型进行了启发式求解;Niu等[16]利用0-1的编码方式,设计出多目标遗传算法,用来求解受灾地区应急资源调度的最优方案;胡华等[17]针对地铁运营中断下公交桥接运输车辆应急调度问题中“运输需求远超单辆公交车辆运能”的特征,将动态系统仿真方法整合到带特定变异算子的改进遗传算法中用于求解模型;刘长石等[18]结合受灾群众非理性的攀比心理,构建了应急物资分配和运输双层模型,兼顾了公平和效率的应急物资调度和分配,并根据模型特点设计一种混合遗传算法求解模型。

灾害发生时,存在多个受灾区域、多个救援能力有限的出救点,但是学者们的研究往往较少考虑到救援能力受限和复杂应急救援调度的问题,而针对应急调度模型的目标多为最小化应急调度救援的时间,多将应急调度研究放置于静态应急救援情景中,认为应急物资的调度和分配是一次性完成的,没有考虑到受灾点的应急需求具有随机性、不确定性,且综合考虑动态和多层规划的模型较少,仍存在进一步研究的必要。此外,研究多从应急物资角度出发,没有考虑其他要素,但在实际救援中,应急救援并非单纯的物资派发,需求点往往涉及通讯维护、道路抢修、医疗救援等多类需求。基于此,本文将救援队伍作为特殊的应急救援资源,构建面向多受灾区域与受限应急中心的复杂双层耦合动态应急调度任务分配模型,并应用遗传算法对模型进行求解。

1多受灾区域与应急中心的双层耦合动态应急调度任务分配模型

1.1 模型的提出

应急救援效果会随着救援时间的延长而逐渐下降,“十四五国家应急体系规划”明确指出,救援中心应按照“就近调配”原则开展应急救援。在实际应急救援中,应急中心不仅要考虑时效性,更应该考虑调度的合理性,多数研究为避免资源浪费常以成本最小化进行应急资源分配,但由于灾情的随机性,灾点的应急需求情况会因为灾情的变化而不确定,而考虑经济性的应急救援任务分配方案往往会造成灾区救援力量不足[19]。因此,在灾害初期就要求应急中心不仅要满足灾点需求,更要调配具有较强救援能力的队伍前往灾区救援。

基于此,在应急救援过程中,救援距离、救援队伍数量以及救援队伍的救援能力均会影响应急救援效果。此外,为了合理分配应急救援任务,应急中心派遣的救援力量与受灾区域所需的救援力量应尽量满足供需平衡。因此,应急调度问题中任务分配方案优劣的评判标准主要有以下几点:

1) 应急中心距离受灾区域越近越好[20-21],应急中心距离受灾区域越近,受灾区域的人员得到救助的时间越早,受到二次伤害的风险越低。

2) 应急中心一次性派出的救援队伍应尽可能满足受灾区域的救援需求[22-23]。为了避免救援力量的分散,单位时间派出较多的救援队伍将有利于救援管理,并减少救援队伍在路上的损耗,提高应急救援效率。

3) 救援队伍的救援能力越强越好[24]。救援队伍的救援能力越强,救援队伍的救援效果越好,受灾区域得到的救援就越好。

4) 应急中心的救援任务负荷不能大于其救援力量储备[11-12]。若救援任务负荷大于应急中心救援力量储备,应急中心无法满足救援任务的需求,应急救援效果无法达到预期的目标。

由于灾害的突发性,应急中心的救援力量储备是有限度的,一旦派出的救援力量超过限度便无法提供持续救援,本文称为受限应急中心。本文构建多受灾区域与应急中心的双层耦合动态应急调度任务分配模型的优化目标是:在现有的应急中心中选出最优的应急中心,并在此基础上根据评判标准进行应急调度任务分配。

1.2 模型的构建

设共有n个应急中心,记应急中心集合为C={Ci|1≤i≤n},Ci为第i个应急中心,第i个应急中心其救援队伍储备为tCi,其中救援队伍储备tCi综合配备了救援人员、救援装备和交通车辆等应急资源[25]。应急中心C所辖救援队伍灾情处理能力为capture,capture具体表现为搜救能力、急救能力、护理能力、协助能力[26],应急中心基本救援能力为Ui,其中用capture与救援中心至灾点的距离distance来衡量应急中心的基本救援能力Ui,Ui随着各应急中心处理救援任务经验的变化而变化。

双层耦合动态应急调度任务分配模型的上层模型可描述为:根据应急中心的基本救援能力Ui,从n个应急中心中选出最适合救援m个受灾区域的s个参与应急救援的救援队伍;设受灾区域共有m个,将任务集合记为θ={θj|1≤j≤m},θj为第j个受灾区域,即第j项任务,第j个受灾区域θj所需的救援队伍总数为tθj,即第j项任务所需的救援队伍总数。

双层耦合动态应急调度任务分配模型的下层模型可抽象描述为:设有m个任务需要分配给s个应急中心完成。

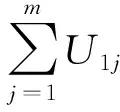
表1 应急中心的基本救援能力表

表2 应急中心的应急调度任务分配表

上层模型为

(1)

式中:f(a)为最优应急中心选择适应度函数;s为被选中参与应急救援的救援队伍数量;Ui为应急中心基本救援能力;ε为救援队伍供需惩罚系数;f(b)为应急调度任务分配适应度函数,如式(2)所示。

下层模型为

(2)

式中:uij为应急中心救援能力系数;α为应急中心储备量惩罚系数;β为应急中心队伍派遣量惩罚系数。

在上述双层耦合模型的基础上,针对不同阶段受灾区域的灾情变化程度,引入时间变量,建立双层耦合动态模型。在不同时刻下根据灾情的动态变化对应急调度最优任务分配方案进行调整,即在已经计算出的应急调度最优任务分配方案的基础上,对救援队伍进行调整。通过双层耦合动态模型计算出的结果为T=0时刻受灾区域的应急调度最优分配方案,但随着灾害发生后时间的变化,受灾区域所需的救援力量会发生变化。此时,救援队伍的救援能力增加经验系数ω,即:若受灾区域θj对救援力量的需求增加,优先从参与受灾区域救援的应急中心中调配救援队伍。根据受灾区域发生的变化,对应急救援方案做出调整。

以上双层耦合动态模型中,上层模型是选择适合进行应急救援工作的最佳应急中心,下层模型是在已选定的最佳应急中心的基础上对各应急中心的救援队伍进行任务派遣分配。上层模型是最终优化目标,下层模型的目的是应急调度任务分配,而上层模型的结果直接决定了下层模型的任务分配情况,同时下层模型在上层给出最佳应急救援方案的基础上做出最优的任务分配方案,再反馈给上层模型,从而对上层模型的目标进一步优化。最终的应急调度任务分配结果是上下层模型相互耦合计算的结果。

1.3 模型的展开

模型参数设置会影响最终结果,以下着重对模型中的关键参数进一步建模展开研究。

1)应急中心基本救援能力Ui。假定受灾区域有m个,表示有m项任务,记distanceij为第i个应急中心Ci与第j项任务(受灾区域θj)的距离,captureij为应急中心Ci所辖救援队伍执行第j项任务θj的处理能力,从低到高分为1～4个等级,一般地认为距离distanceij越小越好,处理能力captureij越大越好。Uij表示第i个应急中心执行第j项任务的基本救援能力;Ui表示第i个应急中心执行m个救援任务的基本救援能力,可表示为

(3)

2) 救援队伍供需惩罚系数ε。救援队伍供需惩罚系数可表示为

(4)

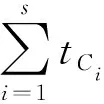
3) 应急中心救援能力系数u。记tij为第i个应急中心Ci对第j项任务(受灾区域θj)需派遣的救援队伍数量。除了距离distanceij和处理能力captureij外,应急中心一次性派遣的救援队伍数量也能表达救援能力的大小,避免资源的分散,节约运输成本。因此,第i个应急中心执行第j项任务的应急中心救援能力系数uij可表示为

(5)

4) 应急中心储备量惩罚系数α。应急中心储备量惩罚系数α可表示为

(6)

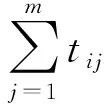
5) 应急中心救援队伍派遣量惩罚系数β。应急中心救援队伍派遣量惩罚系数β可表示为

(7)

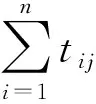
2 基于遗传算法的模型求解

上层遗传算法针对应急中心选择,在满足应急中心受限的情况下,考虑应急中心储备量限制及其他约束条件并附带下层遗传算法的求解目标,选出最佳的应急中心,进而得到下层模型各救援队伍的应急调度最优任务安排。遗传算法[5]的求解步骤主要包括编码、定义适应度函数、确定遗传策略 (群体大小、选择、交叉、变异等)。本文着重对编码、策略适应度函数、交叉策略、变异策略4个关键步骤进行阐述。

2.1 编码方案与个体表示

1) 上层模型0或1编码。上层模型的目标是选出最优的应急中心,因此上层遗传算法采用0-1编码的方式。如图1所示,随机产生一个长度为n的0或1组成的基因序列,1表示该应急中心被选中,0表示该应急中心未被选中。上层模型0或1编码的基因序列示例如图2所示。

图1 长度为n的0或1组成的基因序列Fig.1 Gene sequence consisting of 0 or 1 of length n

图2 上层模型0或1编码的基因序列示例Fig.2 Examples of gene sequences encoded by upper model 0 or 1

如图2所示的基因序列,表示应急中心C2、C3未被选中参与应急救援任务,应急中心C1、C2被选中参与应急救援任务。

2) 下层模型整数编码。下层模型的目标是在选出的应急中心基础上进行应急调度任务分配,因救援队伍数量为整数,故下层遗传算法采用整数编码的方式。如图3所示,随机产生一个长度为m×n的整数序列。

图3 长度为m×n的整数基因序列Fig.3 Integer gene sequences of length m×n

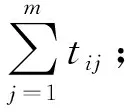
(8)

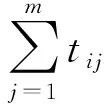
例如如图4所示的基因序列,表示有3个受灾区域θ1、θ2、θ3,以及根据图2选出的2个应急中心C1、C4,未被选中的应急中心对受灾区域派遣的救援队伍数量均为0。应急中心C1派遣5支救援队伍,C4派遣1支救援队伍参与救援第一项任务(受灾区域θ1);应急中心C1派遣5支救援队伍,应急中心C4派遣2支救援队伍参与救援第二项任务(受灾区域θ2);同理,可理解任务θ3。

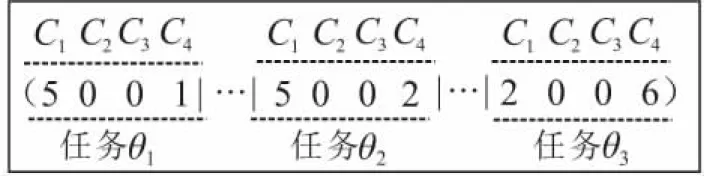
图4 下层模型整数编码基因序列示例Fig.4 Example of integer coding gene sequence of the lower model

2.2 适应度函数定义

由于适应度函数与群体中的个体优劣相联系,故本文将双层耦合动态应急调度任务分配模型如式(1)、(2)所示,分别选取上层模型和下层模型的适应度函数。下层遗传算法将目标函数值(即应急中心对应的救援队伍分配方案)反馈到上层,上层遗传算法输出目标函数值在上下层遗传算法的不断反馈中达到优化,最后基于上下层模型的适应度函数结果,采用轮盘赌策略选择个体。

上层模型的适应度函数为

(9)

下层模型的适应度函数为

(10)

该双层动态应急调度任务分配模型的算法框架,如图5所示。

图5 双层动态应急调度任务分配模型的算法框架图Fig.5 Algorithm framework diagram of two-layer dynamic emergency scheduling task allocation model

2.3 交叉策略确定

双亲交叉能避免局部收敛,单亲交叉能加快收敛效率,因此双层耦合动态应急调度任务分配模型结合两种交叉方式:在上层模型中,本文选用双亲交叉的单点交叉策略;在下层模型中,本文设计新的单亲交叉策略。

1) 上层模型的双亲单点交叉策略。在遗传算法中产生新个体的基本操作是染色体的交叉(也称基因重组)。双亲单点交叉策略能避免产生的结果只是局部最优解。上层模型的双亲交叉策略示例,如图6所示。

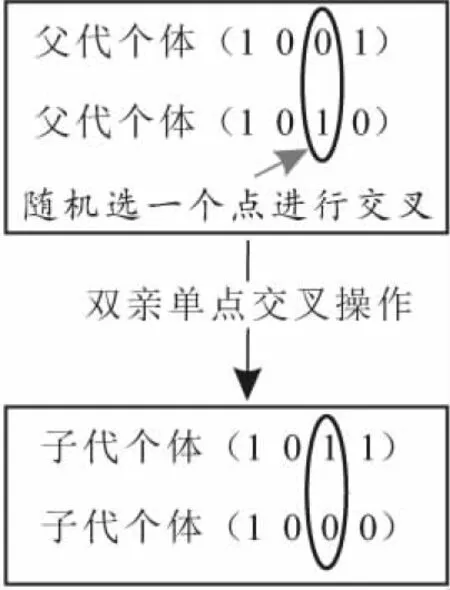
图6 上层模型的双亲单点交叉示例Fig.6 Parental single point crossover example of the upper layer model

如图6所示的双亲单点交叉操作表示:两个父代个体中选中参与救援的应急中心C3与另一个父代中未被选中的参与救援的应急中心C3交叉互换,得到两个新的个体。

2) 下层模型的单亲交叉策略。由于在单亲交叉中,母体基因段上的任意若干对基因交换的位置是随机的,所以为了避免无效个体的大量产生,本文规定只有“同一救援任务下的不同应急中心”的情况可以进行互相交叉。下层模型的单亲交叉策略示例,如图7所示。

图7 下层模型的单亲交叉示例Fig.7 Example of single parent mutation of the lower layer model

如图7所示的单亲交叉操作表示:应急中心C4参与任务θ1的1支救援队伍与参与任务θ3的6支救援队伍交叉互换,得到一个新的个体。

2.4 变异策略确定

单亲变异操作就是随机地对母体上的若干基因位进行逆转而产生新的个体。

1) 上层模型的0或1变异策略。在上层模型中,本文规定0或1编码的染色体变异方式为基因位随机由0变为1或者由1变为0,如图8所示。

图8 上层模型单亲突变示例Fig.8 Example of single parent mutation of the upper layer model

如图8所示的单亲突变操作表示:随机地,第一个基因位由1变为0,第三个基因位由0变为1,即选中参与救援的应急中心C1,C4变为应急中心,C1参与C4救援。

2) 上层模型的整数变异策略。在下层模型中,本文规定只有被选中参与救援的应急中心的救援队伍数量可在基因位随机加减一个整数,如图9所示。

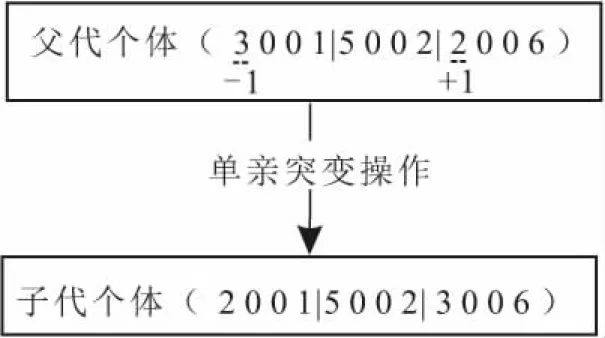
图9 下层模型单亲突变示例Fig.9 Example of single parent mutation of the lower layer model

如图9所示的单亲突变操作表示:随机地,应急中心C1参与救援任务θ1的救援队伍减少1支,应急中心C4参与救援任务θ2的救援队伍增加1支。

3 实例分析

3.1 问题描述

某次地震灾害应急中,受灾区域和应急中心的拓扑关系见图10。其中,圆面积的大小表示受灾区域对救援队伍的需求量;连接线上的数值表示各应急中心到受灾区域的距离;连接线的粗细程度表示应急中心对该受灾区域救援能力的等级大小,本文分为4级,连接线由粗到细依次为4～1级。

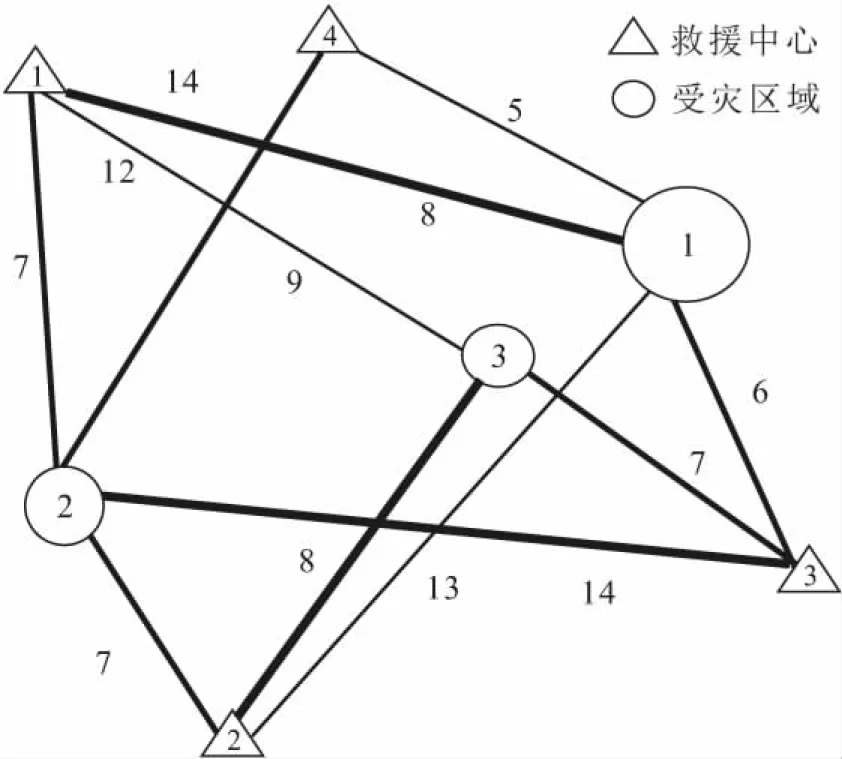
图10 应急中心与受灾区域拓扑关系图Fig.10 Topological relationship between the rescue center and the disaster area

由图10可知:受灾区域共有3个,记为θ={θj|1≤j≤3},θj为第j个受灾区域,该3个受灾区域所需的救援队伍数量依次为7、5、6支。应急中心共有4个,记为C={Ci|1≤i≤4},Ci为第i个应急中心,其救援队伍储备均为10支。例如表3中,4/14表示应急中心C1到受灾区域θ1的距离为14 km,应急中心C1所辖救援队伍执行任务θ1的处理能力为4级,详细数据见表3。灾害发生后,不同时刻受灾区域的救援队伍需求见表4。

表3 应急中心详细数据表

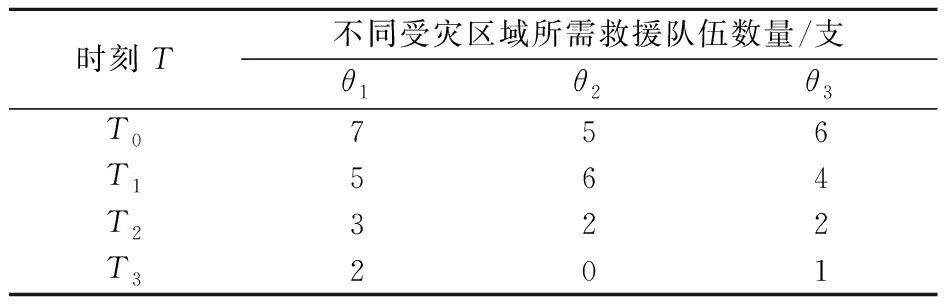
表4 不同时刻受灾区域的救援队伍需求

3.2 模型求解

遗传算法试验参数设置如下:上层模型种群大小为100,最大进化迭代数为100,遗传代沟为0.9,双亲交叉概率为0.9,变异概率为0.1;下层模型种群大小为100,最大进化迭代数为150,单亲交叉概率为0.9,变异概率为0.1。

具体求解过程见2.2节。求解出的上层迭代图见图11。

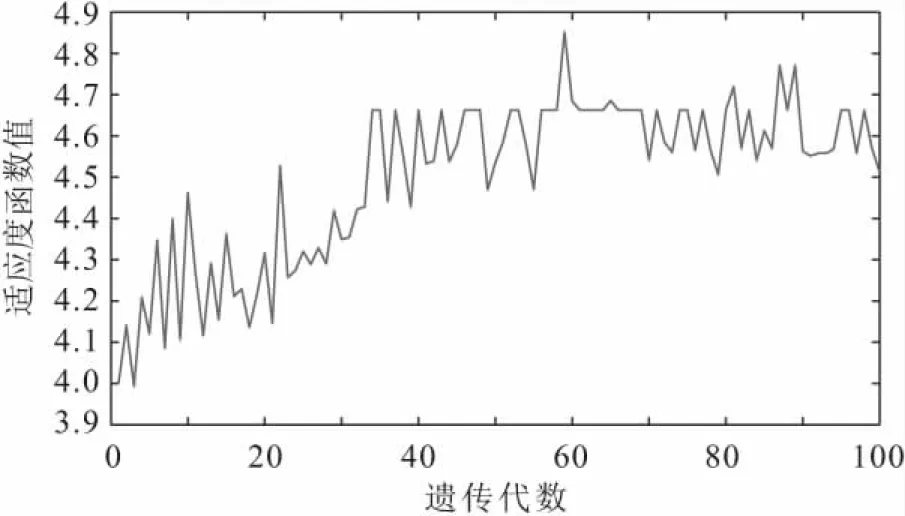
图11 上层模型迭代图Fig.11 Iterative diagram of the upper layer model

在图11中,上层模型适应度最大的5个值对应的应急中心选择方案有3种,为①[0,0,1,1]、②[1,1,0,1]、③[0,1,0,1],分别对应下层救援队伍数量分配迭代图,如图12、图13、图14所示。

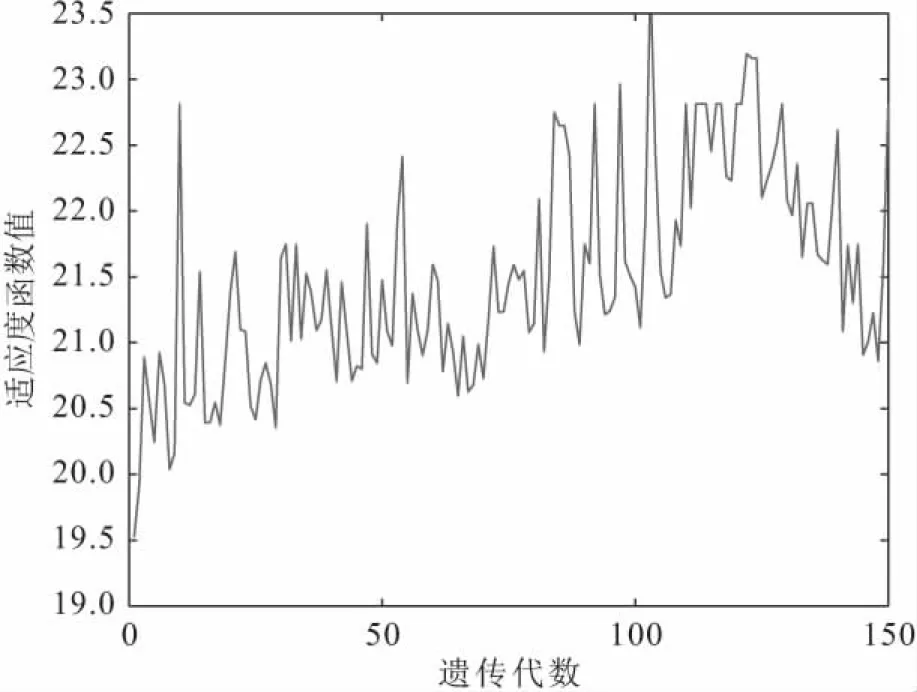
图12 下层模型迭代图①Fig.12 Iterative diagram of the lower layer model①

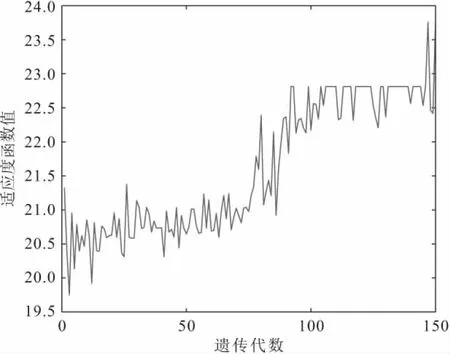
图13 下层模型迭代图②Fig.13 Iterative diagram of the lower layer model②

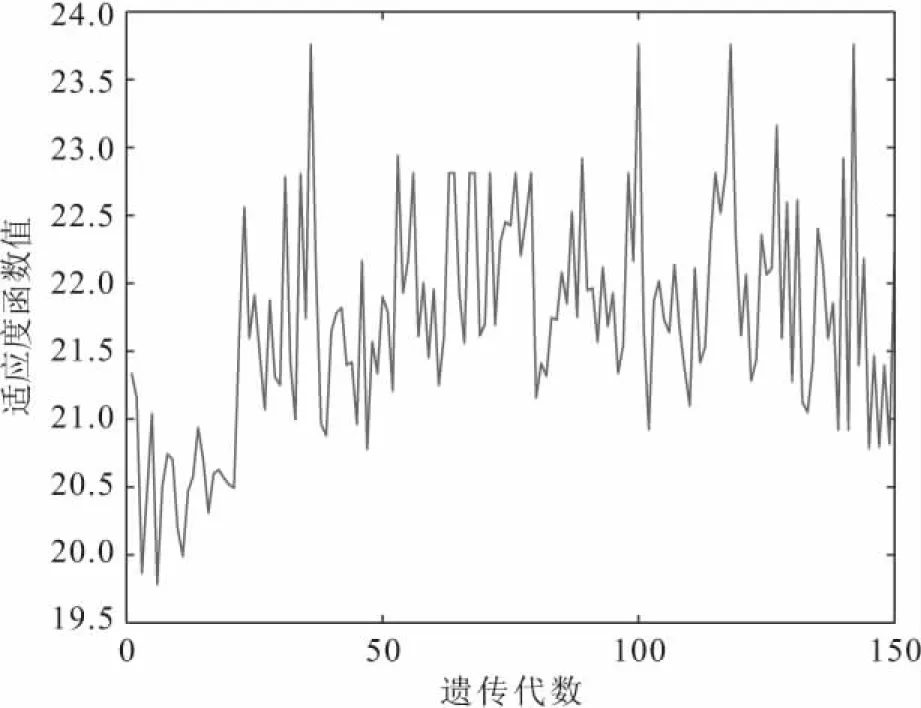
图14 下层模型迭代图③Fig.14 Iterative diagram of the lower layer model③

由图12、图13、图14可以看出,应急中心3种选择方案对应的下层最大适应度值都在23左右,并且应急中心选择方案②对应的下层模型迭代图的收敛效果更稳定,因此应急中心选择的最优方案为方案②[1,1,0,1],对应的救援队伍任务分配方案为(0 0 0 7|5 0 0 0|0 6 0 0)。以应急中心C2为例,解读应急中心派遣的救援队伍最优分配方案为应急中心C2对θ1、θ2、θ3受灾区域分别派出0、0、6支救援队伍,具体见表5。

表5 不同应急中心派遣的救援队伍最优分配方案表

3.3 动态情景调度

当灾害发生一段时间后,此时在T1时刻,根据表4可知受灾区域θ1、θ2、θ3所需的救援队伍数量分别变为5、6、4支救援队伍。在已经计算出的最优任务分配方案的基础上,对救援队伍进行调整,调整原则遵循:①尽可能从参与救援的应急中心调配救援队伍;②救援力量过剩时,从救援能力弱的应急中心减少参与救援的救援队伍数量;③参与救援的救援队伍尽可能为同一个应急中心。最终利用Matlab软件计算得出的不同时刻应急中心派遣的救援队伍最优任务分配方案见表6。以应急中心C1为例,解读不同时刻应急中心派遣的救援队伍任务分配方案为:T1时刻,应急中心C1对θ1、θ2、θ3受灾区域分别派出4、0、0支救援队伍。

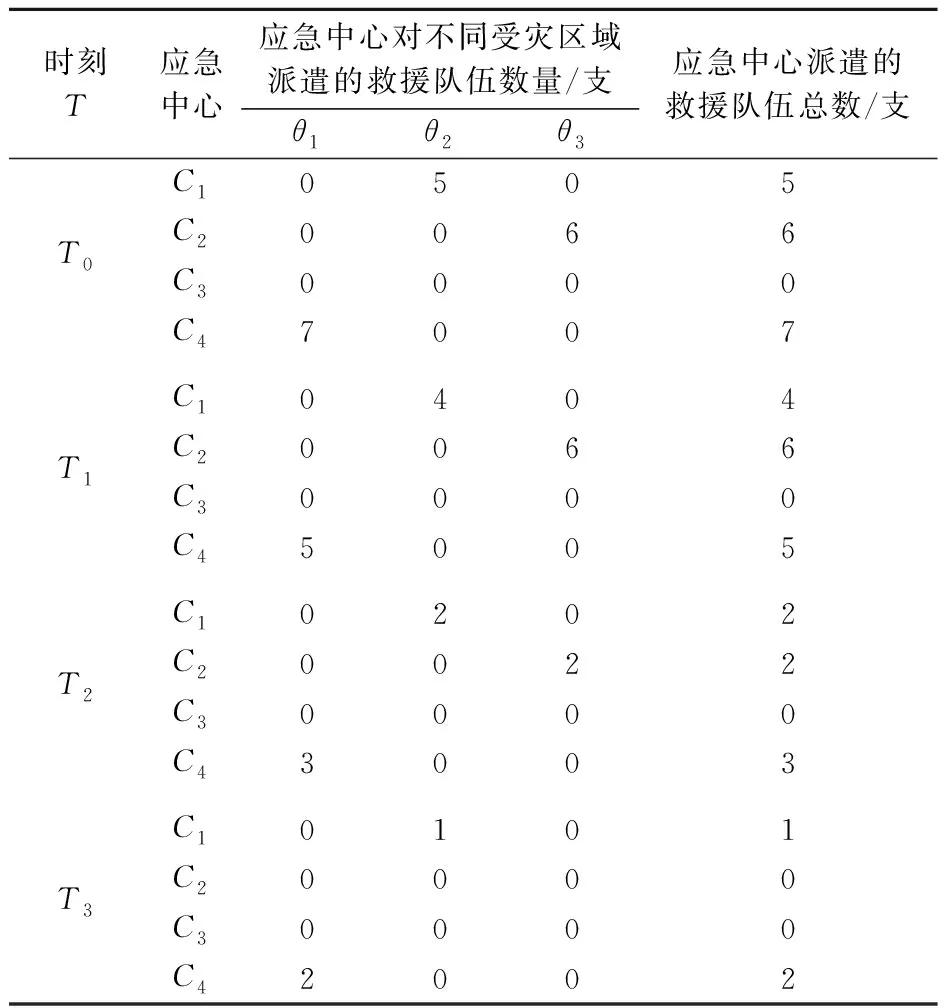
表6 不同时刻应急中心派遣的救援队伍最优任务分配方案表

4 结 论

1) 根据救援距离、救援队伍的救援能力、应急中心受限情况以及受灾区域的救援需求,定义5个约束函数,设计出上层应急中心选择和下层救援队伍数量分配的双层耦合模型,并在得到最合适的应急中心的基础上,对救援队伍数量进行最优应急调度任务分配,再反馈给上层,实现对上层模型的进一步优化。因此,双层耦合模型在进行应急调度方案选择时考虑的因素更全面,得出的方案更合理。

2) 随着时间的发展,需要对应急调度分配的救援力量和物资进行再调整,避免救援资源的浪费。因此,在双层耦合模型的基础上引入时间变量,构造双层耦合动态模型,根据受灾区域对救援力量的需求发生变化,遵循优先从参与受灾区域救援的应急中心中调配救援队伍的原则,对应急调度任务分配方案做出了相应的调整,使得救援调度更加灵活和贴合实际。

3) 根据上层模型和下层模型的特点以及上、下层模型之间的耦合关系,设计0或1编码和整数编码方式,并设计单亲交叉方式,将单亲和双亲交叉综合运用,兼顾高效性和稳定性,同时还设计了0或1变异和整数变异策略,通过仿真计算,结果表明该双层耦合动态模型结果合理,符合实际。

4) 从仿真结果来看,在上层模型中,由于上层模型的适应度函数受下层模型适应度函数的影响,最大适应度值对应的应急中心应急调度任务分配方案不唯一,因此还需要利用下层模型做进一步分析,从而确定上层应急中心的应急调度任务分配。相比于单层模型,双层耦合模型计算速度较慢,但考虑的因素更多,得出的应急救援方案也较合理。另外,考虑时间影响的双层耦合动态模型比双层耦合模型更灵活、更贴合实际情况,从而使得救援资源利用率达到更大化。