模型参数点估计的可靠性：以CDM为例*

刘彦楼 陈启山 王一鸣 姜晓彤

模型参数点估计的可靠性：以CDM为例*

刘彦楼1,2陈启山3,4王一鸣2姜晓彤2

(1曲阜师范大学教育大数据研究院;2曲阜师范大学心理学院, 山东 济宁 273165) (3“儿童青少年阅读与发展”教育部哲学社会科学实验室(华南师范大学);4华南师范大学心理学院, 广州 510631)

心理学研究中, 不恰当的模型参数估计框架或收敛准则严重影响模型参数点估计的可靠性, 进而影响到研究结论的可靠性。本研究提出了基于MLE-EM的CDM模型参数估计新框架, 以及新收敛判断方法。通过模拟研究与实证数据分析的方式, 探索了新参数估计框架和新收敛判断方法的表现, 并与已有模型参数估计框架及收敛判断方法进行了比较。结果显示, 新的模型参数估计框架及收敛准则的表现优于已有的模型参数估计框架及收敛准则, 能有效提高模型参数点估计的可靠性。

参数估计, 点估计, 收敛准则, 认知诊断模型

1 引言

自然科学及社会科学各个领域中, 研究结论的可靠性(研究结论可以被信赖的程度), 尤其是研究结果的可重复性(replication)受到极大关注(参见：胡传鹏等, 2016; Begley & Ellis, 2012; Ioannidis, 2005, 2008; Tajika et al., 2015)。Nature杂志对此进行了一项调查, 发现70%以上的研究者无法重复他人实验, 50%以上的研究者无法重复他们自己的实验(Baker, 2016)。心理学领域中, 研究者对可重复性问题出现的比例、可能的原因展开了探讨, 并从统计方法和研究实践两方面提出了解决方案(例如, 可参考《心理学报》的投稿指南及论文自检报告或American Psychological Association, 2020等)。

模型参数点估计的可靠性是研究结论可靠性的基础。因此, 如何提高模型参数估计值的可靠性, 进而提高研究结果的可重复性是本文将要探讨的主要问题。

认知诊断(或者是诊断分类)使用心理计量模型推断被试可观察的外显行为与其潜在的多维、细粒度的心理特质(如心理结构、技能、加工过程或策略等, 统称为属性)之间的关系(Rupp et al., 2010)。认知诊断模型(cognitive diagnostic model, CDM)在心理、教育、社会、生物以及其他多个领域中得到了越来越多的关注(Sorrel et al., 2016; Wu et al., 2017)。因此, 本文以CDM为例, 探讨模型参数点估计的可靠性问题。

目前, 极大似然期望最大化算法(maximum likelihood estimation using the expectation maximization algorithm, MLE-EM)是应用最广泛的CDM模型参数估计方法之一(de la Torre, 2009, 2011; von Davier, 2008)。例如, 在R语言中的(George et al., 2016)、(Ma & de la Torre, 2020)软件包以及,,、(Sen & Terz, 2020; Templin & Hoffman, 2013)等软件中均可使用MLE-EM估计CDM的模型参数。理想条件下, 使用MLE-EM方法能够获得具有渐近性、一致性等优良特性的点估计值。但是, 研究者指出使用MLE-EM算法估计CDM模型参数时, 可能会遇到的问题有：模型参数不收敛、项目参数极端值、(较差的)局部最优解以及边界值等(DeCarlo, 2011, 2019; Ma & Guo, 2019; Ma & Jiang, 2021; Philipp et al., 2018; Templin & Bradshaw, 2014; Zeng et al., 2023)。MLE-EM估计的一般过程是, 给定模型参数初始值, 迭代进行E步(期望步)和M步(最大化步), 满足特定的收敛准则(convergence criterion或termination criterion)后停止迭代, 输出模型参数的点估计值。因此, 可以从参数估计框架(包括模型参数初始值设置、EM过程等)及收敛准则等方面着手解决模型参数点估计可靠性问题。

本文将在第2部分阐述CDM模型参数估计中模型参数估计框架及收敛准则存在的问题, 以及这两个问题对于参数估计可靠性的影响; 在第3部分详细说明新提出的模型参数估计框架及收敛准则, 并在第4部分通过模拟研究比较新方法与已有方法在模型参数估计可靠性方面的表现; 第5部分是实证数据分析, 目的是检验新提出的模型参数估计框架及收敛准则在估计CDM模型参数时的表现, 并与软件包的表现进行比较; 最后是讨论与展望。

2 CDM及其模型参数估计中存在的问题

在这一部分, 将首先介绍饱和CDM及属性层级CDM(hierarchical cognitive diagnostic model, HCDM); 然后以此为基础阐述模型参数估计中存在的不收敛、项目参数极端值、(较差的)局部最优解以及边界值等问题。

2.1 饱和CDM及HCDM

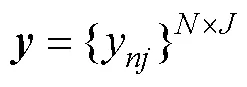
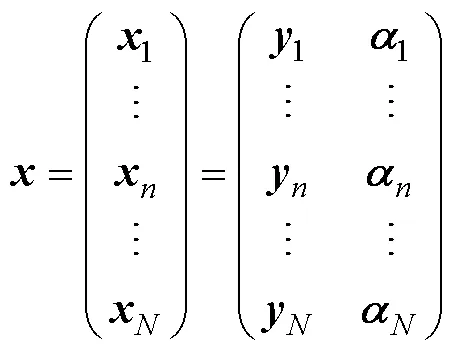
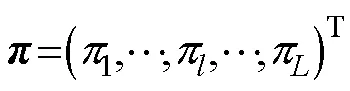
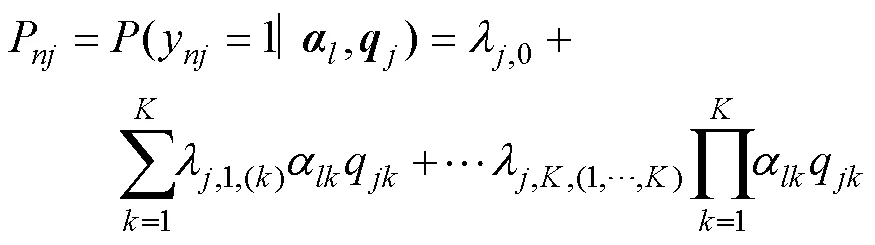
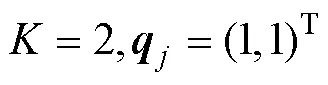
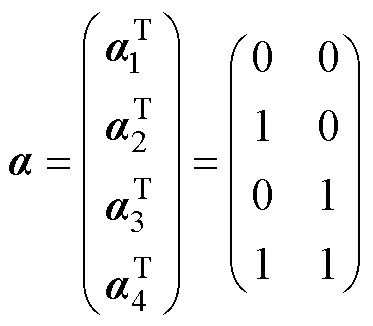
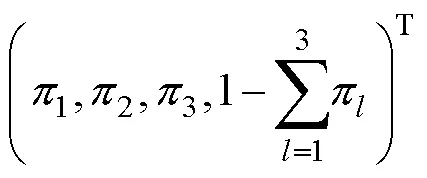
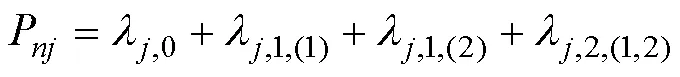
根据属性层级关系, HCDM中所有允许存在的属性掌握模式是,

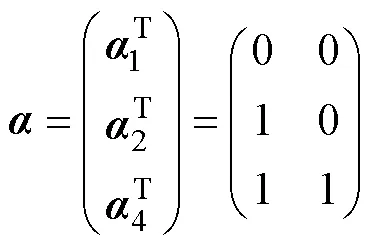
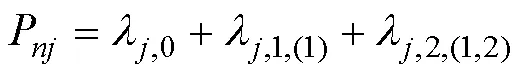
比较表达式(3)和(5), 及表达式(4)和(6), 可以发现将饱和CDM中的一些结构参数以及项目参数约束为0, 可获得HCDM。也就是, 如果“真”模型为HCDM, 但使用饱和CDM估计模型参数时, 部分模型参数的真值等于0。一些结构模型参数真值等于0, 意味着这些参数在参数空间的下界, 如果不解决这种这类边界值问题可能会造成MLE-EM参数估计存在多种问题。

2.2 CDM模型参数估计中可能存在的问题

使用CDM拟合作答反应数据时, 如果模型参数过多、样本量较小, 或者是模型参数中存在边界值尤其是结构参数中存在边界值等问题时, 可能导致模型参数不收敛、项目参数存在极端值或者是存在多个局部最优解等问题(Ma & Jiang, 2021; Templin & Bradshaw, 2014)。

CDM的项目正确作答概率及结构参数均介于[0,1]之间。在估计模型参数时可能会遇到项目参数或结构参数在参数空间的上界或下界的问题, 这可能会造成模型参数无法估计, 或者是造成模型参数的标准误过大甚至是无法求解。Ma和Jiang (2021)提出贝叶斯众数估计及单调约束, 估计G-DINA模型的项目参数。但是, 他们的研究指出贝叶斯众数估计或贝叶斯众数与单调约束结合的算法估计获得的项目参数可能是有偏的; 另外, 他们也指出在实践应用中先验分布的选择需要非常谨慎, 因为不恰当的先验信息可能会导致误导性的、甚至是错误的结果。为将模型参数估计值约束在适当的边界中, Yamaguchi (2023)进一步提出将结构参数也要加以约束。然而, 当属性之间存在层级关系, 但是使用饱和结构模型估计参数时, 有些结构参数的真值等于0, 以不恰当的先验约束使其远离0的做法是不对的。

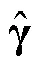
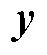
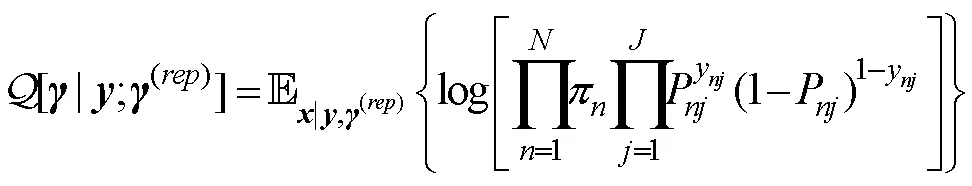
以饱和G-DINA模型的参数估计为例, 在M步中, 经过公式推导(参考, de la Torre, 2009, 2011)可以求得更新后的第种属性掌握模式下项目正确作答概率的表达式,

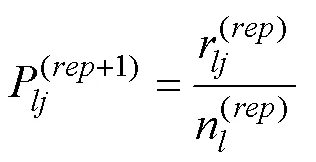
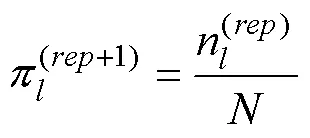
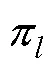
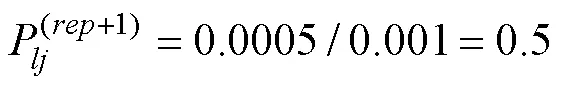
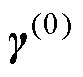
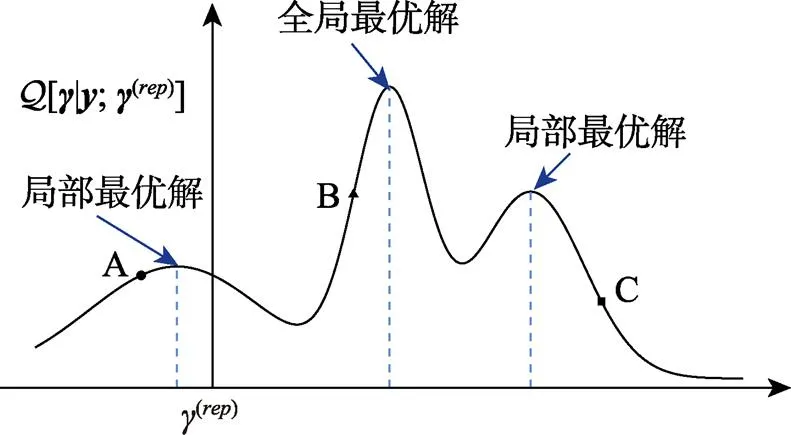
图1 单个参数的局部最优解或全局最优解的简单示例

2.3 CDM模型参数估计的收敛准则

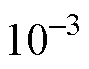
当前, 可以用于判断CDM模型参数估计是否收敛的方法至少有6种(George et al., 2016; Ma & de la Torre, 2020; Ma et al., 2022; Robitzsch et al., 2022; Rupp & van Rijn, 2018)。

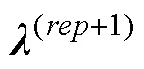
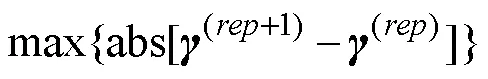
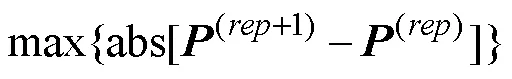
第四种是项目正确作答概率和结构参数组成的向量的差的绝对值。这种方法以第三种方法为基础, 将结构参数也纳入考虑, 因此不再赘述。可以发现, 以上4种收敛判断方法是基于全部或部分模型参数的。CDM中项目正确作答概率一般是由项目参数组合而成, 也就是说相对于项目参数而言, 项目正确作答概率差这种方法更容易满足模型收敛准则。

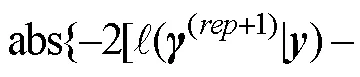
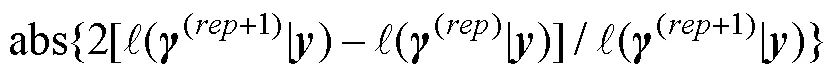
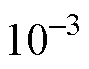
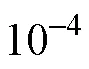
可以发现, 研究者使用的收敛准则有很大差别。因此, 相同计量模型条件下, 不同的收敛准则是否会对模型参数点估计的可靠性产生影响; 如果产生影响, 在目前所有可用的模型参数估计收敛判断方法中, 哪种效果是最好的; 或者是能否开发一种具有广泛适用性的方法提高CDM模型参数点估计的可靠性是一个需要解决的重要问题。

3 新的模型参数估计框架及收敛准则

如前所述CDM模型参数估计中的边界值、局部最优解、项目参数极端值、模型参数不收敛, 以及收敛准则设置等可能会对模型参数点估计的可靠性产生影响, 进而可能会影响到研究结果的可重复性。因此, 本文提出新的模型参数估计框架试图解决2.2部分提及的模型参数估计中可能存在的问题; 提出新的收敛准则试图解决2.3部分提及的收敛准则可能存在的问题。

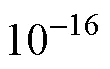
其次, 阐述局部最优解、项目参数极端值、模型参数不收敛等问题的综合解决方法。

模型参数收敛判断中, 设置最大迭代次数的唯一目的是避免模型参数估计程序陷入到无限(或近乎于无限)循环。然而, 在模型参数本应收敛的情况下, 如果将最大收敛次数设置的过小, 可能会使得MLE-EM过早结束循环, 造成不收敛的错误结果。解决不收敛问题的首要一步是设置足够大的收敛次数, 因此本研究中将最大收敛次数设置为50000。

CDM的模型参数仅存在全局最优解的一个前提是公式(7)为凸函数。但是, 这个前提有时未必成立, 导致模型参数可靠性变差。因此, 参考Ma和Guo (2019)的相关研究, 本文提出使用多个初始值计算CDM模型参数。即, 遇到不收敛或项目参数存在极端值时重新生成初始值并计算, 如果新初始值条件下的模型参数收敛、对数似然函数值大于先前的值、且项目参数不存在极端值时, 使用新的估计值作为最终的模型参数估计值。在接下来的部分将这个新的模型参数估计框架称为, 并以此为基础探讨各种收敛准则的表现。由于在特定条件下, 需要对于同一观察数据矩阵, 在多个不同初始值下进行模型参数估计, 运算量可能会比较大。因此参考以往研究(刘彦楼, 2022),程序计算量大的部分采用C++语言及并行计算进行。特别说明的是,程序已上传到科学数据银行, 感兴趣的读者可以自行下载使用。

最后, 阐述本文中新提出的收敛判断方法。

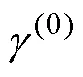
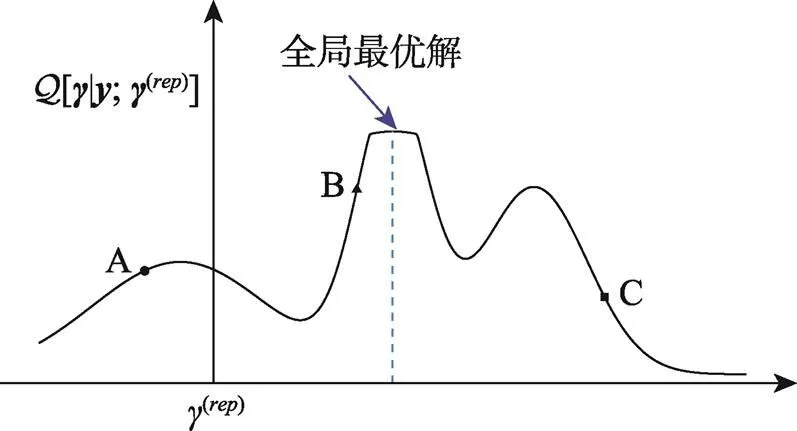
图2 对数似然函数差收敛判断方法可能缺陷的简单示例

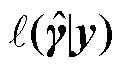
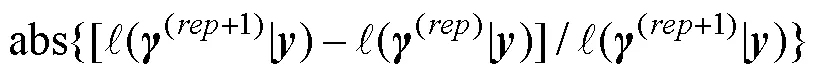
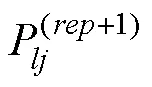
4 模拟研究

4.1 研究目的

本研究重点关注的问题是：新提出的模型参数估计框架及收敛准则能否有效提高模型参数点估计值的可靠性。即, 新提出的框架下的综合判断方法是否优于现有框架下的方法, 能否在尽量保证参数在合理范围内的前提下, 获得使得似然函数最大的参数估计值。具体包括：(1)数据生成模型与拟合模型均为饱和G-DINA时, 即模型完全正确设定条件下各种收敛准则的表现; (2)数据生成模型为HCDM但使用饱和G-DINA拟合时, 即模型中存在边界值时各收敛准则的表现。

4.2 研究方法

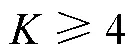
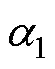
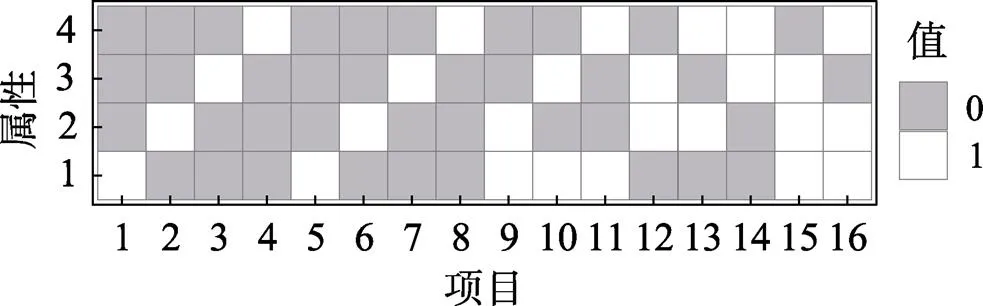
图3 模拟研究中J = 16的Q矩阵

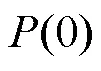
4.3 评价指标

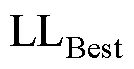
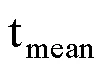
4.4 模拟结果

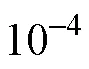
4.4.1 饱和CDM生成数据时各收敛准则的表现

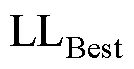
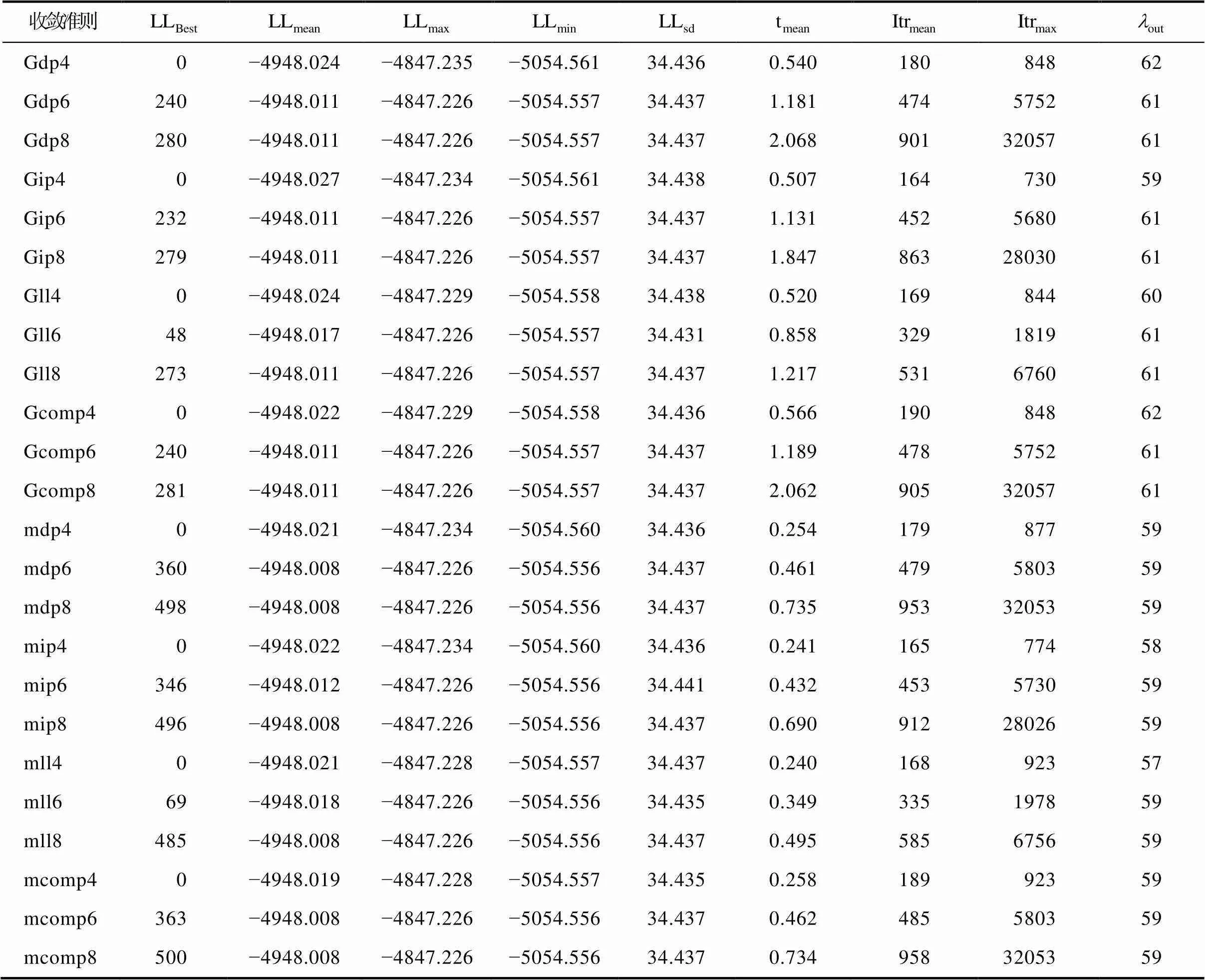
表1 饱和CDM生成数据, J = 16, N = 500条件下的模拟结果

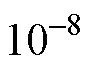
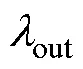
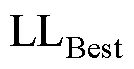
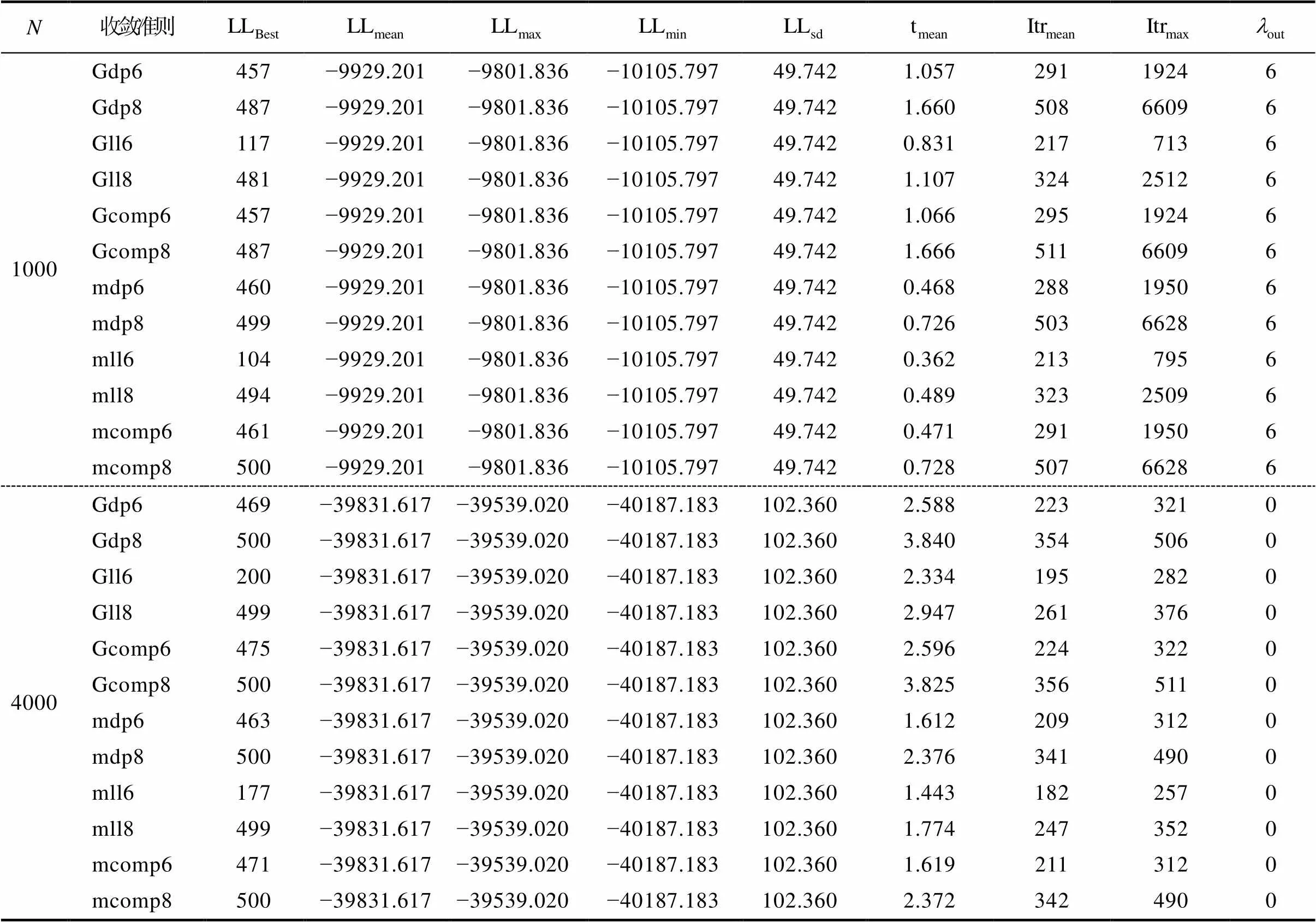
表2 饱和CDM生成数据, J = 16, N = 1000及4000条件下的模拟结果

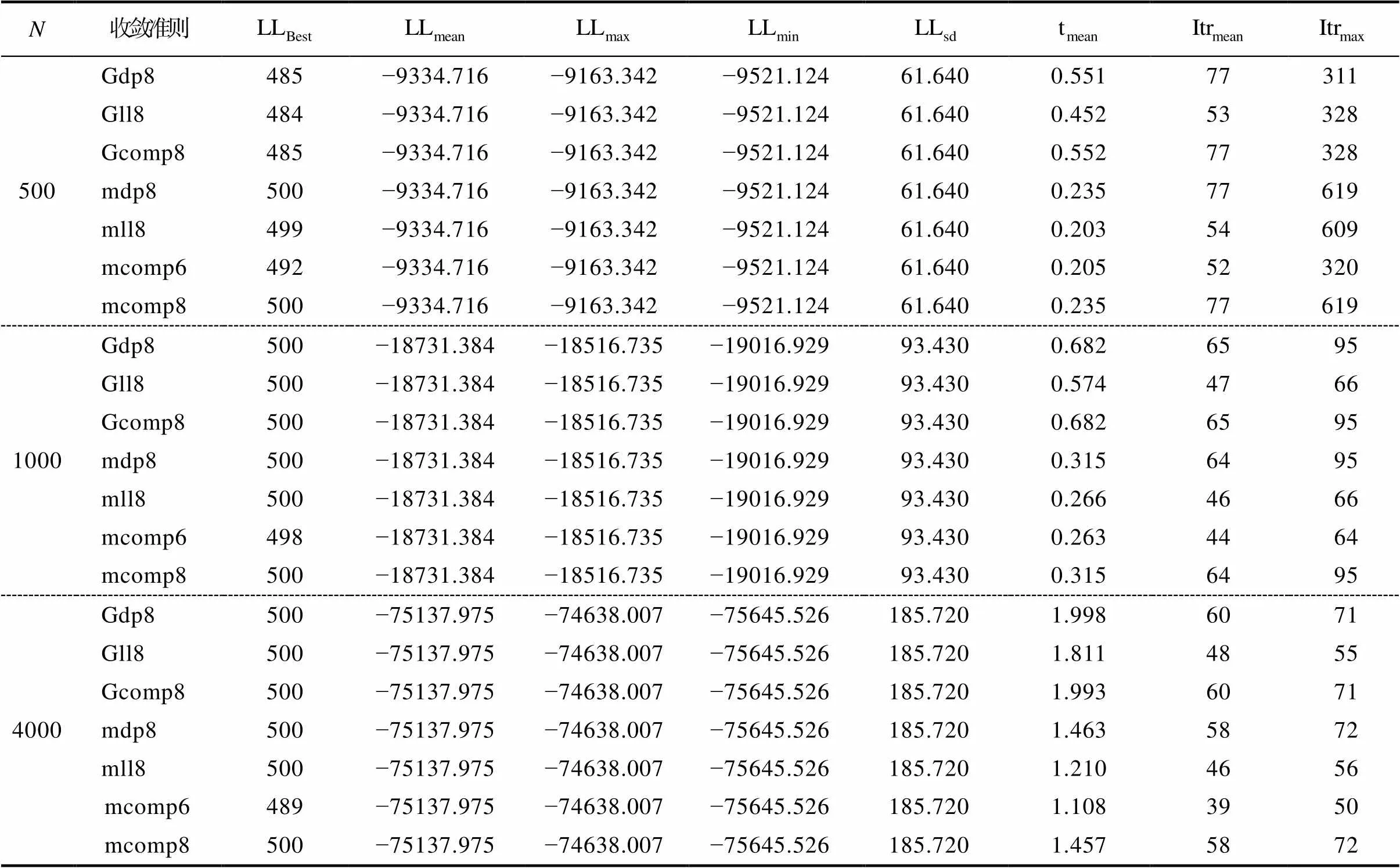
表3 饱和CDM生成数据, J = 32条件下的模拟结果

4.4.2 HCDM生成数据时各收敛准则的表现

表4到表6呈现的是通过HCDM (前3个属性是线性层级关系)生成作答反应数据但使用饱和CDM估计模型参数条件下的模拟结果。

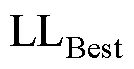
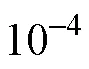
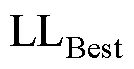
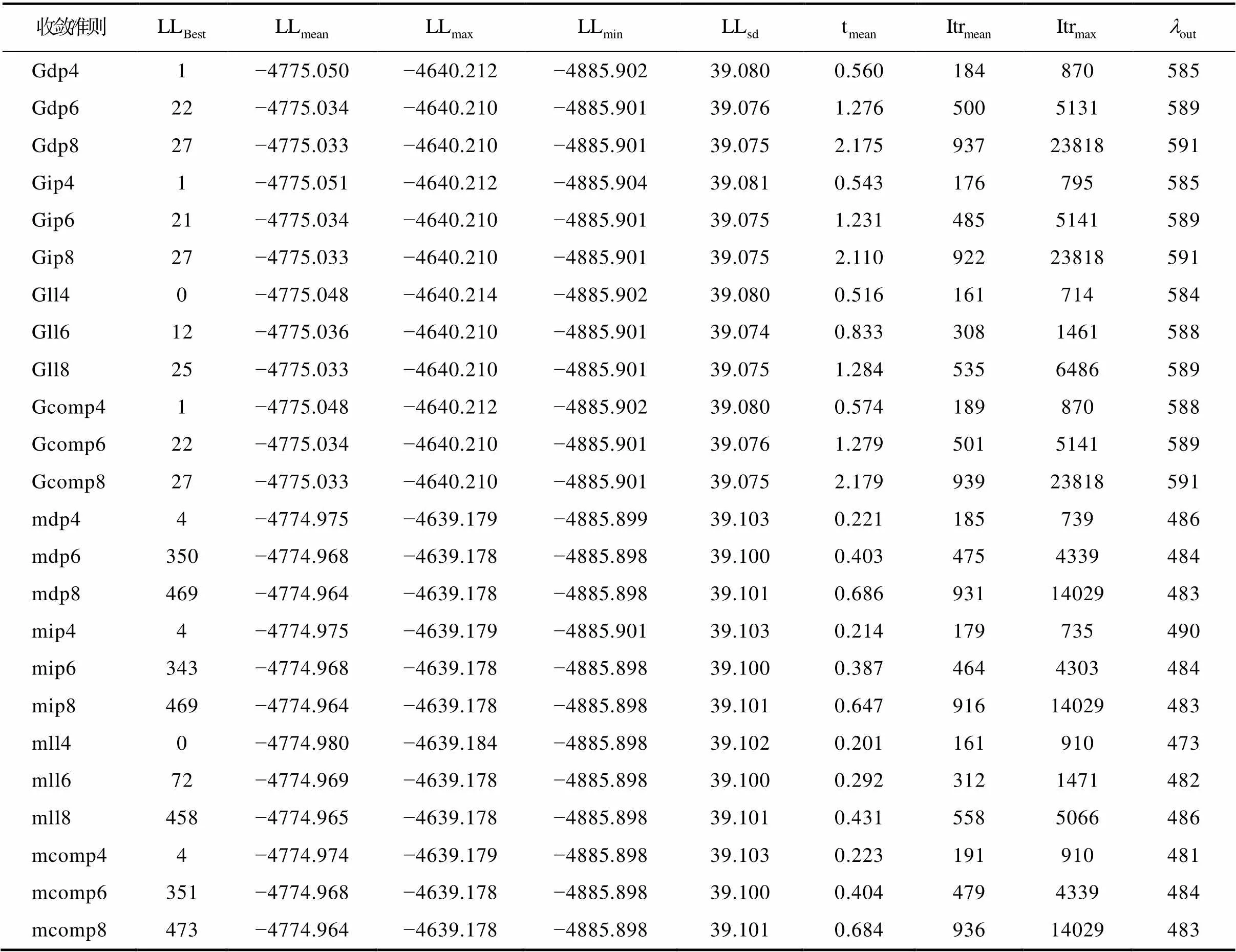
表4 HCDM生成数据, J = 16, N = 500条件下的模拟结果

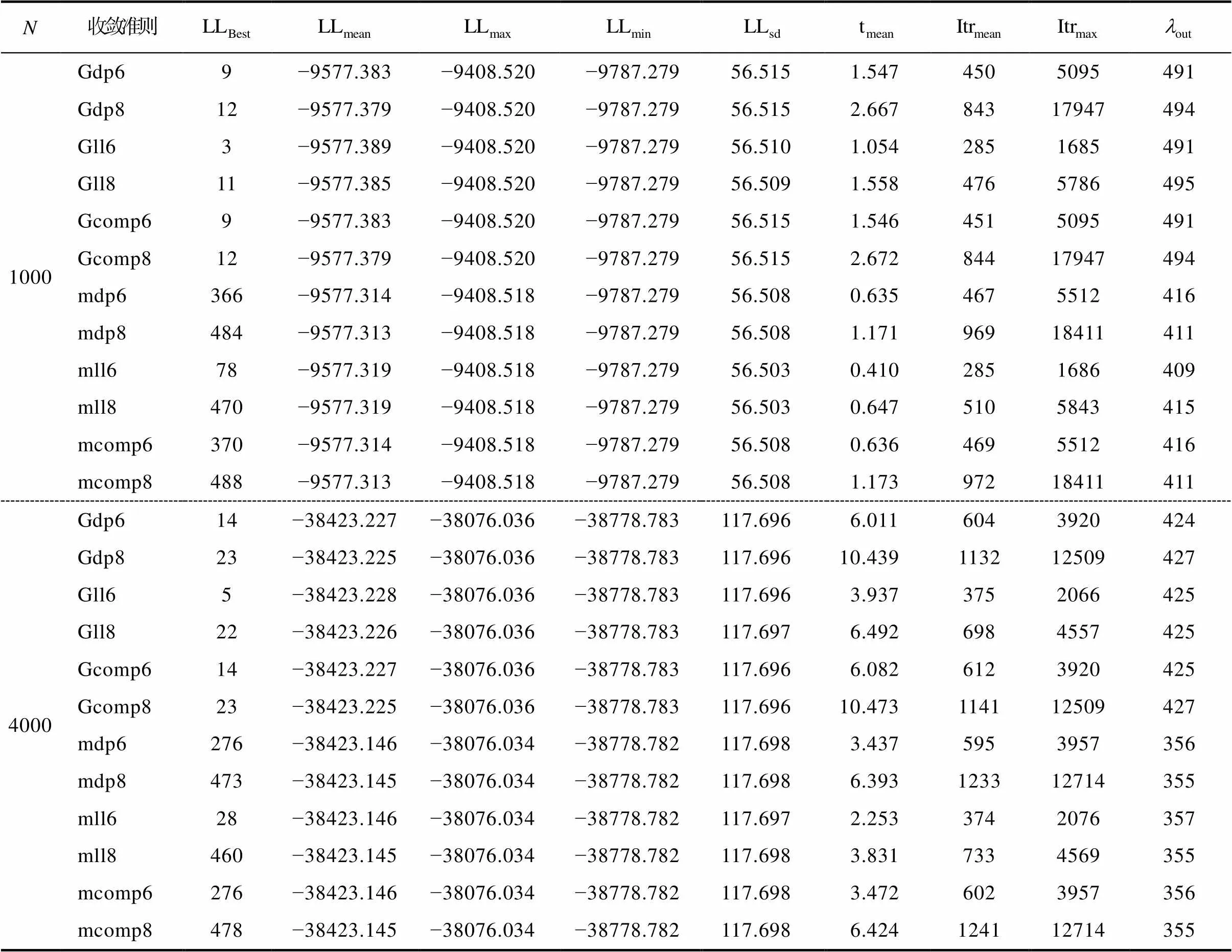
表5 HCDM生成数据, J = 16, N = 1000及4000条件下的模拟结果

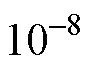
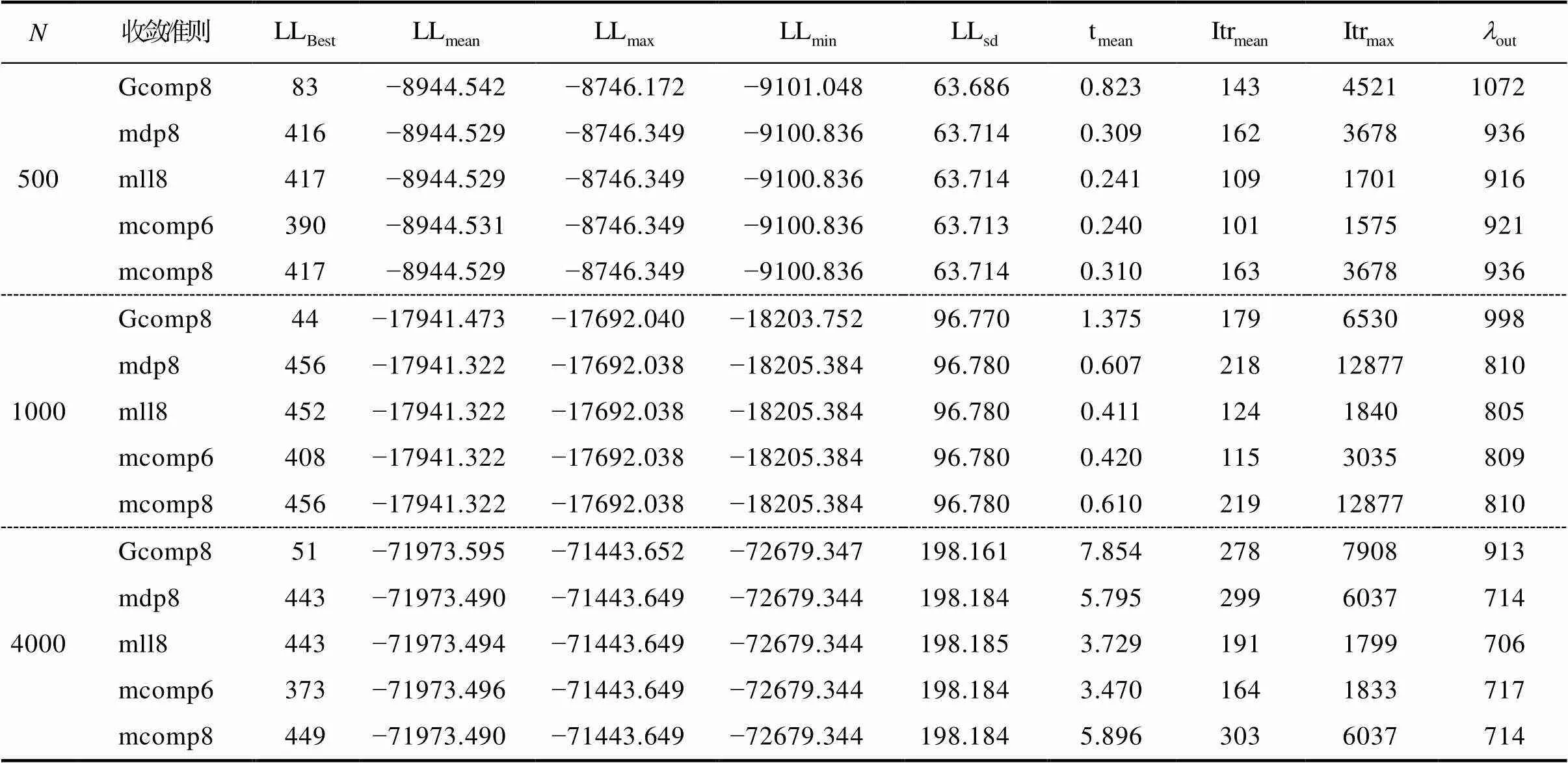
表6 HCDM生成数据, J = 32条件下的模拟结果

5 实证数据分析

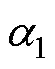
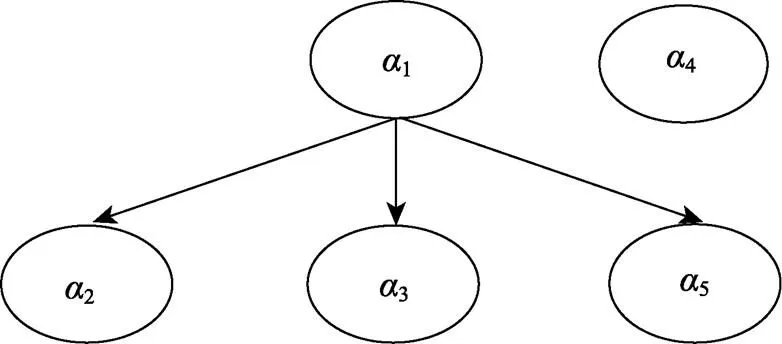
图4 Yuan等人(2022)定义的小学数学分数运算认知属性层级关系

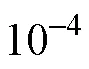
根据模型参数估计的极大似然理论, 收敛判断准则对应的LL越大, 说明这个准则的表现越好, 模型参数点估计值的可靠性越高。

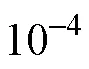
6 讨论与展望

本文通过理论分析及模拟研究证实, 心理计量模型的点估计值在一些情景中会存在可靠性问题, 且新开发的模型参数估计框架及收敛准则能够提高模型参数估计值的可靠性。

6.1 讨论

首先, 通过预研究作者认为最大迭代次数设置过少可能会导致模型参数不收敛的问题(如, 3000或以下, 见及软件包), 因此本研究将最大迭代次数设置为50000。模拟研究发现, 本文所有实验条件组合下和这两种模型参数估计框架均收敛。模拟研究显示在一些特定条件下(见表1),和的最大迭代次数均超过了30000次, 这也就意味着如果将最大收敛次数设置为3000那么就会出现模型参数不收敛的问题。因此, 本文认为增大模型参数估计程序的最大迭代次数有助于解决模型参数不收敛问题。

其次, 针对CDM中可能存在的边界值以及项目参数存在极端值问题, 本文开发了新的CDM模型参数估计框架。通过对比和这两种模型参数估计框架在模拟研究及实证数据分析中的表现, 发现框架的表现优于或至少与框架的表现相当; 且框架有效减少了项目参数极端值数量。因此, 本文认为在估计CDM模型参数时,可能是一个更好的选择。导致CDM中存在边界值的一个原因是属性间存在层级关系, 使得饱和CDM中的一些参数近似等于0。研究者以饱和CDM为基础开发了一些属性层级关系探索或验证的方法(Gu & Xu 2019; Liu et al., 2022; Templin & Bradshaw, 2014)。我们建议研究者进一步在框架下使用已有方法或者是开发新方法对属性层级关系进行研究。当有较为充分的证据证明层级关系存在时, 在框架下使用HCDM分析数据, 可能会提高模型参数点估计值的可靠性。

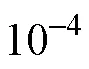
6.2 展望

本文以同一连接下的饱和G-DINA模型为例, 探讨了和框架下目前已有的及本研究新开发的各收敛准则在CDM模型参数估计中的表现。尽管本研究初步解决了在CDM模型参数估计时如何选择恰当收敛准则的问题, 但是作者认为有以下几个问题需要进一步探索。

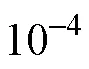
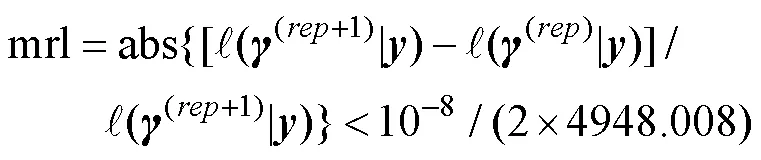
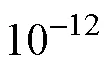
第二是关于框架及其应用的问题。本研究开发框架的主要目的在于提供一个更加合理的CDM模型参数估计框架, 尽量减少模型参数不收敛、边界值问题及项目参数极端值对CDM模型参数收敛准则表现的影响。特别说明的是模拟实验中将最大迭代次数设置为50000时, 两种参数估计框架下的所有循环中的参数估计都收敛了, 因此在本研究中框架仅在边界值问题及项目参数存在极端值时起作用。模型中存在边界值时, 尽管框架下的项目极端值数量少于同条件下框架所对应的数量, 但即使是在= 4000条件下,框架下出现极端值的频率仍然较高。因此, 本研究认为有必要以框架为基础, 继续对模型参数不收敛、边界值问题及项目参数极端值等问题展开探索。

第三, 不同连接函数下各种收敛准则的表现有待进一步探索。本文以同一连接下的饱和G-DINA模型为例, 探讨了不同收敛准则的表现。但CDM中还有两种得到广泛应用的连接：logit连接以及log连接(de la Torre, 2009, 2011; Templin & Bradshaw, 2014)。这3种连接函数的主要区别之一是, 项目参数与项目正确作答概率之间关系的表达不同。鉴于dp的表现在大多数情况下略优于ip, 本研究认为后续研究可以对不同连接函数下各个收敛准则的表现展开进一步探索。

American Psychological Association. (2020).(7th ed.). Washington.

Baker, M. (2016). 1,500 scientists lift the lid on reproducibility.(7604), 452−454.

Begley, C. G., & Ellis, L. M. (2012). Drug development: Raise standards for preclinical cancer research.(7391), 531−533.

Chiu, C. Y., Köhn, H. F., & Ma, W. (2023). Commentary on “Extending the Basic Local Independence Model to Polytomous Data” by Stefanutti, de Chiusole, Anselmi, and Spoto.(2), 656−671.

DeCarlo, T. (2011). On the analysis of fraction subtraction data: The DINA model, classification, latent class sizes, and the Q-Matrix.(1), 8−26.

DeCarlo, T. (2019). Insights from reparameterized DINA and beyond. In M. von Davier & Y.-S. Lee (Eds.).(pp. 549−572). Springer.

de la Torre, J. (2009). DINA model and parameter estimation: A didactic.(1), 115−130.

de la Torre, J. (2011). The generalized DINA model framework.(2), 179−199.

Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm.(1), 1−22.

Farrell, S., & Lewandowsky, S. (2018).. Cambridge University Press.

George, A. C., Robitzsch, A., Kiefer, T., Groß, J., & Ünlü, A. (2016). The R package CDM for cognitive diagnosis models.(2), 1−24.

Gu, Y., & Xu, G. (2019). Learning attribute patterns in high-dimensional structured latent attribute models.(115), 1−58.

Gu, Y., & Xu, G. (2020). Partial identifiability of restricted latent class models.(4), 2082− 2107.

Hu, C., Wang, F., Guo, J., Song, M., Sui, J., & Peng. K. (2014). The replication crisis in psychological research.,(9), 1504−1518.

[胡传鹏, 王非, 过继成思, 宋梦迪, 隋洁, 彭凯平. (2016). 心理学研究中的可重复性问题: 从危机到契机.(9), 1504−1518.]

Ioannidis, J. P. A. (2005). Why most published research findings are false.(8), e124.

Ioannidis, J. P. A. (2008). Why most discovered true associations are inflated.(5), 640−648.

Khorramdel, L., Shin, H. J., & von Davier, M. (2019). GDM softwareIncluding parallel EM algorithm. In M. von Davier & Y.-S. Lee (Eds.),(pp. 603−628). Springer.

Liu, R. (2018). Misspecification of attribute structure in diagnostic measurement.,(4), 605−634.

Liu, Y. (2022). Standard errors and confidence intervals for cognitive diagnostic models: Parallel bootstrap methods.(6), 703−724.

[刘彦楼. (2022). 认知诊断模型的标准误与置信区间估计：并行自助法.(6), 703−724.]

Liu, Y., Tian, W., & Xin, T. (2016). An application ofMstatistic to evaluate the fit of cognitive diagnostic models.(1), 3−26.

Liu, Y., Xin, T., & Jiang, Y. (2022). Structural parameter standard error estimation method in diagnostic classificationmodels: Estimation and application.,(5), 784−803.

Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses.(3), 253−275.

Ma, W., & de la Torre, J. (2020). GDINA: An R package for cognitive diagnosis modeling.(14), 1−26.

Ma, W., de la Torre, J., Sorrel, M., & Jiang, Z. (2022).. R package version 2.9.3. https://CRAN.R-project.org/package=GDINA

Ma, W., & Guo, W. (2019). Cognitive diagnosis models for multiple strategies.(2), 370−392.

Ma, W., & Jiang, Z. (2021). Estimating cognitive diagnosis models in small samples: Bayes modal estimation and monotonic constraints.,(2), 95−111.

Paek, I., & Cai, L. (2013). A comparison of item parameter standard error estimation procedures for unidimensional and multidimensional item response theory modeling.(1), 58−76.

Paulsen, J., & Valdivia, D. S. (2022). Examining cognitive diagnostic modeling in classroom assessment conditions.,(4), 916−933.

Philipp, M., Strobl, C., de la Torre, J., & Zeileis, A. (2018). On the estimation of standard errors in cognitive diagnosis models.(1), 88−115.

Robitzsch, A., Kiefer, T., George, A. C., & Uenlue, A. (2022).. R package version 8.2-6. http://CRAN.R-project.org/package=CDM

Rupp, A. A., Templin, J., & Henson, R. A. (2010).. Guilford Press.

Rupp, A. A., & van Rijn, P. W. (2018). GDINA and CDM packages in R.,(1), 71−77.

Sen, S., & Terzi, R. (2020). A comparison of software packages available for dina model estimation.,(2), 150−164.

Sorrel, M. A., Olea, J., Abad, F. J., de la Torre, J., Aguado, D., & Lievens, F. (2016). Validity and reliability of situational judgment test scores: A new approach based on cognitive diagnosis models.(3), 506−532.

Tajika, A., Ogawa, Y., Takeshima, N., Hayasaka, Y., & Furukawa, T. A. (2015). Replication and contradiction of highly cited research papers in psychiatry: 10-year follow-up.(4), 357−362.

Templin, J., & Bradshaw, L. (2014). Hierarchical diagnostic classification models: A family of models for estimating and testing attribute hierarchies.(2), 317−339.

Templin, J., & Hoffman, L. (2013). Obtaining diagnostic classification model estimates using.(2), 37−50.

Tian, W., Xin, T., & Kang, C. (2014). The data-augmentation techniques in item response modeling: Current approaches and new developments.,(6), 1036−1046.

[田伟, 辛涛, 康春花. (2014). 项目反应理论中潜在心理特质“填补”的参数估计方法及其演变.,(6), 1036−1046.]

von Davier, M. (2008). A general diagnostic model applied to language testing data.,(2), 287−307.

Wu, Z., Deloria-Knoll, M., & Zeger, S. L. (2017). Nested partially latent class models for dependent binary data; estimating disease etiology.(2), 200−213.

Xu, X., & von Davier, M. (2008). Fitting the structured general diagnostic model to NAEP data.,(1), i−18.

Yamaguchi, K. (2023). On the boundary problems in diagnostic classification models.(1), 399−429.

Yuan, L., Liu, Y., Chen, P., & Xin, T. (2022). Development of a new learning progression verification method based on the hierarchical diagnostic classification model: Taking grade 5 students’ fractional operations as an example.(3), 69−82.

Zeng, Z., Gu, Y., & Xu, G. (2023). A Tensor-EM method for large-scale latent class analysis with binary responses.(2), 580−612.

On the reliability of point estimation of model parameters:Taking cognitive diagnostic models as an example

LIU Yanlou1,2, CHEN Qishan3,4, WANG Yiming2, JIANG Xiaotong2

(1Academy of Big Data for Education;2School of Psychology, Qufu Normal University, Jining 273165, China) (3Philosophy and Social Science Laboratory of Reading and Development in Children and Adolescents (South China Normal University), Ministry of Education;4School of Psychology, South China Normal University, Guangzhou 510631, China)

Cognitive diagnostic models (CDMs) are psychometric models that have received increasing attention within fields such as psychology, education, sociology, and biology. It has been argued that an inappropriate convergence criterion for a maximum likelihood estimation using the expectation maximization (MLE-EM) algorithm could result in unpredictable and inaccurate model parameter estimates. Thus, inappropriate convergence criteria may yield unstable and misleading conclusions from the fitted CDMs. Although several convergence criteria have been developed, it remains an unexplored question, how to specify the appropriate convergence criterion for fitted CDMs.

A comprehensive method for assessing convergence is proposed in this study. To minimize the influence of the model parameter estimation framework, a new framework adopting the multiple starting values strategy () is introduced. To examine the performance of the convergence criterion for MLE-EM in CDMs, a simulation study under various conditions was conducted. Five convergence assessment methods were examined: the maximum absolute change in model parameters, the maximum absolute change in item endorsement probabilities and structural parameters, the absolute change in log-likelihood, the relative log-likelihood, and the comprehensive method. The data generating models were the saturated CDM and the hierarchical CDM. The number of items was set to= 16 and 32. Three levels of sample sizes were considered: 500, 1000, and 4000. The three convergence tolerance value conditions were 10–4, 10–6, and 10–8. The simulated response data were fitted by the saturated CDM using theand the R package. The maximum number of iterations was set to 50000.

The simulation results suggest the following.

(1) The saturated CDM converged under all conditions. However, the actual number of iterations exceeded 30000 under some conditions, implying that when the predefined maximum iteration number is less than 30000, the MLE-EM algorithm might inadvertently stop.

(2) The model parameter estimation framework affected the performance of the convergence criteria. The performance of the convergence criteria under theframework was comparable or superior to that of theframework.

(3) Regarding the convergence tolerance values considered in this study, 10–8consistently had the best performance in providing the maximum value of the log-likelihood and 10–4had the worst performance. Compared to all other convergence assessment methods, the comprehensive method in general had the best performance, especially under theframework. The performance of the maximum absolute change in model parameters was similar to the comprehensive method, but this good performance was not consistent. On the contrary, the relative log-likelihood had the worst performance under theandframeworks.

The simulation results showed that the most appropriate convergence criterion for MLE-EM in CDMs was the comprehensive method with tolerance 10–8under theframework. The results from the real data analysis also demonstrated that the proposed comprehensive method andframework had good performance.

model parameter estimation, point estimation, convergence criterion, cognitive diagnostic model

B841

https://doi.org/10.3724/SP.J.1041.2023.01712

2023-03-02

*国家自然科学基金青年项目(31900794)、山东省教育科学规划课题(2020KZD009)、广东省哲学社会科学规划项目(GD22CXL01)、广东省教育科学规划课题(2022GXJK176)和大学生创新创业训练计划(202110446231X)资助。

刘彦楼, E-mail: liuyanlou@163.com