限制李三系的型心
2023-10-09刘艳培董艳芹周涵琪
刘艳培, 董艳芹, 周涵琪, 丛 昕
(长春师范大学 数学学院, 吉林 长春 130032)
1 基本概念
李三系理论已经有了很好的发展, 文献[1]给出了李三系的广义导子和拟导子, 并对其进行研究.随着李三系的发展, 限制李三系也有了一定的发展[2-6]. 本文总设基域F的特征为p, 其中p为大于2的素数.设T为域F上的向量空间, 若T上有三元线性运算[·, ·, ·], 满足下面三个条件:
[x,y,z]=-[y,x,z];
[x,y,z]+[y,z,x]+[z,x,y]=0;
[u,v, [x,y,z]]=[[u,v,x],y,z]+[x,[u,v,y],z]+[x,y, [u,v,z]], ∀x,y,z,u,v∈T, 称T为李三系.设T是一个李三系, ∀x,y∈T.定义
L(x,y)∈End(T),L(x,y)z=[x,y,z];
用L(T,T)表示由L(x,y)线性张成的空间.定义Ls(T)=L(T,T)⊕T, 其中Ls(T)上的运算为:
[X1,X2]=([H1,H2]+L(x1,x2))⊕H1x2-H2x1,
其中Xi=xi+HiHi∈L(T,T),xi∈T(i=1, 2).
定义1.1[4]设T为域F上的李三系, 如果存在一个映射[p]:T→T, 对于∀a,b,c∈T,α∈F满足下面条件:
(αa)[p]=αpa[p]
[a,b[p],c]=(a,b, …,b,c)(p个b),
其中isi(a,b)是λi-1在(ad(λa+b))p-1(a)∈Ls(T)中的系数, 则称(T, [p])为限制李三系.通常简称T为限制李三系.在这里,
(a,b, …,b,c)=[[[[a,b,b],b,b], …],b,c].
引理1.1设T为域F上的限制李三系, End(T)为T的所有线性变换构成的集合.令[p]:D→Dp, ∀D∈End(T), 则End(T)为限制李三系.
证明:∀D,D1,D2∈End(T),α∈F, 有(αD)p=(αD)(αD)…(αD)=αpDp.显然有
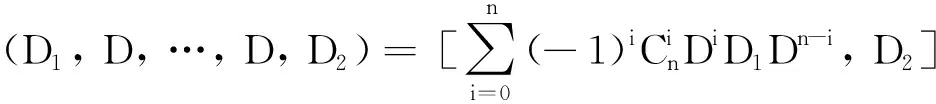
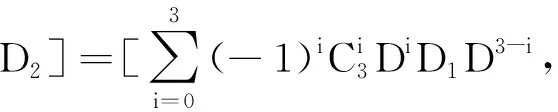
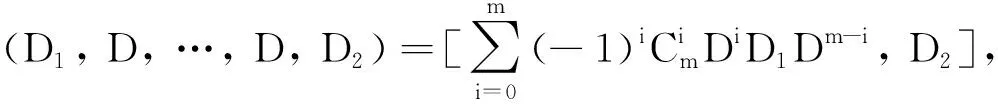
结论成立.特别地, 取n=p, 则

因此End(T)为限制李三系.
限制李三系T的一个子空间ψ, 如果满足[ψ,ψ,ψ]⊆ψ, 且对于∀x∈ψ,x[p]∈ψ, 则称ψ为T的一个p-子系.
限制李三系T的一个子空间φ, 如果满足[φ,T,T]⊆φ, 且对于∀x∈φ,x[p]∈φ, 则称φ为T的一个p-理想.
定义1.2设T为域F上的限制李三系.如果
C(T)={D∈End(T)|[D(x),y,z]=[x,D(y),z]=[x,y,D(z)]=D([x,y,z])}, ∀x,y,z∈T, 那么C(T)被称为T的型心.
定义1.3设T为域F上的限制李三系.如果
QC(T)={D∈End(T)|[D(x),y,z]=[x,D(y),z]=[x,y,D(z)]}, ∀x,y,z∈T,
那么QC(T)被称为T的拟型心.
定义1.4设T为域F上的限制李三系,I是T的非空子集.我们定义I在T的中心
ZT(I)={x∈T∣[x,a,y]=[y,a,x]=0, ∀a∈I,y∈T}.
特别地,T的中心为Z(T)=ZT(T)={x∈T∣[x,y,z]=0, ∀y,z∈T}.
2 型心及拟型心的结构性质
定理2.1设T为域F上的限制李三系, 则C(T)为End(T)的p-子系.
证明:假设D,D1,D2,D3∈C(T), ∀x,y,z∈T,p∈F.由
[[D1,D2]D3(x),y,z]=[D1D2D3(x),y,z]-[D2D1D3(x),y,z]=[D2D3(x),D1(y),z]-[D1D3(x),D2(y),z]=[D3(x),D2D1(y),z]-[D3(x),D1D2(y),z]=[D3(x), [D2,D1](y),z]=-[x,D3[D1,D2](y),z][D3[D1,D2](x),y,z]=[D1D2(x),D3(y),z]-[D2D1(x),D3(y),z]=
[D2(x),D1(D3(y)),z]-[D1(x),D2(D3(y)),z]=[x,D2D1(D3(y)),z]-[x,D1D2(D3(y)),z] =[x, [D2,D1](D3(y)),z]=-[x, [D1,D2](D3(y)),z],
得到
[[D1,D2,D3](x),y,z]=[[D1,D2]D3(x),y,z]-[D3[D1,D2](x),y,z]=-[x,D3[D1,D2](y),z]-(-[x, [D1,D2](D3(y)),z]) =[x, [D1,D2,D3](y),z].
类似可证[[D1,D2,D3](x),y,z]=[x,y, [D1,D2,D3](z)]=[D1,D2,D3]([x,y,z]).所以C(T)为End(T)的子系.
又因为
[D[p](x),y,z]=[Dp(x),y,z]=[DDp-1(x),y,z]=[Dp-1(x),D(y),z]=[DDp-2(x),D(y),z]=[Dp-2(x),D2(y),z]=…=[x,Dp(y),z]=[x,D[p](y),z].
同理, [D[p](x),y,z]=[x,y,D[p](z)]=D[p]([x,y,z]).因此D[p]∈C(T),C(T)为End(T)的p-子系.
命题2.2设T为域F上的限制李三系, 则QC(T)为End(T)的p-子系.
证明:假设D,D1,D2,D3∈QC(T), ∀x,y,z∈T,p∈F.由
[[D1,D2]D3(x),y,z]=[D1D2D3(x),y,z]-[D2D1D3(x),y,z]=[D2D3(x),D1(y),z]-[D1D3(x),D2(y),z]=[D3(x),D2D1(y),z]-[D3(x),D1D2(y),z]=[D3(x), [D2,D1](y),z]=-[x,D3[D1,D2](y),z],
[D3[D1,D2](x),y,z]=[D1D2(x),D3(y),z]-[D2D1(x),D3(y),z]=[D2(x),D1(D3(y)),z]-[D1(x),D2(D3(y)),z]=[x,D2D1(D3(y)),z]-[x,D1D2(D3(y)),z] =[x, [D2,D1](D3(y)),z]=-[x, [D1,D2](D3(y)),z],
得到
[[D1,D2,D3](x),y,z]=[[D1,D2]D3(x),y,z]-[D3[D1,D2](x),y,z]=-[x,D3[D1,D2](y),z]-(-[x, [D1,D2](D3(y)),z]) =[x, [D1,D2,D3](y),z].
类似可证[[D1,D2,D3](x),y,z]=[x,y, [D1,D2,D3](z)].所以QC(T)为End(T)的子系.
又因为
[D[p](x),y,z]=[Dp(x),y,z]=[DDp-1(x),y,z]=[Dp-1(x),D(y),z]=[DDp-2(x),D(y),z]=[Dp-2(x),D2(y),z]=…=[x,Dp(y),z]=[x,D[p](y),z].
同理, [D[p](x),y,z]=[x,y,D[p](z)].因此D[p]∈QC(T),QC(T)为End(T)的p-子系.
定理2.3设T为域F上的限制李三系, 如果T可分解为两个p-理想A,B的直和, 即T=A⊕B, 并且Z(T)=0, 那么C(T)=C(A)⊕C(B).
证明:∀D∈C(A),D(x1+x2)=D(x1), ∀x1∈A,x2∈B延拓到T上, 显然D∈C(T),C(A)⊆C(T).
同理,C(B)⊆C(T).易知:D∈C(A)当且仅当D(x2)=0, ∀x2∈B;D∈C(B)当且仅当D(x1)=0, ∀x1∈A.因此C(A)⊕C(B)⊆C(T),C(A)∩C(B)=0.
∀D∈C(T), ∀x1∈A,x2,x3∈B, [D(x1),x2,x3]=[x1,D(x2),x3]∈A∩B={0}.因为Z(T)=0, 且Z(T)=Z(A)⊕Z(B), 所以D(x1)∈A, ∀x1∈A.同理,D(x2)∈B, ∀x2∈B.∀D1∈C(A), ∀D∈C(T), ∀x2∈B, 则[D,D1](x2)=DD1(x2)-D1D(x2)=0.
所以[D,D1]∈C(A),C(A)为C(T)的理想.∀D∈C(A), ∀x1,x2,x3∈A,
[D[p](x1),x2,x3]=[Dp(x1),x2,x3]=[Dp-1(x1),D(x2),x3]=…=[x1,Dp(x2),x3]=[x1,D[p](x2),x3].
同理, [D[p](x1),x2,x3]=[x1,x2,D[p](x3)]=D[p]([x1,x2,x3]), 则C(A)为C(T)的p-理想.同理,C(B)为C(T)的p-理想.
∀D∈C(T), 取x=x1+x2, ∀x1∈A,x2∈B, 令D1(x1+x2)=D(x1),D2(x1+x2)=D(x2), 则D2∈C(B),D2∈C(B).又D=D1+D2, 所以D∈C(A)+C(B),C(T)⊆C(A)+C(B).因此C(T)=C(A)⊕C(B).
命题2.4设T为域F上的限制李三系, 如果T可分解为两个p-理想A,B的直和, 即T=A⊕B, 并且Z(T)=0, 那么QC(T)=QC(A)⊕QC(B).
证明:∀D∈QC(A),D(x1+x2)=D(x1), ∀x1∈A,x2∈B延拓到T上, 显然D∈QC(T),QC(A)⊆QC(T).同理,QC(B)⊆QC(T).易知:D∈QC(A)当且仅当D(x2)=0, ∀x2∈B;D∈QC(B)当且仅当D(x1)=0, ∀x1∈A.因此QC(A)⊕QC(B)⊆QC(T),QC(A)∩QC(B)=0.
∀D∈QC(T), ∀x1∈A,x2,x3∈B, [D(x1),x2,x3]=[x1,D(x2),x3]∈A∩B={0}.因为Z(T)=0, 且Z(T)=Z(A)⊕Z(B), 所以D(x1)∈A, ∀x1∈A.同理,D(x2)∈B, ∀x2∈B.∀D1∈QC(A), ∀D∈QC(T), ∀x2∈B, 则[D,D1](x2)=DD1(x2)-D1D(x2)=0,
所以[D,D1]∈QC(A),QC(A)为QC(T)的理想.∀D∈QC(A), ∀x1,x2,x3∈A,
[D[p](x1),x2,x3]=[Dp(x1),x2,x3]=[Dp-1(x1),D(x2),x3]=…=[x1,Dp(x2),x3] =[x1,D[p](x2),x3]
同理, [D[p](x1),x2,x3]=[x1,x2,D[p](x3)], 则QC(A)为QC(T)的p-理想.同理,QC(B)为QC(T)的p-理想.
∀D∈QC(T), 取x=x1+x2, ∀x1∈A,x2∈B, 令D1(x1+x2)=D(x1),D2(x1+x2)=D(x2), 则D1∈QC(A),D2∈QC(B).又D=D1+D2, 所以D∈QC(A)+QC(B),QC(T)⊆QC(A)+QC(B).因此QC(T)=QC(A)⊕QC(B).
命题2.5设T为域F上的限制李三系, 且Z(T)=0, 若D∈C(T), 则Ker(D)是T的p-理想.
证明:∀x∈Ker(D), ∀y,z∈T.因为x∈Ker(D), 所以D(x)=0.又D∈C(T),
D([x,y,z])=[D(x),y,z]=0,
所以[x,y,z]∈Ker(D),Ker(D)为T的理想.又
D([x[p],y,z])=-D([y,x[p],z])=-D(y,x,x, …,z)=-D([[[[y,x,x],x,x], …],x,z])=-([[[[y,x,x],x,x], …],D(x),z])=0,
D([x[p],y,z])=[D(x[p]),y,z])=0.又Z(T)=0, 则D(x[p])=0,x[p]∈Ker(D).Ker(D)是T的p-理想.
命题2.6设T为域F上的限制李三系, 且Z(T)=0, 若D∈C(T), 则Im(D)是T的p-理想.
证明:∀x∈Im(D), ∀y,z∈T.因为x∈Im(D), 那么∃x′∈T, 使得D(x′)=x.又D∈C(T), [x,y,z]=[D(x′),y,z]=D([x′,y,z]), 所以[x,y,z]∈Im(D),Im(D)是T的理想.而
[x[p],y,z]=-[y,x[p],z]=-(y,x,x, …,z)=-[[[[y,x,x],x,x], …],x,z]=-[[[[y,x,x],x,x], …],D(x′),z]=-D([[[[y,x,x],x,x], …],x′,z])=-Dp([[[[y,x′,x′],x′,x′], …],x′,z])=Dp[x′[p],y,z]=[D(Dp-1(x′[p])),y,z].
又Z(T)=0,x[p]=D(Dp-1(x′[p]))∈Im(D).因此Im(D)是T的p-理想.
